Файл: Уравнения и неравенства с двумя переменными.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 29.10.2023

Просмотров: 1042

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


S30 =   · 30;  S30 =   · 30 = 1605.

S14 =   · 14;  S14 =   · 14 = 413.

S30 – S14 = 1192.

О т в е т: 1192.

№ 612.

(сп) – арифметическая прогрессия;

с7 = 18,5; с17 = –26,5.





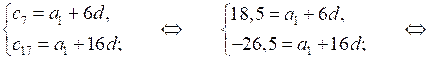
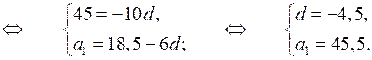
S20 =   · 20;  S20 =   · 20 = 55.

О т в е т: 55.

№ 616.

Количество шаров в каждом ряду можно представить в виде арифметической прогрессии (ап), где а1 = 1; d = 1.

1. Sn = 120. Найти п.

Sn =   · п;  120 =   · п;

240 = (п + 1) · п;

п2 + п – 240 = 0;

п = 15 или п = –16, так как п  N, то выбираем п = 15.

2. п = 30. Найти S30.

S30 =   · 30;  S30 =   · 30 = 465.

О т в е т: 15 рядов, 465 шаров.

V. Итоги урока.

Ответить на контрольные вопросы (учебник, с. 153).

Домашнее задание: № 609 (б; г), № 611, № 613

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

У р о к  64                                                              Дата:
КОНТРОЛЬНАЯ РАБОТА № 4

В а р и а н т  1

1. Найдите двадцать третий член арифметической прогрессии (ап), если а1 = –15 и d = 3.

2. Найдите сумму шестнадцати первых членов арифметической прогрессии: 8; 4; 0; …

3. Найдите сумму шестидесяти первых членов последовательности (bп), заданной формулой b
п = 3п – 1.

4. Является ли число 54,5 членом арифметической прогрессии (ап), в которой а1 = 25,5 и а9 = 5,5?

5. Найдите сумму всех натуральных чисел, кратных 3 и не превосходящих 100.

В а р и а н т  2

1. Найдите восемнадцатый член арифметической прогрессии (ап), если а1 = 70 и d = –3.

2. Найдите сумму двадцати первых членов арифметической прогрессии: –21; –18; –15; …

3. Найдите сумму сорока первых членов последовательности (bп), заданной формулой bп = 4п – 2.

4. Является ли число 30,4 членом арифметической прогрессии (ап), в которой а1 = 11,6 и а15 = 17,2?

5. Найдите сумму всех натуральных чисел, кратных 7 и не превосходящих 150.

В а р и а н т  3

1. Найдите тридцать второй член арифметической прогрессии (ап), если а1 = 65 и d = –2.

2. Найдите сумму двадцати четырех первых членов арифметической прогрессии: 42; 34; 26; …

3. Найдите  сумму  восьмидесяти  первых  членов  последовательности (bп), заданной формулой bп = 2п – 5.

4. Является ли число 6,5 членом арифметической прогрессии (ап), в которой а1 = –2,25 и а11 = 10,25?

5. Найдите сумму всех натуральных чисел, кратных 9 и не превосходящих 80.

В а р и а н т  4

1. Найдите  сорок  третий  член  арифметической прогрессии (ап), если а1 = –9 и d = 4.

2. Найдите сумму четырнадцати первых членов арифметической прогрессии: –63; –58; –53; …

3. Найдите сумму ста двадцати первых членов последовательности (bп), заданной формулой bп = 3п – 2.

4. Является ли число 35,8 членом арифметической прогрессии (ап), в которой а1 = –23,6 и а22 = 11?

5. Найдите сумму всех натуральных чисел, кратных 6 и не превосходящих 150.

В контрольной работе задания 1 и 2 обязательного уровня.

РЕШЕНИЕ ВАРИАНТОВ КОНТРОЛЬНОЙ РАБОТЫ

В а р и а н т  1

1. (ап) – арифметическая прогрессия; а1 = –15, d = 3.

а23 = а1 + 22d; а23
 = –15 + 22 · 3 = –15 + 66 = 51.

О т в е т: 51.

2. 8; 4; 0; … – арифметическая прогрессия;

а1 = 8, d = – 4.

Sn =   · п;  S16 =   · 16 = (16 – 60) · 8 =
= –44 · 8 = –352.

О т в е т: –352.

3. bп = 3п – 1, значит, (bп) – арифметическая прогрессия.

b1 = 3 · 1 – 1 = 2; b60 = 3 · 60 – 1 = 179;

Sn = 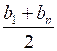  · п;  S60 =   · 60 = 181 · 30 = 5430.

О т в е т: 5430.

4. (ап) – арифметическая прогрессия; а1 = 25,5; а9 = 5,5.

Пусть ап = 54,5.

d =  ;  d =   =   = –2,5;

ап = а1 + d (п – 1);   54,5 = 25,5 – 2,5 (п – 1);   2,5 (п – 1) = –29;

п – 1 = –11,6;   п = –10,6, п  N, значит, 54,5 не является членом арифметической прогрессии (ап).

О т в е т: нет.

5. (ап) – арифметическая прогрессия; ап = 3п; ап ≤ 100;

3п ≤ 100; п ≤ 33 , так как п  N,то п = 33.

Sn =   · п; а1 = 3; а33 = 99, тогда

S33 =   · 33 = 1683.

О т в е т: 1683.

В а р и а н т  2

1. (ап) – арифметическая прогрессия; а1 = 70, d = –3.

а18 = а1 + 17d; а18 = 70 + 17 · (–3) = 70 – 51 = 19.

О т в е т: 19.

2. –21; –18; –15; … – арифметическая прогрессия;

а1 = –21, d = 3.

Sn =   · п;  S20 =   · 20 =   · 20 =
= 15 · 10 = 150.

О т в е т: 150.

3. bп = 4п – 2, значит, (bп) – арифметическая прогрессия.

b1 = 2; b40 = 4 · 40 – 2 = 160 – 2 = 158;

Sn = 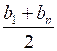  · п;  S40 =   · 40 = 160 · 20 = 3200.

О т в е т: 3200.

4. (ап) – арифметическая прогрессия; а1 = 11,6; а15 = 17,2.

Пусть ап = 30,4.

d = 
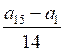
;  d =   =   = 0,4;

ап = а1 + d (п – 1);   30,4 = 11,6 + 0,4 (п – 1);   0,4 (п – 1) = 18,8;

п – 1 = 47;   п = 48, п  N, значит, 30,4 является членом арифметической прогрессии (ап).

О т в е т: да.

5. (ап) – арифметическая прогрессия; ап = 7п; ап ≤ 150;

7п ≤ 150; п ≤ 21 , так как п  N,то п = 21.

Sn =   · п; а1 = 7; а21 = 147, тогда

S21 =   · 21 = 77 · 21 = 1617.

О т в е т: 1617.

В а р и а н т  3

1. (ап) – арифметическая прогрессия; а1 = 65, d = –2.

а32 = а1 + 31d; а32 = 65 + 31 · (–2) = 65 – 62 = 3.

О т в е т: 3.

2. 42; 34; 26; … – арифметическая прогрессия;

а1 = 42, d = –8.

Sn =   · п;  S24 =   · 24 =   · 24 =
= –100 · 12 = –1200.

О т в е т: –1200.

3. bп = 2п – 5, значит (bп) – арифметическая прогрессия.

b1 = –3; b80 = 2 · 80 – 5 = 160 – 5 = 155

Sn =   · п;  S30 =   · 80 = 152 · 40 = 6080.

О т в е т: 6080.

4. (ап) – арифметическая прогрессия; а1 = –2,25; а11 = 10,25.

Пусть ап = 6,5.

d =  ;  d =   = 1,25.

ап = а1 + d (п – 1);   6,5 = –2,25 + 1,25 (п – 1);

1,25 (п – 1) = 8,75;

п – 1 = 7;   п = 8, п  N, значит, число 6,5 является членом арифметической прогрессии (ап).

О т в е т: да.

5. (ап) – арифметическая прогрессия, ап = 9п; ап ≤ 80;

9п ≤ 80; п ≤ 8 , так как п  N,то п = 8.

а1 = 9; а8 = 72, Sn =   · п;  S8 =   · 8 = 324.

О т в е т: 324.

В а р и а н т  4

1. (ап) – арифметическая прогрессия; а1 = –9, d = 4.

а43 = а1 + 42d; а43 = –9 + 42 · 4 = –9 + 168 = 159.

О т в е т: 159.

2. –63; –58; –53; … – арифметическая прогрессия;

а1 = –63, d = 5.

Sn =   · п;  S14 =   · 14 =   · 14 =
= –61 · 7 = –427.

О т в е т: –427.

3. bп = 3п – 2, значит (bп) – арифметическая прогрессия.

b1 = 1; b120 = 3 · 120 – 2 = 358

Sn =   · п;  S120 =   · 120 = 359 · 60 = 21540

О т в е т: 21540.

4. (ап) – арифметическая прогрессия, а1 = –23,6; а22 = 11.

Пусть ап = 35,8.

d =  ;  d =   =   = 1 ;

ап = а1 + d (п – 1);   35,8 = –23,6 +  (п – 1);

(п – 1) = –59,4; п – 1 =  ;   п – 1 = 36 ;

п = 37 , п  N, значит, число 35,8 не является членом арифметической прогрессии (ап).

О т в е т: нет.

5. (ап) – арифметическая прогрессия; ап = 6п; ап ≤ 150;

6п ≤ 150; п ≤ 25, так как п  N, то п = 25.

Sn =   · п;  ; а1 = 6; а25 = 150, тогда

S25 =   · 25 = 78 · 25 = 1950.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

У р о к  65                                                              Дата:

Смотрите также файлы