ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ. ФОРМУЛА
п-го ЧЛЕНА ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ

Цели: ввести понятия геометрической прогрессии и знаменателя геометрической прогрессии; вывести формулу п-го члена геометрической прогрессии; формировать умения нахождения знаменателя и нескольких первых членов геометрической прогрессии по первому члену и знаменателю, а также п-го члена по формуле.

Ход урока

I. Организационный момент.

II. Анализ результатов контрольной работы.

Разбор типичных ошибок, допущенных учащимися в контрольной работе, консультация учителя.

III. Устная работа.

Подставьте в квадратик пропущенный элемент, назовите формулу для арифметической прогрессии (а_п).

а) а_{п + 1} = а₁ + o;

б) а_п = а₁ + d · o;

в) 2а_п = o + а_{п + 1};

г) o = kn + b;

д)  ;

е)  .

IV. Объяснение нового материала.

1. Для мотивации изучения геометрической прогрессии целесообразно начать с решения задачи практического характера, например по расчету банковских процентов.

З а д а ч а. Родители девятиклассника положили на его имя в банк 10000 рублей на счет, по которому сумма вклада ежегодно возрастает на 9 %. Какая сумма будет на счету к его совершеннолетию через три года? Через шесть лет?

Р е ш е н и е

Начальная сумма вклада составляет 10000 р. Через год эта сумма возрастает на 9 % и составит 109 % от 10000 р. Обозначим b₁ сумму на счету к концу первого года, тогда b₁ = 10000 · 1,09 (р.). К концу второго года уже сумма b₁ увеличится на 9 % и составит b₂ = b₁ · 1,09. К концу третьего года сумма составит b₃ = b₂ · 1,09. И так далее.

Рассмотрим последовательность b₁, b₂, b₃, … b₆, … b_п, в ней каждый член, начиная со второго, получен умножением предыдущего члена на 1,09. Эта последовательность является примером геометрической прогрессии.

---

2. Определение. Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.

(b_п) – геометрическая прогрессия, если для любого n  N выполняются условия b_п ≠ 0 и b_{п + 1} = b_п · q, где q – некоторое число. Число q называется знаменателем геометрической прогрессии, так как из определения следует, что   = q.

Напоминаем ученикам, что геометрическая прогрессия – частный вид последовательности, заданной рекуррентным способом.

3. Характер поведения геометрической прогрессии в зависимости от значений q следует разобрать с учащимися более детально, например по такому плану:

а) Пусть q > 1, тогда члены геометрической прогрессии таковы, что их значения имеют один и тот же знак и возрастают по модулю.

П р и м е р: 1; 3; 9; 27; 81; … (то есть b₁ = 1, q = 3) или

–2; –8; –32; … (то есть b₁ = –2, q = 4).

б) Если 0 < q < 1, то члены геометрической прогрессии таковы, что их значения имеют один и тот же знак и убывают по модулю.

П р и м е р:   (то есть b₁ = 1, q =  ) или

 (то есть b₁ = –1, q =  ).

в) Пусть q < –1, тогда члены геометрической прогрессии принимают знакочередующиеся значения, убывающие по модулю.

П р и м е р:   (то есть b₁ = –8, q =  ).

д) При q = 1 все члены геометрической прогрессии одинаковы, то есть b₁; b₁; b₁; …; b₁; …, а при q = –1 все члены геометрической прогрессии отличаются друг от друга лишь знаками, то есть: а₁; –а₁; а₁; –а₁; …

4. Вывод формулы п-го члена не вызывает затруднений у учащихся, действуем по аналогии с арифметической прогрессией. Сильному в учебе классу можно предложить провести доказательство самостоятельно.

---

 Пусть (b_п) – геометрическая прогрессия и b₁ – первый член, q – знаменатель, тогда

b₂ = b₁ · q

b₃ = b₂ · q = (b₁ · q) · q = b₁ · q²

b₄ = b₃ · q = (b₁ · q²) · q = b₁ · q³

b₅ = b₄ · q = (b₁ · q³) · q = b₁ · q⁴

… …

 – формула п-го члена геометрической прогрессии 

V. Формирование умений и навыков.

1. Вернемся к решению задачи с банковскими процентами. Мы имеем геометрическую прогрессию (b_п), где b₁ = 10000, q = 1,09. Сумма, накопленная вкладчиком, через три года будет равняться четвертому члену этой прогрессии, а через шесть лет – седьмому.

В ы ч и с л и м:         b₄ = 10000 · (1,09)³ ≈ 12950;

                                 b₇ = 10000 · (1,09)⁶ ≈ 16771.

О т в е т: на счету у вкладчика через три года окажется сумма, приближенно равная 12950 р.; через шесть лет – 16771 р.

2. Упражнения:

№ 623 (а, в), № 624 (а, в, д). Самостоятельное решение с последующей проверкой.

№ 627 (а, б), № 628 (б, в). Решение у доски с объяснениями.

VI. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Сформулируйте определение геометрической прогрессии.

– Сформулируйте определение знаменателя геометрической прогрессии.

– Назовите формулу п-го члена геометрической прогрессии.

Домашнее задание: № 623 (б, г), № 624 (б, г, е), № 627 (в, г), № 628 (а, г),

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

У р о к  66                                                                              Дата:
СВОЙСТВО ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ

Цели: вывести и доказать характеристическое свойство геометрической прогрессии; формировать умение применять свойство геометрической прогрессии при решении задач; закрепить умения и навыки применения определения и формулы 

---

п-го члена геометрической прогрессии.

Ход урока

I. Организационный момент.

II. Математический диктант.

Работа выполняется по вариантам (в квадратных скобках дано задание, относящееся ко второму варианту).

1) У геометрической прогрессии первый член 8 [9], второй член 4 [3]. Найдите знаменатель q.

2) У геометрической прогрессии первый член 9 [8], второй член 3 [4]. Найдите третий член.

3) Найдите четвертый [шестой] член геометрической прогрессии, если ее первый член равен 1, а знаменатель q равен –2.

4) Является ли последовательность степеней числа 2 [3] геометрической прогрессией?

5) Является ли последовательность четных [нечетных] чисел геометрической прогрессией?

О т в е т ы:           1) 

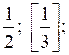
                              2) 1 [2];

                              3) –8 [–32];

                              4) да [да];

                              5) нет [нет].

III. Объяснение нового материала.

1. Создание проблемной ситуации, востребование умения действовать «по аналогии».

Арифметическая прогрессия (ап)		Геометрическая прогрессия (bn)
an – 1 = an – d		bn – 1 =
an		bn
an + 1 = an + d		bn + 1 = bn · q
an – 1 + an + 1 = an – d + an + d an – 1 + an + 1 = 2an	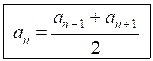	bn – 1 · bn + 1 =   · bn · q bn – 1 · bn + 1 =

---

Здесь следует обратить внимание учащихся, что при выводе соответствующего свойства для арифметической прогрессии в равенствах у нас были слагаемые d и – d, поэтому для их сокращения требовалось почленно складывать неравенства. Для геометрической прогрессии в равенствах сомножители q и  , поэтому следует перемножить равенства.

2. Теперь можно сформулировать  с в о й с т в о  геометрической прогрессии: «Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению предыдущего и последующего ее членов».

 Доказательство приведено выше. 

Как и в случае с арифметической прогрессией, можно доказать обратную теорему, которая будет являться  п р и з н а к о м  геометрической прогрессии: «Если в последовательности чисел, отличных от нуля, квадрат каждого члена, начиная со второго, равен произведению предыдущего и последующего членов, то эта последовательность является геометрической прогрессией».

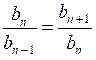 Пусть   = b_{n – 1} · b_{n + 1}, для любого п ≥ 2, так как все числа отличны от нуля, разделим обе части равенства на b_n · b_{n – 1}, получим  . Это означает, что отношение последующего члена к предыдущему – постоянное число, значит, (b_n) – геометрическая прогрессия. 

3. Продолжаем действовать по аналогии. Характеристическое свойство геометрической прогрессии можно переписать и сформулировать по-другому:

 = b_{n – 1} · b_{n + 1},

, то есть модуль любого члена геометрической прогрессии, начиная со второго, является средним геометрическим предыдущего и последующего членов (для арифметической прогрессии речь шла о среднем арифметическом).

IV. Формирование умений и навыков.

В соответствии с поставленными целями на этом уроке следует выполнить следующие группы заданий:

---

Смотрите также файлы

• Отчёт по слесарной практике.docx

• В таблице представлены данные о полезности товара А. Определите среднюю и предельную полезность единицы товара А.docx

• Мишель де монтень Насретдинова П. Д., 329 группа.pptx

• 1. Контакт глазами.docx

• Реферат по дисциплине на тему Экология и здоровье человека.docx