ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1046
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1) Вычисление п-го члена геометрической прогрессии по формуле
(«прямое» применение).
2) Нахождение знаменателя и первого члена прогрессии по формуле п-го члена геометрической прогрессии («не прямое» применение).
3) Использование характеристического свойства геометрической прогрессии для нахождения членов и знаменателя геометрической прогрессии.
4) Комбинированные задания.
Кроме того, в некоторых заданиях не указана явно геометрическая прогрессия – ее необходимо «увидеть», задать, обосновать и только затем решать, используя соответствующие формулы.
Упражнения:
№ 625 (а, б), № 626 (а). «Прямое» применение формулы п-го члена геометрической прогрессии.
№ 630, № 631. «Не прямое» применение формулы п-го члена геометрической прогрессии, либо на использование характеристического свойства геометрической прогрессии.
№ 631 (а).
Р е ш е н и е
(сп) – геометрическая прогрессия;
с5 = –6, с7 = –54.
| I с п о с о б. с5 = с1 · q4 с7 = с1 · q6 |  |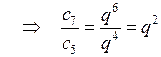
q2 = , q2 = 9, q = 3 или q = –3.
II с п о с о б. | с6 | =
= 18; значит,с6 = 18 или с6 = –18, тогда
q = ; q = = –3 или q = = 3.
О т в е т: 3; –3.
Обычно удобнее решать первым способом, но можно и вторым, способы равносильны.
№ 632 (а), № 633 (б).
№ 629. В этой задаче используются межпредметные связи с геометрией.
А1ВС1 подобен АВС, и коэффициент подобия равен .
Площади этих треугольников относятся как квадраты их соответствующих линейных размеров, значит,
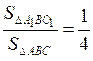, то есть 
.Аналогично докажем, что
. И т. д.
Значения площадей треугольников образуют геометрическую прогрессию (хп), где х1 = 768 и q = . Площадь А9ВС9 равна десятому члену этой прогрессии. Вычислим его:
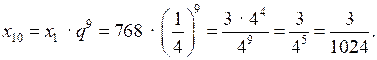
О т в е т:
см2.№ 638. Задача аналогична той, которую решали перед введением понятия геометрической прогрессии.
№ 643. Задание повышенной сложности можно прорешать с учащимися, чтобы закрепить не только навыки применения свойств арифметической и геометрической прогрессии, но и умение действовать по аналогии.
Р е ш е н и е
Пусть a; b; c – арифметическая прогрессия.
По условию a + b + c = 21 (*) и a; (b – 1); (c + 1) – геометрическая прогрессия. По свойству арифметической прогрессии 2b = а + с, значит, из (*) 3b = 21, b = 7.
а + с = 21 – 7 = 14;
с = 14 – а.
По свойству геометрической прогрессии
(b – 1)2 = a · (с + 1);
36 = а (15 – а);
а2 – 15а + 36 = 0;
а = 3 или а = 12, тогда
с = 14 – 3 = 11 или с = 14 – 12 = 2.
О т в е т: 3; 7; 11 или 12; 7; 2.
V. Итоги урока.
Домашнее задание: № 625 (в, г), № 626 (б), № 634, № 639.
У р о к 67 Дата:
НАХОЖДЕНИЕ СУММЫ ПЕРВЫХ пЧЛЕНОВ
ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ
Цели: вывести формулу суммы первых п членов геометрической прогрессии; формировать умение применять эту формулу при решении задач.
Ход урока
I. Организационный момент.
II. Проверочная работа.
В а р и а н т 1
1) Выпишите формулу п члена геометрической прогрессии.
2) В геометрической прогрессии (bп) известны b1 = 1,6 и q = 2. Найдите b5; bk.
3) Найдите первый член геометрической прогрессии (bп), в которой b6 = , q = .
4) Найдите знаменатель геометрической прогрессии, если известно, что b4 = 25, b6 = 16.
В а р и а н т 2
1) Выпишите характеристическое свойство геометрической прогрессии.
2) В геометрической прогрессии (ап) известны а1 = 3,2 и q = . Найдите а4; аk + 1.
3) Найдите первый член геометрической прогрессии (ап), в которой а5 = , q = .
4) Найдите знаменатель геометрической прогрессии (bn), в которой b6 = 100, b8 = 9.
О т в е т ы:
| Задание | Вариант 1 | Вариант 2 |
| 1 | 2 | 3 |
| 1 | bn= b1 · qn – 1 | bn2 = bn – 1 · bn + 1 |
| 1 | 2 | 3 |
| 2 | 25,6; 0,8 · 2k | 0,4; 1,6 · |
| 3 | 9 | |
| 4 | или – | 0,3 или –0,3 |
III. Объяснение нового материала.
1. У с т н а я р а б о т а (актуализация знаний).
Упростить выражение:
а)
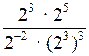; б) ; в) 3п + 1 – 3п – 1.2. Привести легенду об индийском принце и изобретателе шахмат, который в награду за изобретение попросил столько пшеничных зерен, сколько их получится, если на 1-ю клетку положить одно зерно, на вторую – в два раза больше, на третью – в два раза больше, чем на вторую, и т. д. до 64-й клетки.
Количество зерен в клетках составляет геометрическую прогрессию 1; 2; 22; 23; … 263. Если мы сумму обозначим через S, то
S = 1 + 2 + 22 + 23 + … + 263. Домножим обе части на знаменатель геометрической прогрессии:
2S = 2 + 22 + 23 + … + 263 + 264;
2S – S = (2 + 22 + 23 + … + 263 + 264) – (1 + 2 + 22 + 23 + … + 263);
S = 264 – 1.
Если подсчитать это число и перевести на килограммы, то масса превысит триллион тонн.
3. Решая предыдущую задачу, мы уже определим принцип вывода формулы суммы первых п членов геометрической прогрессии.
Повторим эти рассуждения для произвольных b1 и q.
Sп = b1 + b2 + b3 + … bп – 1 + bп; (1)
, так как b1q = b2,
, получаем
. (2)Вычитаем почленно из (2) равенство (1) и получаем
Sn (q – 1) = bnq – b1, тогда
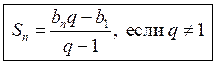  | – формула суммы первых п членов геометрической прогрессии. |
Задать учащимся вопрос: а как быть в случае, когда q =1?
4. Также можно дать задание самостоятельно преобразовать формулу, чтобы выражать сумму только через b1, q и п.
  |
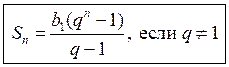IV. Формирование умений и навыков.
Упражнения:
№ 648, № 649 (а, г). Самостоятельное решение упражнений на «прямое» применение формулы II.
№ 651 (а, б), № 653. Решение у доски с комментариями.
№ 654.
Р е ш е н и е
а) (хп) – геометрическая прогрессия; х5 = 1 = ; q = .
х5 = х1 · q4; = х1 ·
; = · х1; х1 = 90.S5 =
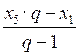; S5 = 
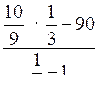= 134 .О т в е т: 134 .
При решении этого примера можно использовать обе формулы нахождения суммы первых п членов геометрической прогрессии, и учащиеся должны уметь выбирать формулу в зависимости от задачной ситуации.
№ 655. Это задание повышенной трудности, для решения которого следует не только подставлять значения в формулу, но и оценивать результат, исключать посторонние решения.
Р е ш е н и е
| а1 > 0, a3 > 0, a5 > 0 а2 < 0, а4 < 0 | q < 0 |
а1 = 2, a5 = 162;
a5 = а1 · q4; 162 = 2 · q4;
q4 = 81;
q = –3, так как q < 0.
S6 = ; S6 =
