Окончание табл.    

1	2
3. Биквадратное ах4 + bх2 + с = 0, а ≠ 0	Метод введения новой переменной. Пусть х2 = t, t ≥ 0, тогда решаем аt2 + bt + c = 0относительно переменной t,а затем из уравнения х2 = t находим значение х
4. Дробно-рациональное. Обе части уравнения являются рациональными выражениями, причем хотя бы одно из них – дробное	А л г о р и т м   р е ш е н и я: 1) найти общий знаменатель дробей, входящих в уравнение; 2) умножить обе части уравнения на общий знаме- натель; 3) решить получившееся целое уравнение; 4) исключить из его корней те, которые обращают в нуль общий знаменатель дробей

IV. Формирование умений и навыков.

Все  упражнения,  решаемые  на  этом  занятии,  можно  разбить  на
г р у п п ы:

– решение уравнений, сводящихся к линейным;

– решение квадратных уравнений;

– решение биквадратных уравнений;

– решение дробно-рациональных уравнений;

– решение уравнений комбинированными методами.

Упражнения:

№ 925 (а, г).

Р е ш е н и е

а) 3х (х  – 1) – 17 = х (1 + 3х) + 1;

    3х² – 3х – 17 = х + 3х² + 1;

                  –4х = 16;

                      х = –4.

г)  ;    · 6

    х – 3 + 6х = 4х – 2 – 12 + 3х;

                 0 = –11 – неверное, значит, нет корней.

О т в е т: а) –4; г) нет корней.

№ 931 (б, г).

Р е ш е н и е

б) 6у² – 0,24 = 0;

    у² =  ;

    у² = 0,04;  у = ± ;  у = ±0,2.

г) 

---

;    · 3;

    10и² + 9и – 9 = 0;

    D = 9² – 4 · 10 · (–9) = 81 + 360 = 441;

    и₁ = 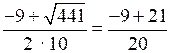  = 0,6;

     и₂ = 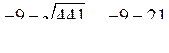  = –1,5.

О т в е т: б) ±0,2; г) 0,6; –1,5.

№ 951 (а).

Р е ш е н и е

4х⁴ – 17х² + 4 = 0.

Пусть х² = t, t ≥ 0, тогда 4t² – 17t + 4 = 0.

D = (–17)² – 4 · 4 · 4 = 289 – 64 = 225;

t₁ = 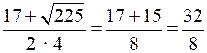  = 4;

t₂ =  ;

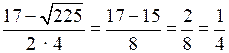х2 = 4           или	х2 =  ;
х1, 2 = ±2;	х3, 4 = ± .

О т в е т: ±2; ± .

№ 940 (б).

Р е ш е н и е

;

;

;

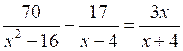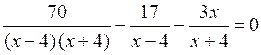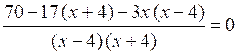х ≠ 4, х ≠ –4; 70 – 17х – 68 – 3х² + 12х = 0;

3х² + 5х – 2 = 0;

D = 5² – 4 · 3 · (–2) = 25 + 24 = 49;

х₁ =  ;

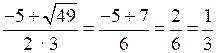х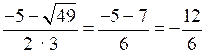₂ =   = –2.

О т в е т:  ; –2.

---

V. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Что называется уравнением? Что означает «решить уравнение»?

– Какие виды уравнений с одной переменной вы знаете?

– Назовите основные методы решения квадратных уравнений.

– Сформулируйте  алгоритм  решения  дробно-рационального  уравнения.

Домашнее задание:  № 925 (б, в),  № 935 (а, в, е),  № 940 (д, ж),  № 951 (в).

У р о к  7 (91).
РЕШЕНИЕ ТЕКСТОВЫХ ЗАДАЧ
НА СОСТАВЛЕНИЕ УРАВНЕНИЙ

Цель: актуализировать умения и навыки решения текстовых задач алгебраическим методом: составлять уравнение по условию задачи и решать его.

Ход урока

I. Организационный момент.

II. Устная работа.

1. Решите уравнение:

а) х² – 4 = 0;             б) 2t – 4t = 0;             в) z² + 5z + 6 = 0.

2. Составьте уравнение для решения задачи:

а) Одно число больше другого на 5, а их произведение равно 126. Найдите эти числа.

б) Гипотенуза прямоугольного треугольника равна 10 см. Найдите катеты треугольника, если один из них на 2 см меньше другого.

в) Какую  часть  числа  составляют  3 %, 10 %, 15 %, 26 %, 50 %, 98 %, а % этого числа?

III. Формирование умений и навыков.

1. А к т у а л и з а ц и я   з н а н и й.

При решении текстовых задач алгебраическим методом основное внимание следует уделять процессу перевода условия задачи на математический язык. Напомним еще раз учащимся основные этапы решения текстовой задачи алгебраическим методом:

1-й  э т а п. Анализ условия задачи и введение переменной.

2-й  э т а п. Перевод условия задачи на математический язык (составление уравнения).

3-й  э т а п. Решение полученного уравнения.

4-й  э т а п. Интерпретация полученного результата.

Самым важным и сложным для учащихся являются первые два этапа. Чтобы преодолеть эти трудности, необходима наглядность в представлении условия. С этой целью напоминаем, что данные условия можно заносить в таблицы, составлять схемы, графы.

Также следует уделить внимание 4-му этапу. Учащиеся должны понимать, какие результаты удовлетворяют условию задачи, а какие нет (определение правдоподобности).

---

2. Т е к с т о в ы е   з а д а ч и  можно условно разбить на группы по типу уравнения:

а) сводящиеся к линейному уравнению;

б) сводящиеся к квадратному уравнению;

в) сводящиеся к дробно-рациональному уравнению.

Также задачи можно классифицировать по фабуле:

а) задачи «на движение»;

б) задачи «на работу»;

в) задачи «на проценты и концентрацию».

Упражнения:

№ 928.

Р е ш е н и е

А н а л и з:

	V (км/ч)	t (ч)	S (км)
Пешеход	х	1,5 + 0,5	26
Велосипедист	х + 8	1,5

Пусть  х км/ч – скорость  пешехода,  тогда (х + 8) км/ч – скорость велосипедиста. Велосипедист ехал 1,5 ч, а пешеход шел 2 ч, так как вышел на 0,5 ч раньше велосипедиста. Зная, что суммарно до встречи они преодолели 26 км, составим уравнение:

2 · х + 1,5 (х + 8) = 26;

2х + 1,5х + 12 = 26;

3,5х = 14;

 х = 4.

4 (км/ч) – скорость  пешехода, следовательно, скорость  велосипедиста  равна 4 + 8 = 12 (км/ч).

О т в е т: 4 км/ч; 12 км/ч.

№ 930.

Р е ш е н и е

А н а л и з:

Раствор	Соль (г)	Вода (г)	Всего (г)
20 %	60	240	300
8 %	60	240 + х	300 + х

В 300 г 20 %-го раствора соли содержится 0,2 · 300 = 60 г соли.

Пусть  в  раствор  добавили х г  воды,  тогда  общая  масса  раствора стала (300 + х) г. Абсолютное содержание соли в растворе не изменилось и составляет 60 г. Зная, что относительное содержание соли в растворе составило теперь 8 %, получим уравнение:

0,08 · (300 + х) = 60;

24 + 0,08х = 60;

 0,08х = 36;

 х = 450.

О т в е т: 450 г.

№ 936.

Р е ш е н и е

А н а л и з:

(х + 15) м
	х м

---

Пусть х м – ширина участка, тогда (х + 15) м – его длина. Зная, что площадь участка составляет 700 м², получаем уравнение:

х (х + 15) = 700;

х² + 15х – 700 = 0;

D = (15)² – 4 · 1 · (–700) = 225 + 2800 = 3025;

x₁ = 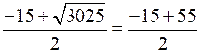   = 20;

x₁ = 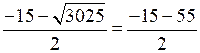  = –35 – не имеет смысла.

И м е е м: 20 м – ширина участка, 35 м – его длина.

Длина изгороди равна 2 · (35 + 20) м, что составляет 110 м.

О т в е т: 110 м.

№ 937.

Р е ш е н и е

Пусть в классе п учеников. Так как каждый раздал свое фото оставшимся (п – 1) ученикам, то всего было роздано фотографий п(п – 1). Зная, что всего передано 600 фотокарточек, составим уравнение:

п(п – 1) = 600;

п² – п – 600 = 0;

D = (–1)² – 4 · 1 · (–600) = 2401;

n₁ = 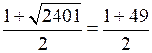  = 25;

n₁ = 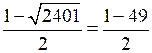  = –24 – не имеет смысла.

О т в е т: 25 учеников.

№ 941.

Р е ш е н и е

А н а л и з:

Бригады	p	t		A
I, II	p1 + p2	6		1
I	p1		> на 5	1
II	p2			1

Пусть х – производительность первой бригады, тогда 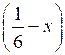  – производительность  второй  бригады.  Первая  бригада  выполнит  всю  работу за   ч, а вторая бригада – за   ч, что составляет   ч. Зная, что первая бригада затратит на 5 ч больше, составим уравнение:

 + 5;

---

Смотрите также файлы

• Отчёт по слесарной практике.docx

• В таблице представлены данные о полезности товара А. Определите среднюю и предельную полезность единицы товара А.docx

• Мишель де монтень Насретдинова П. Д., 329 группа.pptx

• 1. Контакт глазами.docx

• Реферат по дисциплине на тему Экология и здоровье человека.docx