ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1028
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
= 0;
х ≠ 0, х ≠ ; 1 – 12х – 5х + 30х2 = 0;
30х2 – 17х + 1 = 0;
D = (–17)2 – 4 · 30 · 1 = 289 – 120 = 169;
x1 =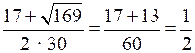
;
x2 =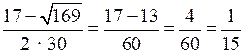
.
x = – не удовлетворяет условию задачи, иначе обе бригады выполнили бы работу за одинаковое время. Так как t = , то первая бригада выполнит работу за 15 ч, а вторая за 10 ч.
О т в е т: 15 ч, 10 ч.
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– В чем суть алгебраического метода решения текстовой задачи?
– Охарактеризуйте основные этапы решения текстовой задачи.
– Как интерпретируются полученные результаты? Приведите примеры неправдоподобных результатов для задач «на движение», «на работу», «на смеси и концентрацию».
Домашнее задание: № 929, № 939, № 944, № 950.
У р о к 8 (92).
РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ
Цели: систематизировать знания учащихся по теме; актуализировать умения и навыки решения систем уравнений с двумя неизвестными первой и второй степени.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Выразите одну переменную через другую из уравнения:
а) 5х + 2у = –6; б) ху – 3 = 0.
2. Определите, из какого уравнения системы какую переменную удобнее выразить:
а)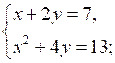
б) 
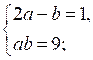в)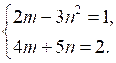 
3. Решите систему уравнений:
а)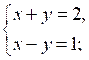
б)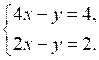 
III. Формирование умений и навыков.
Перед решением упражнений следует повторить основные способы решения систем уравнений с двумя неизвестными:
1) способ подстановки
;
2) способ сложения;
3) графический.
Упражнения:
№ 957 (а).
Р е ш е н и е
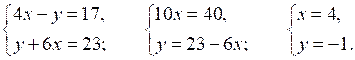
О т в е т: (4; –1).
№ 958 (б).
Р е ш е н и е
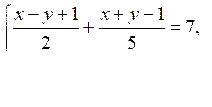
Обозначим х – у + 1 = а, х + у – 1 = b.
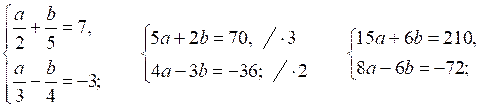
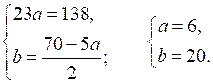
И м е е м: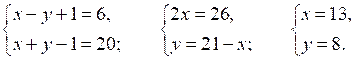
О т в е т: (13; 8).
№ 961.
Р е ш е н и е
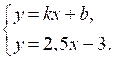
а) Чтобы система не имела решений, приравняем значения у:
kx + b = 2,5x – 3;
(k – 2,5) х = –3 – b.
Если k – 2,5 = 0, а –3 – b ≠ 0, то нет решений.
Пусть k = 2,5, b = 1.
б) Чтобы система имела бесконечно много решений, необходимо, чтобы k = 2,5, b = –3.
в) Если х = 4 – входит в решение, то у = 2,5 · 4 – 3;
у = 7, тогда 7 = k · 4 + b, например, k = 1, b = 3.
О т в е т: а) k = 2,5, b = 1; б) k = 2,5, b = –3; в) k = 1, b = 3.
№ 963 (а).
Р е ш е н и е
Прямая задается уравнением у = kx + b. Так как точки (0; 30) и (6; 0) принадлежат этой прямой, то
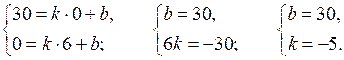
Уравнение прямой: у = –5х + 30.
О т в е т: у = –5х + 30.
№ 972 (а).
Р е ш е н и е
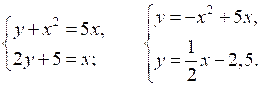
Построим графики функций у = –х2 + 5х и у = х – 2,5 и найдем координаты их точек пересечения.
1) у = –х2 + 5х. Графиком является парабола, проходящая через точки (0; 0), (5; 0), вершина параболы (2,5; 6,25), ветви направлены вниз.
2) у = х – 2,5. Графиком является прямая, проходящая через точки (0; –2,5),(5; 0).
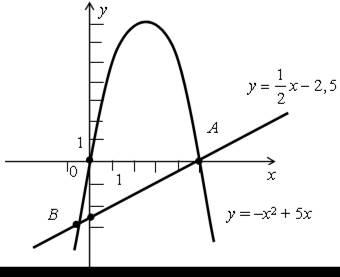
А (5; 0), В (–0,5; –2,75).
О т в е т: (5; 0), (–0,5; –2,75).
№ 973 (б).
Р е ш е н и е
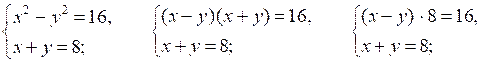
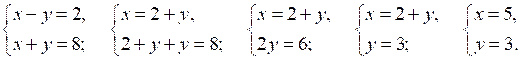
О т в е т: (5; 3).
№ 974 (а).
Р е ш е н и е
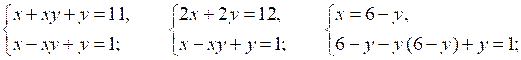
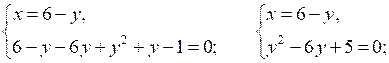
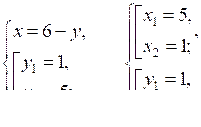
О т в е т: (5; 1), (1; 5).
№ 975 (а, б).
Р е ш е н и е
а)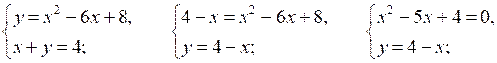
б)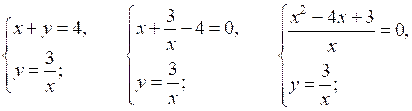
О т в е т: а) (4; 0); (1; 3); б) (1; 3); (3; 1).
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Как найти координаты точек пересечения графиков уравнений?
– В чем состоит способ сложения при решении систем уравнений?
– Каков алгоритм решения систем уравнений способом подстановки?
– Любую ли систему линейных уравнений можно решить способом сложения? Способом подстановки?
– Можно ли решить способом сложения систему, содержащую нелинейные уравнения? Когда это возможно?
Домашнее задание: № 958 (а), № 962 (а), № 972 (б), № 973 (д),
№ 976*.
У р о к 9 (93).
РЕШЕНИЕ ТЕКСТОВЫХ ЗАДАЧ
НА СОСТАВЛЕНИЕ СИСТЕМ УРАВНЕНИЙ
Цели: актуализировать умения и навыки решения текстовых задач алгебраическим методом: составлять систему уравнений по условию задачи и решать ее.
Ход урока
I. Организационный момент.
II. Проверочная работа.
В а р и а н т 1
Решите систему уравнений:
1.
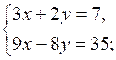2. 
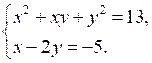
В а р и а н т 2
Решите систему уравнений:
1.
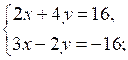2. 
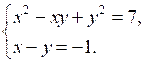
Р е ш е н и е
В а р и а н т 1
1.
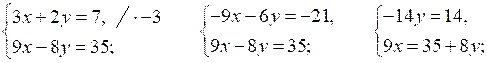
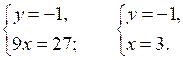
О т в е т: (3; –1).
2.
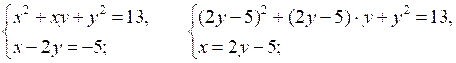
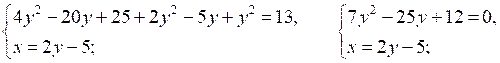
D = (–25)2 – 4 · 7 · 12 = 625 – 336 = 289 = (17)2;
y1 =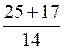
= 3; y2 = 
.
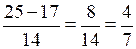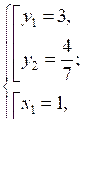
О т в е т: (1; 3);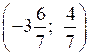
.
В а р и а н т 2
1.
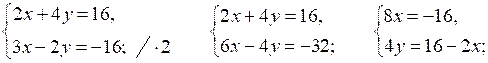
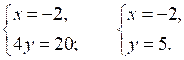
О т в е т: (–2; 5).
2.
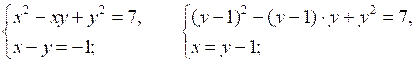
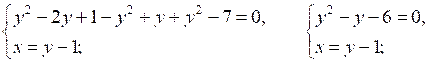
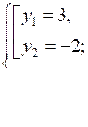
О т в е т: (2; 3); (–3; –2).
III. Формирование умений и навыков.
Все задания условно можно разбить на г р у п п ы:
– Текстовые задачи на составление системы линейных уравнений с двумя неизвестными.
– Текстовые задачи на составление системы уравнений второй степени.
– Текстовые задачи на составление систем уравнений с использованием формул из различных разделов математики.
Как и в случае с задачами на составление уравнений, следует особое внимание уделять анализу условия задачи и его переводу на математический язык.
Упражнения:
№ 966.
Р е ш е н и е
А н а л и з:
Пусть х и у – количество деталей, которые мастер и ученик изготовили в первый день соответственно. Во второй день мастер изготовил на 20 % больше, чем в первый день, что составило 1,2х деталей, а ученик во второй день изготовил на 10 % больше, что составило 1,1у. Зная, что всего в первый день было изготовлено 100 деталей, а во второй – 116 деталей, составим систему уравнений:
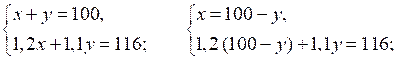
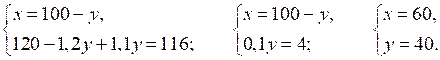
О т в е т: 60; 40.
№ 970.
Р е ш е н и е
А н а л и з:
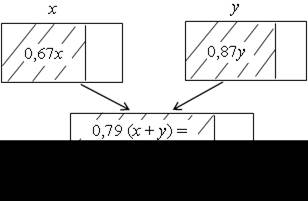
Пусть х и у – количество первого и второго сплава соответственно.
Первый сплав содержит 0,67х меди, второй – 0,87у. Масса нового сплава (х + у), и меди в нем 79 %, то есть 0,79 (
х ≠ 0, х ≠ ; 1 – 12х – 5х + 30х2 = 0;
30х2 – 17х + 1 = 0;
D = (–17)2 – 4 · 30 · 1 = 289 – 120 = 169;
x1 =
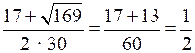;x2 =
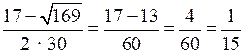.x = – не удовлетворяет условию задачи, иначе обе бригады выполнили бы работу за одинаковое время. Так как t = , то первая бригада выполнит работу за 15 ч, а вторая за 10 ч.
О т в е т: 15 ч, 10 ч.
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– В чем суть алгебраического метода решения текстовой задачи?
– Охарактеризуйте основные этапы решения текстовой задачи.
– Как интерпретируются полученные результаты? Приведите примеры неправдоподобных результатов для задач «на движение», «на работу», «на смеси и концентрацию».
Домашнее задание: № 929, № 939, № 944, № 950.
У р о к 8 (92).
РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ
Цели: систематизировать знания учащихся по теме; актуализировать умения и навыки решения систем уравнений с двумя неизвестными первой и второй степени.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Выразите одну переменную через другую из уравнения:
а) 5х + 2у = –6; б) ху – 3 = 0.
2. Определите, из какого уравнения системы какую переменную удобнее выразить:
а)
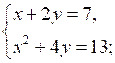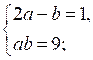б) в) 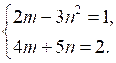3. Решите систему уравнений:
а)
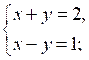б) 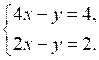III. Формирование умений и навыков.
Перед решением упражнений следует повторить основные способы решения систем уравнений с двумя неизвестными:
1) способ подстановки
;
2) способ сложения;
3) графический.
Упражнения:
№ 957 (а).
Р е ш е н и е
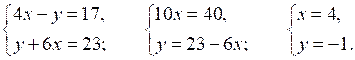
О т в е т: (4; –1).
№ 958 (б).
Р е ш е н и е
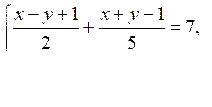
Обозначим х – у + 1 = а, х + у – 1 = b.
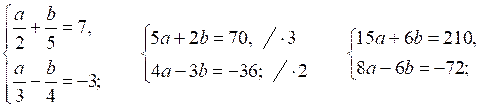
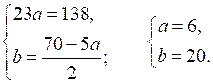
И м е е м:
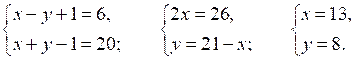
О т в е т: (13; 8).
№ 961.
Р е ш е н и е
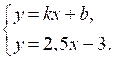
а) Чтобы система не имела решений, приравняем значения у:
kx + b = 2,5x – 3;
(k – 2,5) х = –3 – b.
Если k – 2,5 = 0, а –3 – b ≠ 0, то нет решений.
Пусть k = 2,5, b = 1.
б) Чтобы система имела бесконечно много решений, необходимо, чтобы k = 2,5, b = –3.
в) Если х = 4 – входит в решение, то у = 2,5 · 4 – 3;
у = 7, тогда 7 = k · 4 + b, например, k = 1, b = 3.
О т в е т: а) k = 2,5, b = 1; б) k = 2,5, b = –3; в) k = 1, b = 3.
№ 963 (а).
Р е ш е н и е
Прямая задается уравнением у = kx + b. Так как точки (0; 30) и (6; 0) принадлежат этой прямой, то
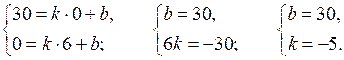
Уравнение прямой: у = –5х + 30.
О т в е т: у = –5х + 30.
№ 972 (а).
Р е ш е н и е
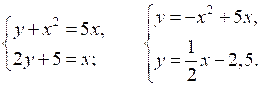
Построим графики функций у = –х2 + 5х и у = х – 2,5 и найдем координаты их точек пересечения.
1) у = –х2 + 5х. Графиком является парабола, проходящая через точки (0; 0), (5; 0), вершина параболы (2,5; 6,25), ветви направлены вниз.
2) у = х – 2,5. Графиком является прямая, проходящая через точки (0; –2,5),(5; 0).
А (5; 0), В (–0,5; –2,75).
О т в е т: (5; 0), (–0,5; –2,75).
№ 973 (б).
Р е ш е н и е
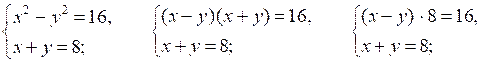
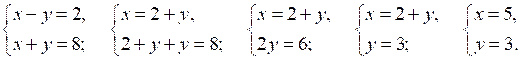
О т в е т: (5; 3).
№ 974 (а).
Р е ш е н и е
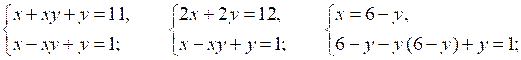
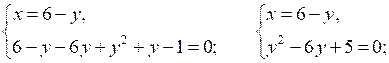
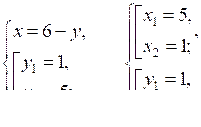
О т в е т: (5; 1), (1; 5).
№ 975 (а, б).
Р е ш е н и е
а)
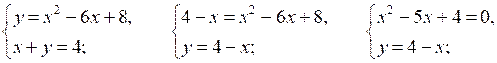
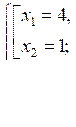 А (1; 3); В (4; 0) |  |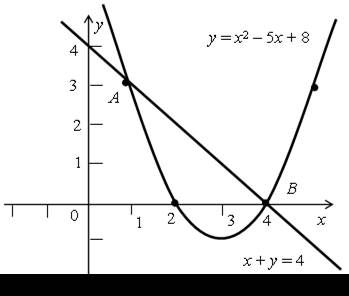
б)
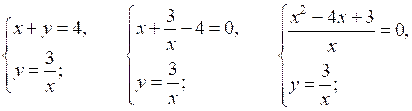
| А (1; 3); В (3; 1) |  |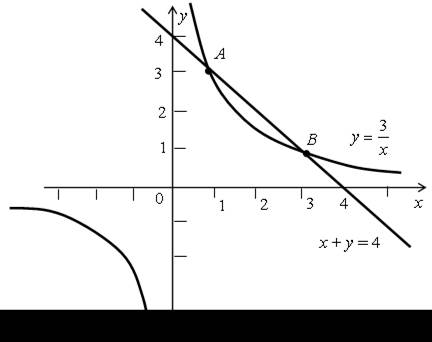
О т в е т: а) (4; 0); (1; 3); б) (1; 3); (3; 1).
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Как найти координаты точек пересечения графиков уравнений?
– В чем состоит способ сложения при решении систем уравнений?
– Каков алгоритм решения систем уравнений способом подстановки?
– Любую ли систему линейных уравнений можно решить способом сложения? Способом подстановки?
– Можно ли решить способом сложения систему, содержащую нелинейные уравнения? Когда это возможно?
Домашнее задание: № 958 (а), № 962 (а), № 972 (б), № 973 (д),
№ 976*.
У р о к 9 (93).
РЕШЕНИЕ ТЕКСТОВЫХ ЗАДАЧ
НА СОСТАВЛЕНИЕ СИСТЕМ УРАВНЕНИЙ
Цели: актуализировать умения и навыки решения текстовых задач алгебраическим методом: составлять систему уравнений по условию задачи и решать ее.
Ход урока
I. Организационный момент.
II. Проверочная работа.
В а р и а н т 1
Решите систему уравнений:
1.
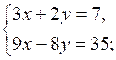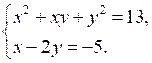
2. В а р и а н т 2
Решите систему уравнений:
1.
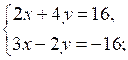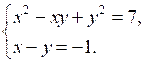
2. Р е ш е н и е
В а р и а н т 1
1.
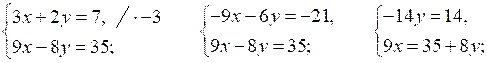
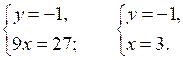
О т в е т: (3; –1).
2.
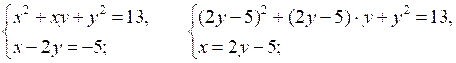
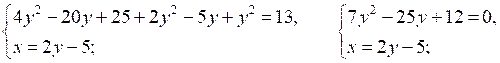
D = (–25)2 – 4 · 7 · 12 = 625 – 336 = 289 = (17)2;
y1 =
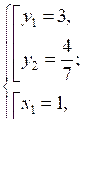
= 3; y2 = . О т в е т: (1; 3);
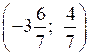.В а р и а н т 2
1.
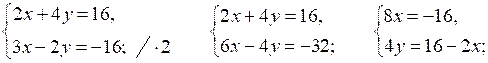
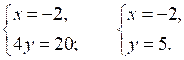
О т в е т: (–2; 5).
2.
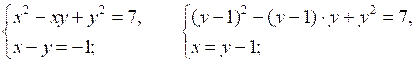
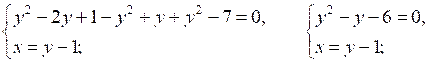
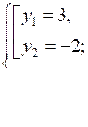
О т в е т: (2; 3); (–3; –2).
III. Формирование умений и навыков.
Все задания условно можно разбить на г р у п п ы:
– Текстовые задачи на составление системы линейных уравнений с двумя неизвестными.
– Текстовые задачи на составление системы уравнений второй степени.
– Текстовые задачи на составление систем уравнений с использованием формул из различных разделов математики.
Как и в случае с задачами на составление уравнений, следует особое внимание уделять анализу условия задачи и его переводу на математический язык.
Упражнения:
№ 966.
Р е ш е н и е
А н а л и з:
| | Мастер | Ученик | Всего |
| I день | х | у | 100 |
| II день | 1,2х | 1,1у | 116 |
Пусть х и у – количество деталей, которые мастер и ученик изготовили в первый день соответственно. Во второй день мастер изготовил на 20 % больше, чем в первый день, что составило 1,2х деталей, а ученик во второй день изготовил на 10 % больше, что составило 1,1у. Зная, что всего в первый день было изготовлено 100 деталей, а во второй – 116 деталей, составим систему уравнений:
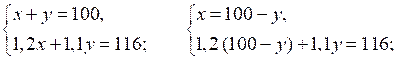
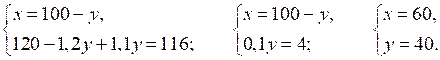
О т в е т: 60; 40.
№ 970.
Р е ш е н и е
А н а л и з:
Пусть х и у – количество первого и второго сплава соответственно.
Первый сплав содержит 0,67х меди, второй – 0,87у. Масса нового сплава (х + у), и меди в нем 79 %, то есть 0,79 (