ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1027
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
х + у). Зная, что абсолютная масса меди в новом сплаве составляет 0,67х + 0,87у, составим уравнение с двумя неизвестными:
0,79 (х + у) = 0,67х + 0,87у;
0,79х – 0,67х = 0,87у – 0,79у;
0,12х = 0,08у;
;
.
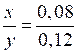О т в е т: 2 : 3.
П р и м е ч а н и е. При решении этой задачи система уравнений не составляется, так как требуется установить только соотношение сплавов. Можно предложить учащимся самостоятельно дополнить условие задачи, чтобы она сводилась к решению системы уравнений, имеющей единственное решение.
№ 982.
Р е ш е н и е
Пусть х и у (см) – катеты прямоугольного треугольника, тогда его площадь равна · х · у (см2) и составляет 44 (см2). Если один из катетов уменьшить на 1 см, а другой увеличить на 2 см, то его площадь будет равна (х – 1)(у + 2). Зная, что эта площадь равна 50 см2, составим систему уравнений:
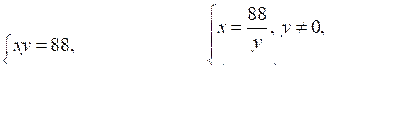
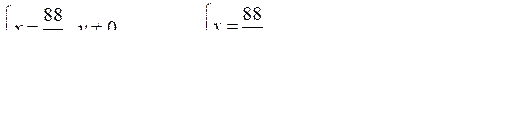
О т в е т: 11; 8.
№ 989.
Р е ш е н и е
А н а л и з: (ап) – арифметическая прогрессия.
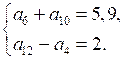
а25 – ?
Пусть а – первый член арифметической прогрессии, d – ее разность, тогда а6 = а + 5d, а10 = а + 9d и а6 + а10 = 2а + 14d; а12 = а + 11d; а4 = а +
+ 3d и а12 – а4 = 8d. Зная, что а6 + а10 = 5,9 и а12 – а4 = 2, составим систему уравнений:
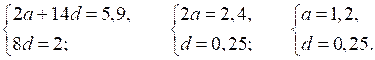
а25 = а + 24d; а25 = 1,2 + 24 · 0,25 = 7,2.
О т в е т: 7,2.
№ 996.
А н а л и з: (bn
) – геометрическая прогрессия.
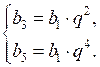
S7 – ?
Пусть b1 > 0 – первый член геометрической прогрессии, q > 0 – ее знаменатель, тогда b3 = b1 · q2 и b5 = b1 · q4. Зная, что b3 = 20 и b5 = 80, составим систему уравнений:
П р и м е ч а н и е. Решение q = –2 – не удовлетворяет условию задачи.
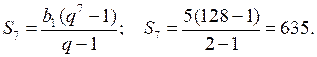
О т в е т: 635.
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Каковы этапы решения задач на составление систем уравнений?
– В чем состоит способ сложения и способ подстановки при решении систем уравнений?
Домашнее задание: № 967, № 980, № 984, № 997.
У р о к 10 (94).
ЛИНЕЙНЫЕ НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ
И СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ
С ОДНОЙ ПЕРЕМЕННОЙ
Цели: систематизировать знания учащихся по теме; актуализировать умения и навыки решения неравенств и систем неравенств с одной переменной.
Ход урока
I. Организационный момент.
II. Повторение учебного материала.
1. Свойства числовых неравенств.
2. Неравенство первой степени kx + b > 0, где х – переменная, k, b – числа, k ≠ 0.
3. Решение неравенства с одной переменной, число х0 – такое, что k · x0 + b > 0 – верное.
4. Решить неравенство – найти все его решения или доказать, что их нет.
5. Два неравенства называются равносильными, если любое решение первого неравенства является решением второго и наоборот.
6. Свойства неравенств с одной переменной:
– Члены неравенства можно переносить с противоположными знаками из одной части неравенства в другую.
– В неравенстве можно приводить подобные члены.
– При умножении (или делении) неравенства на положительное число знак неравенства сохраняется.
– При умножении (или делении) неравенства на отрицательное число знак неравенства меняется на противоположный.
III. Математический диктант.
В а р и а н т 1 [В а р и а н т 2]
1. Запишите числовой промежуток, служащий множеством решений неравенства х ≤ 3 [у > –8].
2. Запишите неравенство, множеством решений которого служит промежуток (–3; +∞) [(–∞; 7)].
3. Изобразите на координатной прямой промежуток (–2; 3] [[–1; 4)] и запишите неравенство, множеством решений которого он служит.
4. Решите неравенство: 2х – 1 ≤ 2 (х – 1) [3(х – 1) ≥ 3х + 1].
5. Решите неравенство: 5у – 10 > 10у – 5 [3x – 6 < 6x – 3].
6. Решите неравенство: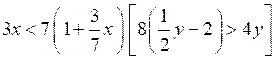
.
О т в е т ы:
В а р и а н т 1 [В а р и а н т 2]
1. (–∞; 3] [(–8; +∞)].
2. х > –3 [x < 7].
3. –2 < х ≤ 3 [–1 ≤ х < 4].
4. Нет решений [х – любое].
5. (–∞; –1) [(–1; +∞)].
6. х – любое [нет решений].
IV. Формирование умений и навыков.
Особое внимание обращаем на верное использование свойств неравенства, а также на возможность графической интерпретации полученных решений.
Упражнения:
№ 1000.
Р е ш е н и е
в) 2,6 < < 2,7;
2,2 < < 2,3;
5,72 < < 6,21.
№ 1001 (а, в, з).
Р е ш е н и е
а) 0,3 (2т – 3) < 3 (0,6т + 1,3);
0,6т – 0,9 < 1,8т + 3,9;
–1,2т < 4,8;
т > –4.
(–4; +∞).
в) 10 – 5 (0,3а – 0,2) ≥ 5 – 10 (0,1а + 0,2);
10 – 1,5а + 1 ≥ 5 – а – 2;
–0,5а ≥ –8;
а ≤ 16.
(–∞; 16].
з) (1 –3,6а) (0,2а+ 3) + (4+ 0,9а) (0,8а + 10) ≤ 42,2;
0,2а + 3 – 0,72а2 – 10,8а + 3,2а + 40 + 0,72а2 + 9а ≤ 42,2;
1,6а ≤ –0,8;
а ≤ –0,5.
(–∞; –0,5].
О т в е т: а) (–4; +∞); в) (–∞; 16]; з) (–∞; –0,5].
№ 1002 (в, е).
Р е ш е н и е
в)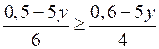
;
2 (0,5 – 5у) ≥ 3 (0,6 – 5у);
1 – 10у ≥ 1,8 – 15у;
5у ≥ 0,8;
у ≥ 0,16.
е)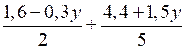
< –4,05у;
5 (1,6 – 0,3у) + 2 (4,4 + 1,5у) + 10 · 4,05 · у < 0;
8 – 1,5у + 8,8 + 3у + 40,5у < 0;
42у < –16,8;
у < –0,4.
О т в е т: в) у ≥ 0,16; е) у < –0,4.
№ 1004 (а, в).
Р е ш е н и е
а) (5 – 2х) ( – 3) < 0;
2,4 < < 2,5;
–0,6 < – 3 < –0,5, значит, – 3 < 0.
Разделим обе части неравенства на ( – 3), получим:
5 – 2х > 0; –2х > –5; х < 2,5.
в)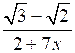
< 0; 1,4 < < 1,5;
–1,5< – < 1,4;
1,7 < < 1,8;
0,2 < – < 0,4, значит, – > 0.
Разделим обе части неравенства на ( – ): < 0. Дробь меньше нуля, если знаменатель меньше нуля:
2 + 7х < 0;
7х < –2;
х < – .
О т в е т: а) (–∞; 2,5); в) (–∞; – ).
№ 1005 (в, г).
Р е ш е н и е
в)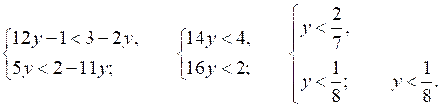
г)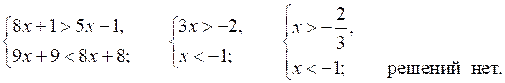
О т в е т: в) (–∞; ); г) нет решений.
№ 1008 (б).
Р е ш е н и е
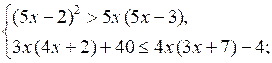
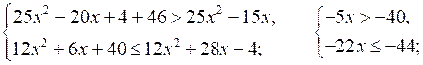
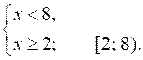
В этот интервал входят целые числа 2; 3; 4; 5; 6; 7.
О т в е т: 2; 3; 4; 5; 6; 7.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что называется линейным неравенством с одним неизвестным?
– Какие есть утверждения о равносильности неравенств?
– Каким способом можно решить систему линейных неравенств?
Домашнее задание: № 1001 (б, г, е), № 1003, № 1004 (б), № 1007 (б).
У р о к 11 (95).
НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ
С ОДНОЙ ПЕРЕМЕННОЙ ВТОРОЙ СТЕПЕНИ
Цели: систематизировать знания учащихся по теме; актуализировать умения и навыки решения неравенств и систем неравенств с одной переменной второй степени.
Ход урока
I. Организационный момент.
II. Математический диктант.
В а р и а н т 1 [В а р и а н т 2]
1. Является ли число –3 решением системы неравенств?
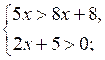
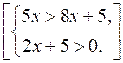
2. Запишите решение системы неравенств:
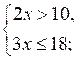
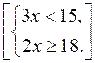
3. Запишите решение системы неравенств:
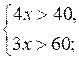
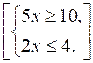
4. Запишите решение системы неравенств:
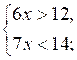
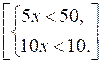
5. Решите систему неравенств:
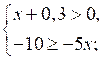
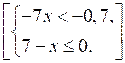
О т в е т ы:
В а р и а н т 1 [В а р и а н т 2]
1. Нет [нет].
2. (5; 6] [(5;9]].
3. (20;+∞) [{2}].
4. Нет решений [(–∞;1)].
5. [2;+∞) [[7;+∞)].
0,79 (х + у) = 0,67х + 0,87у;
0,79х – 0,67х = 0,87у – 0,79у;
0,12х = 0,08у;
;.
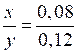О т в е т: 2 : 3.
П р и м е ч а н и е. При решении этой задачи система уравнений не составляется, так как требуется установить только соотношение сплавов. Можно предложить учащимся самостоятельно дополнить условие задачи, чтобы она сводилась к решению системы уравнений, имеющей единственное решение.
№ 982.
Р е ш е н и е
Пусть х и у (см) – катеты прямоугольного треугольника, тогда его площадь равна · х · у (см2) и составляет 44 (см2). Если один из катетов уменьшить на 1 см, а другой увеличить на 2 см, то его площадь будет равна (х – 1)(у + 2). Зная, что эта площадь равна 50 см2, составим систему уравнений:
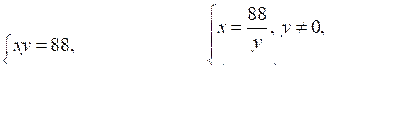
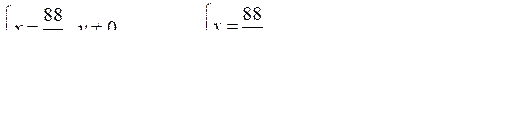
О т в е т: 11; 8.
№ 989.
Р е ш е н и е
А н а л и з: (ап) – арифметическая прогрессия.
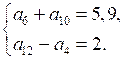
а25 – ?
Пусть а – первый член арифметической прогрессии, d – ее разность, тогда а6 = а + 5d, а10 = а + 9d и а6 + а10 = 2а + 14d; а12 = а + 11d; а4 = а +
+ 3d и а12 – а4 = 8d. Зная, что а6 + а10 = 5,9 и а12 – а4 = 2, составим систему уравнений:
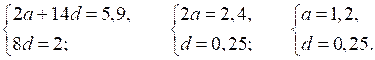
а25 = а + 24d; а25 = 1,2 + 24 · 0,25 = 7,2.
О т в е т: 7,2.
№ 996.
А н а л и з: (bn
) – геометрическая прогрессия.
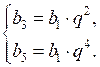
S7 – ?
Пусть b1 > 0 – первый член геометрической прогрессии, q > 0 – ее знаменатель, тогда b3 = b1 · q2 и b5 = b1 · q4. Зная, что b3 = 20 и b5 = 80, составим систему уравнений:
П р и м е ч а н и е. Решение q = –2 – не удовлетворяет условию задачи.
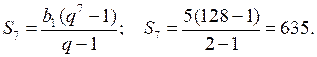
О т в е т: 635.
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Каковы этапы решения задач на составление систем уравнений?
– В чем состоит способ сложения и способ подстановки при решении систем уравнений?
Домашнее задание: № 967, № 980, № 984, № 997.
У р о к 10 (94).
ЛИНЕЙНЫЕ НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ
И СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ
С ОДНОЙ ПЕРЕМЕННОЙ
Цели: систематизировать знания учащихся по теме; актуализировать умения и навыки решения неравенств и систем неравенств с одной переменной.
Ход урока
I. Организационный момент.
II. Повторение учебного материала.
1. Свойства числовых неравенств.
2. Неравенство первой степени kx + b > 0, где х – переменная, k, b – числа, k ≠ 0.
3. Решение неравенства с одной переменной, число х0 – такое, что k · x0 + b > 0 – верное.
4. Решить неравенство – найти все его решения или доказать, что их нет.
5. Два неравенства называются равносильными, если любое решение первого неравенства является решением второго и наоборот.
6. Свойства неравенств с одной переменной:
– Члены неравенства можно переносить с противоположными знаками из одной части неравенства в другую.
– В неравенстве можно приводить подобные члены.
– При умножении (или делении) неравенства на положительное число знак неравенства сохраняется.
– При умножении (или делении) неравенства на отрицательное число знак неравенства меняется на противоположный.
III. Математический диктант.
В а р и а н т 1 [В а р и а н т 2]
1. Запишите числовой промежуток, служащий множеством решений неравенства х ≤ 3 [у > –8].
2. Запишите неравенство, множеством решений которого служит промежуток (–3; +∞) [(–∞; 7)].
3. Изобразите на координатной прямой промежуток (–2; 3] [[–1; 4)] и запишите неравенство, множеством решений которого он служит.
4. Решите неравенство: 2х – 1 ≤ 2 (х – 1) [3(х – 1) ≥ 3х + 1].
5. Решите неравенство: 5у – 10 > 10у – 5 [3x – 6 < 6x – 3].
6. Решите неравенство:
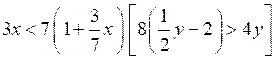.О т в е т ы:
В а р и а н т 1 [В а р и а н т 2]
1. (–∞; 3] [(–8; +∞)].
2. х > –3 [x < 7].
3. –2 < х ≤ 3 [–1 ≤ х < 4].
4. Нет решений [х – любое].
5. (–∞; –1) [(–1; +∞)].
6. х – любое [нет решений].
IV. Формирование умений и навыков.
Особое внимание обращаем на верное использование свойств неравенства, а также на возможность графической интерпретации полученных решений.
Упражнения:
№ 1000.
Р е ш е н и е
| а) 2,6 < < 2,7; 2,2 < < 2,3; 4,8 < + < 5. | б) 2,2 < < 2,3; –2,3 < – < –2,2; 2,6 < < 2,7; 0,3 < – < 0,5. |
в) 2,6 < < 2,7;
2,2 < < 2,3;
5,72 < < 6,21.
№ 1001 (а, в, з).
Р е ш е н и е
а) 0,3 (2т – 3) < 3 (0,6т + 1,3);
0,6т – 0,9 < 1,8т + 3,9;
–1,2т < 4,8;
т > –4.
(–4; +∞).
в) 10 – 5 (0,3а – 0,2) ≥ 5 – 10 (0,1а + 0,2);
10 – 1,5а + 1 ≥ 5 – а – 2;
–0,5а ≥ –8;
а ≤ 16.
(–∞; 16].
з) (1 –3,6а) (0,2а+ 3) + (4+ 0,9а) (0,8а + 10) ≤ 42,2;
0,2а + 3 – 0,72а2 – 10,8а + 3,2а + 40 + 0,72а2 + 9а ≤ 42,2;
1,6а ≤ –0,8;
а ≤ –0,5.
(–∞; –0,5].
О т в е т: а) (–4; +∞); в) (–∞; 16]; з) (–∞; –0,5].
№ 1002 (в, е).
Р е ш е н и е
в)
;2 (0,5 – 5у) ≥ 3 (0,6 – 5у);
1 – 10у ≥ 1,8 – 15у;
5у ≥ 0,8;
у ≥ 0,16.
е)
< –4,05у;
5 (1,6 – 0,3у) + 2 (4,4 + 1,5у) + 10 · 4,05 · у < 0;
8 – 1,5у + 8,8 + 3у + 40,5у < 0;
42у < –16,8;
у < –0,4.
О т в е т: в) у ≥ 0,16; е) у < –0,4.
№ 1004 (а, в).
Р е ш е н и е
а) (5 – 2х) ( – 3) < 0;
2,4 < < 2,5;
–0,6 < – 3 < –0,5, значит, – 3 < 0.
Разделим обе части неравенства на ( – 3), получим:
5 – 2х > 0; –2х > –5; х < 2,5.
в)
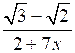< 0; 1,4 < < 1,5;–1,5< – < 1,4;
1,7 < < 1,8;
0,2 < – < 0,4, значит, – > 0.
Разделим обе части неравенства на ( – ): < 0. Дробь меньше нуля, если знаменатель меньше нуля:
2 + 7х < 0;
7х < –2;
х < – .
О т в е т: а) (–∞; 2,5); в) (–∞; – ).
№ 1005 (в, г).
Р е ш е н и е
в)
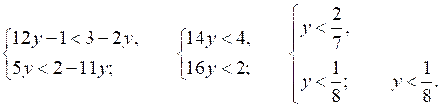
г)
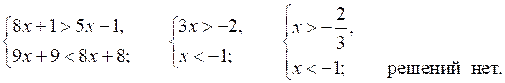
О т в е т: в) (–∞; ); г) нет решений.
№ 1008 (б).
Р е ш е н и е
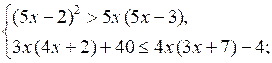
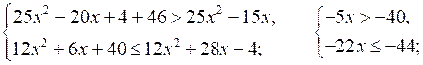
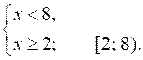
В этот интервал входят целые числа 2; 3; 4; 5; 6; 7.
О т в е т: 2; 3; 4; 5; 6; 7.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что называется линейным неравенством с одним неизвестным?
– Какие есть утверждения о равносильности неравенств?
– Каким способом можно решить систему линейных неравенств?
Домашнее задание: № 1001 (б, г, е), № 1003, № 1004 (б), № 1007 (б).
У р о к 11 (95).
НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ
С ОДНОЙ ПЕРЕМЕННОЙ ВТОРОЙ СТЕПЕНИ
Цели: систематизировать знания учащихся по теме; актуализировать умения и навыки решения неравенств и систем неравенств с одной переменной второй степени.
Ход урока
I. Организационный момент.
II. Математический диктант.
В а р и а н т 1 [В а р и а н т 2]
1. Является ли число –3 решением системы неравенств?
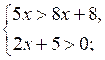
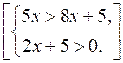
2. Запишите решение системы неравенств:
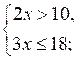
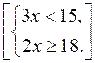
3. Запишите решение системы неравенств:
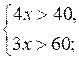
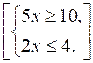
4. Запишите решение системы неравенств:
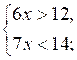
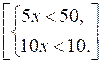
5. Решите систему неравенств:
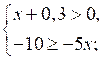
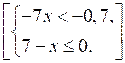
О т в е т ы:
В а р и а н т 1 [В а р и а н т 2]
1. Нет [нет].
2. (5; 6] [(5;9]].
3. (20;+∞) [{2}].
4. Нет решений [(–∞;1)].
5. [2;+∞) [[7;+∞)].