ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1026
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В а р и а н т 2
1. Изобразите на координатной плоскости множество решений неравенства:
а) у ≤ 1 – х; б) (х – 1)2 + у2 > 4.
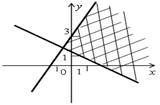
| 2. Задайте неравенством с двумя переменными множество точек заштрихованной области, изображенной на рисунке. | 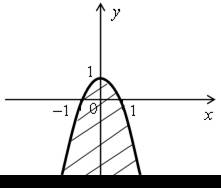 |
III. Объяснение нового материала.
На этом уроке следует изучить только решение систем линейных неравенств с двумя переменными, поскольку данная тема зачастую оказывается трудна для восприятия учащихся.
1. Рассмотреть несколько различных систем неравенств:
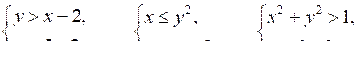
Взять пару чисел (1; 2) и проверить, является ли она решением этих систем.
2. Ввести понятие решения системы неравенств с двумя переменными.
3. Рассмотреть второй и третий примеры из учебника.
IV. Формирование умений и навыков.
Упражнения:
1. № 496.
2. № 497 (а, в).
3. Изобразите на координатной плоскости множество решений системы неравенств:
а) б)
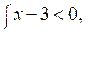 в)
в) 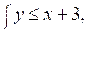
4. № 499 (а).
Сильным в учебе учащимся можно предложить дополнительно выполнить № 558.
Р е ш е н и е
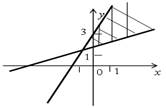
| Сначала изобразим множество решений первого неравенства системы: | 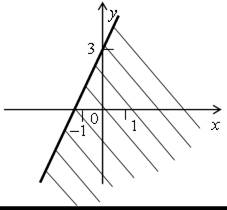 |
Чтобы система неравенств задавала на координатной плоскости полосу, необходимо выполнение двух условий:
1) прямая у = kх + b должна быть параллельна прямой у = 2х + 3, то есть k = 2;
2) прямая у = kх + b должна располагаться ниже прямой у = 2х + 3, то есть коэффициент b должен быть меньше 3, например: b = 0 или b = –2.
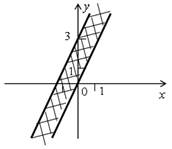
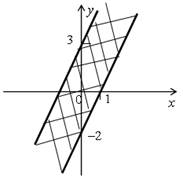
Чтобы данная система неравенств задавала на координатной плоскости угол, достаточно, чтобы прямая у = kх + b была непараллельна прямой у = 2х + 3, то есть k ≠ 2.
V. Итоги урока.
– Что называется решением системы неравенств с двумя переменными?
– Как решаются системы линейных неравенств с двумя переменными?
Домашнее задание: № 497 (б, г), № 498, № 499 (б).
У р о к 54 Дата:
РЕШЕНИЕ СИСТЕМ НЕРАВЕНСТВ ВТОРОЙ СТЕПЕНИ
С ДВУМЯ ПЕРЕМЕННЫМИ
Цель: формировать умение решать системы неравенств второй степени с двумя переменными.
Ход урока
I. Организационный момент.
II. Устная работа.
Является ли решением системы неравенств
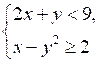 пара чисел:
пара чисел:а) (5; –3); б) (3; 1); в) (–1; 2)?
III. Объяснение нового материала.
Сначала необходимо актуализировать знания учащихся о решении систем линейных неравенств с двумя переменными, а затем разобрать пример 1 из учебника.
IV. Формирование умений и навыков.
Упражнения:
1. Изобразите на координатной плоскости множество решений системы:
а)
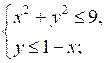 в)
в) 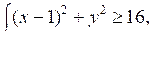
б)
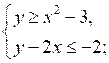 г)
г) 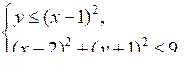
Р е ш е н и е
а)
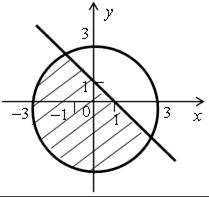 б)
б) 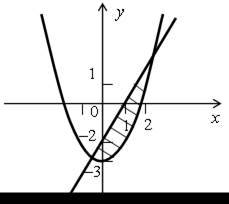
в)
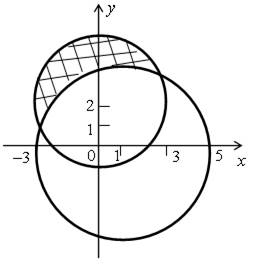 г)
г) 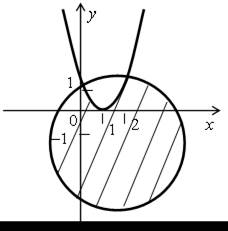
2. № 501 (а).
Р е ш е н и е
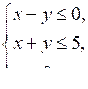 Изобразим на координатной плоскости множество решений этой системы, предварительно преобразовав ее: 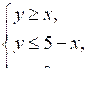 | 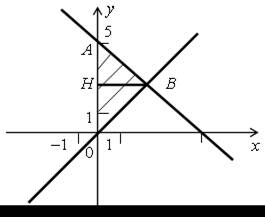 |
Таким образом, множество решений этой системы неравенств задает треугольник ОАВ. Для нахождения его площади нужно знать высоту ВН, то есть абсциссу точки В. Точка В является точкой пересечения прямых у = х и у = 5 – х. Решим уравнение:
х = 5 – х;
2х = 5;
х = 2,5.
Значит, в треугольнике ОАВ АО = 5 и ВН = 2,5.
S = ∙ AO ∙ BH;
S = ∙ 5 ∙ 2,5 = 6,25.
О т в е т: 6,25 ед2.
3. № 502 (б).
4. № 503.
Р е ш е н и е
Построим искомый угол:
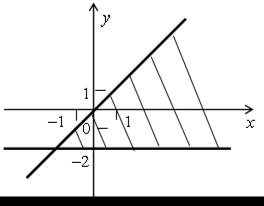
Получим систему неравенств:
Сильным в учебе учащимся можно предложить дополнительно выполнить несколько номеров.
1. № 577 (а).
Р е ш е н и е
| Неравенство х2 + у2 ≤ 25 задает круг с центром в начале координат и радиусом 5. Неравенство ху ≤ 0 задает вторую и четвертую координатные четверти. На рисунке показано множество решений этой системы неравенств: | 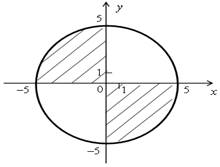 |
2. № 559 (б).
Р е ш е н и е
х (х2 – у) ≤ 0.
Произведение двух выражений будет отрицательным, если эти выражения имеют разные знаки. То есть это неравенство равносильно совокупности двух систем:
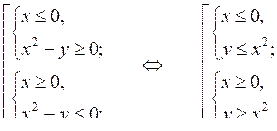
Изобразим на координатной плоскости множества решений каждой из систем:
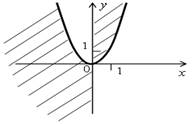
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что называется решением неравенства с двумя переменными?
– Что называется решением системы неравенств с двумя переменными?
– Как решаются неравенства с двумя переменными?
– Как решаются системы неравенств с двумя переменными?
Домашнее задание: № 500 (б, г), № 501 (б), № 502 (а).
У р о к 55 Дата:
ИТОГОВЫЙ УРОК ПО ТЕМЕ «УРАВНЕНИЯ
И НЕРАВЕНСТВА С ДВУМЯ ПЕРЕМЕННЫМИ»
Цели: обобщить и систематизировать знания учащихся по данной теме; закрепить умения решать уравнения, неравенства и их системы с двумя переменными.
Ход урока
I. Организационный момент.
II. Устная работа.
Какие из пар чисел (0; 3), (1; –2), (–1; 1) являются решениями данных систем?
а)
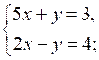 в)
в) 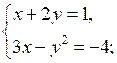
б)
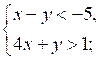 г)
г) 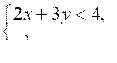
III. Формирование умений и навыков.
Предложить учащимся карточки-задания разного уровня сложности. Учащиеся выполняют решения самостоятельно, а учитель осуществляет контроль и в случае необходимости дает им консультации.
К а р т о ч к а № 1
1. Докажите, что пара чисел (–5; 2) не является решением системы уравнений
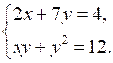
2. Решите систему уравнений:
а)
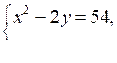 б)
б)
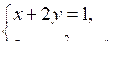
3. Сумма двух чисел равна 25, а их произведение равно 144. Найдите эти числа.
4. Изобразите на координатной плоскости множество решений системы неравенств:
а) б)