К а р т о ч к а  № 2

1. Решите систему уравнений:

а)                 б) 

2. Не выполняя построения, найдите координаты точек пересечения параболы у = 4х² – 2 и прямой 3х – 2у = –1.

3. Произведение двух чисел на 13 больше их суммы. Если из первого числа  вычесть  утроенное  второе  число,  то  получится  9.  Найдите  эти числа.

4. Изобразите на координатной плоскости множество решений системы неравенств:

а)                   б) 

 

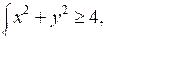
К а р т о ч к а  № 2

1. Решите систему уравнений:

а) 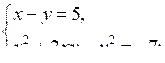                б)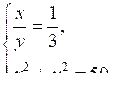 

2. Не выполняя построения, найдите координаты точек пересечения параболы у = 4х² – 2 и прямой 3х – 2у = –1.

3. Произведение двух чисел на 13 больше их суммы. Если из первого числа  вычесть  утроенное  второе  число,  то  получится  9.  Найдите  эти числа.

4. Изобразите на координатной плоскости множество решений системы неравенств:

а)                   б) 

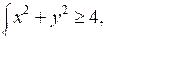
К а р т о ч к а  № 3*

1. Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют уравнению | у + 1 | = 2 – х.

2. Решите систему уравнений:

а) 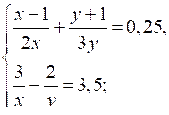               б)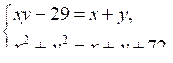 

3. При смешивании первого раствора кислоты, концентрация которого 20 %, и второго раствора этой же кислоты, концентрация которого 50 %, получили раствор, содержащий 30 % кислоты. В каком отношении были взяты первый и второй растворы?

4. При каких значения параметра а система уравнений:

 имеет два решения?

5. Изобразите на координатной плоскости множество решений системы неравенств:

---

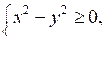
Р е ш е н и е  заданий карточки № 1

1. Подставим х = –5 и у = 2 в каждое из уравнений системы:

2 · (–5) + 7 · 2 = 4;

–10 + 14 = 4;

4 = 4 – верно.

–5 · 2 + 2² = 12;

–10 + 4 = 12;

–6 = 12 – неверно.

Значит, пара чисел (–5; 2) не является решением данной системы.

2.

а) 

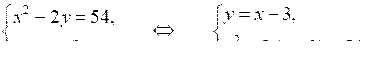
х² – 2х + 6 = 54;

х² – 2х – 48 = 0;

х₁ = –6      у₁ = –6 – 3 = –9;

х₂ = 8        у₂ = 8 – 3 = 5.

О т в е т: (–6; –9), (8; 5).

б) 

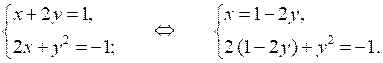
2 – 4у + у² = –1;

у² – 4у + 3 = 0;

у₁ = 1        х₁ = 1 – 2 · 1 = –1;

у₂ = 3        х₂ = 1 – 2 · 3 = –5.

О т в е т: (–1; 1), (–5; 3).

3. Обозначим первое число за х, а второе – за у. Согласно условию задачи получим систему уравнений:



25у – у² = 144;

у² – 25у + 144 = 0;

D = 625 – 4 · 144 = 49;

у₁ =   = 16          х₁ = 25 – 16 = 9;

у₂ =   = 9            х₂ = 25 – 9 = 16.

О т в е т: 9 и 16.

4.

а) 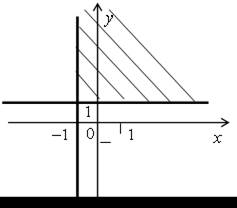          б)  

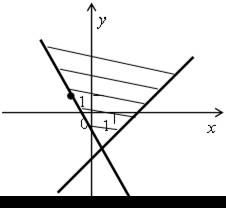
Р е ш е н и е  заданий карточки № 2

1. а) 

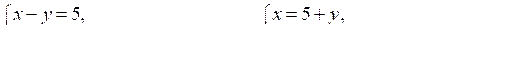
25 + 10у + у² + 10у + 2у² – у² = –7;

2у² + 20у + 32 = 0;

у² + 10у + 16 = 0;

у₁ = –2      х₁ = 5 + (–2) = 3;

у₂ = –8      х₂ = 5 + (–8) = –3.

О т в е т: (3; –2), (–3; –8).

б) 

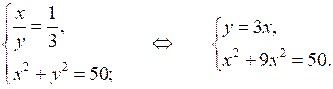
10х² = 50;

х² = 5;

х₁ =                у₁ = 3 ;

х₂ = –             у₂ = –3 .

О т в е т: ( ; 3 ), (– ; –3 ).

2. Чтобы найти координаты точек пересечения данных параболы и прямой, нужно решить систему уравнений:

3х – 8х² + 4 = –1;

8х² – 3х – 5 = 0;

х₁ = 1                  у₁ = 4 · 1 – 2 = 2;

---

х₂ =                у₂ = 4 ·   – 2 =  .

О т в е т: (1; 2),  .

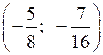3. Обозначим первое число за х, а второе – за у. Согласно условию задачи получим систему уравнений:

3у² + 9у = 4у + 22;

3у² + 5у – 22 = 0;

D = 25 + 264 = 289;

у₁ =   = 2          х₁ = 3 · 2 + 9 = 15;

у₂ = 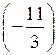       х₂ = 3 ·   + 9 = –2.

О т в е т: (15; 2),  .

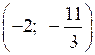4.

а) 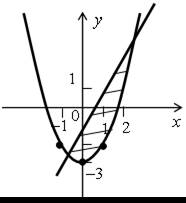                  б)  

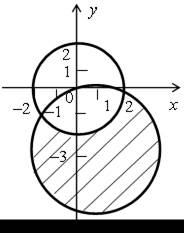
Р е ш е н и е  заданий карточки № 3*

1. Раскрывая модуль, получим совокупность двух уравнений:

1) если у ≥ –1, то      у + 1 = 2 – х,

                                 у = 1 – х;

2) если у < –1, то      –у – 1 = 2 – х,

                                 у = х – 3.

Изобразим на координатной плоскости оба этих случая:



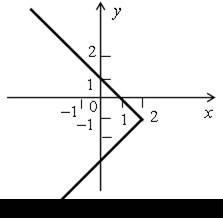
2.

а) 

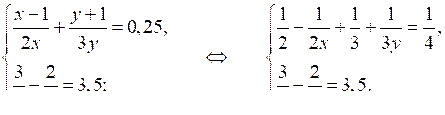
Сделаем замену:   = а,   = b. Получим систему:



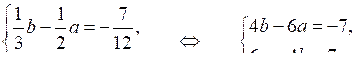
Складывая почленно левые и правые части уравнений этой системы, получим равенство:

0 = 0.

Значит, система имеет бесконечное множество решений.

Выразим из второго уравнения переменную а через переменную b:

6a – 4b = 7;

6a = 4b + 7;

a =  .

Возвращаясь к замене, получим:



Получаем, что исходная система имеет бесконечное множество решений вида  , где 

---

у ≠ 0 и у ≠  .

Например,  это  могут  быть  такие  пары,  как  , (2; –1), (1,2; –2). И т. д.

б) 

Обозначим х + у = т, а ху = п. Тогда имеем:

х²+ у² = (х + у)² – 2ху = т² – 2п. Получим систему:



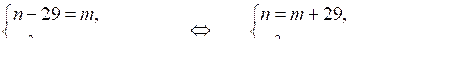
т² – 2т – 58 = т + 72;

т² – 3т – 130 = 0;

т₁ = –10    п₁ = –10 + 29 = 19;

т₂ = 13     п₂ = 13 + 29 = 42.

Возвращаясь к замене, получим системы:



Решая эти системы, получаем ответ.

О т в е т: (6; 7), (7; 6), (–5 +  ; –5 –  ), (–5 –  ; –5 +  ).

3. Пусть было взято x г первого раствора и y г – второго раствора. По условию в первом растворе было 0,2x г кислоты, а во втором – 0,5y г кислоты.

После  смешивания  получили  30 %-ный  раствор,  то  есть  в  нем  было 0,3 (x + y) г кислоты. Масса кислоты после смешивания двух растворов равна сумме масс исходных растворов.

Получим уравнение:

0,2x + 0,5y = 0,3(x + y);

0,2x + 0,5y = 0,3x + 0,3y;

0,2y = 0,1x;

2y = x.

Получаем,  что  первый  и  второй  растворы  были  взяты  в  отношении 2 : 1.

О т в е т: 2 : 1.

4. 

Вычтем почленно из второго уравнения системы первое:

2ху = 14 – 2 – 2а;

ху = 6 – а.

Тогда данную систему уравнений можно представить как совокупность двух систем:

1)                           2) 

Исходная система будет иметь два решения в трех случаях:

– если каждая из систем имеет по одному решению;

– если  первая  система  имеет  два  решения,  а  вторая – решений  не имеет;

– если  вторая  система  имеет  два  решения,  а  первая – решений  не имеет.

Если в каждой из полученных систем выразить одну переменную через другую и найти дискриминант, то в обоих случаях получим:

D = 4а – 10.

Выражение 4а – 10 не может быть одновременно больше и меньше нуля, поэтому подходит тот случай, когда каждая из систем имеет единственное решение, то есть, когда 

---

D = 0:

4а – 10 = 0;

а = 2,5.

О т в е т: 2,5.

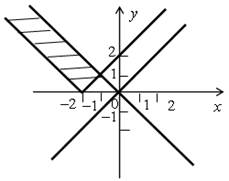
5. 

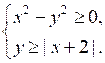
Для построения графика уравнения х² – у² = 0 воспользуемся формулой разности квадратов. Получим:

(х – у) (х + у) = 0

Для построения графика уравнения у = | х + 2 | необходимо раскрыть знак модуля и рассмотреть два случая.



Домашнее задание: № 527 (а, г), № 528 (а), № 529 (а), № 542, № 555.

 

 

 

 

У р о к  56                                                                  Дата:
КОНТРОЛЬНАЯ РАБОТА № 3

В а р и а н т  1

1. Решите систему уравнений:



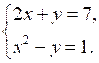
2. Периметр прямоугольника равен 28 м, а его площадь равна 40 м². Найдите стороны прямоугольника.

3. Не выполняя построения, найдите координаты точек пересечения параболы у = х² + 4 и прямой х + у = 6.

4. Решите систему уравнений:

5. Изобразите на координатной плоскости множество решений системы неравенств:



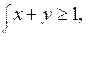
В а р и а н т  2

1. Решите систему уравнений:



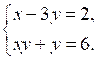
2. Одна из сторон прямоугольника на 2 см больше другой стороны. Найдите стороны прямоугольника, если его площадь равна 120 см².

3. Не выполняя построения, найдите координаты точек пересечения окружности х² + у² = 10 и прямой х + 2у = 5.

4. Решите систему уравнений:

5. Изобразите на координатной плоскости множество решений системы неравенств:



 

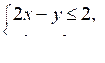
Домашнее задание:  решить другой вариант

 

 

 

 

 

В а р и а н т  3

1. Решите систему уравнений:

2. Периметр прямоугольника равен 26 см, а его площадь равна 42 см

---

Смотрите также файлы

• Отчёт по слесарной практике.docx

• В таблице представлены данные о полезности товара А. Определите среднюю и предельную полезность единицы товара А.docx

• Мишель де монтень Насретдинова П. Д., 329 группа.pptx

• 1. Контакт глазами.docx

• Реферат по дисциплине на тему Экология и здоровье человека.docx