Файл: Учебнометодическое пособие для направлений подготовки 44. 03. 01 Педагогическое образование и 44. 03. 05 Педагогическое образование (с двумя профилями подготовки).docx

ЛАБОРАТОРНАЯ РАБОТА № 11

Определение момента инерции методом трифелярного подвеса. Проверка теоремы Штейнера

Цель работы: изучение свойств момента инерции; определение момента инерции с помощью трифелярного подвеса; проверка теоремы о параллельных осях (теорема Штейнера).

Приборы и принадлежности: трифелярный подвес, механический секундомер (предел точности 0,2 с), штангенциркуль (предел точности 0,05 мм), масштабная линейка, транспортир, цилиндрические грузы различной массы.

В ведение

Трифелярный подвес (Рис. 1) представляет собой круглую массивную (М=4,25 кг) платформу 1, подвешенную на трех симметрично расположенных нитях 2 одинаковой длины (длина нитей l для каждого трифелярного подвеса измеряется самостоятельно), закрепленных у края этой платформы. Вверху эти нити также симметрично прикреплены к краю диска 3, имеющего несколько меньший диаметр, чем диаметр платформы. Платформа способна совершать малые крутильные колебания около вертикальной оси, перпендикулярной к ее плоскости и проходящей через середину; центр тяжести платформы при этом перемещается вдоль оси вращения.

Период колебания платформы определяется величиной ее момента инерции. Но если нагрузить платформу каким-либо телом, то период колебаний системы изменится; этим обстоятельством и пользуются в данной лабораторной работе.

Если платформа массы M, вращаясь в одном направлении, поднялась на высоту h, то приращение потенциальной энергии будет равно:

E₁=Mgh,

где g – ускорение силы тяжести.

Вращаясь в противоположном направлении, платформа придет в положение равновесия с кинетической энергией, равной:

,

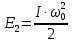где I – момент инерции платформы, 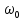– угловая скорость платформы в момент достижения ею положения равновесия.

---

Пренебрегая работой сил трения, на основании закона сохранения механической энергии имеем:

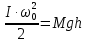. (1)

Считая, что платформа совершает малые гармонические колебания, можем записать зависимость углового смещения платформы от времени в виде:

,

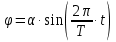где  – угловое смещение платформы,  – амплитуда смещения, T – период колебания, t – время.

Угловая скорость, являющаяся первой производной от углового смещения по времени, выражается следующим образом:

.

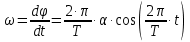В момент прохождения через положение равновесия абсолютное значение этой величины будет равно:

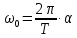. (2)

На основании выражений (1) и (2) имеем:

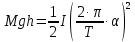. (3)

Пусть l – длина нитей подвеса, R=163,510^-3 м– расстояние от центра платформы до точек крепления нитей (радиус платформы), r=410^-2 м – радиус верхнего диска.

Из Рис. 2:



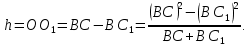
Так как

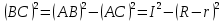, а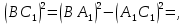





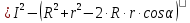
то

= .

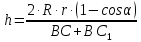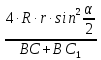При малом угле отклонения , значение синуса этого угла можно заменить значением самого , а величину знаменателя положить равной 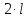(объяснить почему?).

Учитывая это, получаем:

.

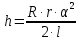Подставив данное выражение в формулу (3) получим:

.

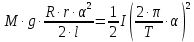Откуда

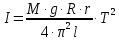. (4)

Таким образом, по формуле (4) может быть определен момент инерции, как самой платформы, так и системы, представляющей собой платформу с нагруженными на нее телами.

---

Вращательный импульс, необходимый для начала крутильных колебаний, сообщается платформе путем поворота верхнего диска вокруг вертикальной оси при помощи натяжения шнура 4, приводящего в движение рычажок 5, связанный с диском. Этим достигается почти полное отсутствие других, некрутильных, колебаний. Для удобства отсчета колебаний на платформе имеется метка, против которой при покоящейся платформе устанавливается указатель 6.

Порядок выполнения работы

Задание № 1. Определение момента инерции I_п пустой (ненагруженной) платформы.

С помощью транспортира отметьте малый ( 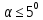– почему?) угол поворота платформы. Измерьте с точностью до 0,5 см длину нитей l. Определите цену деления механического секундомера (внимание: самостоятельно выявить систематическую ошибку секундомера; если таковая существует – учитывать ее при измерениях). Осторожно потянув за шнур 4, придайте платформе малые крутильные колебания (внимание: при этом следите, чтобы колебания платформы происходили только вокруг вертикальной оси, проходящей через середины платформы и верхнего диска). При помощи механического секундомера определяют время t n=30-50 полных колебаний, а затем вычисляют время (период) одного полного колебания. Подставив все известные, а также измеренные величины в формулу (4) определяют момент инерции I_п пустой платформы.

Примечание. Измерение времени t n=30-50 полных колебаний провести три раза, после чего вычислить периоды колебаний и взять их среднее арифметическое значение. Результаты измерений занести в таблицу.

№	n	l, м	t, с	T, с		Iп, кгм2
1
2
3

---

Задание № 2. Определение момента инерции колебательной системы (платформа с нагруженными на нее телами).

Выберите два совершенно одинаковых груза m.

1. 
   Расположите один груза в центре платформы и определите момент инерции системы I_1ц (смотрите Задание № 1).
   
2. 
   Расположите оба груза (Рис. 3а) в центре платформы и определите момент инерции системы I_2ц (смотрите Задание № 1).
   
3. 
   Расположите оба груза диаметрально противоположно во вторых (от центра) отверстиях на платформе и определите момент инерции системы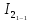 (смотрите Задание № 1).
   
4. 
   Расположите оба груза (Рис. 3б) диаметрально противоположно во вторых (от центра) отверстиях на платформе и определите момент инерции системы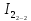 (смотрите Задание № 1).
   
5. 
   Расположите оба груза (Рис. 3в) диаметрально противоположно в третьих (от центра) отверстиях на платформе и определите момент инерции системы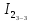 (смотрите Задание № 1).
   

Обратите внимание, что при подстановке данных в расчетную формулу (4) общая масса системы складывается из массы платформы M и массы грузов m.

Внимание: следите, чтобы колебания платформы происходили только вокруг вертикальной оси, проходящей через середины платформы и верхнего диска.

Примечание. Измерение времени t n=30-50 полных колебаний провести для каждого расположения грузов на платформе также по три раза, после чего вычислить периоды колебаний и взять их среднее арифметическое значение. Результаты измерений занести в таблицы (3 таблицы).

№	n	m, кг	l, м	t, с	T, с		I1ц, кгм2
1
2
3

---

№	n	m, кг	l, м	t, с	T, с		I2ц, кгм2
1
2
3

№	n	m, кг	l, м	t, с	T, с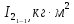
1
2
3

№	n	m, кг	l, м	t, с	T, с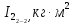
1
2
3

№	n	m, кг	l, м	t, с	T, с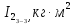
1
2
3

---