Файл: Методическое пособие по дисциплине методы оптимальных решений 1 семестр Направление подготовки 080100 Экономика.doc

стоит в 4-й строке столбца вектора Р₃. Следовательно, в базис введем вектор Р₃. определяем вектор, подлежащий исключению из базиса. Для этого находим для , т. е.

Найдя число мы тем самым с экономической точки зрения определили, какое количество изделий С предприятие может изготовлять с учетом норм расхода и имеющихся объемов сырья каждого вида. Так как сырья данного вида соответственно имеется 360, 192 и 180 кг, а на одно изделие С требуется затратить сырья каждого вида соответственно 12, 8 и 3 кг, то максимальное число изделий С, которое может быть изготовлено предприятием, равно т. е. ограничивающим фактором для производства изделий С является имеющийся объем сырья II вида. С учетом его наличия предприятие может изготовить 24 изделия С. При этом сырье II вида будет полностью использовано.

Следовательно, вектор Р₅ подлежит исключению из базиса. Столбец вектора Р₃к 2-я строка являются направляющими. Составляем таблицу для II итерации (таблица 7).

Таблица 7

i	Базис	Сб	Р0	9	10	16	0	0	0
				P1	P2	P3	p4	p5	Р6
1 2 3 4	P4 p3 p6	0 16 0	72 24 108 384	9 3/4 11/4 3	9 1/2 3/2 -2	0 1 0 0	1 0 0 0	-3/2 1/8 -3/8 2	0 0 1 0

---

Сначала заполняем строку вектора, вновь введенного в базис, т. е. строку, номер которой совпадает с номером направляющей строки. Здесь направляющей является 2-я строка. Элементы этой строки таблицы 7 получаются из соответствующих элементов таблицы 6 делением их на разрешающий элемент (т. е. на 8). При этом в столбце С_б записываем коэффициент , стоящий в столбце вводимого в базис вектора . Затем заполняем элементы столбцов для векторов, входящих в новый базис. В этих столбцах на пересечении строк и столбцов одноименных векторов проставляем единицы, а все остальные элементы полагаем равными нулю.

Для определения остальных элементов таблицы 7 применяем правило треугольника. Эти элементы могут быть вычислены и непосредственно по рекуррентным формулам.

Вычислим элементы таблицы 7, стоящие в столбце вектора Р₀. Первый из них находится в 1-й строке этого столбца. Для его вычисления находим три числа:

1) число, стоящее в таблице 6 на пересечении столбца вектора Р₀ и 1-й строки (360);

2) число, стоящее в таблице 6 на пересечении столбца вектора P₃ и 1-й строки (12);

3) число, стоящее в таблице 7 на пересечении столбца вектора Р₀ и 2-й строки (24).

Вычитая из первого числа произведение двух других, находим искомый элемент: 360 – 12  24=72; записываем его в 1-й строке столбца вектора Р₀ таблице 7.

Второй элемент столбца вектора Р₀ таблицы 7 был уже вычислен ранее. Для вычисления третьего элемента столбца вектора Р₀ также находим три числа. Первое из них (180) находится на пересечении 3-й строки и столбца вектора Р₀ таблицы 6, второе (3) — на пересечении 3-й строки и столбца вектора P₃ таблицы 6, третье (24) — на пересечении 2-й строки и столбца вектора Р₀ таблицы 8. Итак, указанный элемент есть 180 – 24  3=108. Число 108 записываем в 3-й строке столбца вектора Р₀таблицы 7.

Значение F₀ в 4-й строке столбца этого же вектора можно найти двумя способами:

1) по формуле , т.е.

2) по правилу треугольника; в данном случае треугольник образован числами 0, -16, 24. Этот способ приводит к тому же результату: 0 - (-16)  24=384.

---

При определении по правилу треугольника элементов столбца вектора Р₀ третье число, стоящее в нижней вершине треугольника, все время оставалось неизменным и менялись лишь первые два числа. Учтем это при нахождении элементов столбца вектора P₁ таблицы 7. Для вычисления указанных элементов первые два числа берем из столбцов векторов P₁ и Р₃ таблицы 6, а третье число — из таблицы 7. Это число стоит на пересечении 2-й строки и столбца вектора P₁ последней таблицы. В результате получаем значения искомых элементов: 18 – 12  (3/4) =9; 5 – 3  (3/4) = 11/4.

Число в 4-й строке столбца вектора P₁ таблицы 7 можно найти двумя способами:

1) по формуле имеем

2) по правилу треугольника получим

Аналогично находим элементы столбца вектора P₂.

Элементы столбца вектора Р₅ вычисляем по правилу треугольника. Однако построенные для определения этих элементов треугольники выглядят иначе.

При вычислении элемента 1-й строки указанного столбца получается треугольник, образованный числами 0,12 и 1/8. Следовательно, искомый элемент равен 0 – 12  (1/8) = -3/2. Элемент, стоящий в 3-й строке данного столбца, равен 0 - 3  (1 /8) = -3/8.

По окончании расчета всех элементов таблицы 7 в ней получены новый опорный план и коэффициенты разложения векторов через базисные векторы и значения и . Как видно из этой таблицы, новым опорным планом задачи является план X=(0; 0; 24; 72; 0; 108). При данном плане производства изготовляется 24 изделия С и остается неиспользованным 72 кг сырья 1 вида и 108 кг сырья III вида. Стоимость всей производимой при этом плане продукции равна 384 руб. Указанные числа записаны в столбце вектора Р₀ таблицы 7. Как видно, данные этого столбца по-прежнему представляют собой параметры рассматриваемой задачи, хотя они претерпели значительные изменения. Изменились данные и других столбцов, а их экономическое содержание стало более сложным. Так, например, возьмем данные столбца вектора

---

Р₂. Число 1/2 во 2-й строке этого столбца показывает, на сколько следует уменьшить изготовление изделий С, если запланировать выпуск одного изделия В. Числа 9 и 3/2 в 1-й и 3-й строках вектора P₂ показывают соответственно, сколько потребуется сырья I и II вида при включении в план производства одного изделия В, а число — 2 в 4-й строке показывает, что если будет запланирован выпуск одного изделия В, то это обеспечит увеличение выпуска продукции в стоимостном выражении на 2 руб. Иными словами, если включить в план производства продукции одно изделие В, то это потребует уменьшения выпуска изделия С на 1/2 ед. и потребует дополнительных затрат 9 кг сырья I вида и 3/2 кг сырья III вида, а общая стоимость изготовляемой продукции в соответствии с новым оптимальным планом возрастет на 2 руб. Таким образом, числа 9 и 3/2 выступают как бы новыми «нормами» затрат сырья I и III вида на изготовление одного изделия В (как видно из таблицы 6, ранее они были равны 15 и 3), что объясняется уменьшением выпуска изделий С.

Такой же экономический смысл имеют и данные столбца вектора Р₁ таблицы 7. Несколько иное экономическое содержание имеют числа, записанные в столбце вектора Р₅. Число 1/8 во 2-й строке этого столбца, показывает, что увеличение объемов сырья II вида на 1 кг позволило бы увеличить выпуск изделий С на 1/8 ед. Одновременно потребовалось бы дополнительно 3/2 кг сырья I вида и 3/8 кг сырья III вида. Увеличение выпуска изделий С на 1/8 ед. приведет к росту выпуска продукции на 2 руб.

Из изложенного выше экономического содержания данных таблицы 7 следует, что найденный на II итерации план задачи не является оптимальным. Это видно и из 4-й строки таблицы 7, поскольку в столбце вектора P₂ этой строки стоит отрицательное число — 2. Значит, в базис следует ввести вектор P₂, т. е. вновом плане следует предусмотреть выпуск изделий В. При определении возможного числа изготовления изделий В следует учитывать имеющееся количество сырья каждого вида, а именно: возможный выпуск изделий В определяется 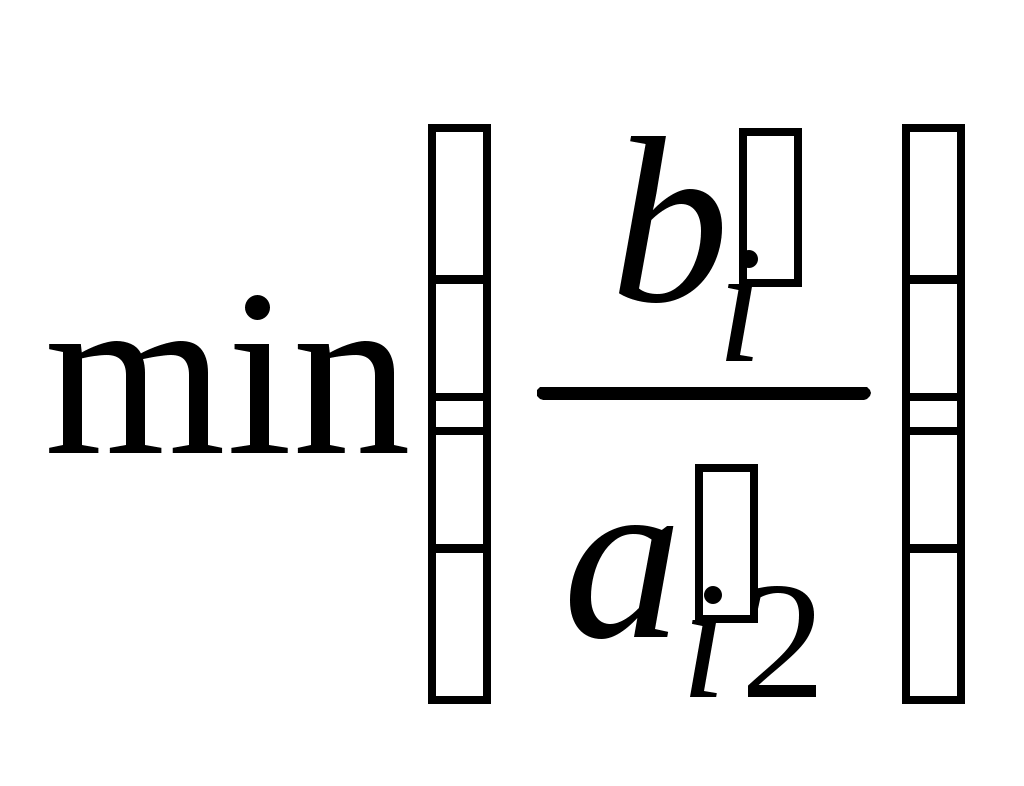для , т. е. находим

---

Следовательно, исключению из базиса подлежит вектор Р₄иными словами, выпуск изделий В ограничен имеющимся в распоряжении предприятия сырьем I вида. С учетом имеющихся объемов этого сырья предприятию следует изготовить 8 изделий В. Число 9 является разрешающим элементом, а столбец вектора P₂ и 1-я строка таблицы 7 являются направляющими. Составляем таблицу для III итерации (таблица 8).

Таблица 8

i	Базис	Сб	P0	9	10	16	0	0	0
				P1	P2	P3	p4	p5	Р6
1 2 3 4	P2 P3 Р6	10 16 0	8 20 96 400	1 1/4 5/4 5	1 0 0 0	0 1 0 0	1/9 -1/18 -1/6 2/9	-1/6 5/24 -1/8 5/3	0 0 1 0

В таблице 8 сначала заполняем элементы 1-й строки, которая представляет собой строку вновь вводимого в базис вектора Р₂. Элементы этой строки получаем из элементов 1-й строки таблицы 7 делением последних на разрешающий элемент (т.е. на 9). При этом в столбце С_б данной строки записываем .

Затем заполняем элементы столбцов векторов базиса и по правилу треугольника вычисляем элементы остальных столбцов. В результате в таблице 8 получаем новый опорный план X=(0; 8; 20; 0; 0; 96) и коэффициенты разложения векторов через базисные векторы и соответствующие значения и

---