ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 395
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Рисунок 4 – Схема закрепления кольца с некруглой
Рисунок 17--Схема образования погрешности закрепления
Поэтому и для технологической системы необходимо, чтобы
3.5.3 Задание к лабораторной работе
3.5.5 Методика и порядок выполнения лабораторной работы
4. Проников А.С. Надёжность машин. М. Маш. 1978. 591с.
5. Когаев В.П., Дроздов Ю.Н. прочность и износостойкость деталей машин. М. ВШ.1991.319с.
6. Аристов А.В. управление качеством. М. Инфра М. 2000. 238с.
3.6.2.2 Погрешности, связанные с тепловыми деформациями технологических систем
угловое перемещение сечения В от внешней силы Р в направлении этой силы;
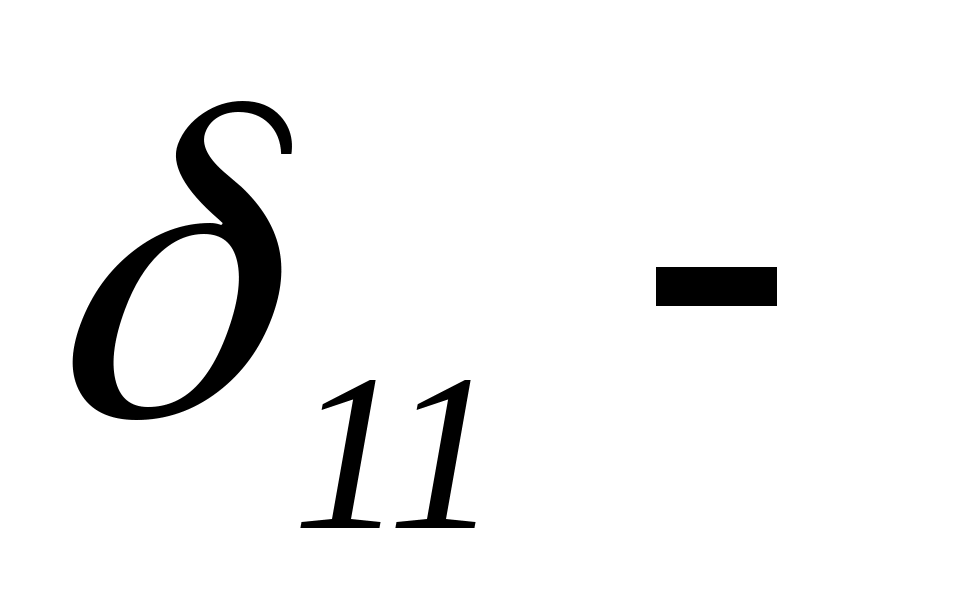 угловое перемещение сечения В от единичного момента, приложенного в сечении В, в направлении действия внутреннего момента M;
угловое перемещение сечения В от единичного момента, приложенного в сечении В, в направлении действия внутреннего момента M;
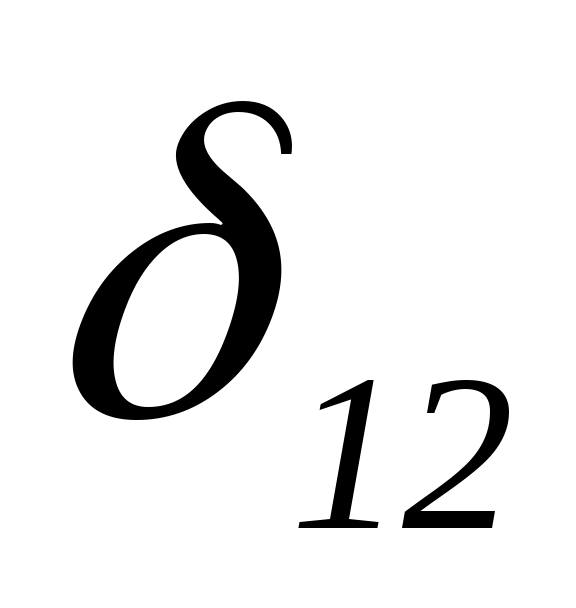 – угловое перемещение сечения В от единичной силы, приложенной в направлении силы N.
– угловое перемещение сечения В от единичной силы, приложенной в направлении силы N.
Аналогично для второго уравнения каждое из слагаемых представляет собой линейное перемещение сечения В в направлении силы N от заданной нагрузки Р (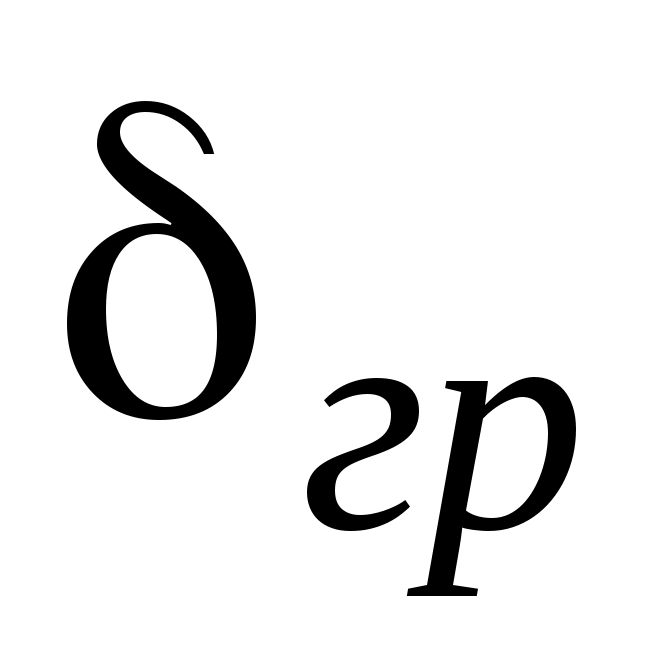 ), внутреннего изгибающего момента М(
), внутреннего изгибающего момента М(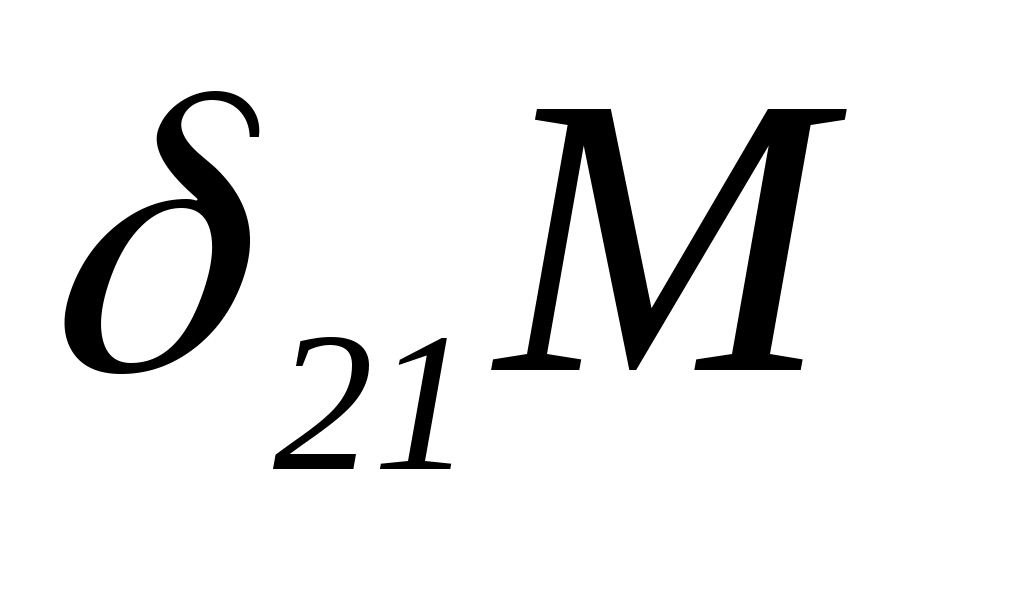 ) и нормальной силы
) и нормальной силы 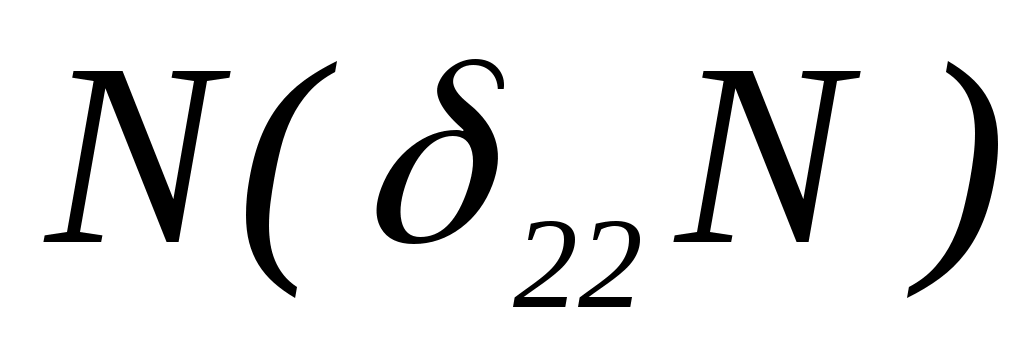 . Для каждого из участков, показанных на рисунке 5 римскими цифрами, можно составить уравнения моментов. Перемещения для решения канонических уравнений определяются с помощью интеграла Мора:
. Для каждого из участков, показанных на рисунке 5 римскими цифрами, можно составить уравнения моментов. Перемещения для решения канонических уравнений определяются с помощью интеграла Мора:
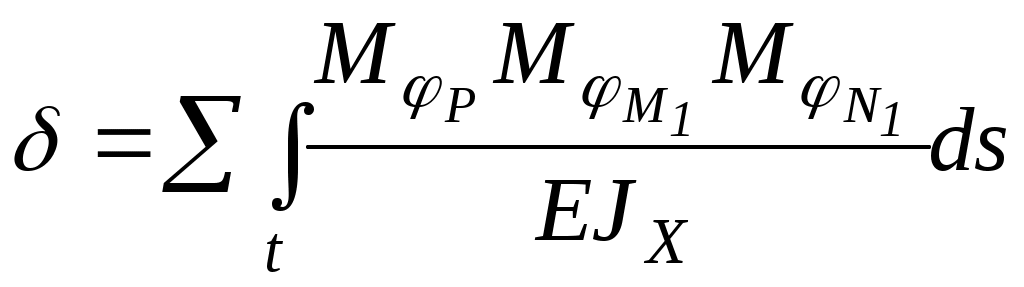 ,
,
где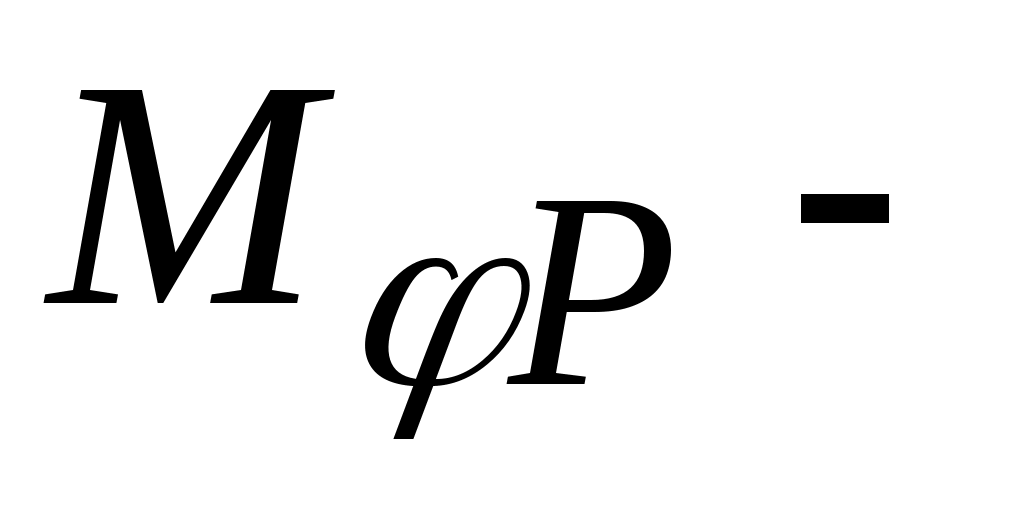 момент в текущем сечении от заданной нагрузки;
момент в текущем сечении от заданной нагрузки;
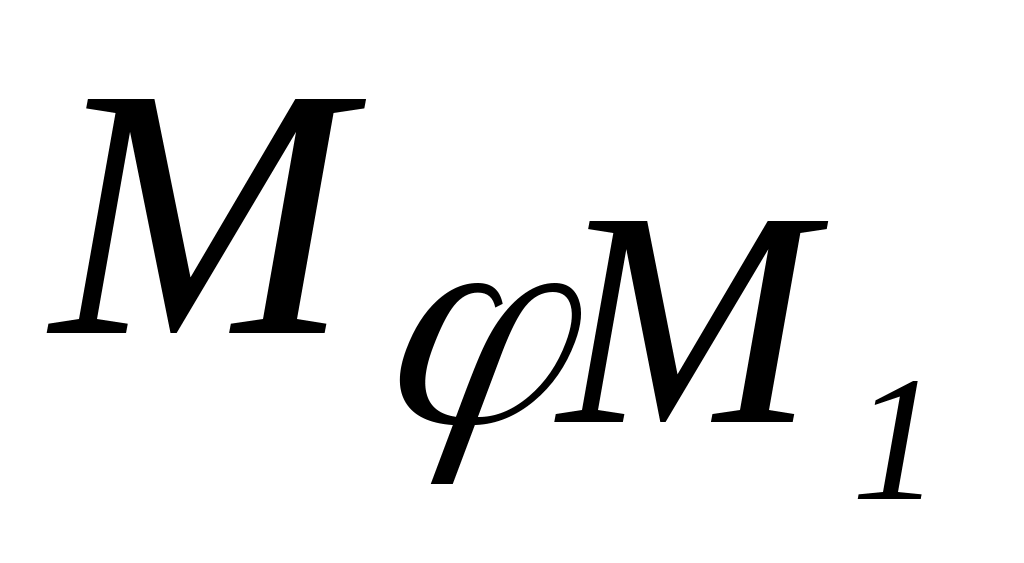 – момент в текущем сечении от единичного момента,
– момент в текущем сечении от единичного момента,
приложенного в направлении неизвестного момента M,
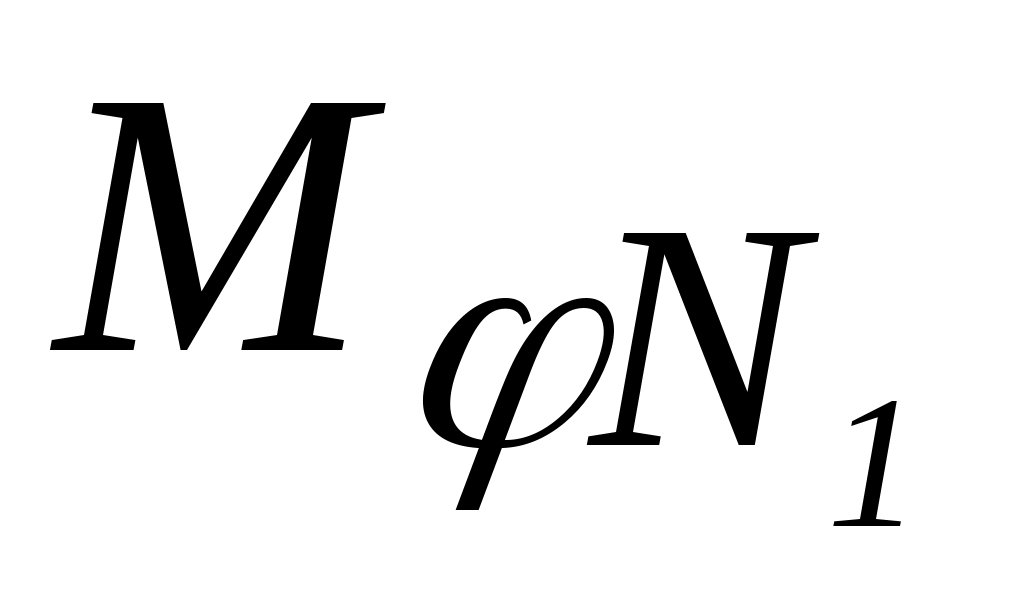 – момент в текущем сечении от единичной силы, приложенной в направлении неизвестной силы N.
– момент в текущем сечении от единичной силы, приложенной в направлении неизвестной силы N.
Например,
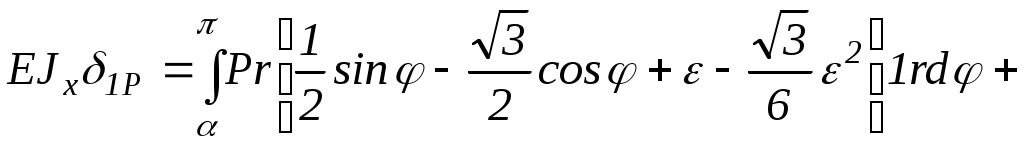
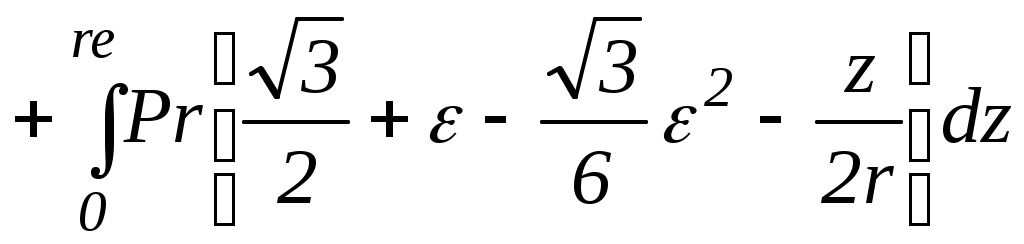
а после некоторых преобразований
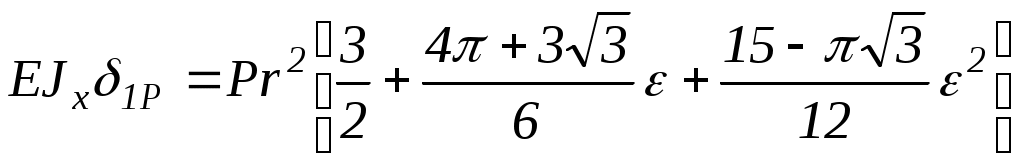
Если ε <0,1 (в большинстве случаев чистовой обработки имеем 0< ε <0,1), то ошибка, вызванная пренебрежением последнего члена, будет меньше 0,53%. Аналогичным методом находим EJxδ2P, EJxδ11, EJxδ22, EJxδ12, EJxδ21. Таким образом, канонические уравнения метода сил принимают вид
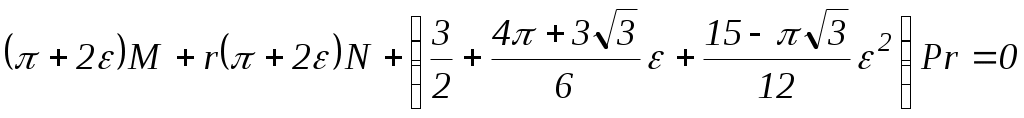
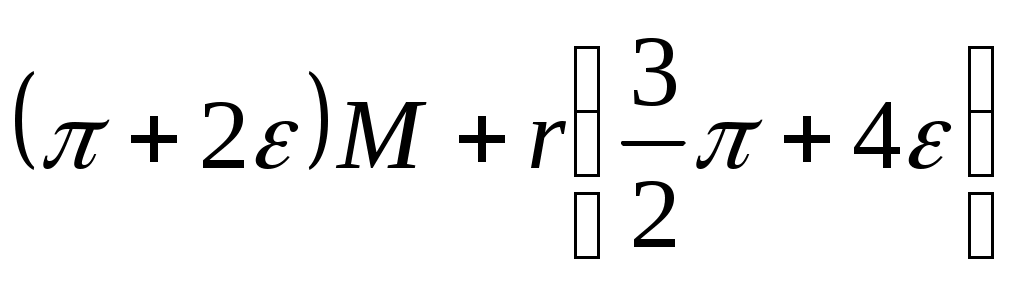
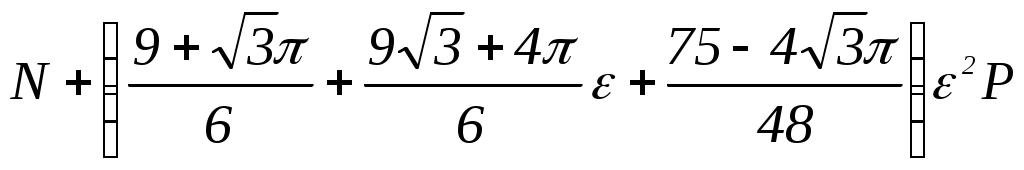
Решение уравнений дает

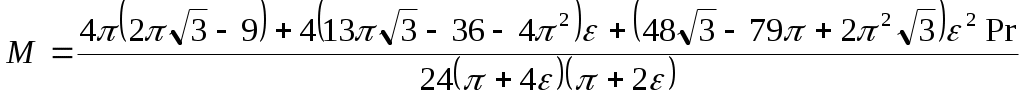
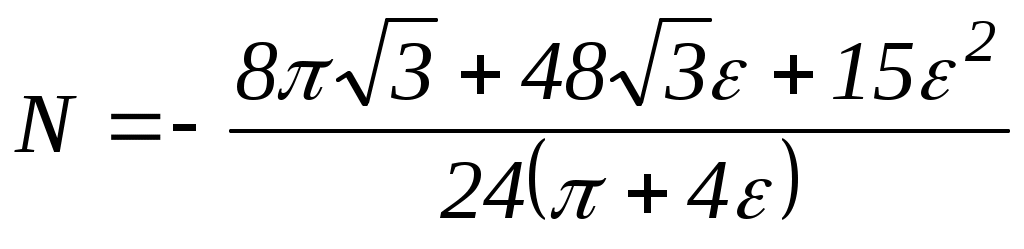
Если в последних формулах положить ε = 0, то получим известное решение M ≈ 0.1Pr; N = –0.577P. Для определения перемещений предварительно находят выражения изгибающих моментов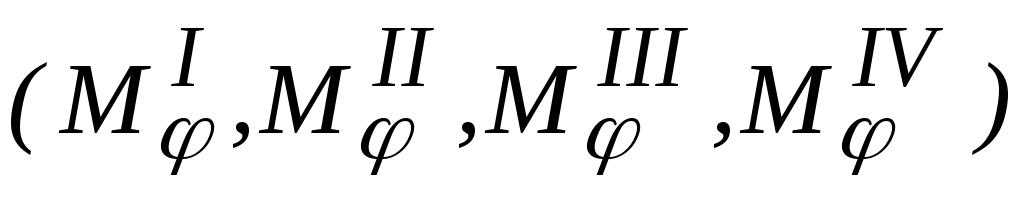 для каждого сечения, а также уравнения моментов от единичных нагрузок
для каждого сечения, а также уравнения моментов от единичных нагрузок 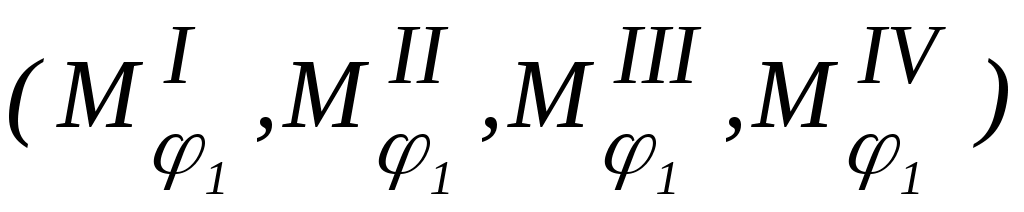 . Например, горизонтальное смещение точки С (рисунок 5) можно определить как
. Например, горизонтальное смещение точки С (рисунок 5) можно определить как
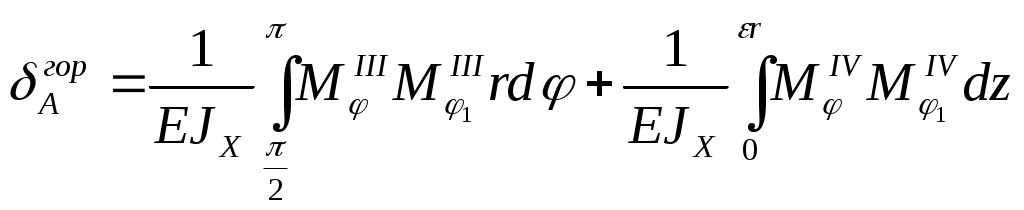
Для приведения уравнений, полученных с помощью данной методики, к виду, удобному для практического пользования, необходимо сделать ряд преобразований. Приведенные ранее значения М и N представим в виде
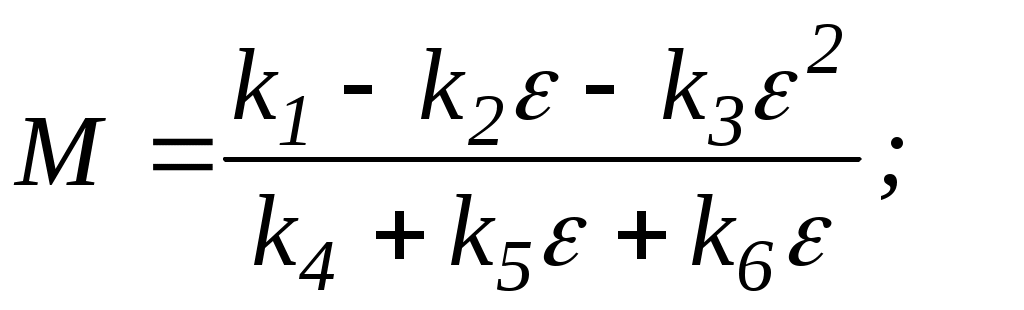
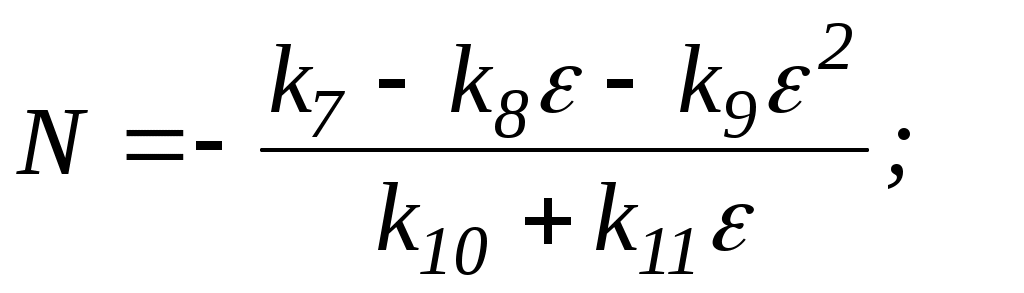
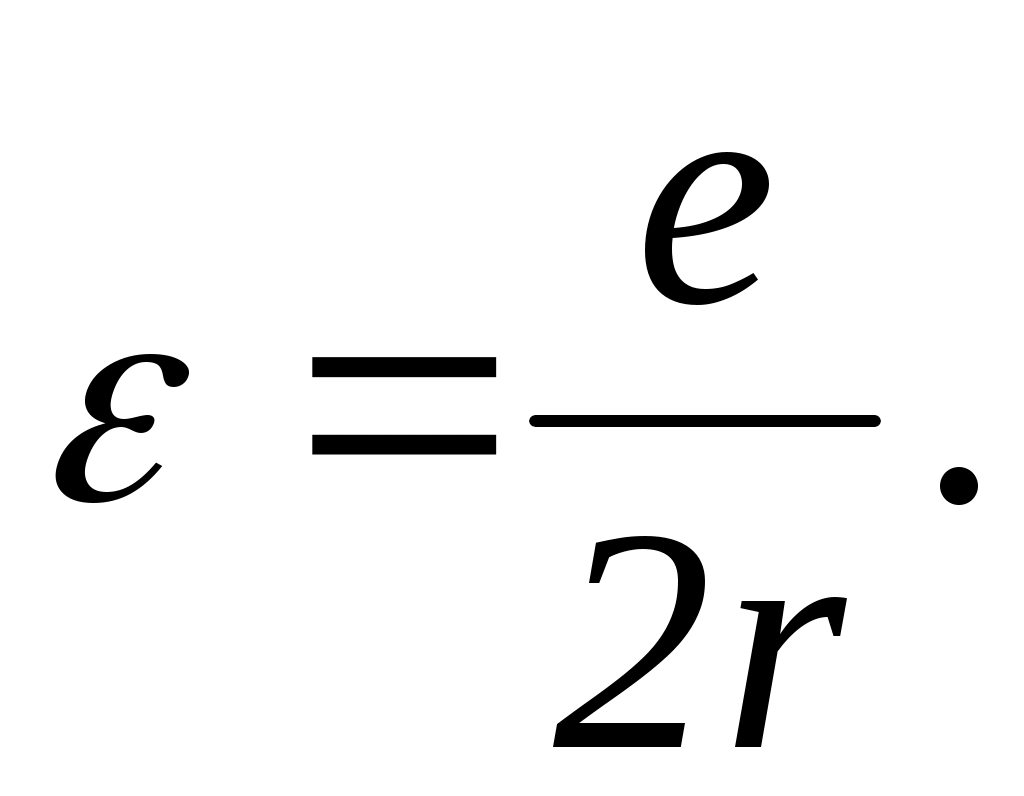
Значения коэффициентов k1– k11 следующие: k1= 23,66;
k2= 19,2816; k3= 130,8643; k4= 237,87; k5= 452,367; k6= 192,0; k7= =43,5296; k8= 83,136; k9=15,0; k10= 75,3978; k11= 96,0.
Аналогично, произведя преобразования, можно определять суммарное перемещение под тремя кулачками, закрепляющими некруглое кольцо:
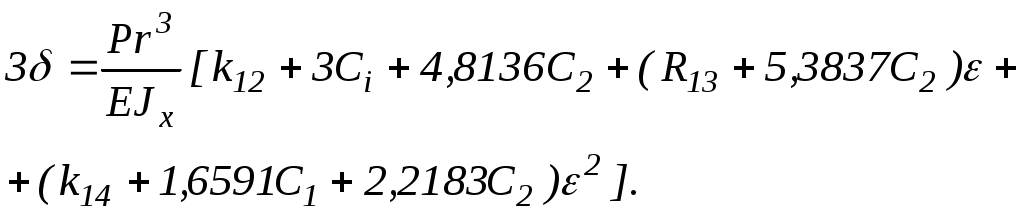
Здесь значения k12=2,5273; k13=2,50; k14=5,4877. Коэффициенты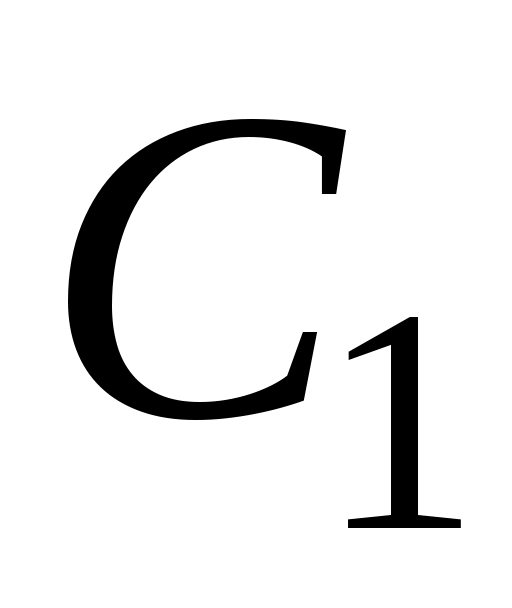 и
и 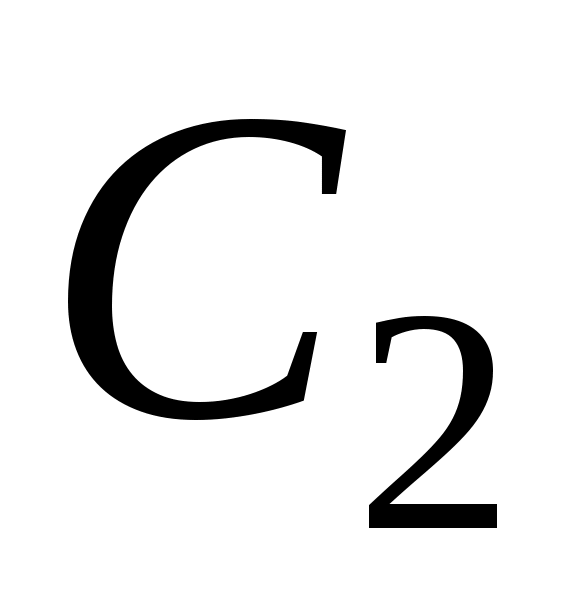 являются функцией ε. Для ε = 0,05
являются функцией ε. Для ε = 0,05 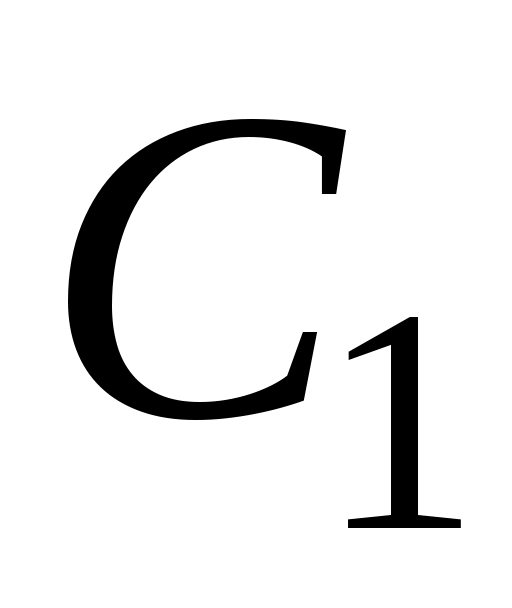
= 0,082; = 0,6. Использование указанных формул становится тем рациональнее, чем больше овальность установочной базы.
= 0,6. Использование указанных формул становится тем рациональнее, чем больше овальность установочной базы.
Зажимные устройства способны создавать отклонения формы на заготовках и деталях, которые до закрепления таких отклонений не имели. Поэтому можно считать, что в этих случаях зажимные устройства порождают погрешность формы. Допустим, что высокоточную гильзу закрепляют в двух местах с базированием по отверстию двумя гофрированными втулками (см. рисунок 2,г) для проведения шлифования. Зажимное приспособление создает осесимметричное нагружение; нагрузка распределенная. При снятии сил закрепления после обработки деформация гильзы исчезает. Это приводит к искажению формы обработанной поверхности. В связи с этим возникает необходимость оценки величины деформации, вызванной силами закрепления.
Возможно решение обратной задачи: определение такой силы закрепления, которая вызывала бы допустимую деформацию. Искажения формы закрепляемых гильз могут быть определены на основе теории осесимметричной деформации цилиндрических оболочек. В общем случае высокоточная гильза может быть представлена состоящей из отдельных участков в зависимости от геометрических параметров и характера нагружения. Действие одного участка на другой заменяется изгибающим моментом М и поперечной силой Q. Обозначим все величины, относящиеся к началу i-го участка, индексом: 1, а к концу – индексом i2. Радиусы срединной поверхности i-го и i+1-го участков могут быть различными и равными соответственно r1 и ri+1 Силовые факторы в конце предыдущего и в начале следующего участков связаны между собой следующими зависимостями:

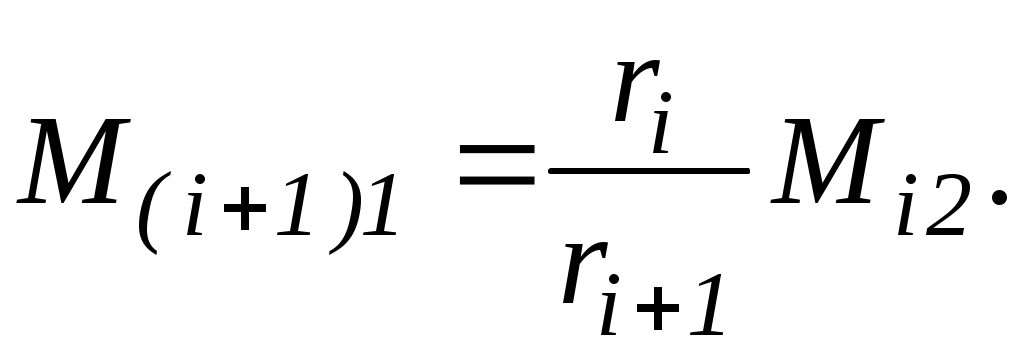
Для коротких участков гильзы выражения для радиального перемещения W, угла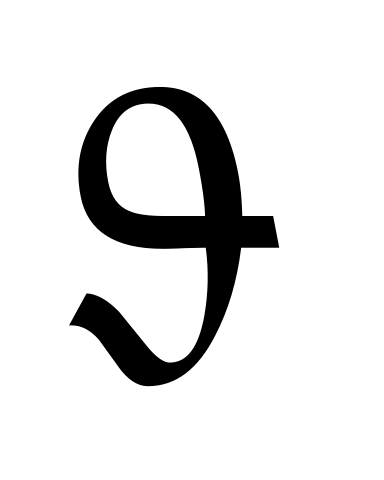 поворота нормалей, изгибающего момента
поворота нормалей, изгибающего момента 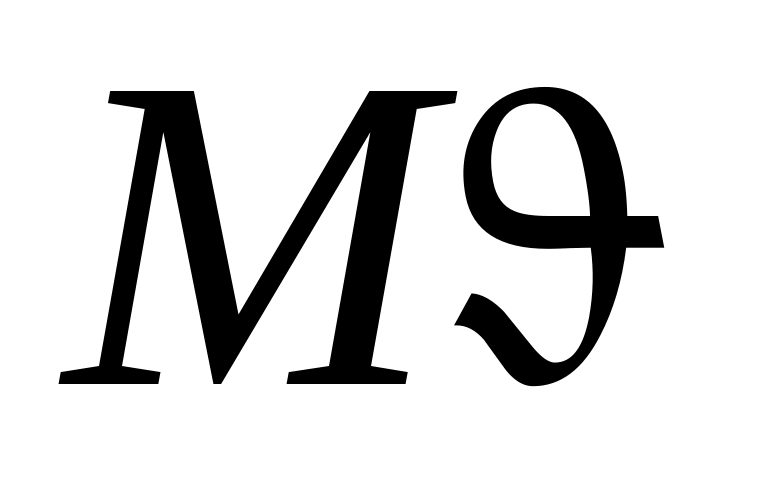 и поперечной силы Q записываются в функциях Крылова:
и поперечной силы Q записываются в функциях Крылова:
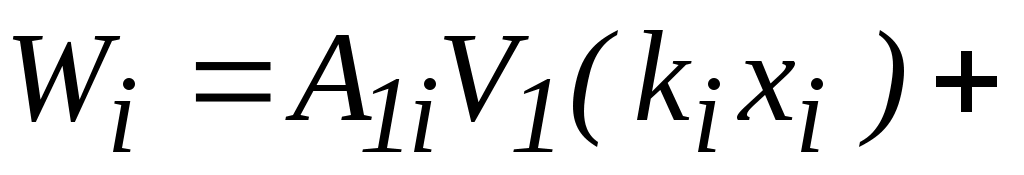
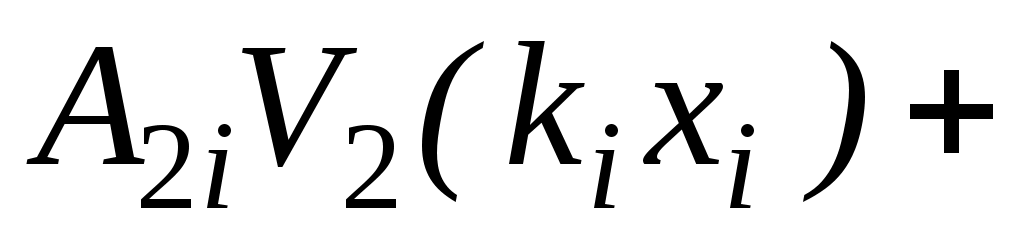
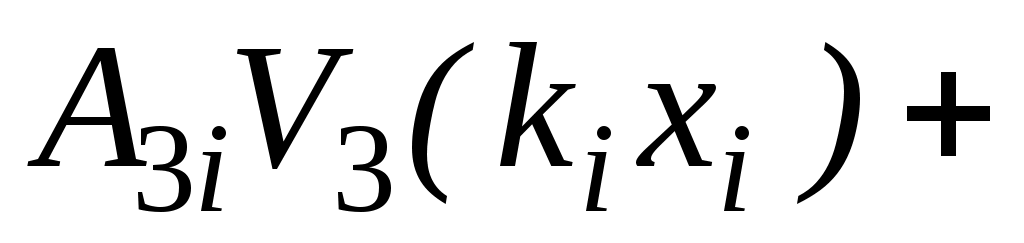
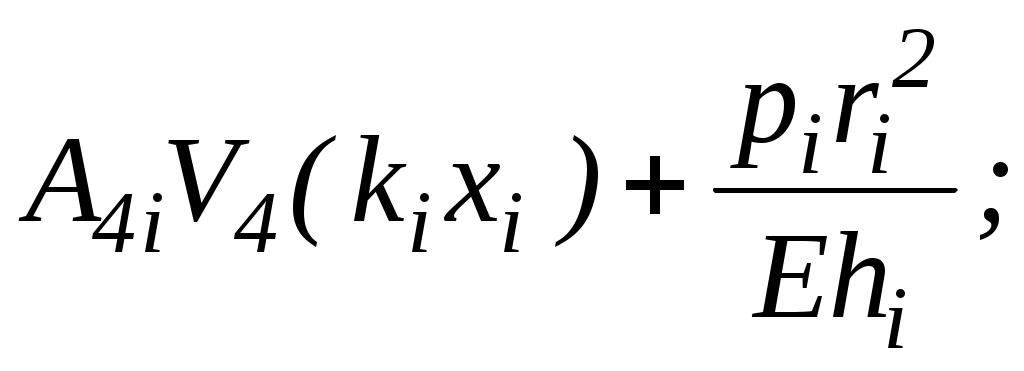
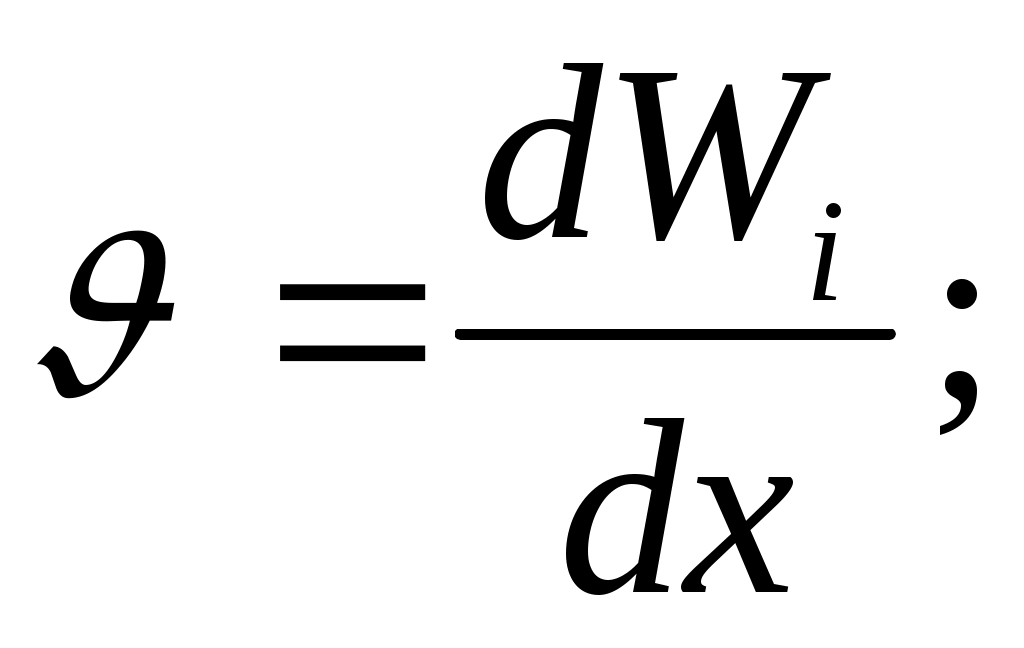
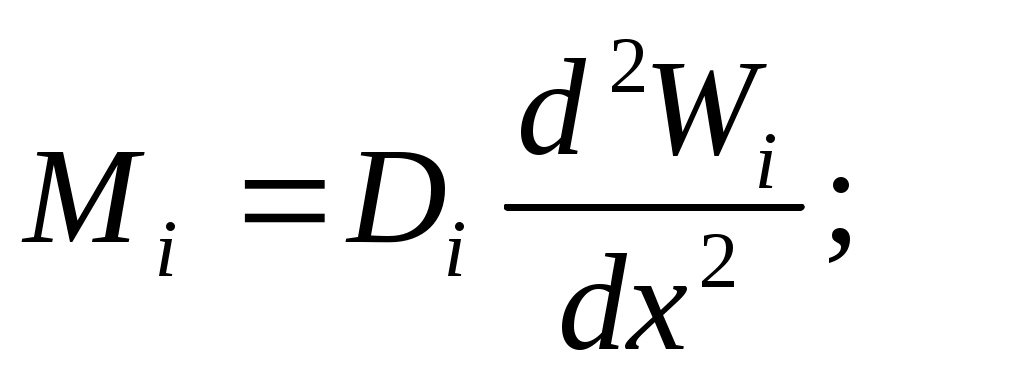
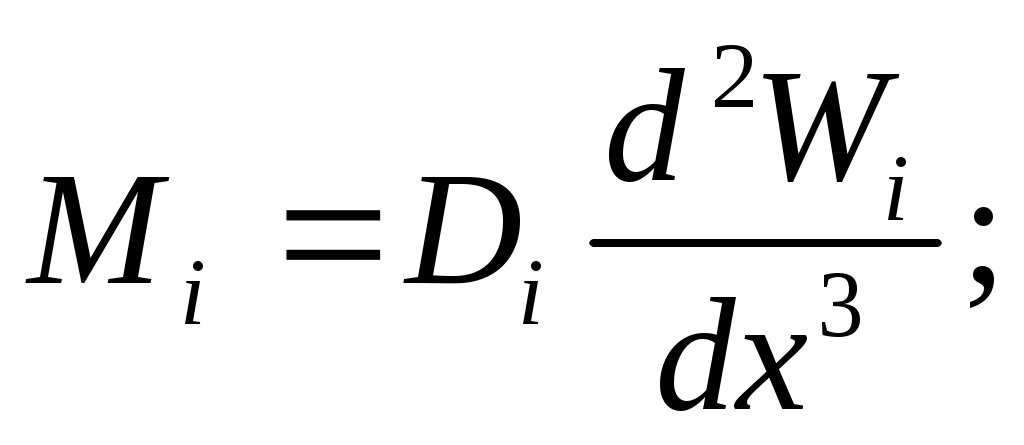
где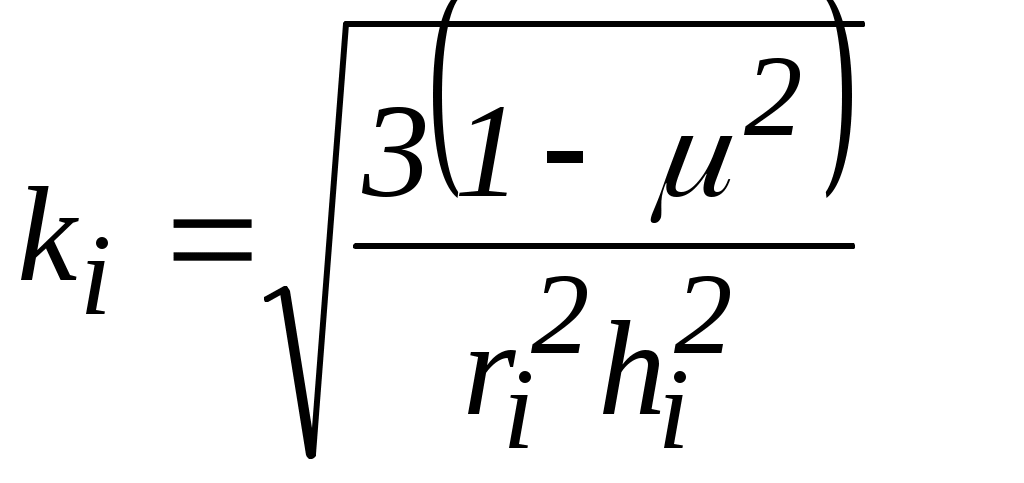 – параметр оболочки;
– параметр оболочки;
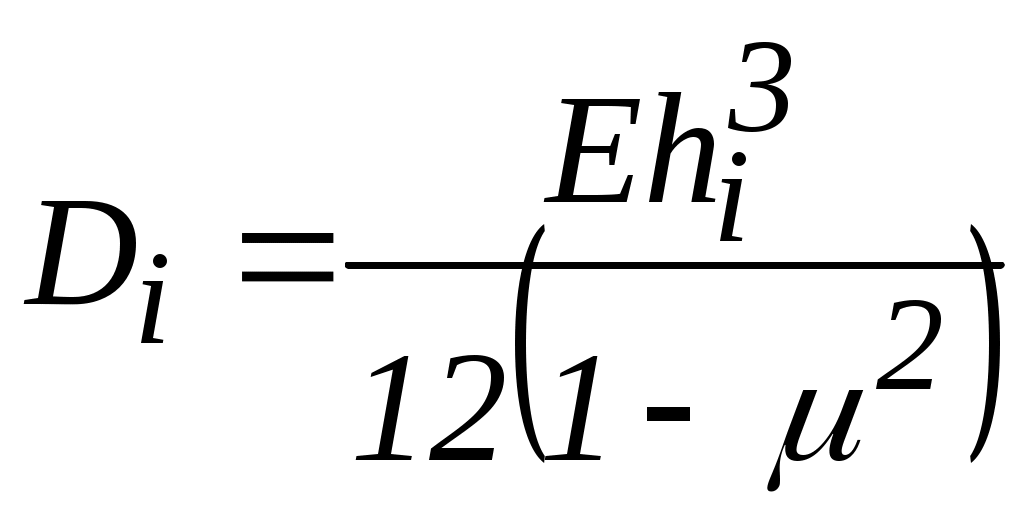 – жесткость i-го участка на изгиб
– жесткость i-го участка на изгиб 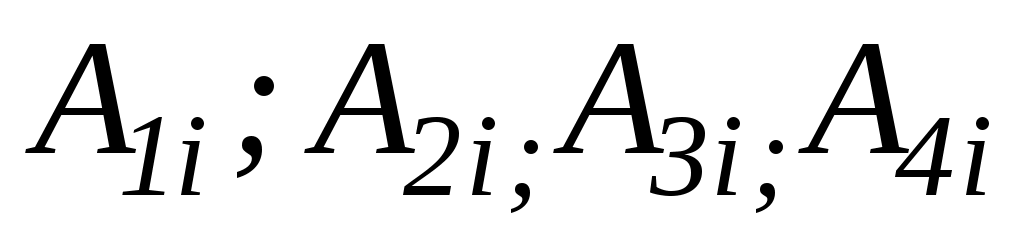 – постоянные, определяемые из граничных условий;
– постоянные, определяемые из граничных условий;
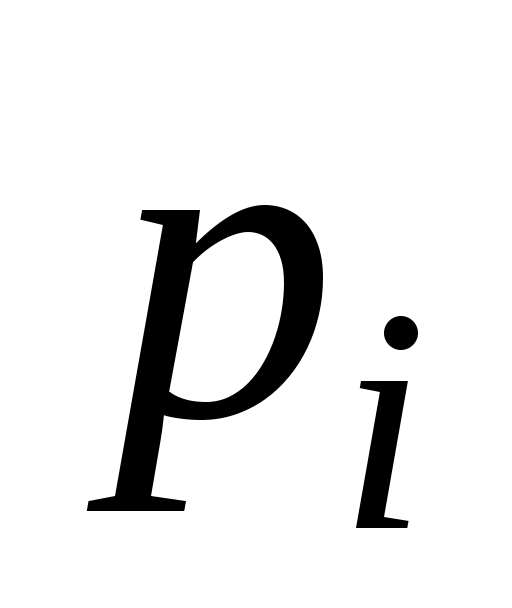 – внутреннее давление на i-м участке, приведенное к срединной поверхности;
– внутреннее давление на i-м участке, приведенное к срединной поверхности;
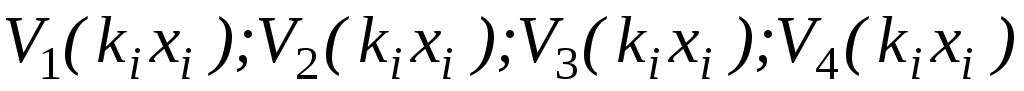 – функции Крылова;
– функции Крылова;
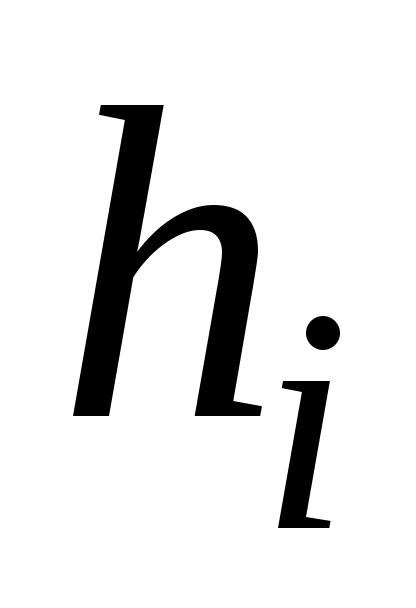 – толщина стенки гильзы на i-м участке;
– толщина стенки гильзы на i-м участке;
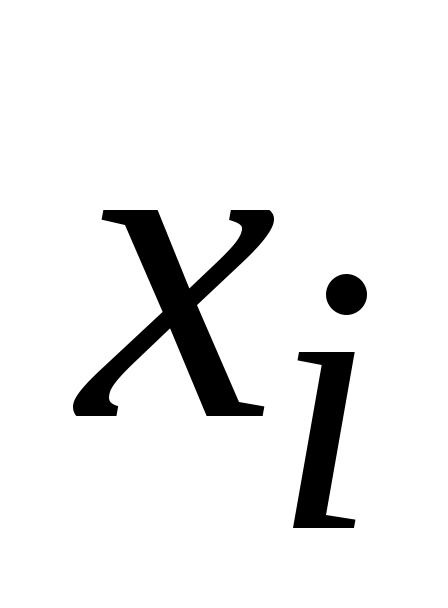 – координата участка по оси гильзы;
– координата участка по оси гильзы;
μ– коэффициент Пуассона;
E – модуль упругости.
Если длина участка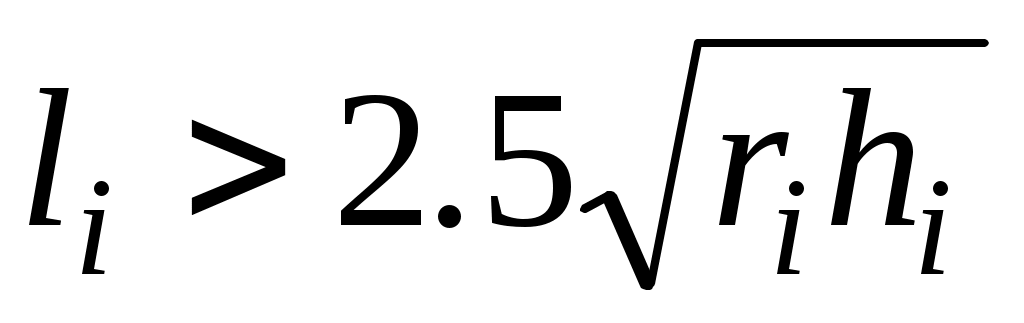 , то влиянием граничных условий на одном торце участка на распределение деформаций вблизи второго торца можно пренебречь. Для этого участка функции и нужно брать по формулам теории длинных цилиндрических оболочек. Так,
, то влиянием граничных условий на одном торце участка на распределение деформаций вблизи второго торца можно пренебречь. Для этого участка функции и нужно брать по формулам теории длинных цилиндрических оболочек. Так,
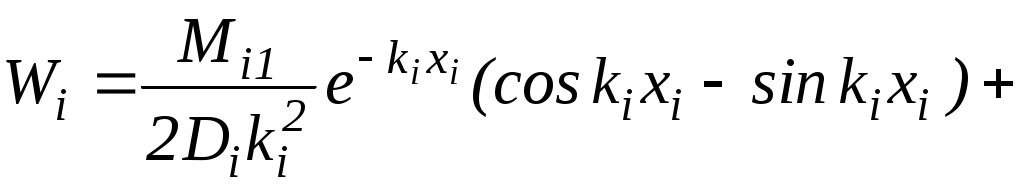
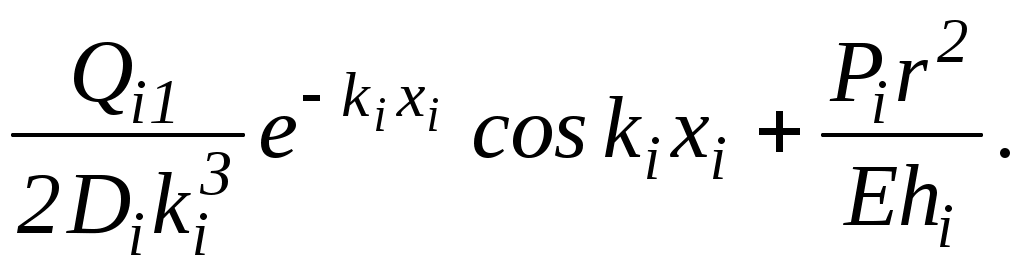
Можно, переходя последовательно от участка к участку, выразить постоянные интегрирования для всех участков гильзы через два неизвестных начальных параметра первого участка.
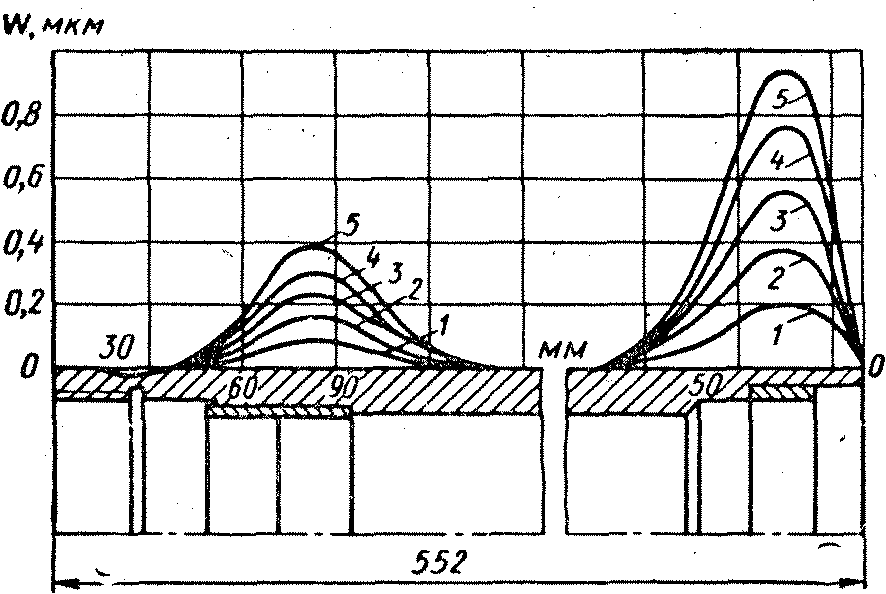
Рисунок 6 – Графики отклонения формы высокоточной гильзы,
установленной для шлифования на специальные зажимные устройства с гофрированными втулками:
1) Р=2кгс/см2; 2) Р=4кгс/см2; 3) Р=6кгс/см2;
4) Р=8кгс/см2; 5) Р=10кгс/см2.
Можно, переходя последовательно от участка к участку, выразить постоянные интегрирования для всех участков гильзы через два неизвестных начальных параметра первого участка.
На рисунке 6 показаны результаты расчета по определению погрешности формы гильзы координатно-расточного станка мод. 2А450. Допуск на погрешность формы наружной поверхности составляет 2мкм. В расчете принято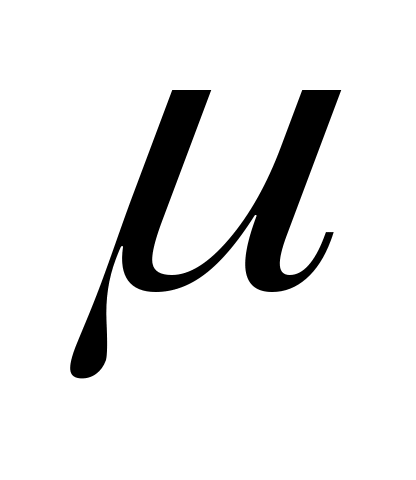 =0,3; E=2-10'кгс/см2. Графики показывают, что при давлении р = 10кгс/см2 отклонение формы у правого конца гильзы составит примерно 1,7 мкм, что близко к значению допустимого отклонения. Проведенные расчеты хорошо согласуются с экспериментальными данными.
=0,3; E=2-10'кгс/см2. Графики показывают, что при давлении р = 10кгс/см2 отклонение формы у правого конца гильзы составит примерно 1,7 мкм, что близко к значению допустимого отклонения. Проведенные расчеты хорошо согласуются с экспериментальными данными.
Существует также вполне четкая наследственная передача погрешностей торцовых установочных поверхностей деталей типа гильз на поверхность обрабатываемого отверстия. Из-за неплоскостности и непараллельности торцов зажимная сила не распределяется равномерно по торцовой поверхности, а действует лишь по некоторой ее части, составляющей сравнительно небольшую долю номинальной опорной поверхности. Наоборот, при закреплении высокоточных втулок или гильз по цилиндрической установочной поверхности может возникнуть неплоскостность обрабатываемых торцовых поверхностей. Расчет возникающей неплоскостности производят методом наложения с рассмотрением нескольких схем нагружения в соответствии с основной, расчетной схемой.
На рисунке 7,а представлена схема закрепления высокоточной гильзы на призме. Сила Р передается на гильзу через призматический прижим. При этом возникают не только радиальные упругие перемещения гильзы, но и искажения торца A. На рисунке 7,б даны результаты расчета и показана эпюра перемещений торцовой поверхности А после раскрепления гильзы, имеющей наружный диаметр 32, внутренний диаметр 28 и общую длину 127мм; сила закрепления 200кгс; неплоскостность превышает 4мкм. Аналогичные задачи могут быть решены с учетом влияния сил трения по линии контакта гильзы с призмой или иными зажимными элементами приспособления. Для того чтобы деформации в месте закрепления не передавались на обрабатываемый торец, расстояние l до этого торца должно удовлетворять следующему условию: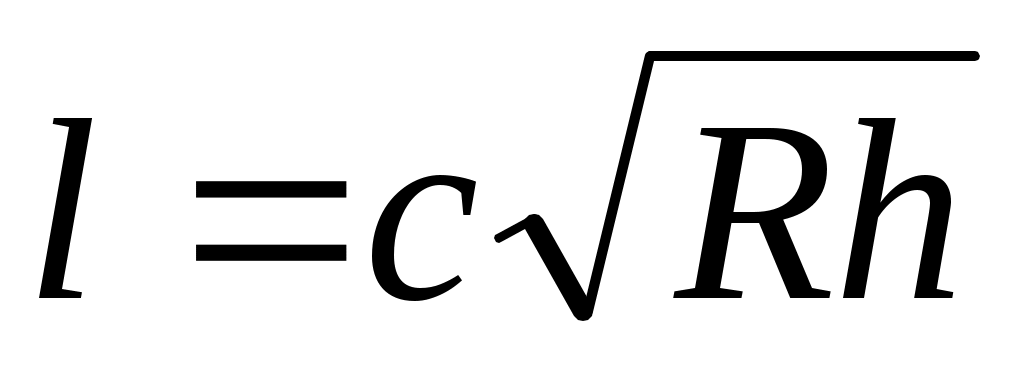 при k = 0;
при k = 0;
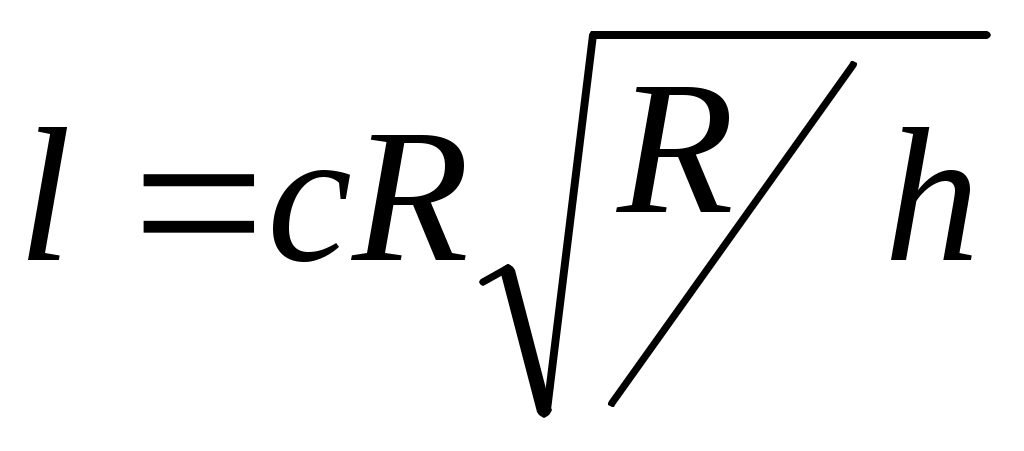
Аналогично для второго уравнения каждое из слагаемых представляет собой линейное перемещение сечения В в направлении силы N от заданной нагрузки Р (
где
приложенного в направлении неизвестного момента M,
Например,
а после некоторых преобразований
Если ε <0,1 (в большинстве случаев чистовой обработки имеем 0< ε <0,1), то ошибка, вызванная пренебрежением последнего члена, будет меньше 0,53%. Аналогичным методом находим EJxδ2P, EJxδ11, EJxδ22, EJxδ12, EJxδ21. Таким образом, канонические уравнения метода сил принимают вид
Решение уравнений дает
Если в последних формулах положить ε = 0, то получим известное решение M ≈ 0.1Pr; N = –0.577P. Для определения перемещений предварительно находят выражения изгибающих моментов
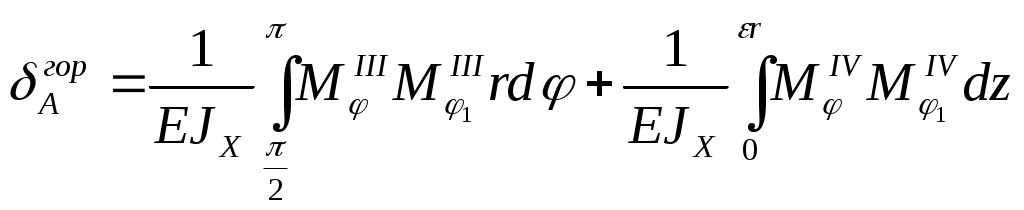
Для приведения уравнений, полученных с помощью данной методики, к виду, удобному для практического пользования, необходимо сделать ряд преобразований. Приведенные ранее значения М и N представим в виде
Значения коэффициентов k1– k11 следующие: k1= 23,66;
k2= 19,2816; k3= 130,8643; k4= 237,87; k5= 452,367; k6= 192,0; k7= =43,5296; k8= 83,136; k9=15,0; k10= 75,3978; k11= 96,0.
Аналогично, произведя преобразования, можно определять суммарное перемещение под тремя кулачками, закрепляющими некруглое кольцо:
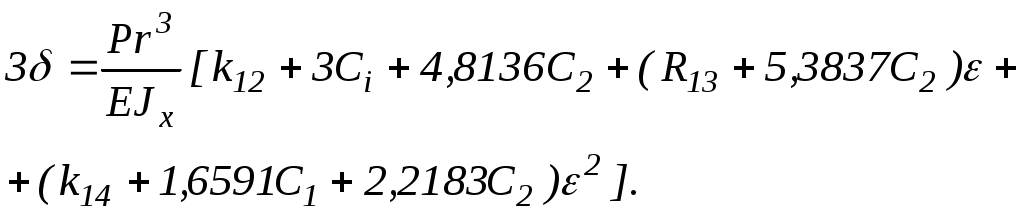
Здесь значения k12=2,5273; k13=2,50; k14=5,4877. Коэффициенты
= 0,082;
Зажимные устройства способны создавать отклонения формы на заготовках и деталях, которые до закрепления таких отклонений не имели. Поэтому можно считать, что в этих случаях зажимные устройства порождают погрешность формы. Допустим, что высокоточную гильзу закрепляют в двух местах с базированием по отверстию двумя гофрированными втулками (см. рисунок 2,г) для проведения шлифования. Зажимное приспособление создает осесимметричное нагружение; нагрузка распределенная. При снятии сил закрепления после обработки деформация гильзы исчезает. Это приводит к искажению формы обработанной поверхности. В связи с этим возникает необходимость оценки величины деформации, вызванной силами закрепления.
Возможно решение обратной задачи: определение такой силы закрепления, которая вызывала бы допустимую деформацию. Искажения формы закрепляемых гильз могут быть определены на основе теории осесимметричной деформации цилиндрических оболочек. В общем случае высокоточная гильза может быть представлена состоящей из отдельных участков в зависимости от геометрических параметров и характера нагружения. Действие одного участка на другой заменяется изгибающим моментом М и поперечной силой Q. Обозначим все величины, относящиеся к началу i-го участка, индексом: 1, а к концу – индексом i2. Радиусы срединной поверхности i-го и i+1-го участков могут быть различными и равными соответственно r1 и ri+1 Силовые факторы в конце предыдущего и в начале следующего участков связаны между собой следующими зависимостями:
Для коротких участков гильзы выражения для радиального перемещения W, угла
где
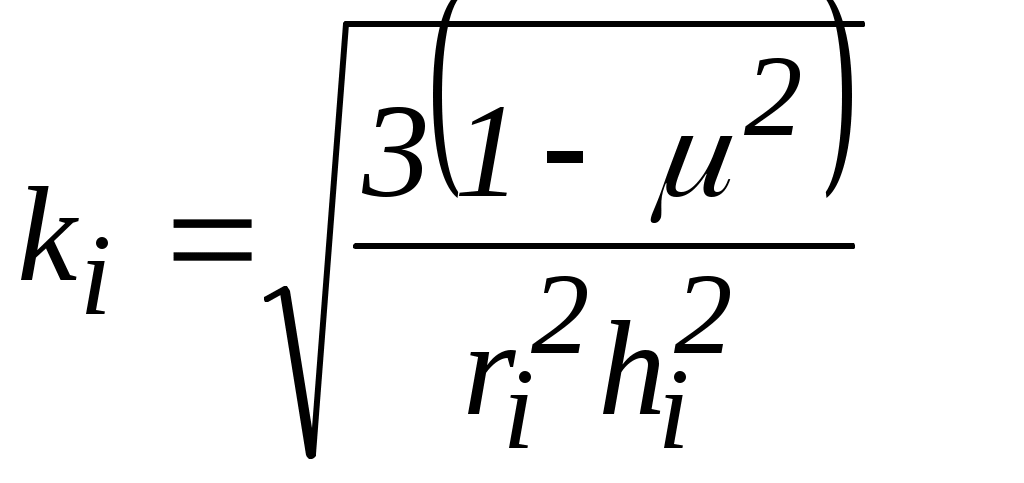 – параметр оболочки;
– параметр оболочки; μ– коэффициент Пуассона;
E – модуль упругости.
Если длина участка
Можно, переходя последовательно от участка к участку, выразить постоянные интегрирования для всех участков гильзы через два неизвестных начальных параметра первого участка.

Рисунок 6 – Графики отклонения формы высокоточной гильзы,
установленной для шлифования на специальные зажимные устройства с гофрированными втулками:
1) Р=2кгс/см2; 2) Р=4кгс/см2; 3) Р=6кгс/см2;
4) Р=8кгс/см2; 5) Р=10кгс/см2.
Можно, переходя последовательно от участка к участку, выразить постоянные интегрирования для всех участков гильзы через два неизвестных начальных параметра первого участка.
На рисунке 6 показаны результаты расчета по определению погрешности формы гильзы координатно-расточного станка мод. 2А450. Допуск на погрешность формы наружной поверхности составляет 2мкм. В расчете принято
Существует также вполне четкая наследственная передача погрешностей торцовых установочных поверхностей деталей типа гильз на поверхность обрабатываемого отверстия. Из-за неплоскостности и непараллельности торцов зажимная сила не распределяется равномерно по торцовой поверхности, а действует лишь по некоторой ее части, составляющей сравнительно небольшую долю номинальной опорной поверхности. Наоборот, при закреплении высокоточных втулок или гильз по цилиндрической установочной поверхности может возникнуть неплоскостность обрабатываемых торцовых поверхностей. Расчет возникающей неплоскостности производят методом наложения с рассмотрением нескольких схем нагружения в соответствии с основной, расчетной схемой.
На рисунке 7,а представлена схема закрепления высокоточной гильзы на призме. Сила Р передается на гильзу через призматический прижим. При этом возникают не только радиальные упругие перемещения гильзы, но и искажения торца A. На рисунке 7,б даны результаты расчета и показана эпюра перемещений торцовой поверхности А после раскрепления гильзы, имеющей наружный диаметр 32, внутренний диаметр 28 и общую длину 127мм; сила закрепления 200кгс; неплоскостность превышает 4мкм. Аналогичные задачи могут быть решены с учетом влияния сил трения по линии контакта гильзы с призмой или иными зажимными элементами приспособления. Для того чтобы деформации в месте закрепления не передавались на обрабатываемый торец, расстояние l до этого торца должно удовлетворять следующему условию: