Файл: Методические указания к выполнению контрольной работы 3 для студентов зф и идо.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 206
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, а  = (310) эВ, поэтому тепловому возбуждению подвергается лишь незначительная доля (менее 1 ) общего числа электронов в валентной зоне металла, энергия которых отличается от
= (310) эВ, поэтому тепловому возбуждению подвергается лишь незначительная доля (менее 1 ) общего числа электронов в валентной зоне металла, энергия которых отличается от  не более чем на величину
не более чем на величину  (рис. 5.4,б). Функция распределения при этом размывается, но незначительно. Следовательно, концентрация свободных электронов в металле практически не зависит от температуры и с хорошей точностью определяется выражением (5.3).
(рис. 5.4,б). Функция распределения при этом размывается, но незначительно. Следовательно, концентрация свободных электронов в металле практически не зависит от температуры и с хорошей точностью определяется выражением (5.3).
Заметим, что вероятность заполнения уровня при
при 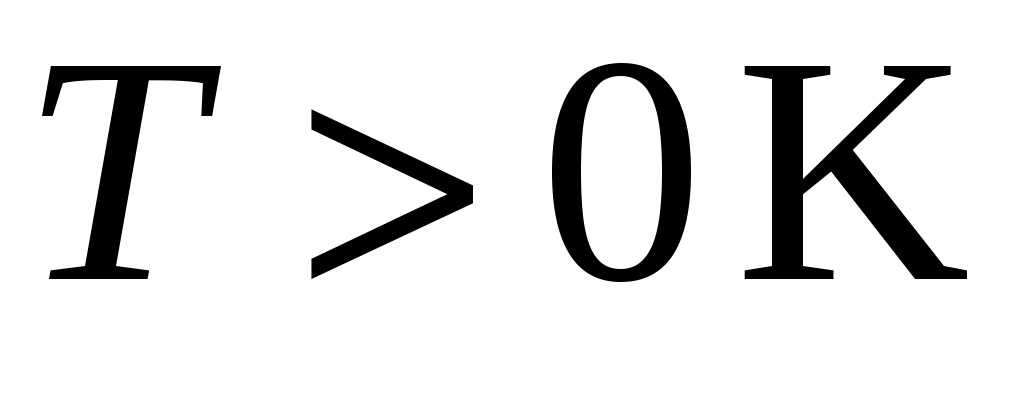 равна
равна 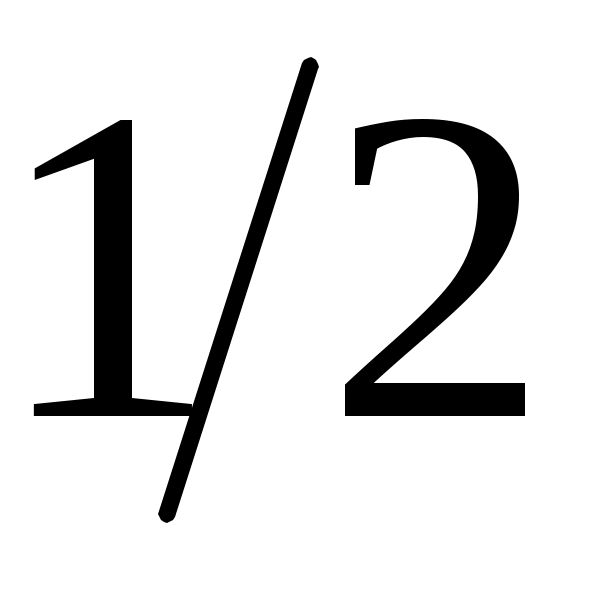 .
.
Задача. Концентрация свободных электронов в металле равна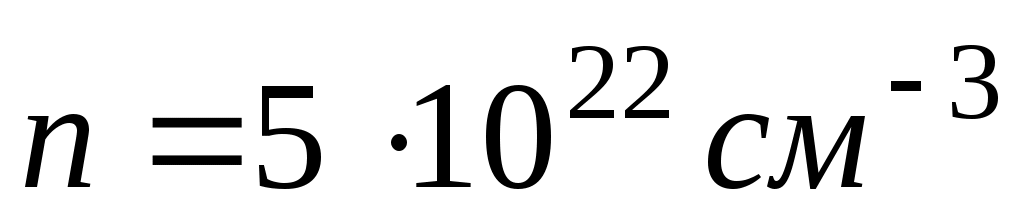 . Найдите среднее значение энергии свободных электронов при абсолютном нуле.
. Найдите среднее значение энергии свободных электронов при абсолютном нуле.
Дано: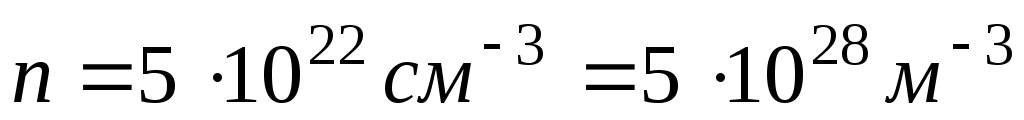

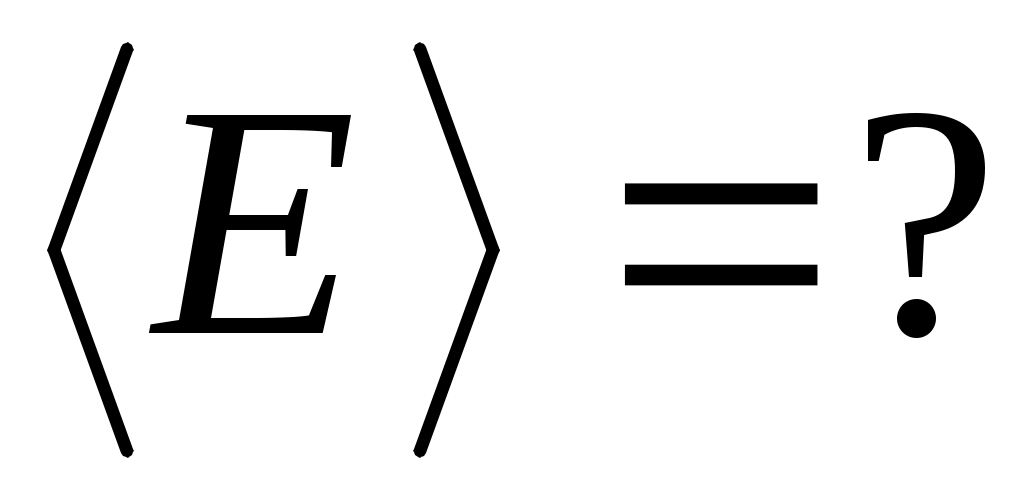
Решение. Среднюю энергию найдем как отношение полной энергии свободных электронов в единице объема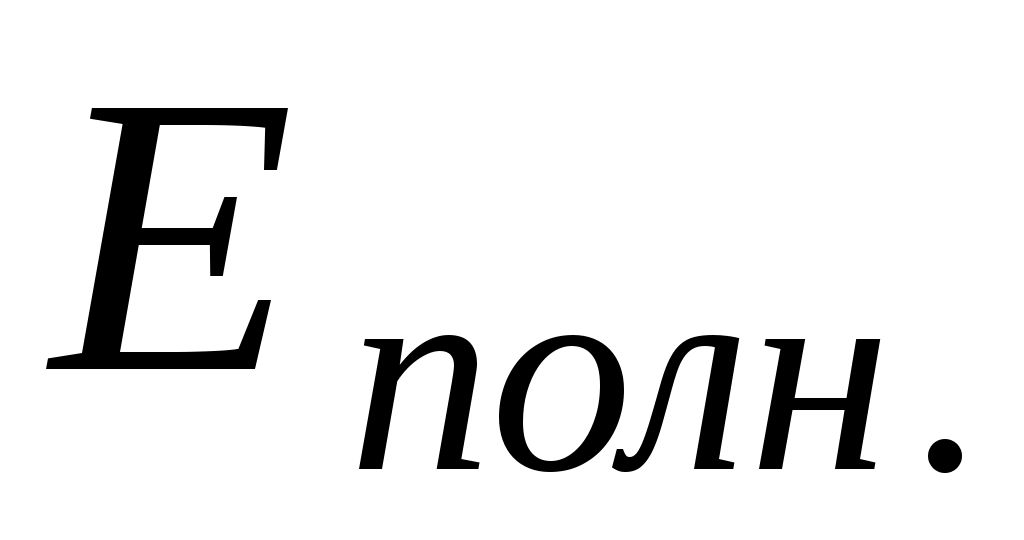 к концентрации свободных электронов
к концентрации свободных электронов 
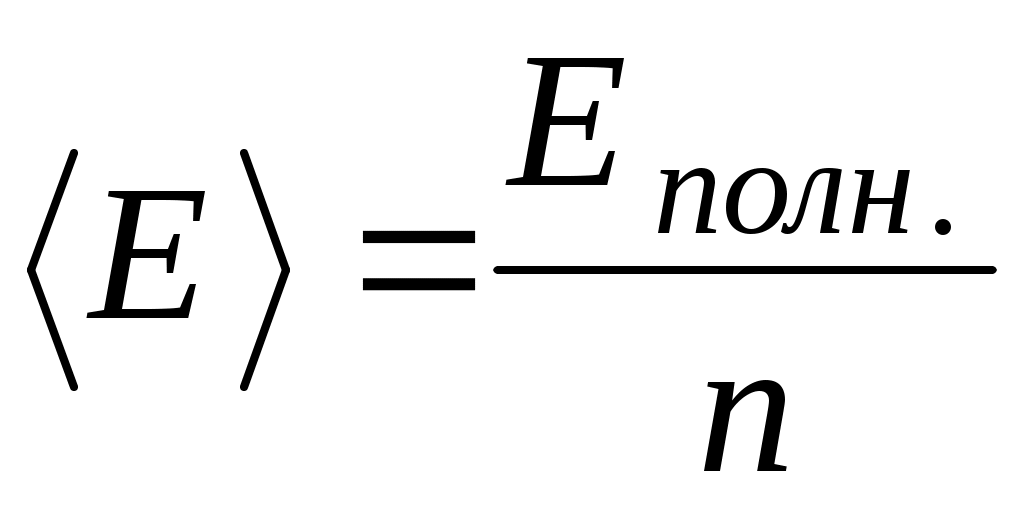 . (5.7)
. (5.7)
При все энергетические уровни вплоть до
все энергетические уровни вплоть до  заняты электронами. С учетом выражений (5.1), (5.2), (5.4) найдем
заняты электронами. С учетом выражений (5.1), (5.2), (5.4) найдем 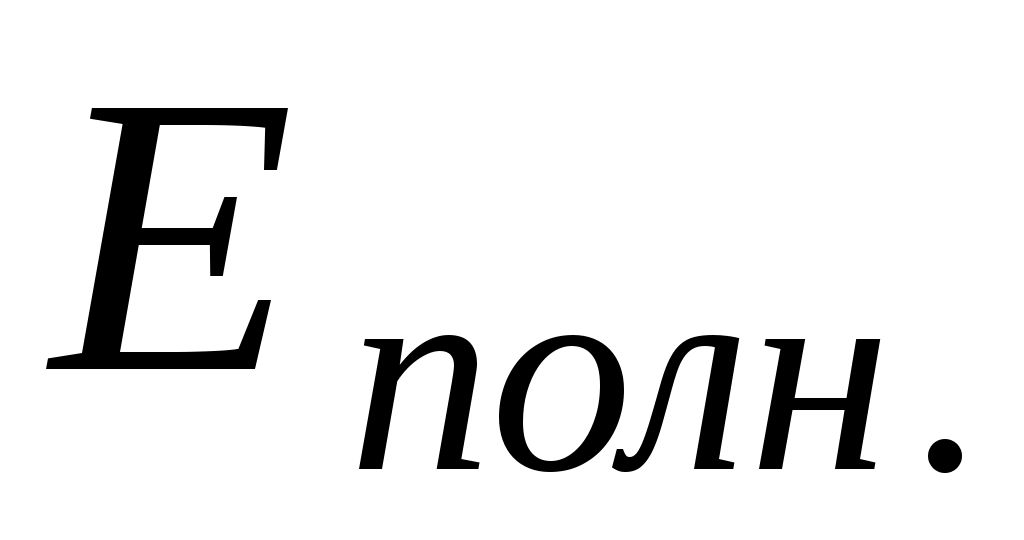
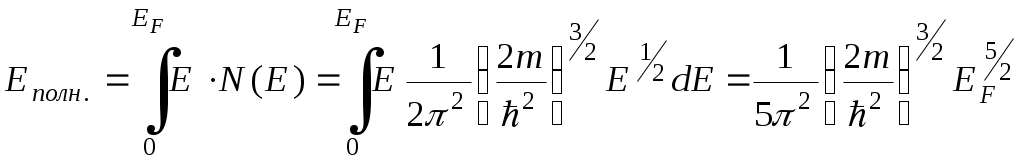 . (5.8)
. (5.8)
Подставляя (5.8) в (5.7) и учитывая формулы (5.5), (5.6), находим
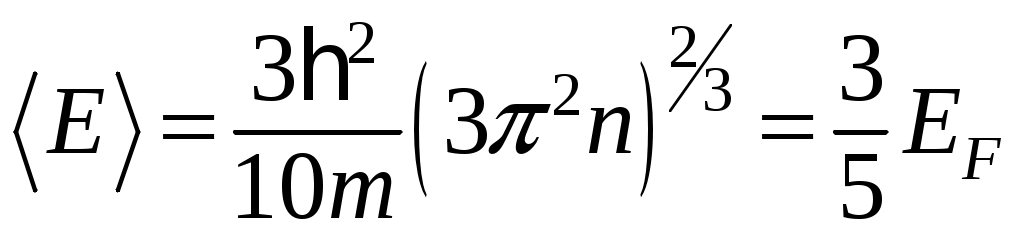
.
Проверяем единицу измерения
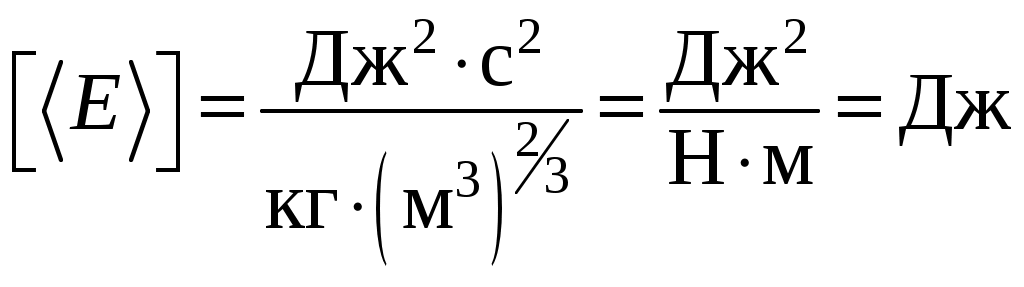 .
.
Вычислим
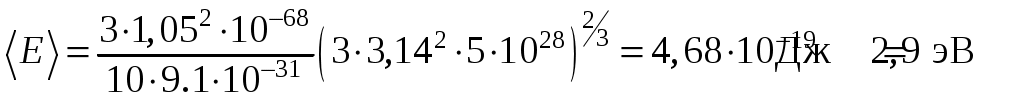 .
.
Результат показывает, что с точки зрения квантовой теории электронный газ в металле при абсолютном нуле имеет энергию, которая соответствует температуре, в ее классическом понимании по порядку величины равной,
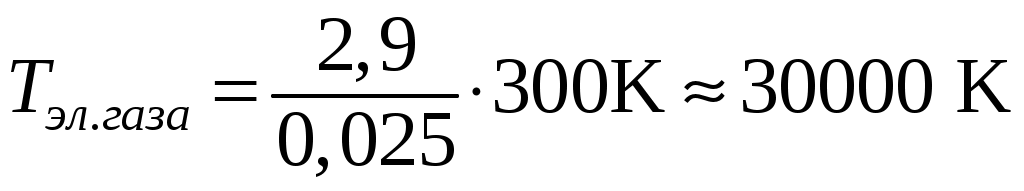 .
.
4. Рассмотрим элементы теории электропроводности собственных и примесных полупроводников.
Выше говорилось, что полупроводники при температуре являются диэлектриками. Они имеют небольшую ширину запрещенной зоны, поэтому уже при температурах, близких к комнатной, вследствие теплового возбуждения происходит переход части электронов с «потолка» валентной зоны на «дно» зоны проводимости. При этом проводимость полупроводника обусловливается как этими электронами (электронная составляющая проводимости), так и появившимися в валентной зоне вакансиями – «дырками» (дырочная составляющая проводимости). Электроны, перешедшие в валентную зону и дырки, расположенные в валентной зоне, могут перемещаться под действием приложенного к полупроводнику внешнего электрического поля, то есть являются свободными носителями заряда. Процесс образования (генерации) электронно-дырочных пар при постоянной температуре полупроводника уравновешен обратным процессом рекомбинации свободных электронов и дырок. Описанный процесс, при котором концентрации электронов проводимости и дырок одинаковы
являются диэлектриками. Они имеют небольшую ширину запрещенной зоны, поэтому уже при температурах, близких к комнатной, вследствие теплового возбуждения происходит переход части электронов с «потолка» валентной зоны на «дно» зоны проводимости. При этом проводимость полупроводника обусловливается как этими электронами (электронная составляющая проводимости), так и появившимися в валентной зоне вакансиями – «дырками» (дырочная составляющая проводимости). Электроны, перешедшие в валентную зону и дырки, расположенные в валентной зоне, могут перемещаться под действием приложенного к полупроводнику внешнего электрического поля, то есть являются свободными носителями заряда. Процесс образования (генерации) электронно-дырочных пар при постоянной температуре полупроводника уравновешен обратным процессом рекомбинации свободных электронов и дырок. Описанный процесс, при котором концентрации электронов проводимости и дырок одинаковы 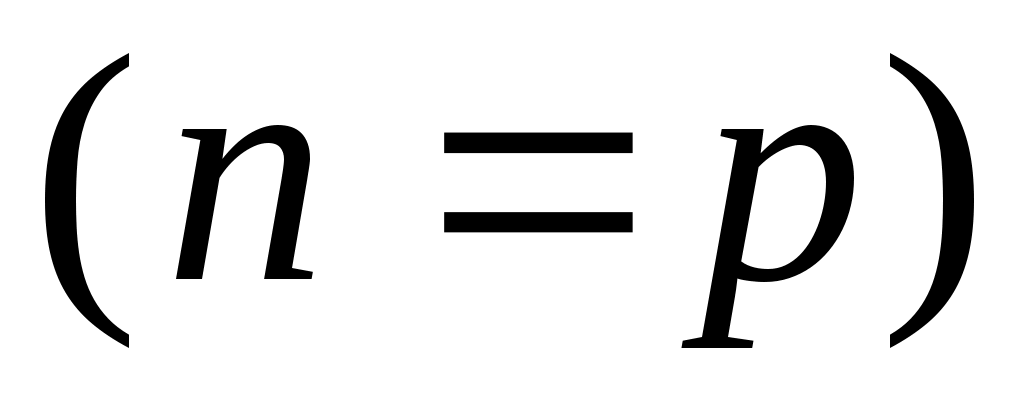 , характерен для собственных полупроводников. Удельная электропроводность
, характерен для собственных полупроводников. Удельная электропроводность  (величина, обратная удельному сопротивлению вещества
(величина, обратная удельному сопротивлению вещества 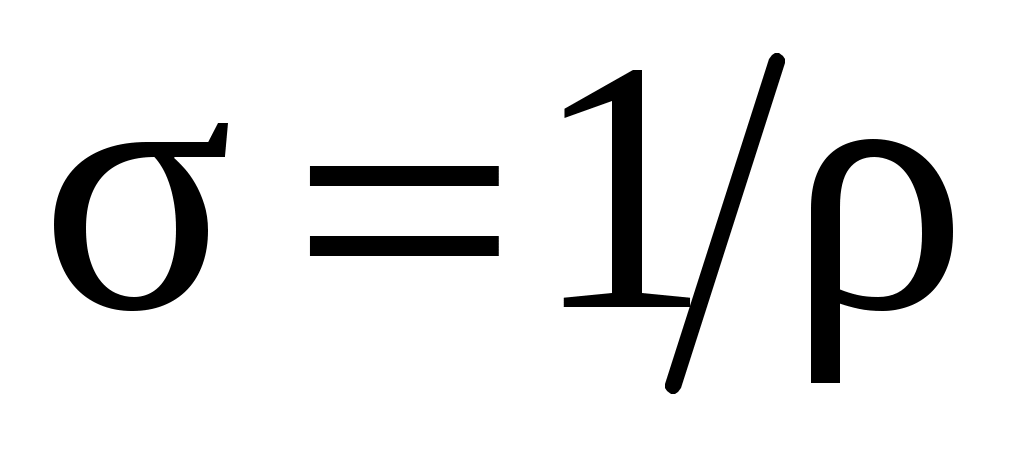 ) для этих полупроводников определяется выражением
) для этих полупроводников определяется выражением
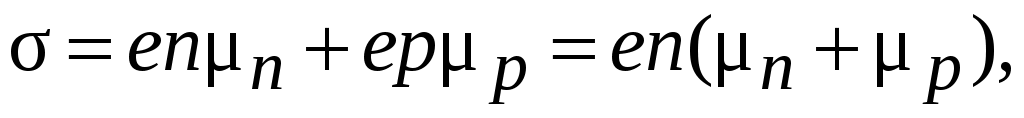 (5.9)
(5.9)
где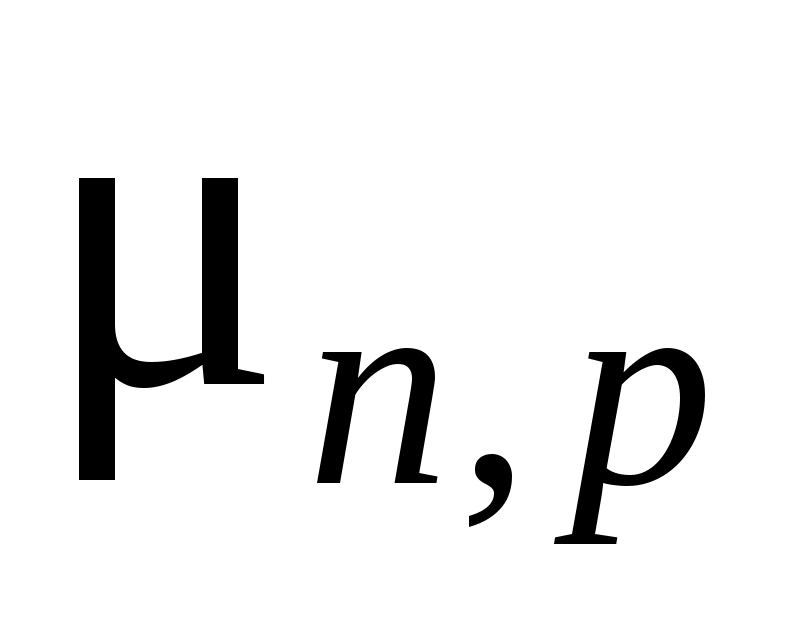
– подвижность электронов и дырок, которая характеризует среднюю дрейфовую скорость носителей тока под действием электрического поля единичной напряженности (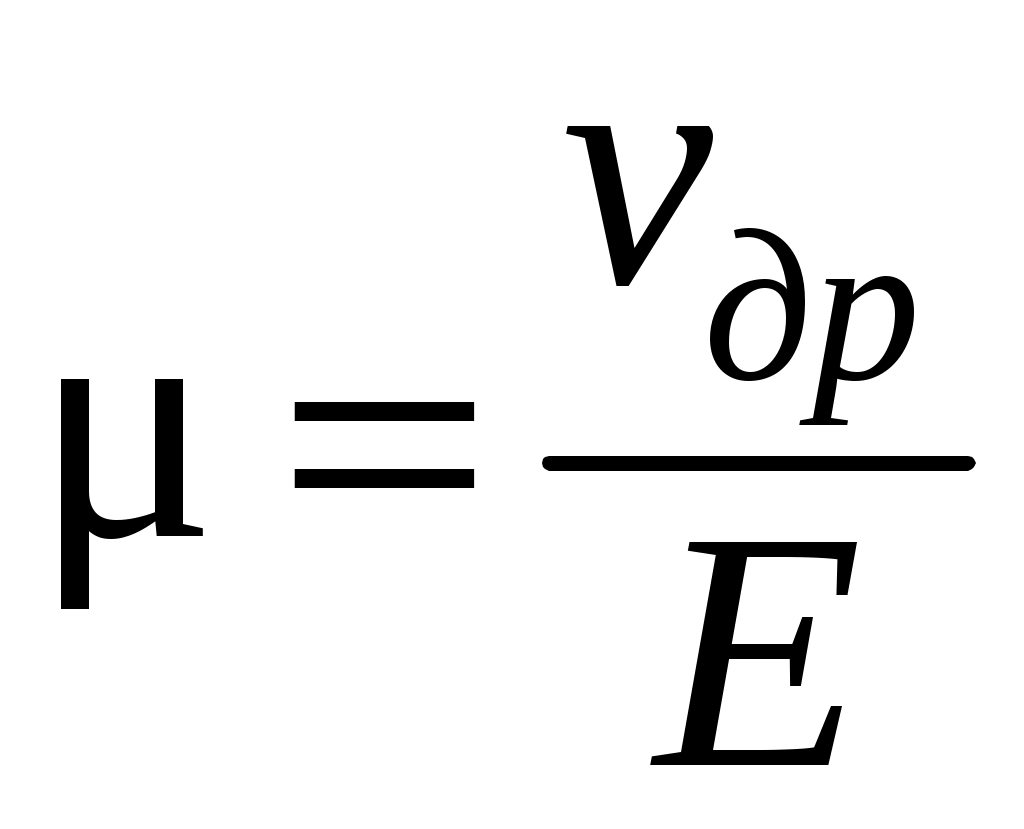 ).
).
Уровень энергии Ферми в собственных полупроводниках расположен вблизи середины запрещенной зоны (рис. 5.4,а).

Рис. 5.4. Расположение уровня энергии Ферми и примесных уровней
в полупроводниках при температуре Т = 0 К:
а – собственный; б – донорный; в - акцепторный
Электропроводность собственных полупроводников увеличивается с ростом температуры и зависит от ширины запрещенной зоны
и зависит от ширины запрещенной зоны 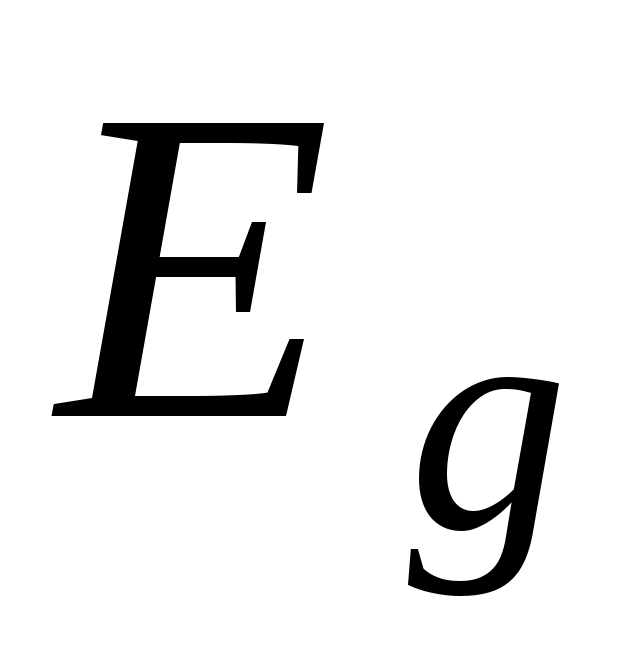 :
:
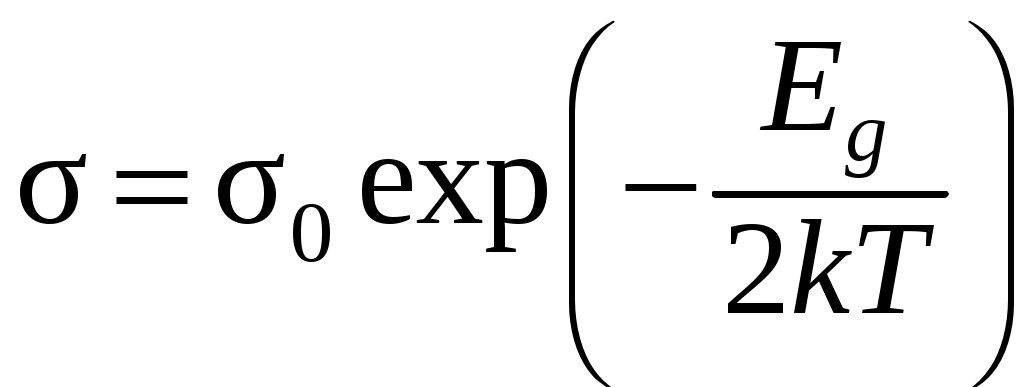 , (5.10)
, (5.10)
где – постоянная Больцмана.
– постоянная Больцмана.
Электропроводность примесных полупроводников обусловлена наличием в них примесных атомов, валентность которых больше (донорная примесь), или меньше (акцепторная примесь), чем у собственных атомов. Введение в собственный полупроводник примеси приводит к появлению в запрещенной зоне собственного полупроводника примесных уровней энергии. Для донорных полупроводников примесный уровень расположен вблизи дна зоны проводимости, а для акцепторных – вблизи потолка валентной зоны (рис. 5.4, б, в). Поскольку энергия активации примесей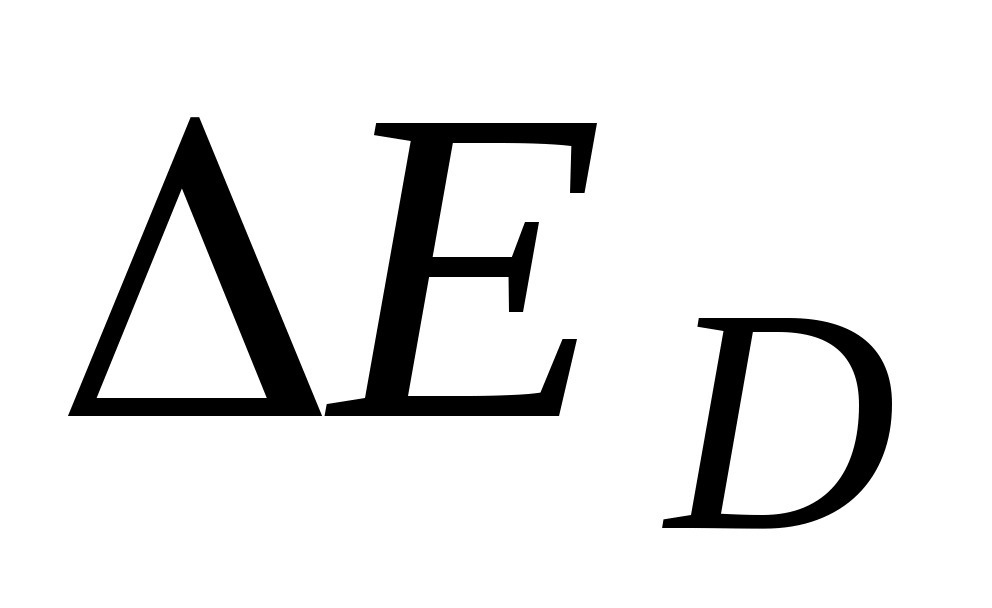 и
и 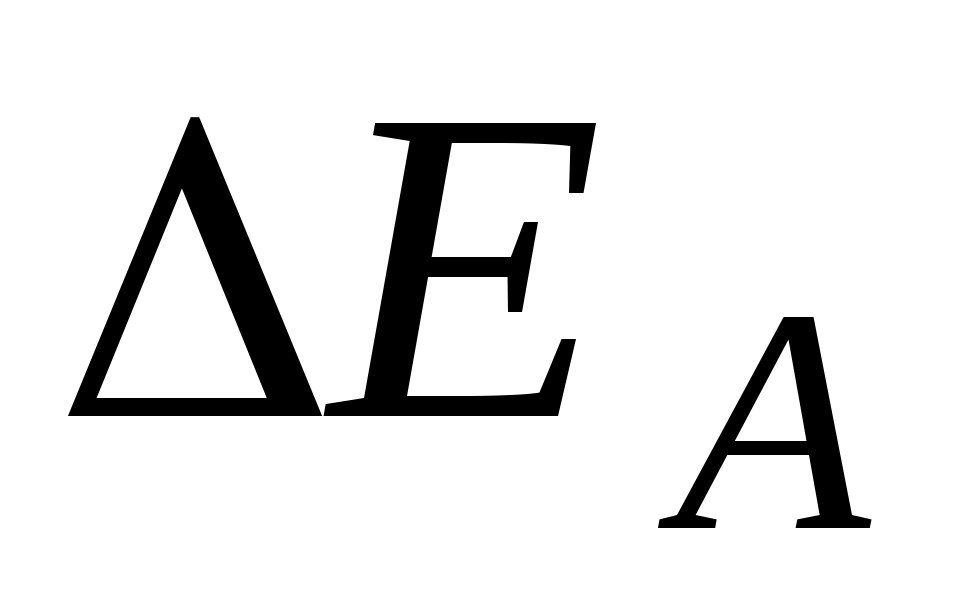 много меньше ширины запрещенной зоны, то уже при низких температурах (десятки кельвинов) в примесных полупроводниках появляются носители тока: электроны – в донорных, дырки – в акцепторных. При этом удельная электропроводность для полупроводников n – типа (донорного) и p – типа (акцепторного) определяется соответственно
много меньше ширины запрещенной зоны, то уже при низких температурах (десятки кельвинов) в примесных полупроводниках появляются носители тока: электроны – в донорных, дырки – в акцепторных. При этом удельная электропроводность для полупроводников n – типа (донорного) и p – типа (акцепторного) определяется соответственно
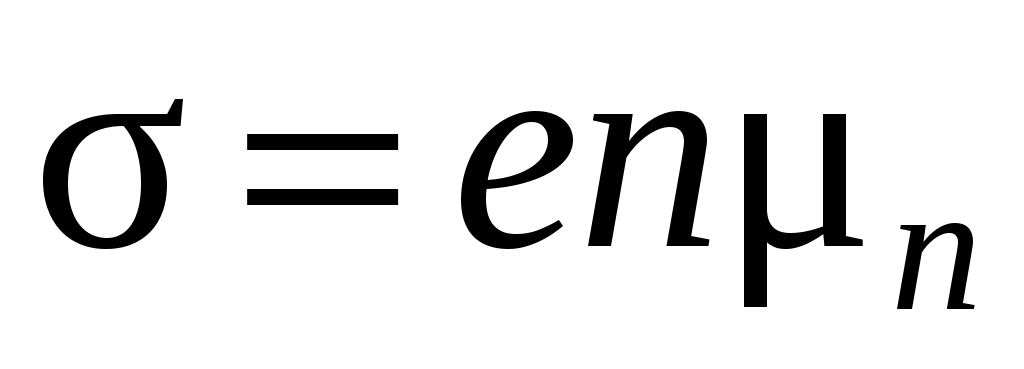 и
и 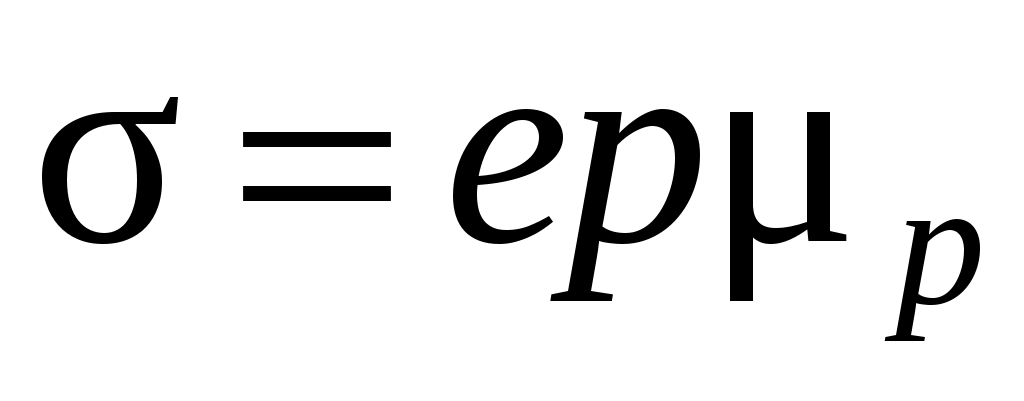 .
.
Тип носителей тока и их концентрацию можно определить экспериментально с помощью эффекта Холла по знаку и величине постоянной Холла
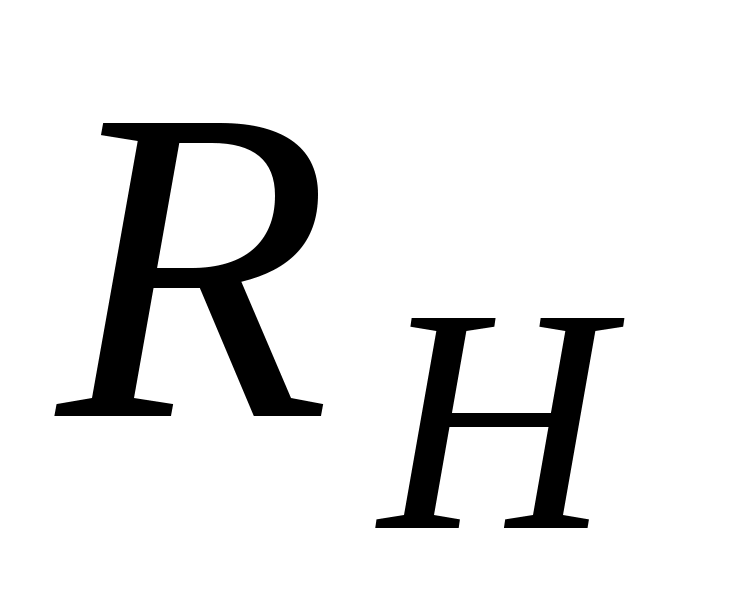 .
.
Для полупроводника n-типа, у которого основными носителями тока являются электроны,
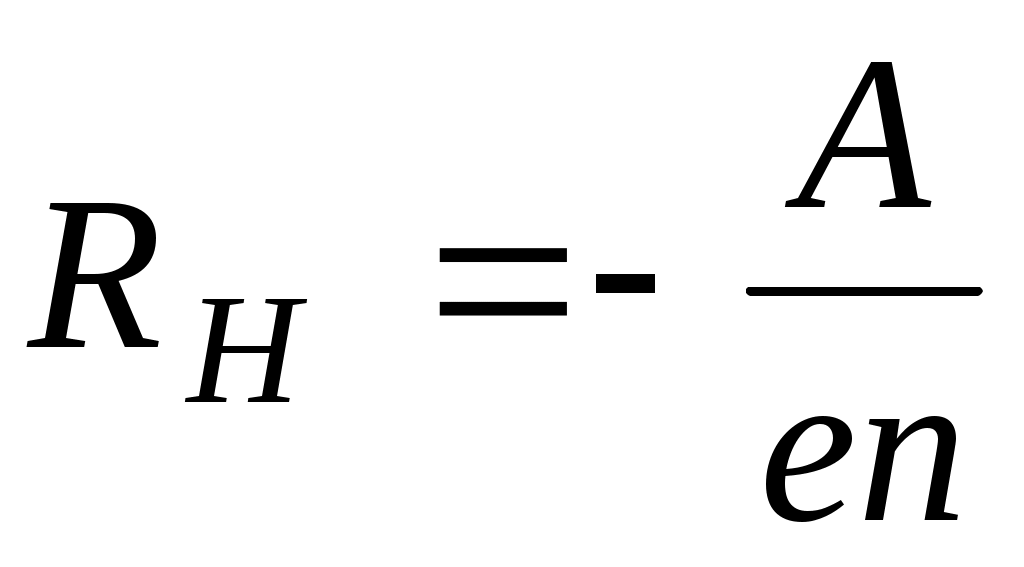 ;
;
для полупроводника р – типа, у которого основными носителями тока являются дырки,
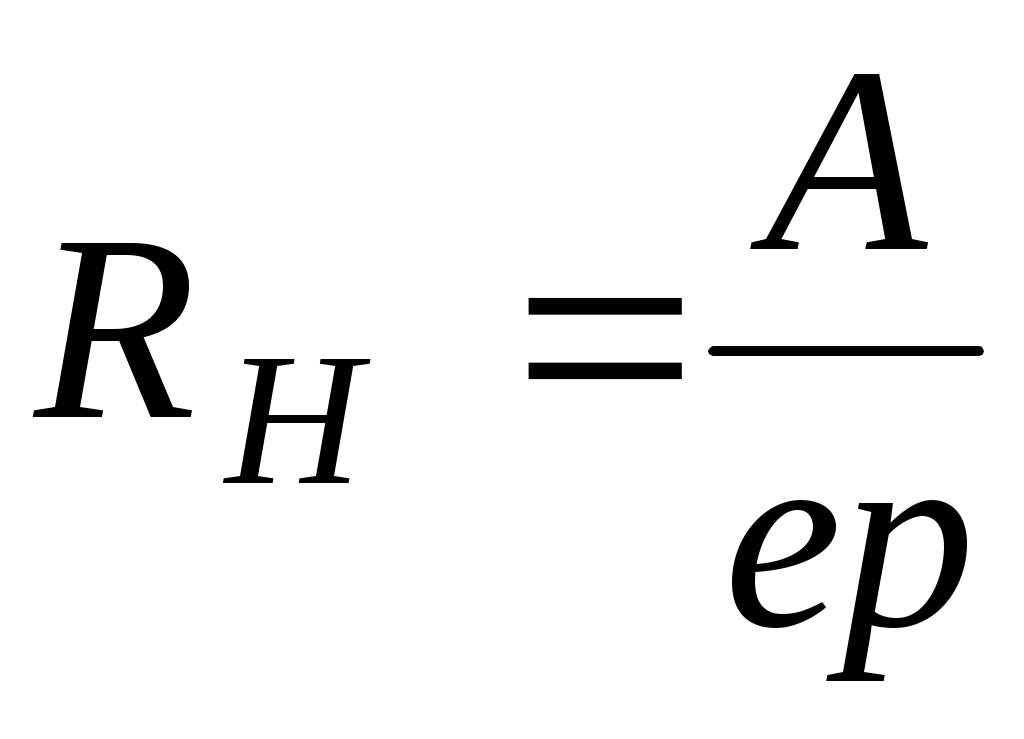 ;
;
для собственного (n = p)
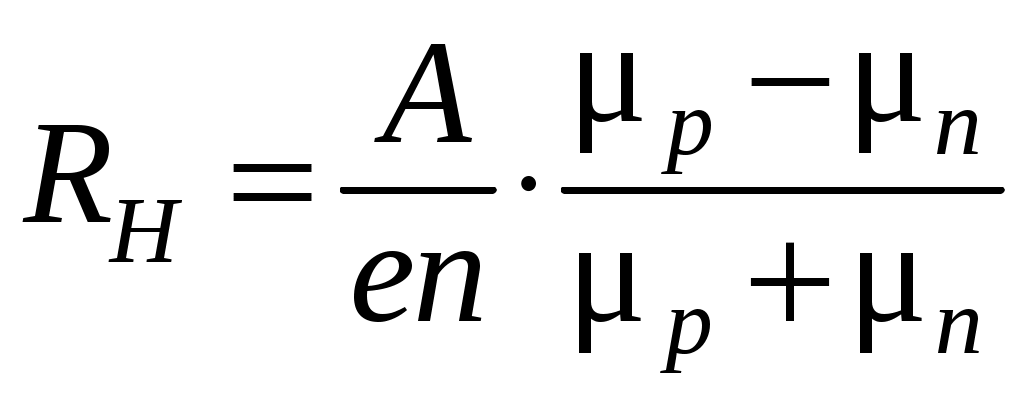 ,
,
где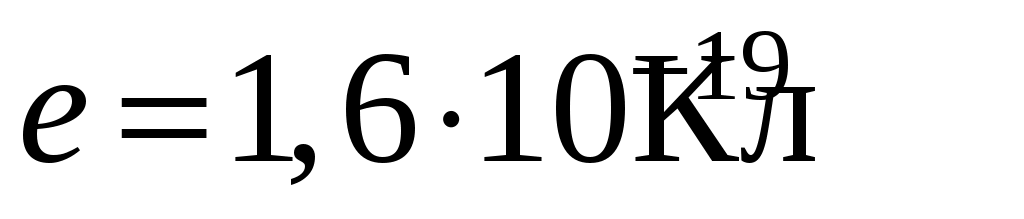 ; n, p – концентрация электронов и дырок соответственно;
; n, p – концентрация электронов и дырок соответственно;  – коэффициент, зависящий от механизма рассеяния носителей тока. В случае рассеяния носителей тока на тепловых колебаниях кристаллической решетки полупроводника, что обычно наблюдается при температурах близких и выше комнатной,
– коэффициент, зависящий от механизма рассеяния носителей тока. В случае рассеяния носителей тока на тепловых колебаниях кристаллической решетки полупроводника, что обычно наблюдается при температурах близких и выше комнатной, 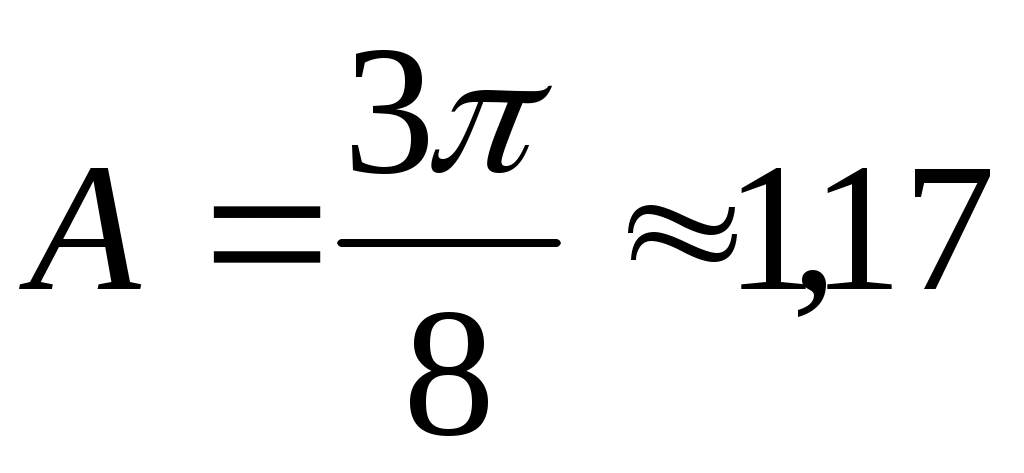 . Для металлов и вырожденных полупроводников
. Для металлов и вырожденных полупроводников  =1.
=1.
Дополнительные носители тока в полупроводниках могут возникать за счет поглощения света (фотонов). При этом, кроме удельной электропроводности, обусловленной тепловым возбуждением, появляется проводимость, обусловленная внутренним фотоэффектом,
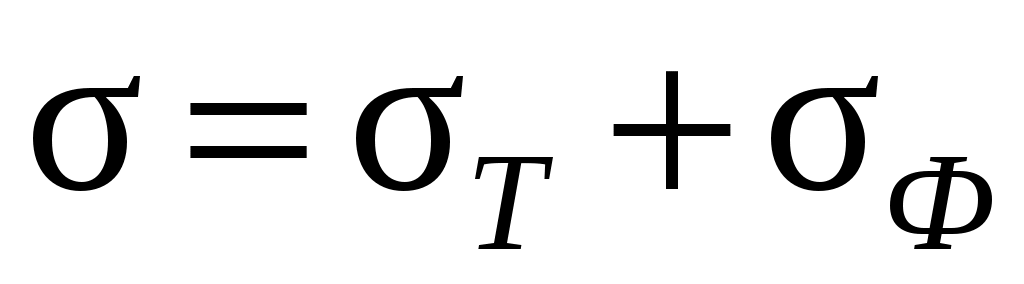 .
.
В случае собственного полупроводника фотопроводимость
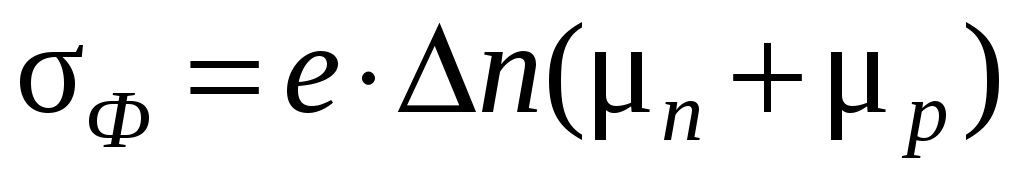 ,
,
где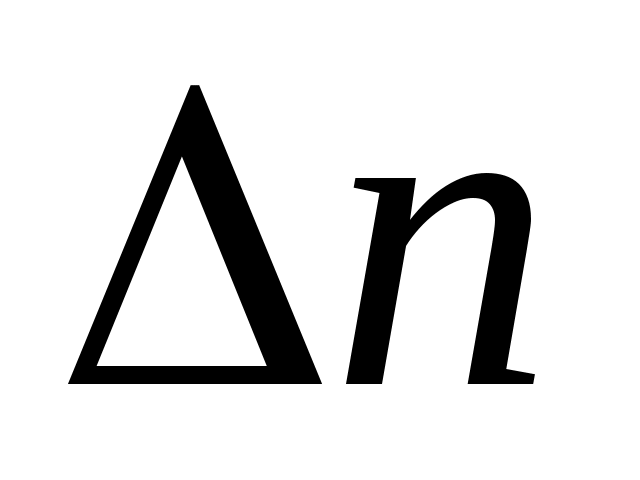 – число пар электрон – дырка, возникших при поглощении квантов
– число пар электрон – дырка, возникших при поглощении квантов
света.
Задача. Во сколько раз возрастет электропроводность образца кремния при нагревании его от температуры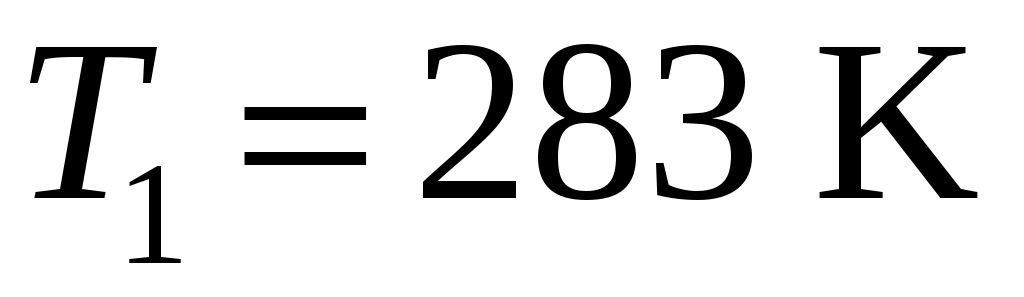 до температуры
до температуры 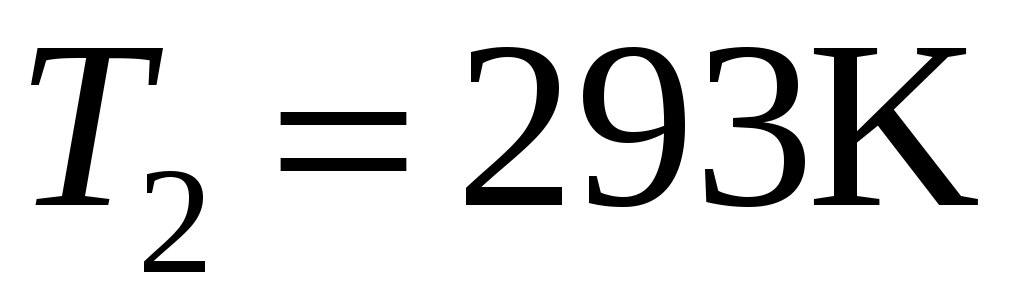 ? Ширина запрещенной зоны для кремния
? Ширина запрещенной зоны для кремния 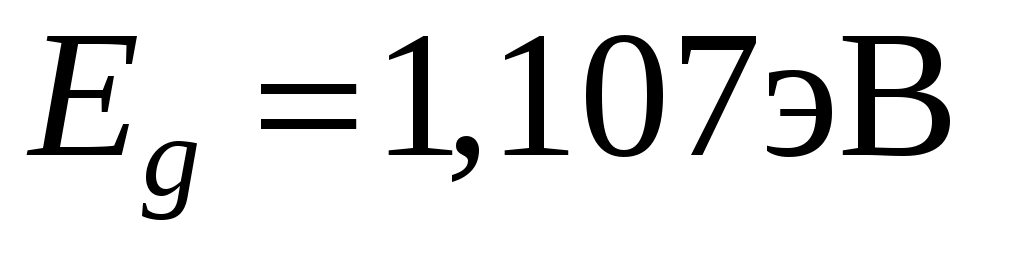 .
.
Дано: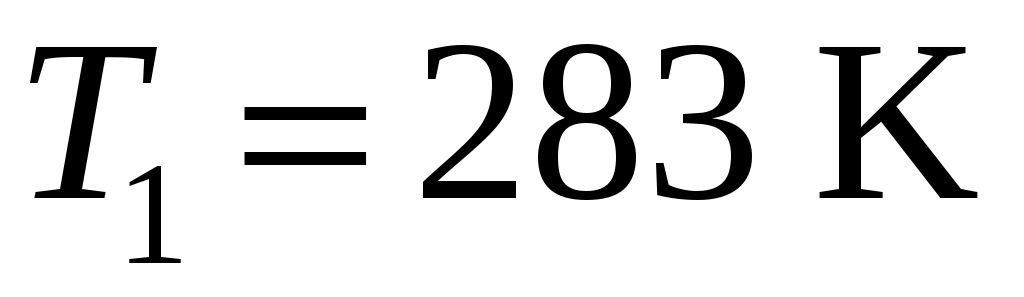 ,
,
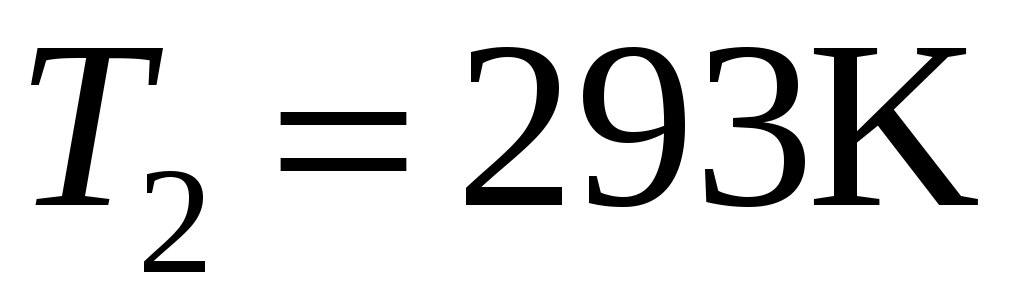 ,
,
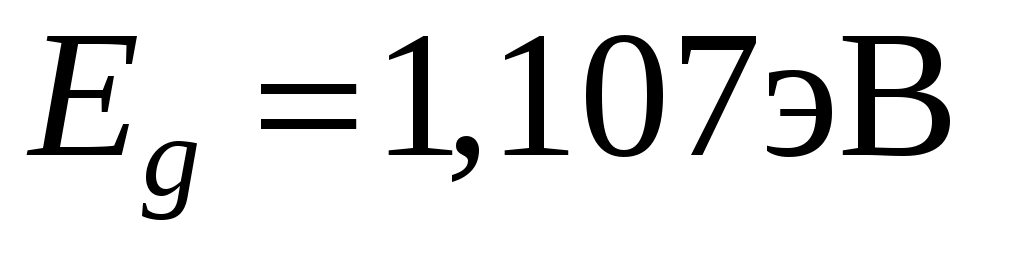
 – ?
– ?
Решение. Зависимость электропроводности собственных полупроводников от температуры
собственных полупроводников от температуры  определяется формулой
определяется формулой
 .
.
Вычисляя с помощью этой формулы отношение электропроводностей при заданных температурах, получаем

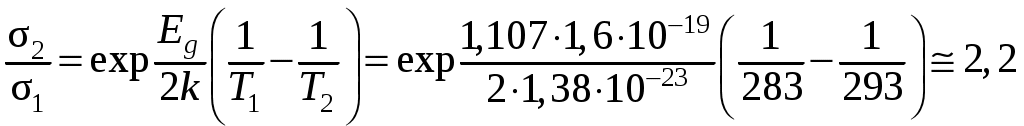 .
.
Ответ. Электропроводность увеличится в 2,2 раза.
Тема 7.
ЯДЕРНЫЕ РЕАКЦИИ. РАДИОАКТИВНОСТЬ
Радиоактивностью называют самопроизвольное превращение одних атомных ядер в другие, сопровождаемое испусканием элементарных частиц.
Отдельные радиоактивные ядра претерпевают превращение независимо друг от друга. Поэтому можно считать, что количество ядер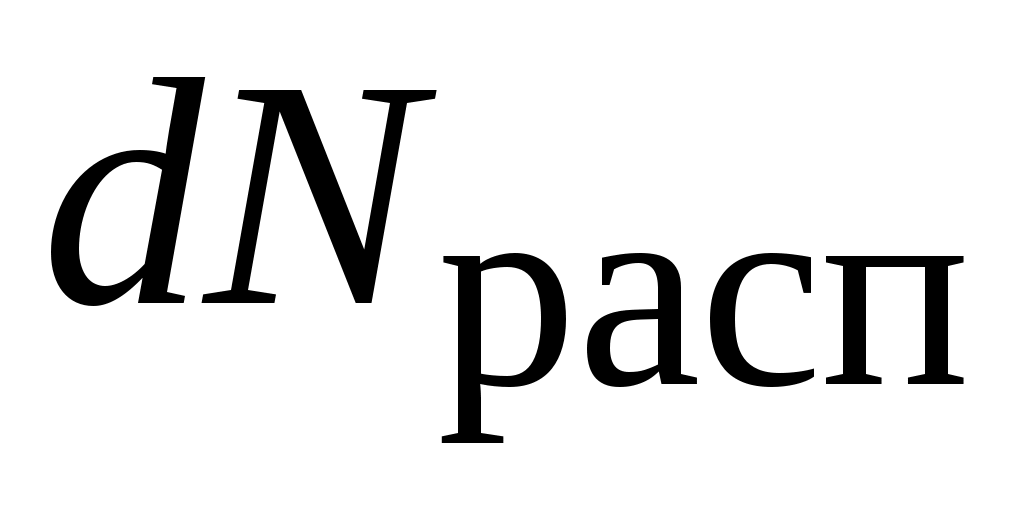 , распадающихся за очень короткий промежуток времени
, распадающихся за очень короткий промежуток времени  , пропорционально как числу имеющихся нераспавшихся ядер
, пропорционально как числу имеющихся нераспавшихся ядер  , так и этому промежутку времени
, так и этому промежутку времени 
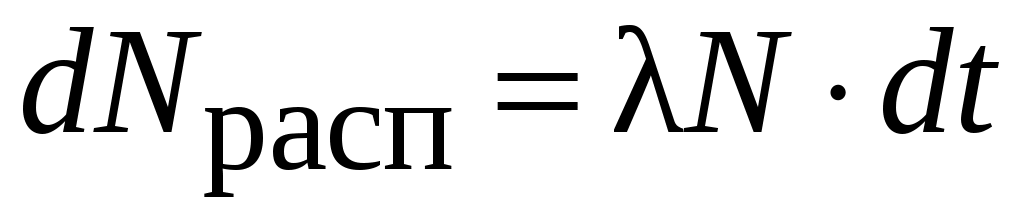 , (7.1)
, (7.1)
где – характерная для каждого радиоактивного вещества константа, называемая постоянной распада. Из формулы (7.1), переходя к одной переменной
– характерная для каждого радиоактивного вещества константа, называемая постоянной распада. Из формулы (7.1), переходя к одной переменной 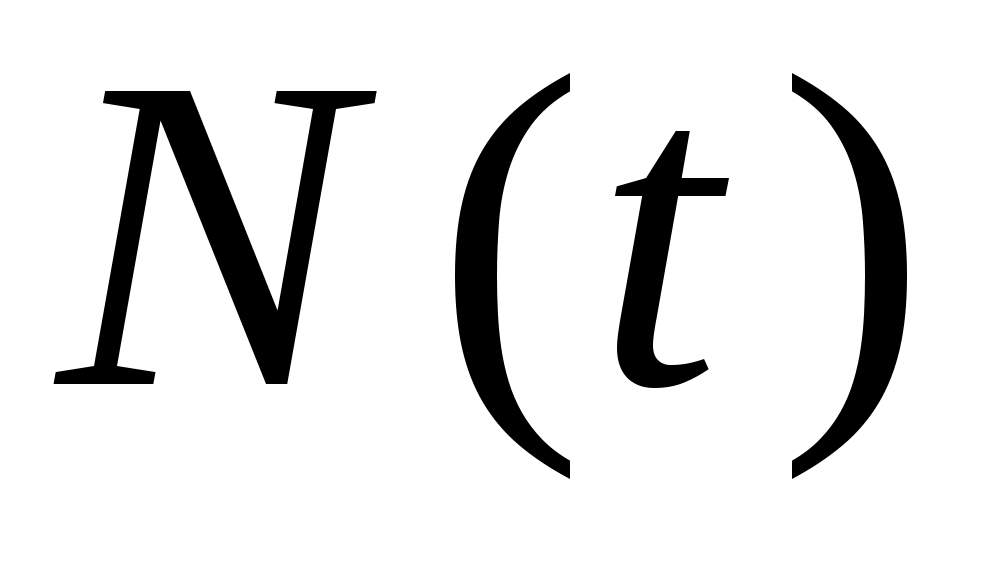 – количеству ядер, оставшихся нераспавшимися к моменту времени
– количеству ядер, оставшихся нераспавшимися к моменту времени 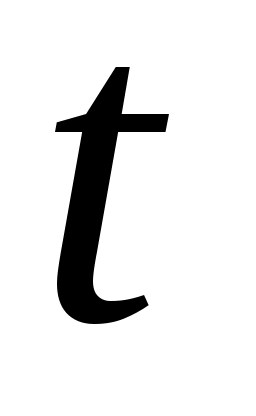 , и интегрируя, получаем закон радиоактивного распада, верный для любых, а не только малых, промежутков времени
, и интегрируя, получаем закон радиоактивного распада, верный для любых, а не только малых, промежутков времени
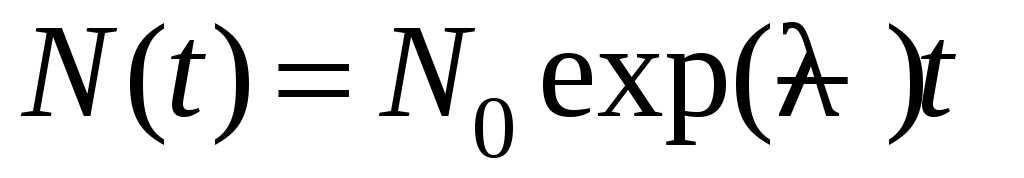 , (7.2)
, (7.2)
где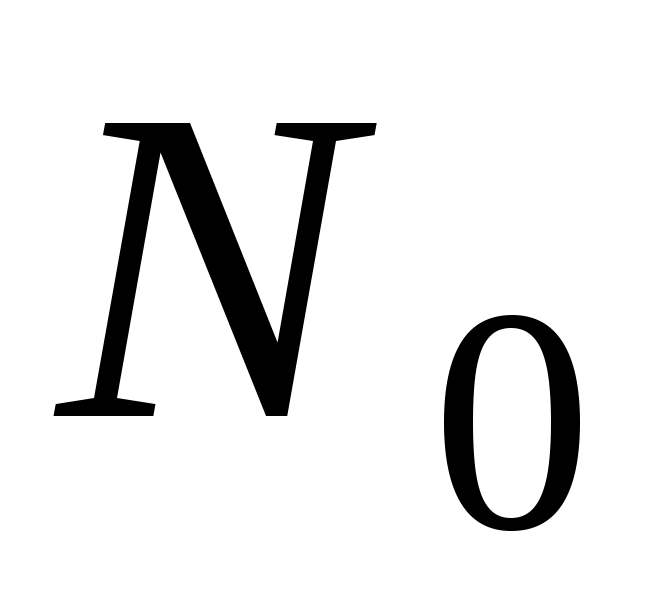 – количество ядер в первоначальный момент времени.
– количество ядер в первоначальный момент времени.
Время, за которое распадается половина первоначального количества ядер, называется периодом полураспада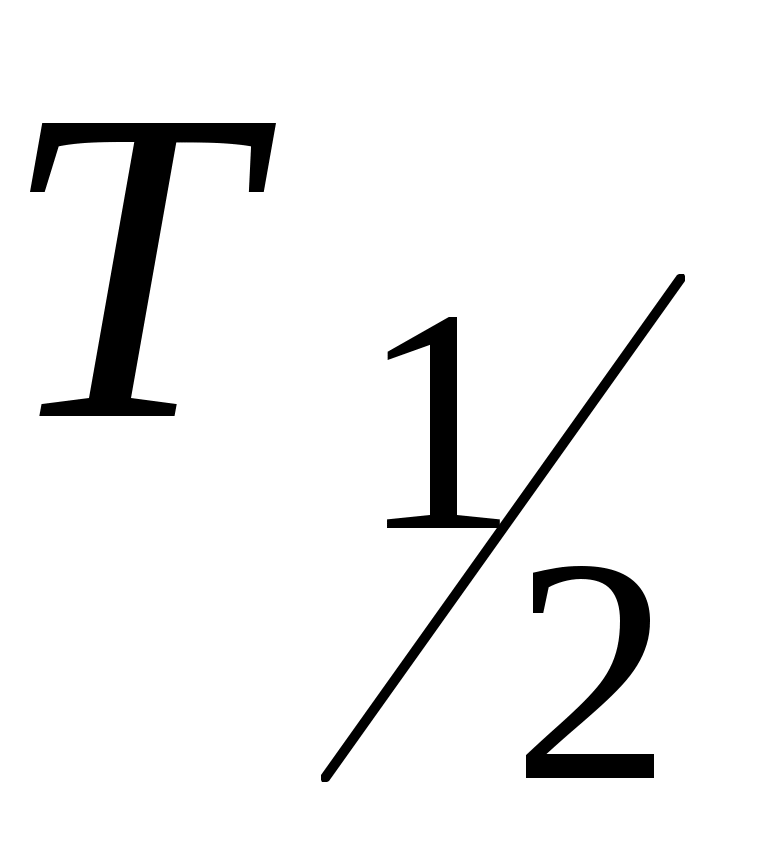 . Между этим временем и постоянной распада существует следующая связь:
. Между этим временем и постоянной распада существует следующая связь:
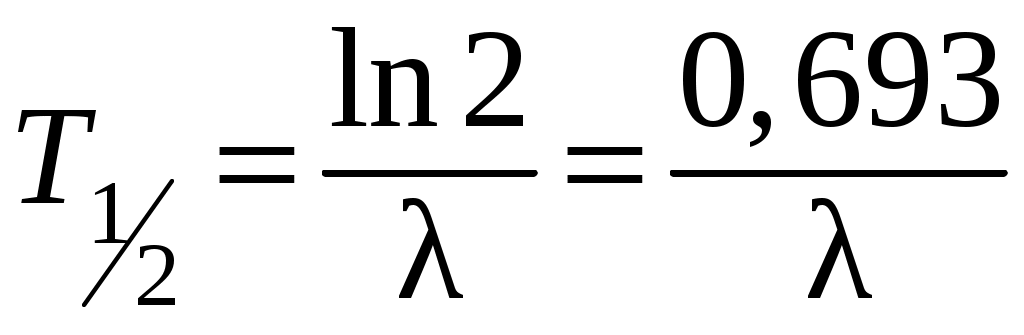 . (7.3)
. (7.3)
Активностью радиоактивного вещества называется величина, равная отношению числа распадов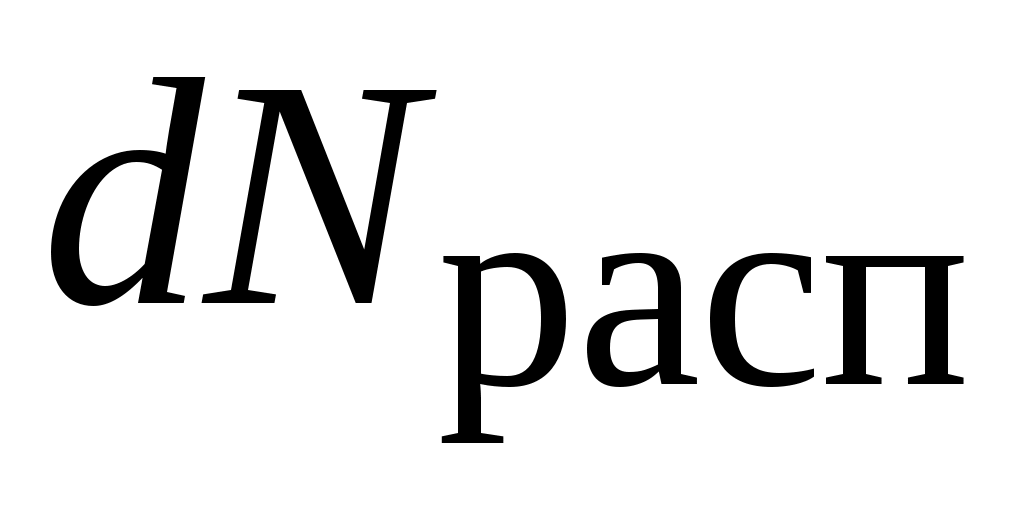 за малое время
за малое время 
Заметим, что вероятность заполнения уровня
Задача. Концентрация свободных электронов в металле равна
Дано:
Решение. Среднюю энергию найдем как отношение полной энергии свободных электронов в единице объема
При
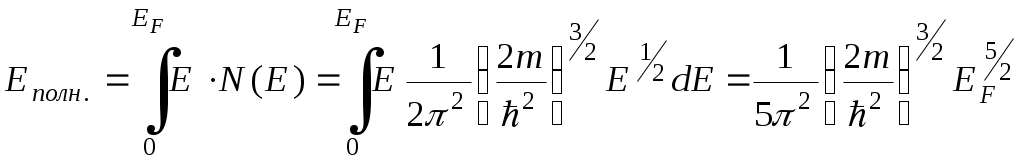 . (5.8)
. (5.8)Подставляя (5.8) в (5.7) и учитывая формулы (5.5), (5.6), находим
.
Проверяем единицу измерения
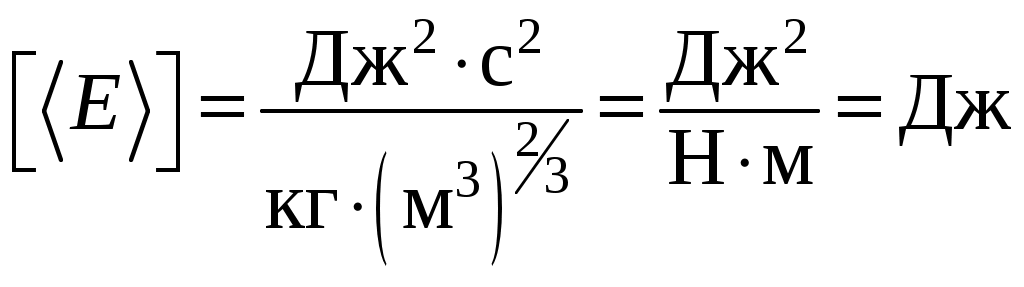 .
.Вычислим
Результат показывает, что с точки зрения квантовой теории электронный газ в металле при абсолютном нуле имеет энергию, которая соответствует температуре, в ее классическом понимании по порядку величины равной,
4. Рассмотрим элементы теории электропроводности собственных и примесных полупроводников.
Выше говорилось, что полупроводники при температуре
где
– подвижность электронов и дырок, которая характеризует среднюю дрейфовую скорость носителей тока под действием электрического поля единичной напряженности (
Уровень энергии Ферми в собственных полупроводниках расположен вблизи середины запрещенной зоны (рис. 5.4,а).

Рис. 5.4. Расположение уровня энергии Ферми и примесных уровней
в полупроводниках при температуре Т = 0 К:
а – собственный; б – донорный; в - акцепторный
Электропроводность собственных полупроводников увеличивается с ростом температуры
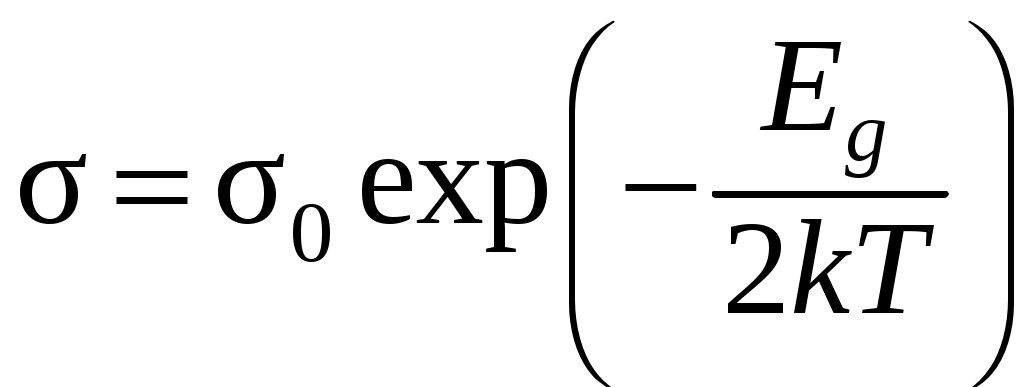 , (5.10)
, (5.10)где
Электропроводность примесных полупроводников обусловлена наличием в них примесных атомов, валентность которых больше (донорная примесь), или меньше (акцепторная примесь), чем у собственных атомов. Введение в собственный полупроводник примеси приводит к появлению в запрещенной зоне собственного полупроводника примесных уровней энергии. Для донорных полупроводников примесный уровень расположен вблизи дна зоны проводимости, а для акцепторных – вблизи потолка валентной зоны (рис. 5.4, б, в). Поскольку энергия активации примесей
Тип носителей тока и их концентрацию можно определить экспериментально с помощью эффекта Холла по знаку и величине постоянной Холла
Для полупроводника n-типа, у которого основными носителями тока являются электроны,
д
для собственного (n = p)
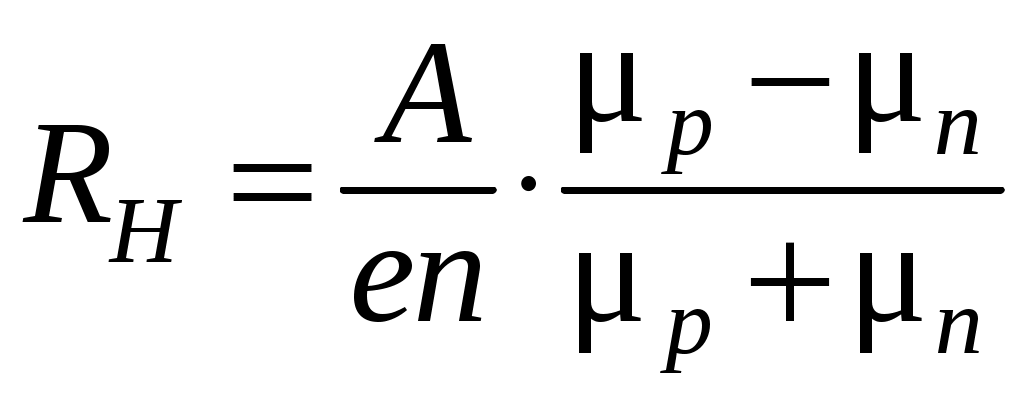 ,
,где
Дополнительные носители тока в полупроводниках могут возникать за счет поглощения света (фотонов). При этом, кроме удельной электропроводности, обусловленной тепловым возбуждением, появляется проводимость, обусловленная внутренним фотоэффектом,
В случае собственного полупроводника фотопроводимость
где
света.
Задача. Во сколько раз возрастет электропроводность образца кремния при нагревании его от температуры
Дано:
Решение. Зависимость электропроводности
 .
.Вычисляя с помощью этой формулы отношение электропроводностей при заданных температурах, получаем
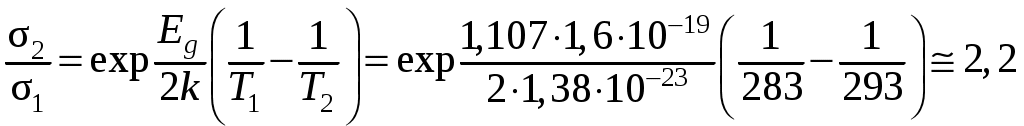 .
.Ответ. Электропроводность увеличится в 2,2 раза.
Тема 7.
ЯДЕРНЫЕ РЕАКЦИИ. РАДИОАКТИВНОСТЬ
Радиоактивностью называют самопроизвольное превращение одних атомных ядер в другие, сопровождаемое испусканием элементарных частиц.
Отдельные радиоактивные ядра претерпевают превращение независимо друг от друга. Поэтому можно считать, что количество ядер
где
где
Время, за которое распадается половина первоначального количества ядер, называется периодом полураспада
Активностью радиоактивного вещества называется величина, равная отношению числа распадов