ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 44
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| xi | Кол-во, fi | xi·fi | Накопленная частота, S | |x-x|·fi | (x-x)2·fi | Относительная частота, fi / f |
| 1 | 49.81 | 49.81 | 50 | 771.143 | 11938.595 | 0.0312 |
| 2 | 48.95 | 97.9 | 99 | 708.879 | 10265.76 | 0.0306 |
| 3 | 48.64 | 145.92 | 147 | 655.749 | 8840.609 | 0.0304 |
| 4 | 51.49 | 205.96 | 199 | 642.682 | 8021.759 | 0.0322 |
| 5 | 50.19 | 250.95 | 249 | 576.266 | 6616.506 | 0.0314 |
| 6 | 50.81 | 304.86 | 300 | 532.575 | 5582.281 | 0.0318 |
| 7 | 48.24 | 337.68 | 348 | 457.397 | 4336.893 | 0.0302 |
| 8 | 51.42 | 411.36 | 400 | 436.128 | 3699.106 | 0.0322 |
| 9 | 50.82 | 457.38 | 450 | 380.219 | 2844.683 | 0.0318 |
| 10 | 50.79 | 507.9 | 501 | 329.205 | 2133.804 | 0.0318 |
| 11 | 49.81 | 547.91 | 551 | 273.043 | 1496.736 | 0.0312 |
| 12 | 48.95 | 587.4 | 600 | 219.379 | 983.187 | 0.0306 |
| 13 | 48.8 | 634.4 | 649 | 169.906 | 591.561 | 0.0306 |
| 14 | 49.85 | 697.9 | 699 | 123.712 | 307.015 | 0.0312 |
| 15 | 50.5 | 757.5 | 749 | 74.825 | 110.868 | 0.0316 |
| 16 | 50.87 | 813.92 | 800 | 24.504 | 11.803 | 0.0318 |
| 17 | 49.93 | 848.81 | 850 | 25.879 | 13.414 | 0.0313 |
| 18 | 51.67 | 930.06 | 902 | 78.451 | 119.113 | 0.0323 |
| 19 | 51.2 | 972.8 | 953 | 128.938 | 324.705 | 0.0321 |
| 20 | 50.55 | 1011 | 1003 | 177.851 | 625.734 | 0.0316 |
| 21 | 49.14 | 1031.94 | 1052 | 222.03 | 1003.2 | 0.0308 |
| 22 | 48.37 | 1064.14 | 1101 | 266.921 | 1472.952 | 0.0303 |
| 23 | 48.81 | 1122.63 | 1150 | 318.159 | 2073.858 | 0.0306 |
| 24 | 48.51 | 1164.24 | 1198 | 364.713 | 2742.028 | 0.0304 |
| 25 | 50.55 | 1263.75 | 1249 | 430.601 | 3667.99 | 0.0316 |
| 26 | 49.32 | 1282.32 | 1298 | 469.443 | 4468.306 | 0.0309 |
| 27 | 49.93 | 1348.11 | 1348 | 525.179 | 5523.999 | 0.0313 |
| 28 | 50.81 | 1422.68 | 1399 | 585.245 | 6741.039 | 0.0318 |
| 29 | 51.08 | 1481.32 | 1450 | 639.435 | 8004.651 | 0.032 |
| 30 | 49.06 | 1471.8 | 1499 | 663.208 | 8965.457 | 0.0307 |
| 31 | 49.15 | 1523.65 | 1548 | 713.575 | 10359.904 | 0.0308 |
| 32 | 49.36 | 1579.52 | 1597 | 765.984 | 11886.776 | 0.0309 |
| Итого | 1597.38 | 26327.52 | | 12751.224 | 135774.289 | 1 |
Для оценки ряда распределения найдем следующие показатели:
Показатели центра распределения.
Средняя взвешенная (выборочная средняя)
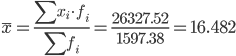
Мода.
Мода - наиболее часто встречающееся значение признака у единиц данной совокупности.
Максимальное значение повторений при x = 18 (f = 51.67). Следовательно, мода равна 18.
Медиана.
Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Находим xi, при котором накопленная частота S будет больше ∑f/2 = 799. Это значение xi = 16. Таким образом, медиана равна 16.
Медиана служит хорошей характеристикой при ассиметричном распределении данных, т.к. даже при наличии "выбросов" данных, медиана более устойчива к воздействию отклоняющихся данных.
В симметричных рядах распределения значение моды и медианы совпадают со средней величиной (xср=Me=Mo), а в умеренно асимметричных они соотносятся таким образом: 3(xср-Me) ≈ xср-Mo
Квартили.
Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q1, 25% будут заключены между Q1 и Q2, 25% - между Q2 и Q3. Остальные 25% превосходят Q3.
Находим xi, при котором накопленная частота S будет больше ∑f/4 = 399. Это значение xi = 8. Таким образом, первый квартиль равен 8.
25% единиц совокупности будут меньше по величине 8.
Q2 совпадает с медианой, Q2 = 16.
Находим x
i, при котором накопленная частота S будет больше 3/4∑f = 1198. Это значение xi = 24. Таким образом, третий квартиль равен 24.
Показатели вариации.
Абсолютные показатели вариации.
Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда.
R = xmax - xmin = 32 - 1 = 31
Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности.
Каждое значение ряда отличается от другого в среднем на 7.983
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
Несмещенная оценка дисперсии - состоятельная оценка дисперсии (исправленная дисперсия).
Среднее квадратическое отклонение.
Каждое значение ряда отличается от среднего значения 16.482 в среднем на 9.219
Оценка среднеквадратического отклонения.
Относительные показатели вариации.
К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение.
Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.
Поскольку v>30% ,но v<70%, то вариация умеренная.
Линейный коэффициент вариации или Относительное линейное отклонение - характеризует долю усредненного значения признака абсолютных отклонений от средней величины.
Коэффициент осцилляции - отражает относительную колеблемость крайних значений признака вокруг средней.
Показатели формы распределения.
Степень асимметрии.
Симметричным является распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой.
Наиболее точным и распространенным показателем асимметрии является моментный коэффициент асимметрии.
где M3 - центральный момент третьего порядка; s - среднеквадратическое отклонение.
M3 = 5300.46/1597.38 = 3.32
Положительная величина указывает на наличие правосторонней асимметрии
Оценка существенности показателя асимметрии дается с помощью средней квадратической ошибки коэффициента асимметрии:
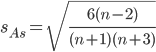
Если выполняется соотношение |As|/sAs < 3, то асимметрия несущественная, ее наличие объясняется влиянием различных случайных обстоятельств. Если имеет место соотношение |As|/sAs > 3, то асимметрия существенная и распределение признака в генеральной совокупности не является симметричным.
Расчет центральных моментов проводим в аналитической таблице:
| xi | (x-x)3·fi | (x-x)4·fi |
| 1 | -184829.607 | 2861474.443 |
| 2 | -148665.544 | 2152928.141 |
| 3 | -119186.333 | 1606833.043 |
| 4 | -100125.095 | 1249730.268 |
| 5 | -75968.667 | 872248.591 |
| 6 | -58511.735 | 613301.794 |
| 7 | -41121.068 | 389897.169 |
| 8 | -31374.663 | 266110.126 |
| 9 | -21283.036 | 159233.049 |
| 10 | -13830.655 | 89645.998 |
| 11 | -8204.643 | 44975.297 |
| 12 | -4406.338 | 19747.834 |
| 13 | -2059.632 | 7170.998 |
| 14 | -761.916 | 1890.838 |
| 15 | -164.272 | 243.399 |
| 16 | -5.685 | 2.739 |
| 17 | 6.952 | 3.603 |
| 18 | 180.851 | 274.588 |
| 19 | 817.708 | 2059.243 |
| 20 | 2201.527 | 7745.656 |
| 21 | 4532.769 | 20480.461 |
| 22 | 8128.205 | 44853.966 |
| 23 | 13518.051 | 88114.865 |
| 24 | 20615.419 | 154993.14 |
| 25 | 31245.082 | 266155.335 |
| 26 | 42530.724 | 404820.665 |
| 27 | 58103.142 | 611146.931 |
| 28 | 77645.381 | 894343.659 |
| 29 | 100204.707 | 1254393.712 |
| 30 | 121197.836 | 1638390.074 |
| 31 | 150408.309 | 2183674.645 |
| 32 | 184462.684 | 2862549.348 |
| Итого | 5300.462 | 20769433.616 |