ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 46
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
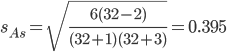
В анализируемом ряду распределения наблюдается несущественная асимметрия (0.00423/0.395 = 0.0107<3)
Применяются также структурные показатели (коэффициенты) асимметрии, характеризующие асимметрию только в центральной части распределения, т.е. основной массы единиц, и независящие от крайних значений признака. Рассчитаем структурный коэффициент асимметрии Пирсона:
Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения.
Чаще всего эксцесс оценивается с помощью показателя:
Для распределений более островершинных (вытянутых), чем нормальное, показатель эксцесса положительный (Ex > 0), для более плосковершинных (сплюснутых) - отрицательный (Ex < 0), т.к. для нормального распределения M4/s4 = 3.
M4
=
13002.19
Число 3 вычитается из отношения μ4/ σ4 потому, что для нормального закона распределения μ4/ σ4 = 3. Таким образом, для нормального распределения эксцесс равен нулю. Островершинные кривые обладают положительным эксцессом, кривые более плосковершинные - отрицательным эксцессом.
Ex < 0 - плосковершинное распределение
Чтобы оценить существенность эксцесса рассчитывают статистику Ex/sEx
где sEx - средняя квадратическая ошибка коэффициента эксцесса.
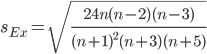
Если отношение Ex/sEx > 3, то отклонение от нормального распределения считается существенным.
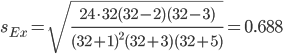
Ex/sEx = -1.2/0.688 = 1.743
Поскольку sEx < 3, то отклонение от нормального распределения считается не существенным.
Интервальное оценивание центра генеральной совокупности.
Доверительный интервал для генерального среднего.
В этом случае 2Ф(tkp) = γ
Ф(tkp) = γ/2 = 0.95/2 = 0.475
По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.475
tkp(γ) = (0.475) = 1.96
Стандартная ошибка выборки для среднего:
Стандартная ошибка среднего указывает, на сколько среднее выборки 16.482 отличается от среднего генеральной совокупности.
Предельная ошибка выборки:
или
ε = tkp sc = 1.96*0.231 = 0.452
Доверительный интервал:
(16.482 - 0.452;16.482 + 0.452) = (16.029;16.934)
С вероятностью 0.95 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.
Доверительный интервал для дисперсии.
Вероятность выхода за нижнюю границу равна P(χ2n-1 < hH) = γ/2 = 0.023. Для количества степеней свободы k=n-1=1596.38, по таблице распределения χ2 находим:
χ2(1596.38;0.023) = 241.0579.
Случайная ошибка дисперсии нижней границы:
Вероятность выхода за верхнюю границу равна P(χ2n-1 ≥ hB) = 1 - P(χ2n-1 < hH) = 1 - 0.023 = 0.977:
χ2(1596.38;0.977) = 156.432.
Случайная ошибка дисперсии верхней границы:
Таким образом, интервал (563.24;867.94) покрывает параметр S2 с надежностью α = 0.046 (γ=95.4%)
Доверительный интервал для среднеквадратического отклонения.
S*(1-q) < σ < S*(1+q)
Найдем доверительный интервал для среднеквадратического отклонения с надежностью γ = 0.954 и объему выборки n = 1597.38
По таблице q=q(γ ; n) определяем параметр q(0.954;1597.38) = 0
9.222(1-0) < σ < 9.222(1+0)
9.222 < σ < 9.222
Таким образом, интервал (9.222;9.222) покрывает параметр σ с надежностью γ = 0.954
Интервальное оценивание генеральной доли (вероятности события).
Доверительный интервал для генеральной доли.
(p* - ε ; p* + ε)
В этом случае 2Ф(tkp) = γ
Ф(tkp) = γ/2 = 0.954/2 = 0.477
По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.477
tkp(γ) = (0.477) = 2
| Доля i-ой группы fi / ∑f | Средняя ошибка выборки для генеральной доли, ε | Нижняя граница доли, p* - ε | Верхняя граница доли, p* + ε |
| 0.03118 | | 0 | 0 |
| 0.03064 | | 0 | 0 |
| 0.03045 | | 0 | 0 |
| 0.03223 | | 0 | 0 |
| 0.03142 | | 0 | 0 |
| 0.03181 | | 0 | 0 |
| 0.0302 | | 0 | 0 |
| 0.03219 | | 0 | 0 |
| 0.03181 | | 0 | 0 |
| 0.0318 | | 0 | 0 |
| 0.03118 | | 0 | 0 |
| 0.03064 | | 0 | 0 |
| 0.03055 | | 0 | 0 |
| 0.03121 | | 0 | 0 |
| 0.03161 | | 0 | 0 |
| 0.03185 | | 0 | 0 |
| 0.03126 | | 0 | 0 |
| 0.03235 | | 0 | 0 |
| 0.03205 | | 0 | 0 |
| 0.03165 | | 0 | 0 |
| 0.03076 | | 0 | 0 |
| 0.03028 | | 0 | 0 |
| 0.03056 | | 0 | 0 |
| 0.03037 | | 0 | 0 |
| 0.03165 | | 0 | 0 |
| 0.03088 | | 0 | 0 |
| 0.03126 | | 0 | 0 |
| 0.03181 | | 0 | 0 |
| 0.03198 | | 0 | 0 |
| 0.03071 | | 0 | 0 |
| 0.03077 | | 0 | 0 |
| 0.0309 | | 0 | 0 |
С вероятностью 0.954 при большем объеме выборке эти доли будут находиться в заданных интервалах.
Проверка гипотез о виде распределения.
1. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.
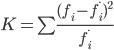
где f*i - теоретические частоты:
Вычислим теоретические частоты, учитывая, что:
N = 1597.38, h=1 (ширина интервала), σ = 9.219, xср = 16.482
| i | xi | ui | φi | fi* |
| 1 | 1 | -1.6792 | 0,0973 | 16.858 |
| 2 | 2 | -1.5708 | 0,1145 | 19.839 |
| 3 | 3 | -1.4623 | 0,1354 | 23.46 |
| 4 | 4 | -1.3538 | 0,1582 | 27.41 |
| 5 | 5 | -1.2454 | 0,1826 | 31.638 |
| 6 | 6 | -1.1369 | 0,2083 | 36.09 |
| 7 | 7 | -1.0284 | 0,2347 | 40.665 |
| 8 | 8 | -0.92 | 0,2613 | 45.273 |
| 9 | 9 | -0.8115 | 0,285 | 49.38 |
| 10 | 10 | -0.703 | 0,3101 | 53.729 |
| 11 | 11 | -0.5946 | 0,3332 | 57.731 |
| 12 | 12 | -0.4861 | 0,3538 | 61.3 |
| 13 | 13 | -0.3776 | 0,3712 | 64.315 |
| 14 | 14 | -0.2692 | 0,3847 | 66.654 |
| 15 | 15 | -0.1607 | 0,3932 | 68.127 |
| 16 | 16 | -0.05225 | 0,3982 | 68.993 |
| 17 | 17 | 0.05622 | 0,3982 | 68.993 |
| 18 | 18 | 0.1647 | 0,3932 | 68.127 |
| 19 | 19 | 0.2732 | 0,3825 | 66.273 |
| 20 | 20 | 0.3816 | 0,3697 | 64.055 |
| 21 | 21 | 0.4901 | 0,3521 | 61.006 |
| 22 | 22 | 0.5986 | 0,3332 | 57.731 |
| 23 | 23 | 0.707 | 0,3101 | 53.729 |
| 24 | 24 | 0.8155 | 0,285 | 49.38 |
| 25 | 25 | 0.924 | 0,2589 | 44.858 |
| 26 | 26 | 1.0324 | 0,2323 | 40.249 |
| 27 | 27 | 1.1409 | 0,2059 | 35.675 |
| 28 | 28 | 1.2494 | 0,1826 | 31.638 |
| 29 | 29 | 1.3578 | 0,1582 | 27.41 |
| 30 | 30 | 1.4663 | 0,1354 | 23.46 |
| 31 | 31 | 1.5747 | 0,1145 | 19.839 |
| 32 | 32 | 1.6832 | 0,0957 | 16.581 |