ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 48
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
равномерного распределения по формулам:

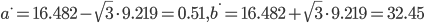
2. Найдем плотность предполагаемого равномерного распределения:
f(x) = 1/(b* - a*) = 1/(32.45 - 0.51) = 0.0313
3. Найдем теоретические частоты:
n1 = n*f(x)(x1 - a*) = 1597.38 * 0.0313(1-0.51) = 24.35
n32 = n*f(x)(b* - x31) = 1597.38 * 0.0313(32.45-32) = 22.52
Остальные ns будут равны:
ns = n*f(x)(xi - xi-1)
Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение Kнабл, тем сильнее довод против основной гипотезы.
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения χ2 и заданным значениям s, k (число интервалов), r=2 (параметры a и b).
Kkp(29,0.05) = 42.55697; Kнабл = 59.25
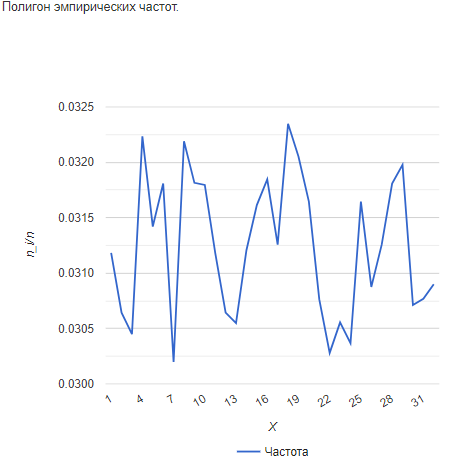
Наблюдаемое значение статистики Пирсона попадает в критическую область: Кнабл > Kkp, поэтому есть основания отвергать основную гипотезу. Данные выборки распределены не по равномерному закону.
Выводы:
Каждое значение ряда отличается от среднего значения 16.482 в среднем на 9.219.
Среднее значение примерно равно моде и медиане, что свидетельствует о нормальном распределении выборки.
Поскольку коэффициент вариации находится в пределах [30%; 70%], то вариация умеренная.
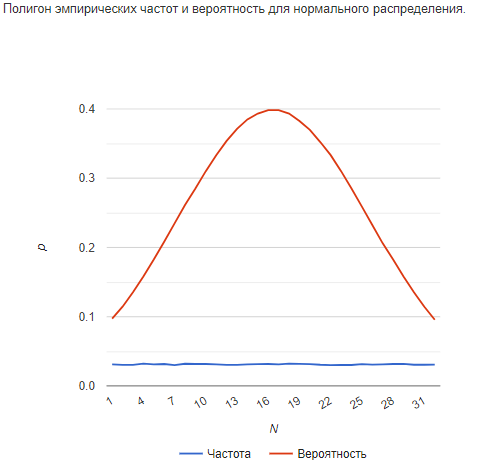
Гипотеза о том, что случайная величина Х подчинена нормальному закону распределения, отвергается (по критерию согласия Пирсона).
Значения As и Ex мало отличаются от нуля. Поэтому можно предположить близость данной выборки к нормальному распределению.
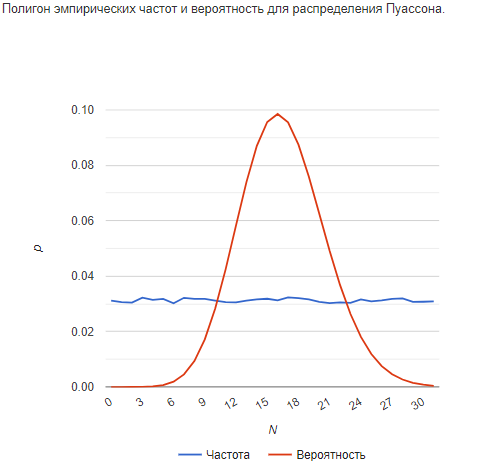
Наблюдаемое значение статистики Пирсона попадает в критическую область: Кнабл > Kkp, поэтому есть основания отвергать основную гипотезу. Данные выборки распределены не по закону Пуассона.
2. Найдем плотность предполагаемого равномерного распределения:
f(x) = 1/(b* - a*) = 1/(32.45 - 0.51) = 0.0313
3. Найдем теоретические частоты:
n1 = n*f(x)(x1 - a*) = 1597.38 * 0.0313(1-0.51) = 24.35
n32 = n*f(x)(b* - x31) = 1597.38 * 0.0313(32.45-32) = 22.52
Остальные ns будут равны:
ns = n*f(x)(xi - xi-1)
| i | ni | n*i | ni - n*i | (ni - n*i)2 | (ni - n*i)2/n*i |
| 1 | 50 | 24.3507 | 25.4593 | 648.1762 | 26.6184 |
| 2 | 49 | 50.0165 | -1.0665 | 1.1373 | 0.02274 |
| 3 | 49 | 50.0165 | -1.3765 | 1.8946 | 0.03788 |
| 4 | 51 | 50.0165 | 1.4735 | 2.1713 | 0.04341 |
| 5 | 50 | 50.0165 | 0.1735 | 0.03012 | 0.000602 |
| 6 | 51 | 50.0165 | 0.7935 | 0.6297 | 0.01259 |
| 7 | 48 | 50.0165 | -1.7765 | 3.1558 | 0.0631 |
| 8 | 51 | 50.0165 | 1.4035 | 1.9699 | 0.03939 |
| 9 | 51 | 50.0165 | 0.8035 | 0.6457 | 0.01291 |
| 10 | 51 | 50.0165 | 0.7735 | 0.5984 | 0.01196 |
| 11 | 50 | 50.0165 | -0.2065 | 0.04263 | 0.000852 |
| 12 | 49 | 50.0165 | -1.0665 | 1.1373 | 0.02274 |
| 13 | 49 | 50.0165 | -1.2165 | 1.4798 | 0.02959 |
| 14 | 50 | 50.0165 | -0.1665 | 0.02771 | 0.000554 |
| 15 | 51 | 50.0165 | 0.4835 | 0.2338 | 0.00467 |
| 16 | 51 | 50.0165 | 0.8535 | 0.7285 | 0.01457 |
| 17 | 50 | 50.0165 | -0.08646 | 0.00748 | 0.000149 |
| 18 | 52 | 50.0165 | 1.6535 | 2.7342 | 0.05467 |
| 19 | 51 | 50.0165 | 1.1835 | 1.4008 | 0.02801 |
| 20 | 51 | 50.0165 | 0.5335 | 0.2847 | 0.00569 |
| 21 | 49 | 50.0165 | -0.8765 | 0.7682 | 0.01536 |
| 22 | 48 | 50.0165 | -1.6465 | 2.7108 | 0.0542 |
| 23 | 49 | 50.0165 | -1.2065 | 1.4556 | 0.0291 |
| 24 | 49 | 50.0165 | -1.5065 | 2.2694 | 0.04537 |
| 25 | 51 | 50.0165 | 0.5335 | 0.2847 | 0.00569 |
| 26 | 49 | 50.0165 | -0.6965 | 0.4851 | 0.0097 |
| 27 | 50 | 50.0165 | -0.08646 | 0.00748 | 0.000149 |
| 28 | 51 | 50.0165 | 0.7935 | 0.6297 | 0.01259 |
| 29 | 51 | 50.0165 | 1.0635 | 1.1311 | 0.02261 |
| 30 | 49 | 50.0165 | -0.9565 | 0.9148 | 0.01829 |
| 31 | 49 | 50.0165 | -0.8665 | 0.7508 | 0.01501 |
| 32 | 49 | 22.519 | 26.841 | 720.4409 | 31.9926 |
| Итого | 1597 | | | | 59.2451 |
Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение Kнабл, тем сильнее довод против основной гипотезы.
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения χ2 и заданным значениям s, k (число интервалов), r=2 (параметры a и b).
Kkp(29,0.05) = 42.55697; Kнабл = 59.25
Наблюдаемое значение статистики Пирсона попадает в критическую область: Кнабл > Kkp, поэтому есть основания отвергать основную гипотезу. Данные выборки распределены не по равномерному закону.
Выводы:
Каждое значение ряда отличается от среднего значения 16.482 в среднем на 9.219.
Среднее значение примерно равно моде и медиане, что свидетельствует о нормальном распределении выборки.
Поскольку коэффициент вариации находится в пределах [30%; 70%], то вариация умеренная.
Гипотеза о том, что случайная величина Х подчинена нормальному закону распределения, отвергается (по критерию согласия Пирсона).
Значения As и Ex мало отличаются от нуля. Поэтому можно предположить близость данной выборки к нормальному распределению.
Наблюдаемое значение статистики Пирсона попадает в критическую область: Кнабл > Kkp, поэтому есть основания отвергать основную гипотезу. Данные выборки распределены не по закону Пуассона.


