8.3. Зубчатые передачи. Виды и классификация
Зубчатые передачи осуществляют передачу вращательного движения с одного вала на другой с помощью цилиндрических, конических, червячных колёс, имеющих специально профилированные зубья, при этом зубчатые колёса могут иметь прямые, косые, спиральные, шевронные зубья и др. (рис. 65).



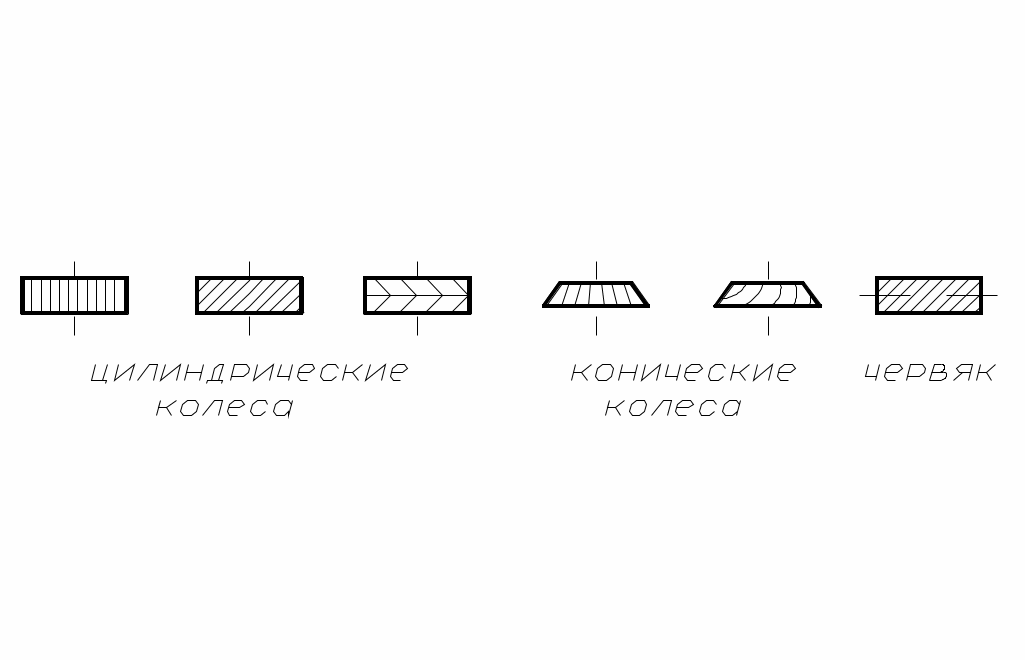
рис. 65

При использовании непрямозубых колёс повышается плавность и бесшумность работы и увеличивается нагрузочная способность передачи.

В зубчатых передачах с пересекающимися осями в качестве начальных поверхностей используются усечённые конусы, вершины которых пересекаются в одной точке (рис. 66, а), а в передачах с перекрещивающимися осями теоретическими начальными поверхностями являются гиперболоиды вращения (рис. 66,б). Такие передачи называются гиперболоидными.



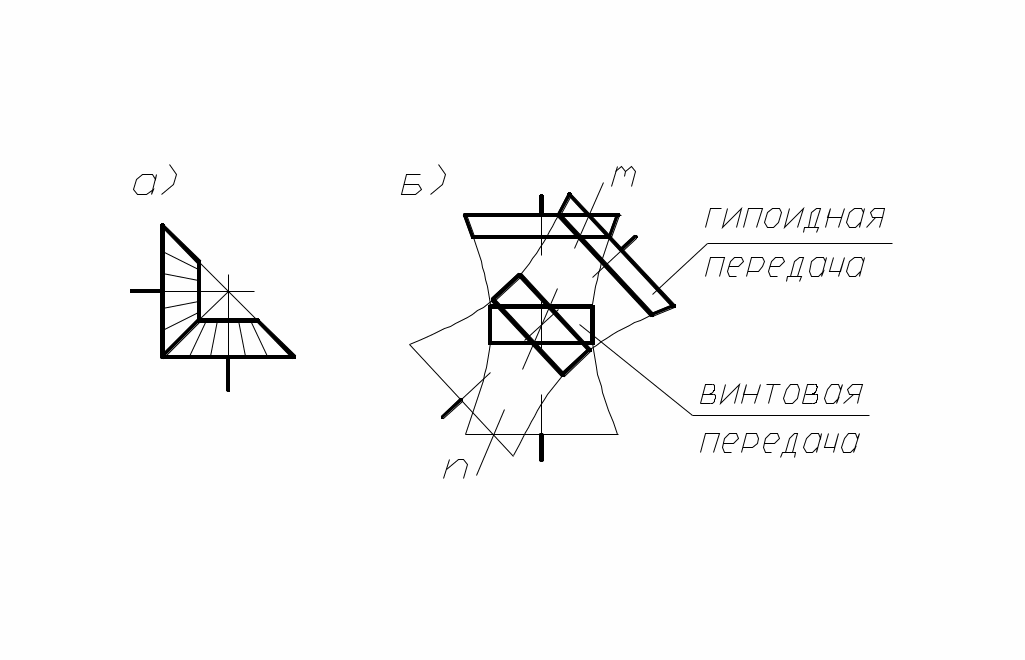
рис. 66
Контакт зубьев 2-х колёс в таких передачах происходит по прямолинейным образующим mn. В машиностроительной практике ограничиваются отдельными короткими частями гиперболоидов. Например, используя среднюю часть гиперболоидов, получают винтовую зубчатую передачу, а если использовать усечённые конусы, близкие по профилю к гиперболоидам в их широкой части, то получим так называемую гипоидную передачу (рис. 66, б).

Частным случаем винтовой передачи является червячная передача, в которой малое колесо называется червяком, а большое – червячным колесом (рис. 67, а, б).



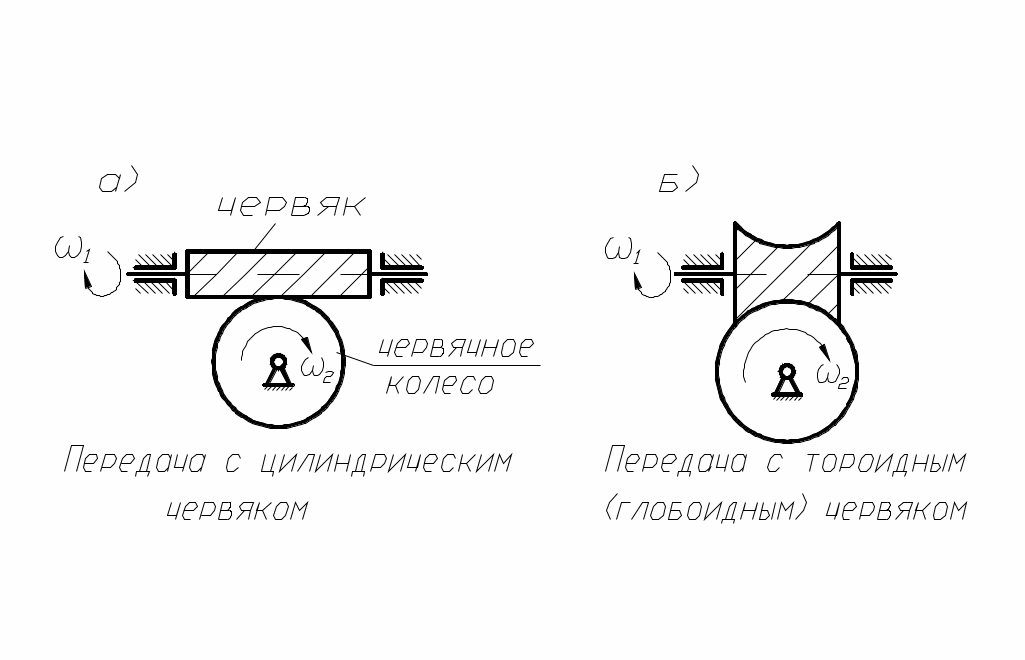
рис. 67
Червячные передачи могут быть с одно и многозаходными червяками, при этом число заходов червяка равно числу его зубьев.

Червячные передачи позволяют обеспечить большое передаточное отношение при сравнительно малых габаритах вследствие малого числа зубьев (заходов) на червяке, т. к. (Z₁, Z₂ – число зубьев колёс). Однако коэффициент полезного действия (КПД) передачи низок.

Предельные значения передаточных отношений для зубчатой пары составляет:

• 
  1…6 – для цилиндрических передач;
  
• 
  1…4 – для конических передач;
  
• 
  10…40 – для червячно-винтовых передач.
  

---

По форме профиля зуба различают передачи эвольвентные, циклоидальные, цевочные, а также передачи с зацеплением Новикова.

Наибольшее распространение получили эвольвентные передачи с профилем, предложенным Леонардом Эйлером в 1754 г. Преимуществом этого профиля является простота изготовления, достаточно высокая нагрузочная способность, малая чувствительность к неточностям межцентрового расстояния. Однако эвольвентный профиль удовлетворяет не всем требованиям, предъявляемым к современным зубчатым передачам. Так, например, в мощных передачах внешнего зацепления, где контактируют выпуклые зубья с малыми радиусами кривизны профилей, происходит их быстрое разрушение из-за недостаточной контактной прочности. Одним из путей повышения контактной прочности является использование внутреннего зацепления, в котором профиль зуба одного из колёс вогнут ый. Другой путь – применение передач с зацеплением Новикова, где выпуклые профили зубьев одного из колёс, очерченные по дуге окружности, контактируют в вогнутыми профилями другого колеса (рис. 68). При этом нагрузочная способность передачи повышается в 2-3 раза по сравнению с эвольвентной, а также уменьшаются потери на трение.

рис. 68

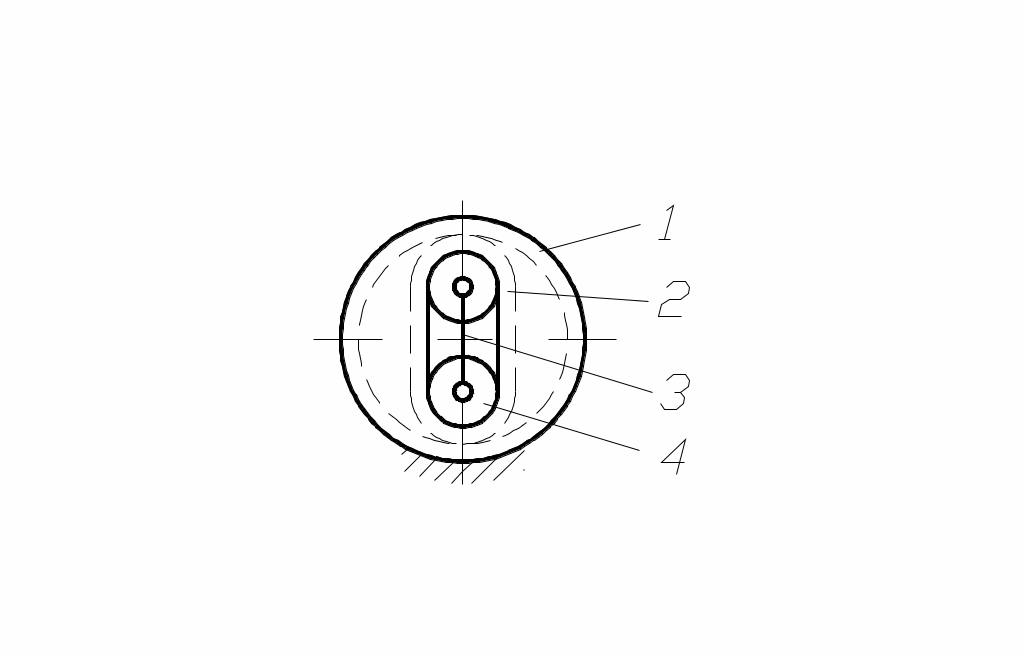Одной из интересных и перспективных передач является так называемая волновая передача (рис. 69), состоящая из жёсткого 1 и гибкого 2 зубчатых колёс, а также генератора волн 3 с роликами 4. При вращении генератора 3, благодаря разнице чисел зубьев жёсткого и гибкого колёс, приводится во вращение колесо 2, причём передаточное отношение может быть очень большим ( ). Автор волновой передачи – Массер (США, 1959 г.) указывал на возможность использования треугольного профиля зубьев.

рис. 69

К зубчатым передачам относятся передачи с некруглыми, секторными колёсами, колёсами, имеющими зубья на части обода и др.

Обычно в зубчатых передачах меньшее колесо называется шестерней.

Выбор той или иной передачи зависит от традиционной области её применения и конкретных функциональных особенностей механизма, в котором эта передача будет использована.
8.4. Основная теорема зацепления (теорема Виллиса)

---

Для постоянства передаточного отношения при зацеплении двух профилей зубьев необходимо, чтобы радиусы начальных окружностей зубчатых колёс, перекатывающихся друг по другу без скольжения, оставались неизменными. Если рассмотреть обращённое движение начальных окружностей, когда всей системе задана угловая скорость ( ), то второе колесо будет условно неподвижным и точка Р является мгновенным центром относительного вращения колёс (рис. 70,а). Эта точка, называемая полюсом зацепления, где контактируют начальные окружности, делит межцентровое расстояние на отрезки, обратно пропорциональные угловым скоростям, т. к.

.

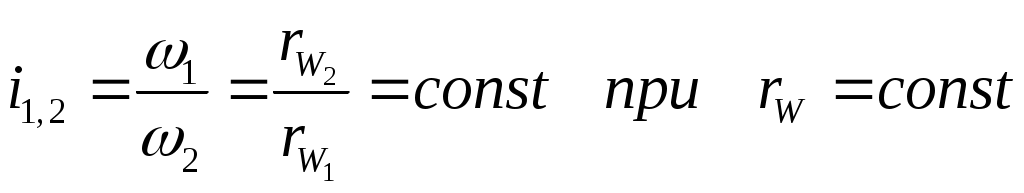Рассмотрим обращённое движение профилей зубьев зубчатых колёс (рис. 70, б).



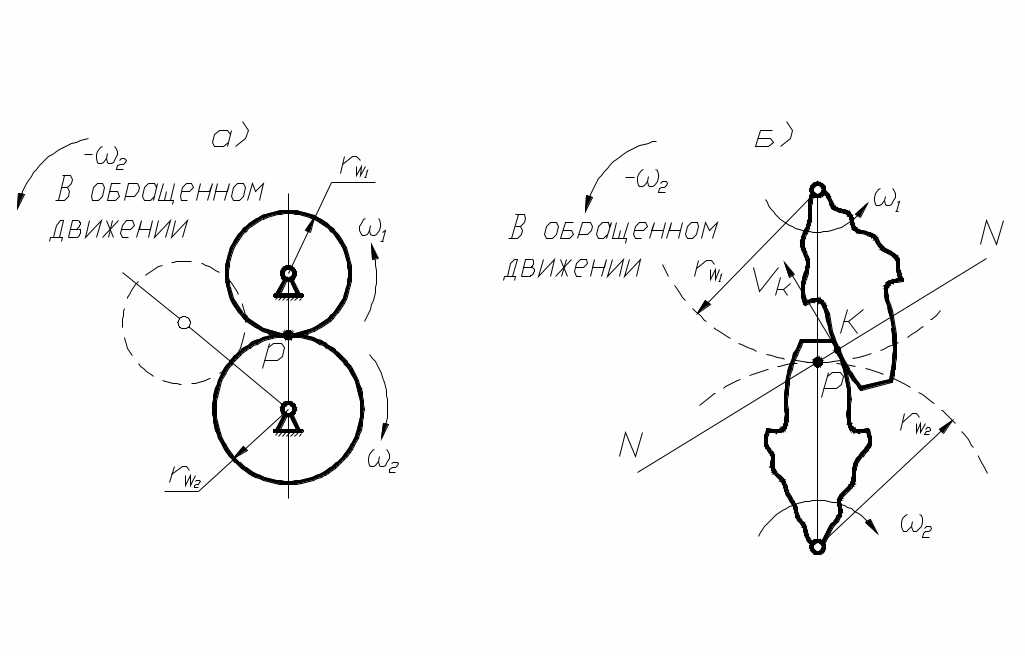
рис. 70

Точка контакта зубьев (точка к), принадлежащая первому колесу, вращается вокруг точки Р, которая будет мгновенным центром скоростей. Скорость и совпадает с общей касательной к профилям в точке к при условии постоянства этого контакта.

В противном случае постоянного контакта не будет, так как появится составляющая и профили разомкнутся (рис. 71). Так как рассматривается произвольное положение зубьев, то можно сформулировать теорему.

Нормаль NN к касающимся профилям зубьев,

рис. 71 проведённая через точку их касания, делит межцентровое расстояние на части, обратно пропорциональные угловым скоростям.

Эта теорема, сформулированная Виллисом в 1841 г., определяет основной закон зацепления профилей, которые не могут быть произвольными, а должны быть специально подобраны.

8.5. Эвольвента и её свойства




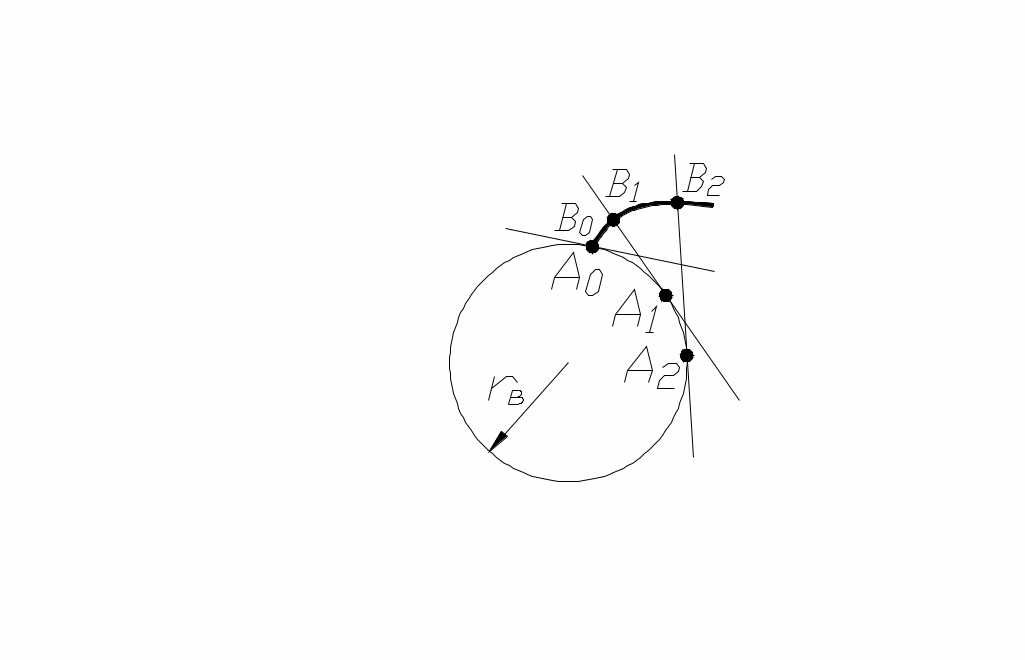
Наибольшее применение получили эвольвентные зубчатые передачи с профилем зубьев, очерченным по эвольвенте (рис. 72).

---

Эвольвентой круга называется траектория точки, лежащей на прямой, которая перекатывается без скольжения по окружности радиуса r_в, называемой основной.

рис. 72

Эвольвента имеет следующие свойства:

1) начинается с основной окружности;

2) нормаль к эвольвенте является касательной к основной окружности;

3) радиус кривизны эвольвенты в каждой её точке лежит на нормали к эвольвенте в этой точке.

Основная окружность представляет собой геометрическое место центров кривизны эвольвенты и является её эволютой.
8.6. Геометрия эвольвентного зацепления
В 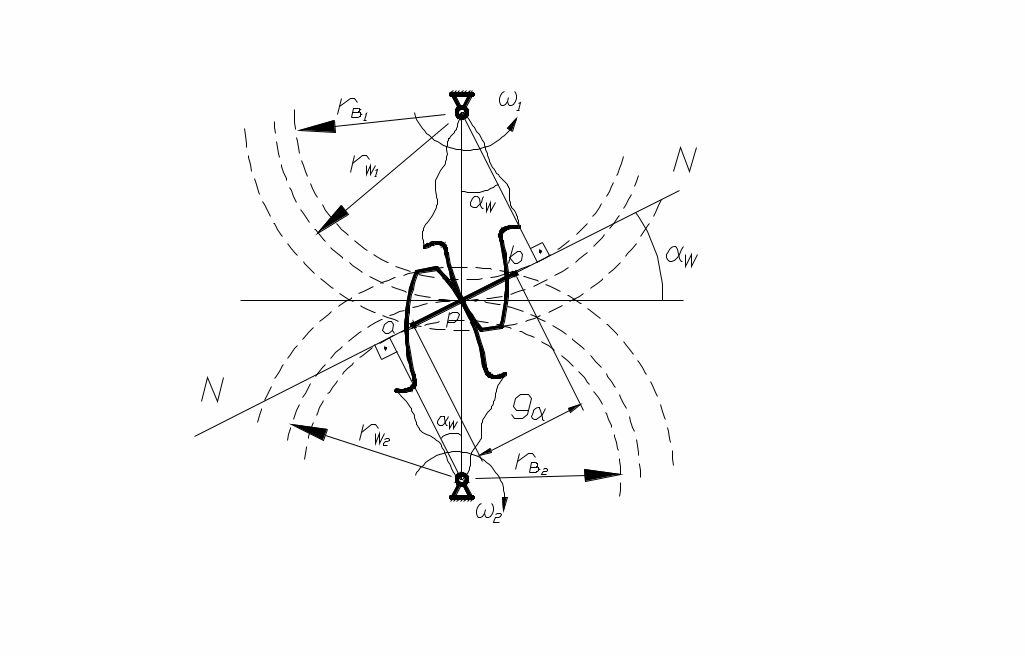процессе зацепления зубья касаются друг друга различными точками профиля (рис. 73). Так как эти точки лежат на нормали к профилям, которая одновременно является касательной к обеим основным окружностям, то совокупность точек касания (линия ) совпадает с общей для обеих основных окружностей касательной NN. Эта линия называется теоретической линией зацепления, а линия длиной g_α является её активной частью, где располагаются все точки контакта зубьев. Угол , измеряемый между нормалью NN к профилям в полюсе

рис. 73 зацепления Р и общей касательной к обеим начальным окружностям, называется углом зацепления. Таким образом:

; .
8.7. Качественные показатели зацепления
Одним из качественных показателей зубчатой передачи является коэффициент перекрытия , равный , где р_в – шаг по основной окружности (расстояние между одноимёнными точками двух соседних зубьев, замеренное по дуге основной окружности). Коэффициент

---

показывает сколько пар зубьев в среднем одновременно находится в зацеплении. Для прямозубой передачи обычно . Чем больше , тем более плавно и бесшумно работает передача.

Другим качественным показателем является коэффициент скольжения, который учитывает влияние геометрии передачи и её кинематики на скольжение и износ профилей, скользящих друг по другу (рис. 74), что видно из картины скоростей. На этой картине:

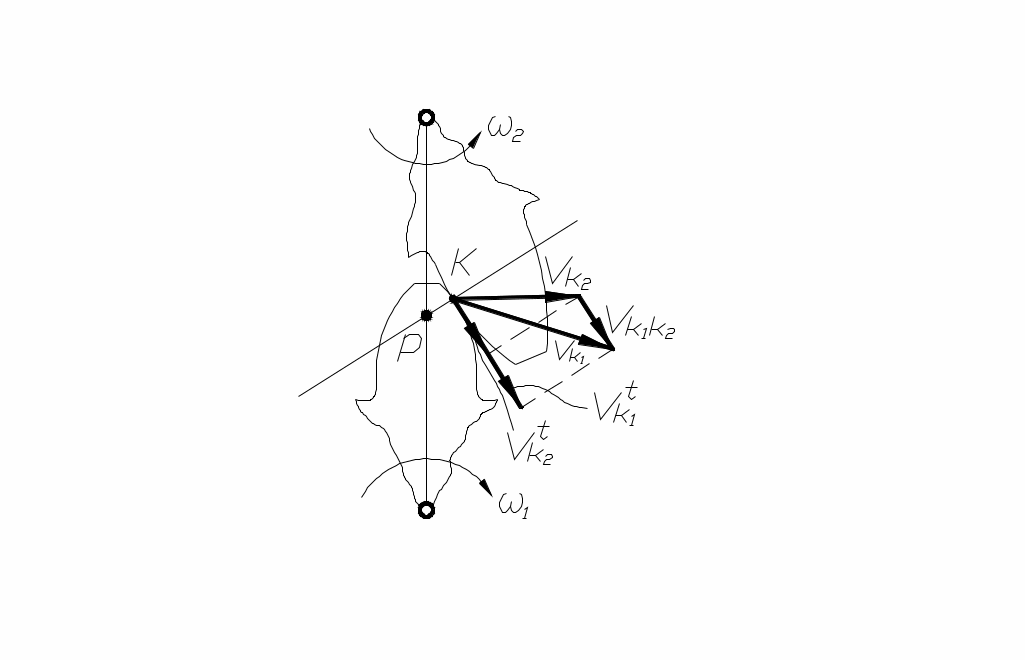- скорость точки к первого колеса;

- проекция этой скорости на касательную к контактирующим профилям;

и - тоже для колеса 2.

Скорость скольжения колеса 1 и 2 относительно друг друга равна:

.

Коэффициенты скольжения колёс 1 и 2 равны:

; .

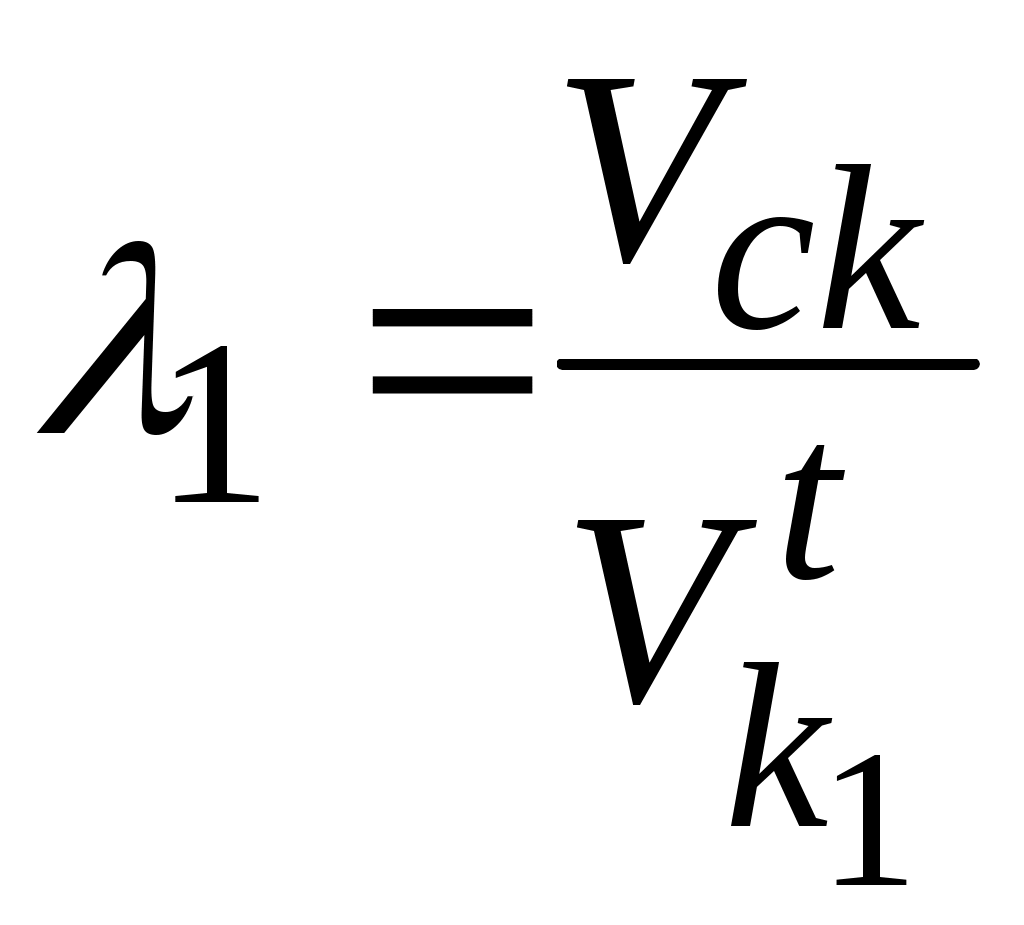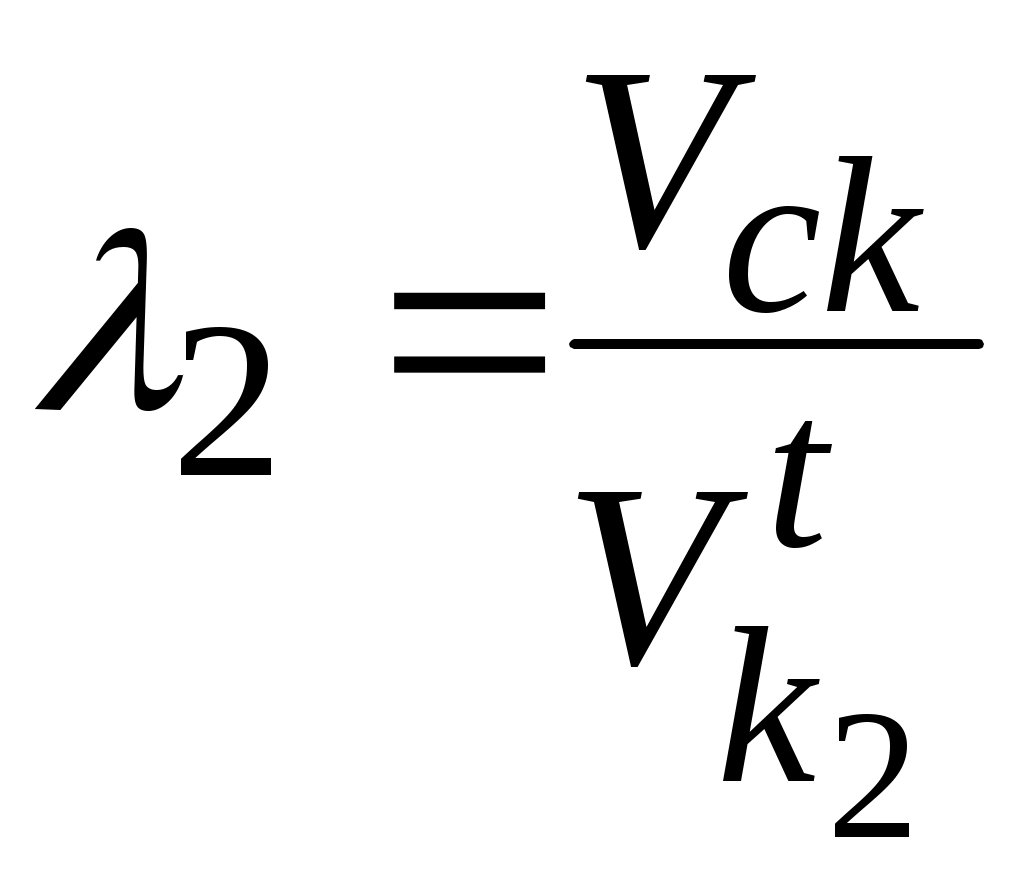Эти коэффициенты равны нулю в полюсе (точка Р) и увеличиваются с удалением от не-

рис. 74 го по линии зацепления.

Таким образом, чем длиннее линия зацепления, (то есть, чем больше коэффициент перекрытия ), тем больше скольжение и износ профилей зубьев.
8.8. Основные параметры зубчатых колёс
О 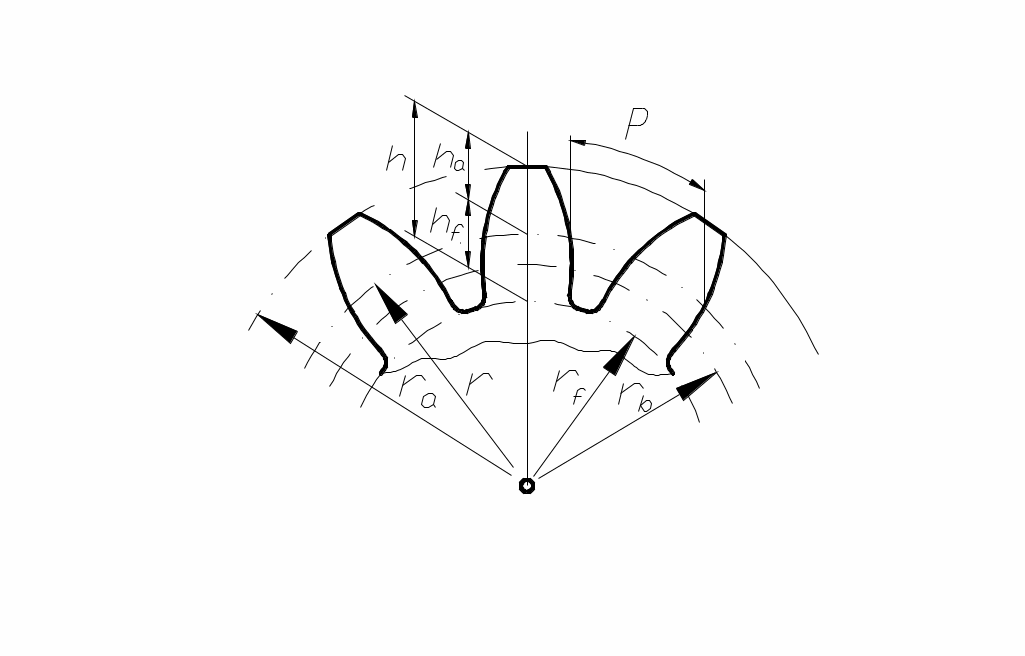сновными параметрами зубчатого колеса являются (рис. 75):

z – число зубьев;

r_a – радиус (диаметр) окружности

выступов;

r_f – радиус (диаметр) окружности

впадин;

r_b - радиус (диаметр) основной окружности;

r - радиус (диаметр) делительной

рис. 75 окружности, т. е. окружности, ко-

---

Смотрите также файлы

• Новостная справка за прошедшую неделю о событиях на Донбассе.docx

• Цель занятия закрепление знаний о нормативноправовых основах взаимодействии воспитателя с сотрудниками детского сада, формирование умения применять полученные знания на практике Задание 1.docx

• Guardians of Cloudia.docx

• "политика".docx

• Вавававававававакваапмвпвапвававававававававававаавваваававвааылзщвчсвва.docx