Файл: Оглавление Введение Основные понятия и определения тмм.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 150
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
) путём графического дифферен-
цирования графиков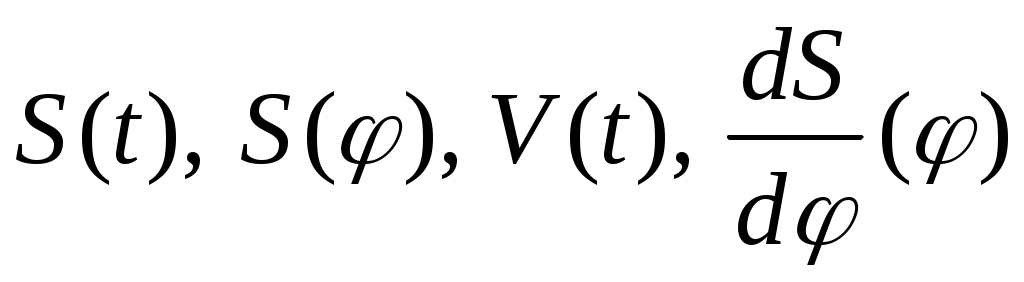 .
.
Движение толкателя имеет реверсивный характер за весь кинематический цикл, при этом наблюдаются 4 фазы движения толкателя, соответствующие 4 фазовым углам поворота кулачка: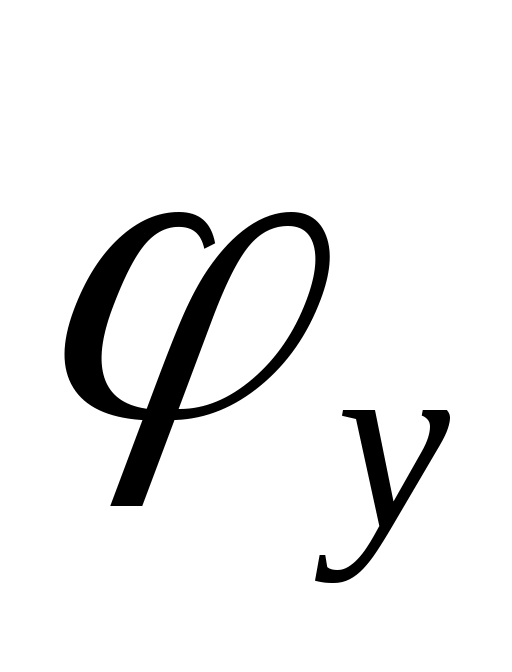 - угол удаления (подъёма) толкателя;
- угол удаления (подъёма) толкателя; 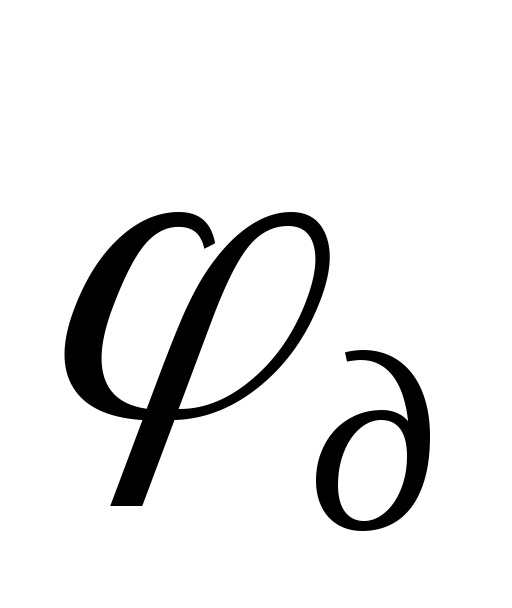 - угол дальнего выстоя;
- угол дальнего выстоя; 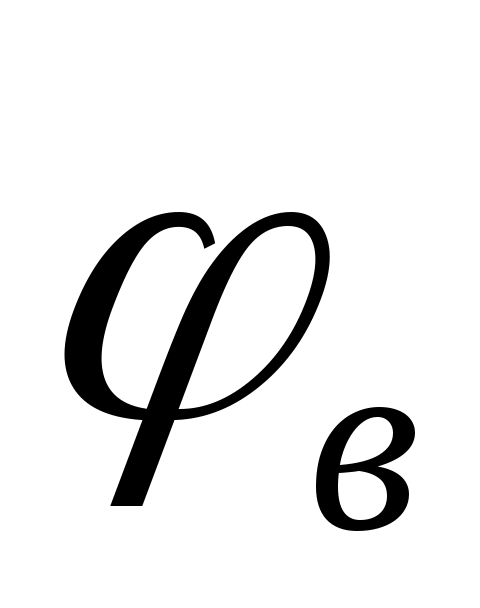 - угол возврата (опускания);
- угол возврата (опускания); 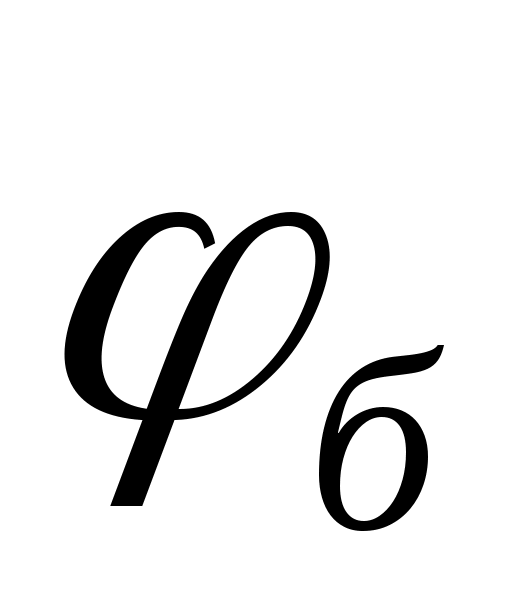 - угол ближнего выстоя.
- угол ближнего выстоя.
С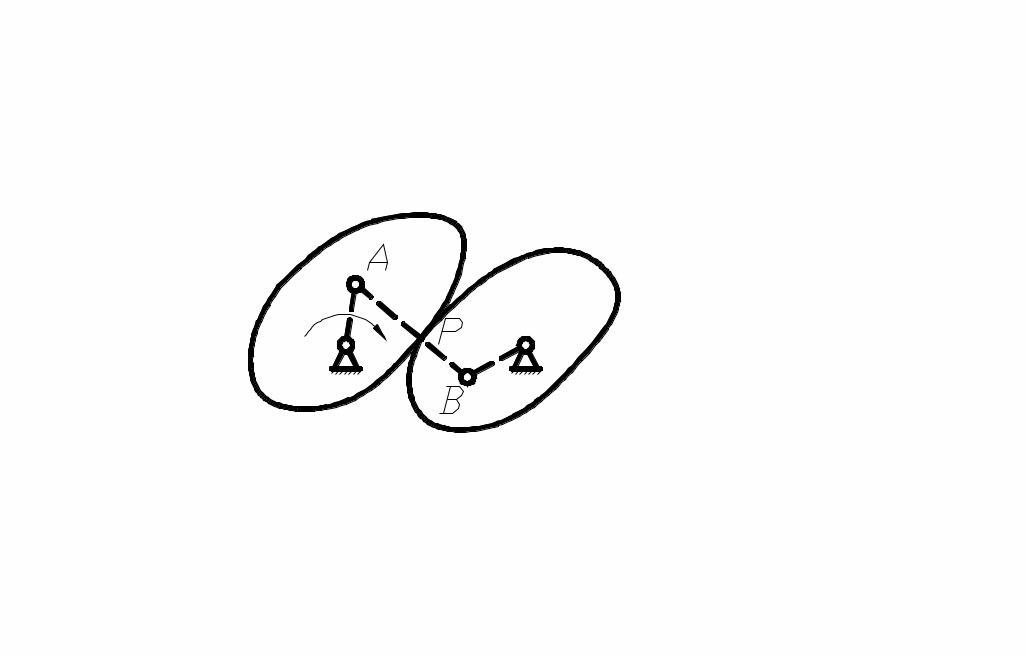 целью непосредственного определения скоростей и ускорений толкателя осуществляют условную замену высшей пары на низшую. Замена осуществляется так, что движение заменяемого механизма в момент замены соответствует движению заменяющего.
целью непосредственного определения скоростей и ускорений толкателя осуществляют условную замену высшей пары на низшую. Замена осуществляется так, что движение заменяемого механизма в момент замены соответствует движению заменяющего.
В общем случае мгновенный заменяющий механизм представляет шарнирный четырёхзвенник с подвижными шарнирами А и В, расположенными в центрах кривизны, контактирующих в точке Р профилей (рис. 49).
В частных случаях возможны различные
рис.49 варианты замены (рис 50), при этом можно производить кинематический анализ кулачкового механизма как обычного стержневого.
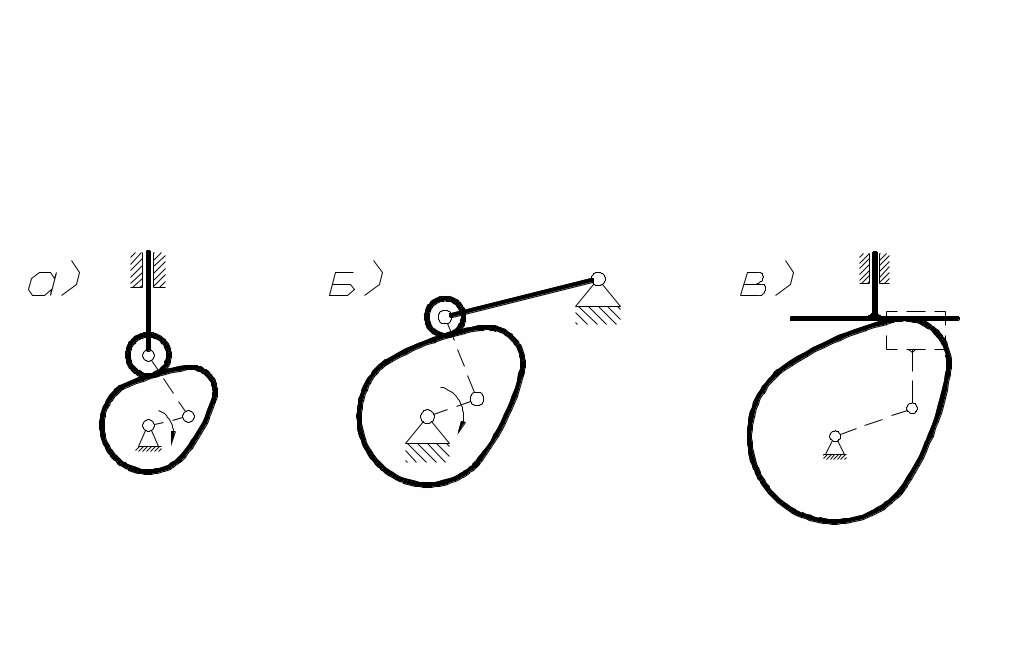
рис. 50
∆
πkв,
получим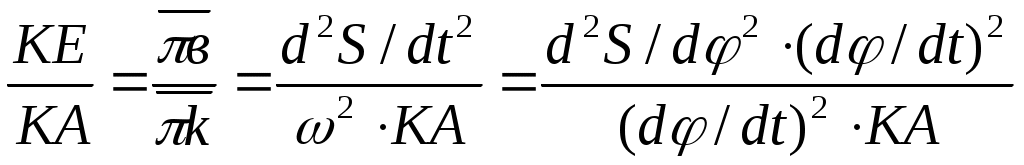 ,
,
т. е.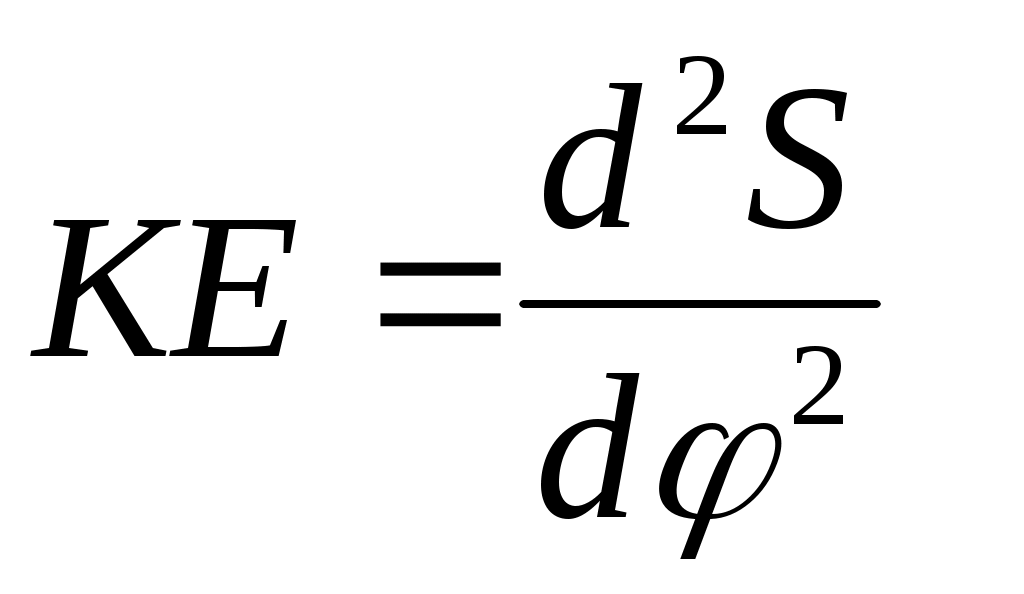 и
и 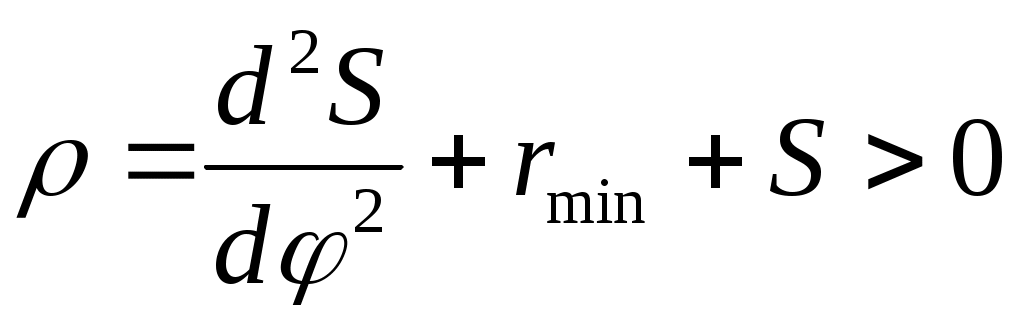 или
или
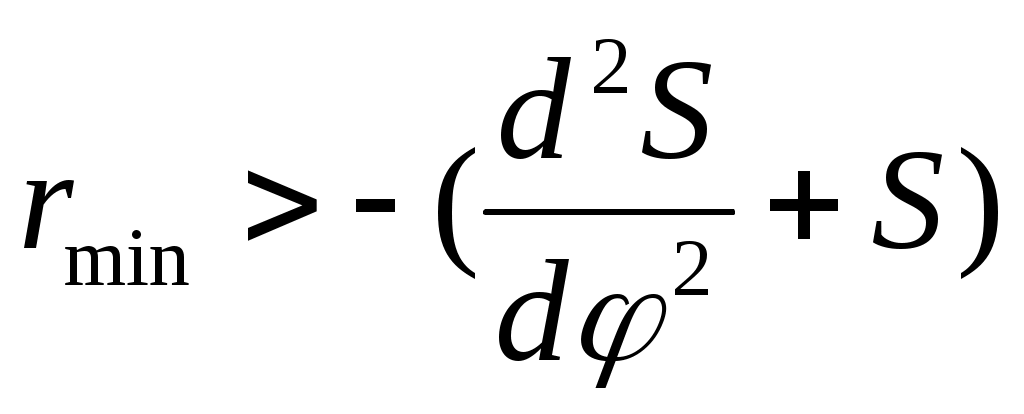 .
.
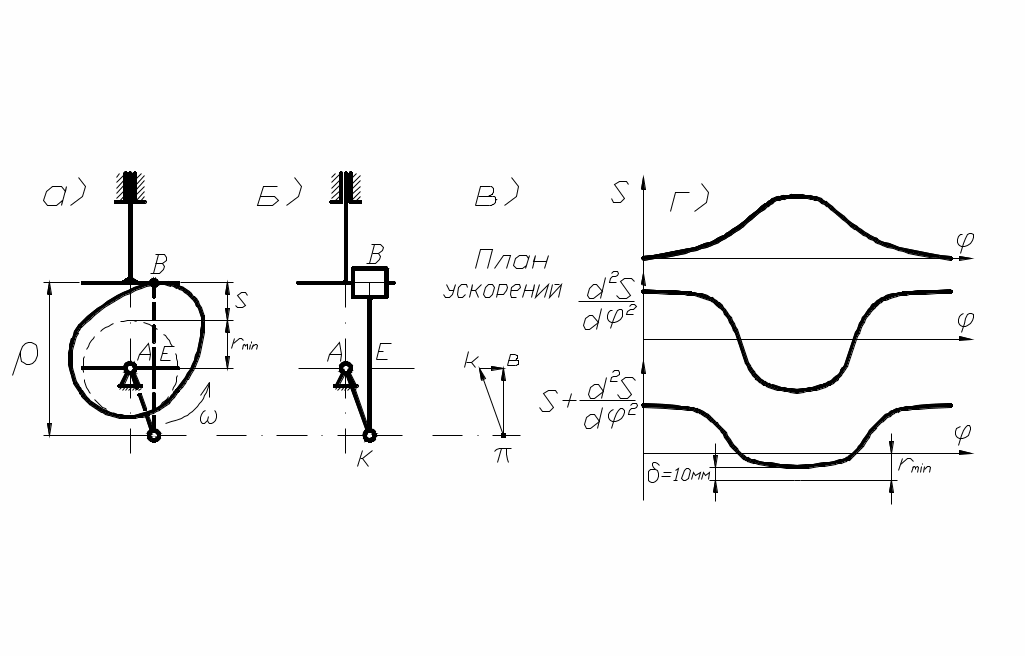
рис. 60
Следовательно, просуммировав две диаграммы S(φ) и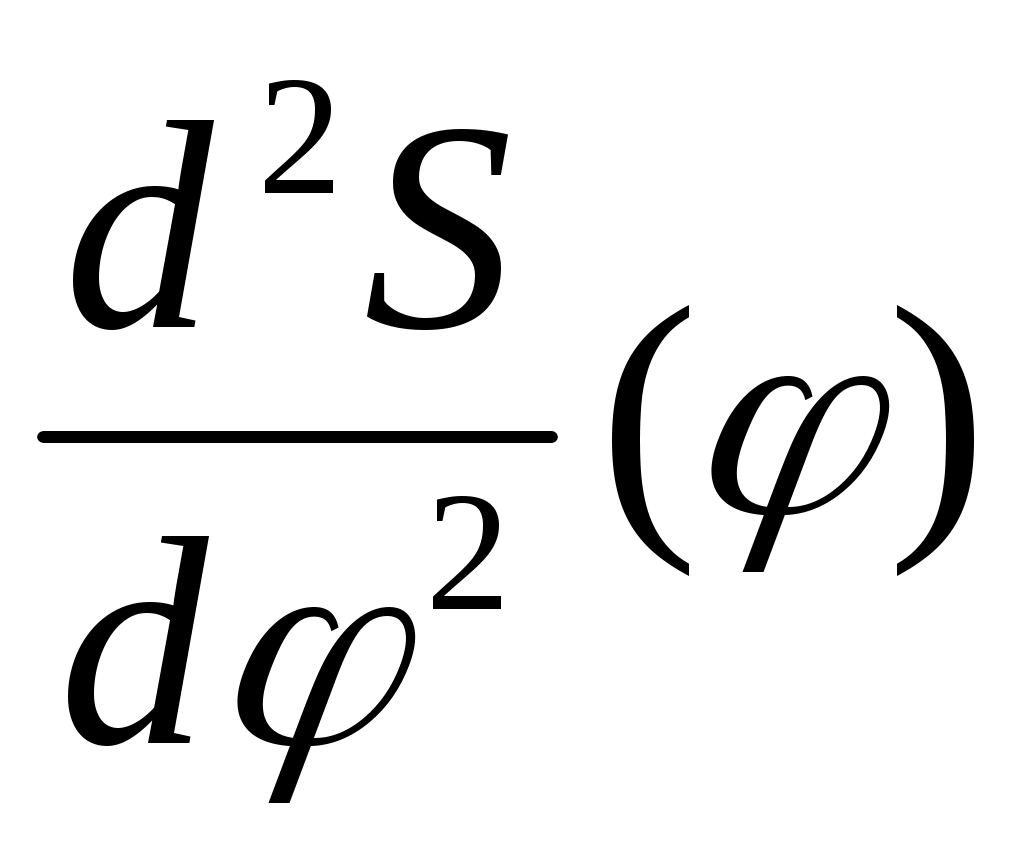 , построенные в одном масштабе
, построенные в одном масштабе 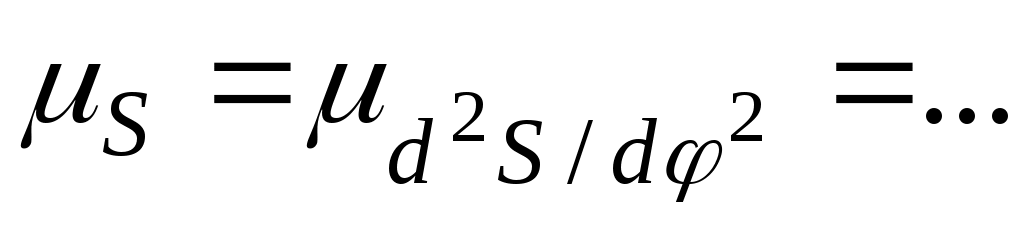 , получим величину rmin (рис. 61, г) имеющую несколько большее значение, чем абсолютная величина отрицательной ординаты на суммарной диаграмме.
, получим величину rmin (рис. 61, г) имеющую несколько большее значение, чем абсолютная величина отрицательной ординаты на суммарной диаграмме.
8. Фрикционные и зубчатые механизмы
Фрикционные и зубчатые механизмы предназначены для передачи вращательного движения с одного вала на другой с помощью деталей типа диска в основном цилиндрической формы. При этом, как правило, меняется величина угловой скорости и передаваемого момента, а также их направление. Вал, от которого передаётся движение, называется ведущим, а вал, которому передаётся движение – ведомым.
Оси валов могут быть параллельными, пересекаться или перекрещиваться под различными углами. В первом случае механизм является плоским, в остальных случаях механизмы пространственные.
8.1. Общие сведения о передачах вращения
Если в механизме имеются только ведущие и ведомые валы и отсутствуют промежуточные вращающиеся звенья, то механизм называется передачей. Передача вращения может осуществляться:
1) путём непосредственного соприкосновения двух дисков, жёстко связанных с ведущим и ведомым валами (фрикционная, червячная, зубчатая);
2) посредством промежуточных гибких тел, сцепляющихся с дисками, которые жёстко связаны с ведущим и ведомым валами (ременная, цепная, волновая).
Отношения угловых скоростей вращения обоих валов передачи называется передаточным отношением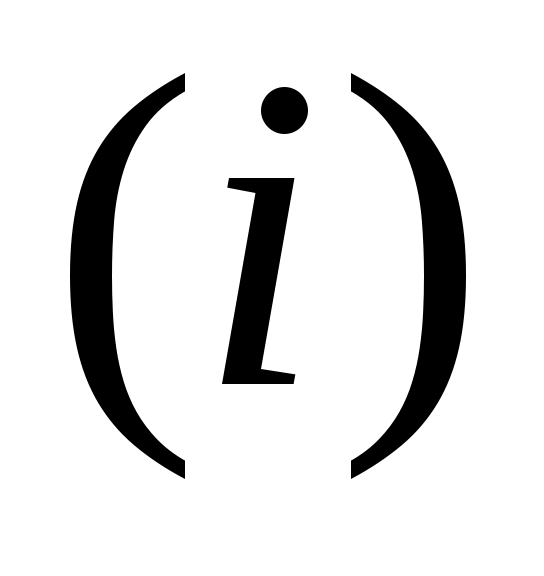 , которое характеризует процесс преобразования движения количественно.
, которое характеризует процесс преобразования движения количественно.
Отношения угловой скорости ведущего вала к угловой скорости ведомого называется
передаточным числом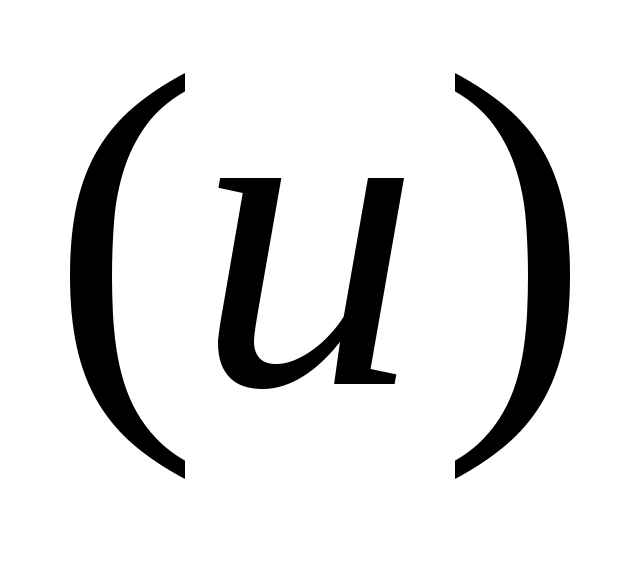 , которое определяет направление передачи энергии.
, которое определяет направление передачи энергии.
Величина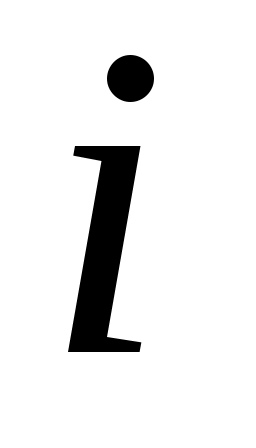 и
и 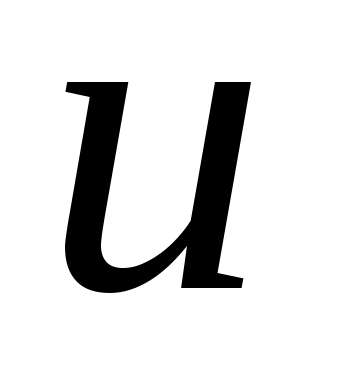 может меняться или оставаться постоянным за время одного оборота ведущего вала.
может меняться или оставаться постоянным за время одного оборота ведущего вала.
Любую передачу можно схематично представить в виде двух начальных поверхностей, контактирующих между собой, а плоскую передачу – в виде двух начальных окружностей, перекатывающихся друг по другу без скольжения и контактирующих в полюсе р (рис. 61). Тогда
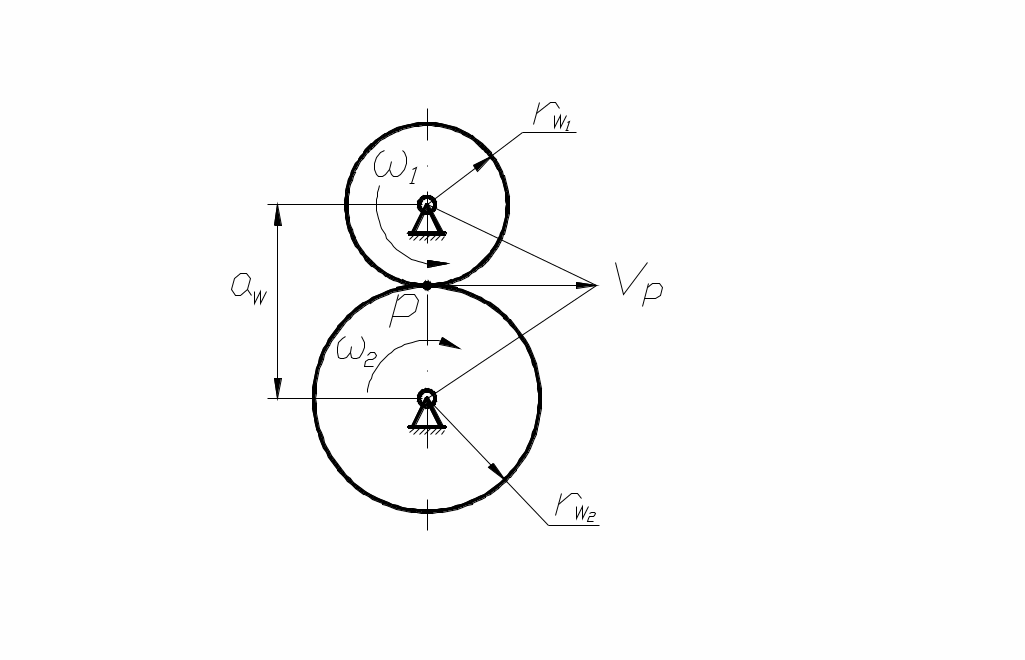
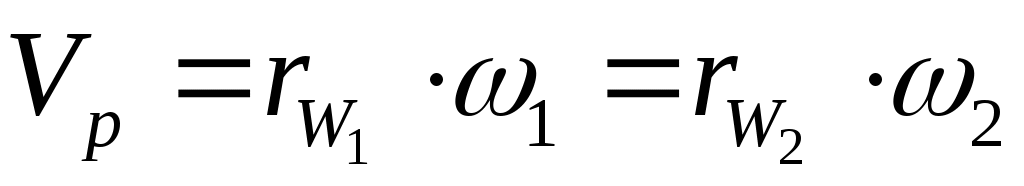 , т. е.
, т. е.
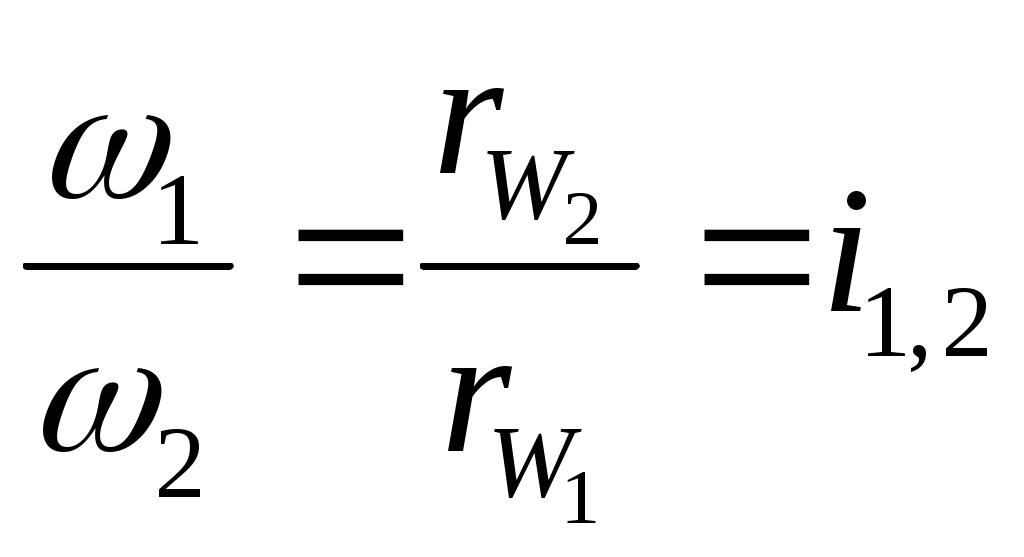 - передаточное число.
- передаточное число.
рис. 61
Аналогично можно изобразить ременную или цепную передачи, а также пространственные передачи (рис. 62).
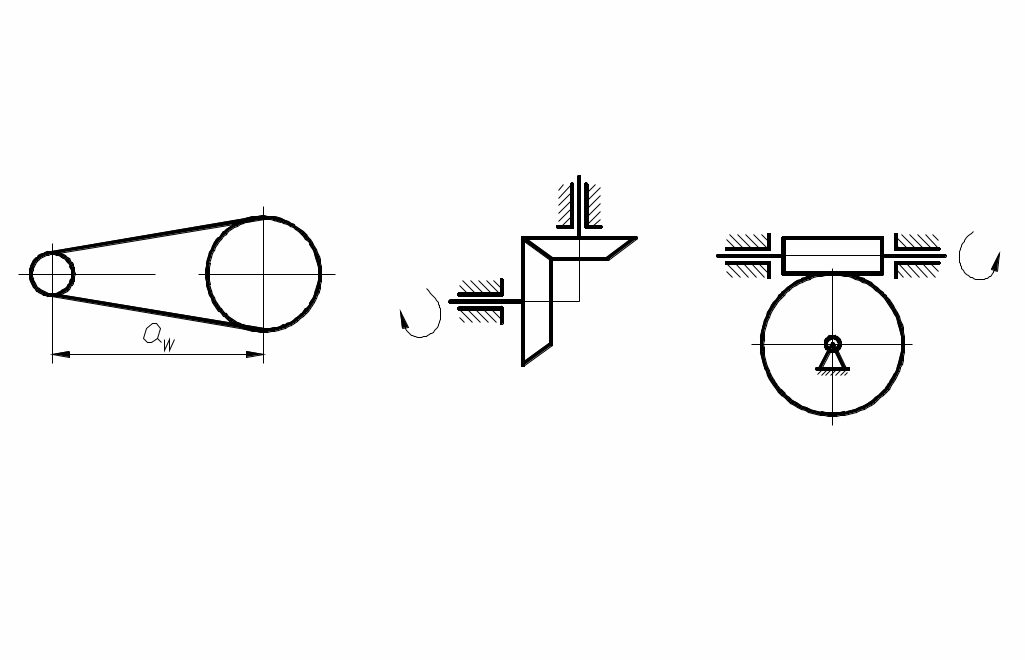
рис. 62
8.2. Фрикционные передачи
О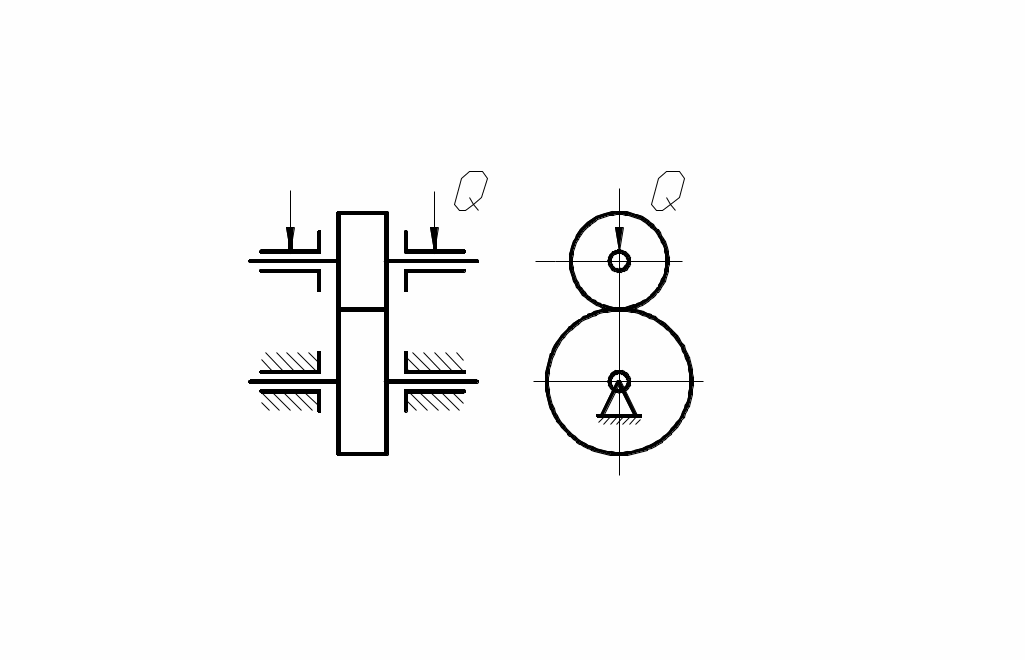 дной из наиболее простых и во многих случаях достаточно надёжной является фрикционная передача, состоящая в простейшем случае из двух колёс (катков), закреплённых на ведущем и ведомом валах. Для передачи движения без скольжения необходимо приложить к одному из колёс силу Q, достаточную для возникновения трения в месте контакта (рис. 63), при этом касательная сила их сцепления равна по величине передаваемого окружному усилию.
дной из наиболее простых и во многих случаях достаточно надёжной является фрикционная передача, состоящая в простейшем случае из двух колёс (катков), закреплённых на ведущем и ведомом валах. Для передачи движения без скольжения необходимо приложить к одному из колёс силу Q, достаточную для возникновения трения в месте контакта (рис. 63), при этом касательная сила их сцепления равна по величине передаваемого окружному усилию.
рис. 63
Фрикционные передачи могут быть с постоянным и переменным передаточным отношением. Последние называются вариаторами (рис. 64 а, б).
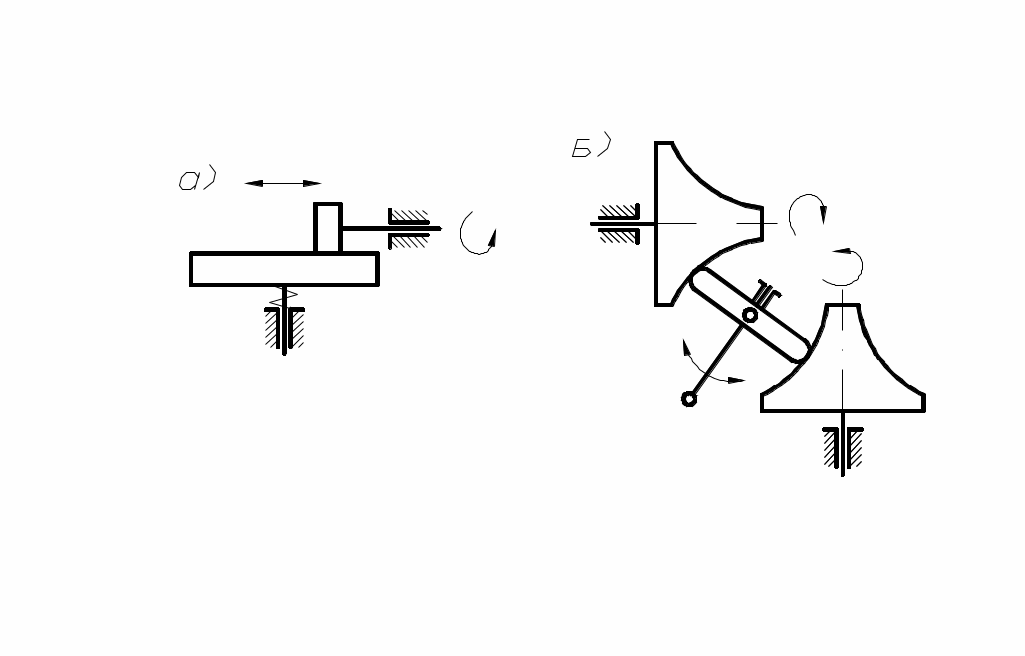
рис. 64
Достоинствами фрикционных передач являются: плавность и бесшумность в работе, простота конструкции, невозможность поломки при резком изменении крутящего момента на одном из валов благодаря возможности проскальзывания катков, возможность бесступенчатого регулирования скоростей.
Недостатками являются: необходимость прижимного устройства, непостоянство передаточного отношения, невозможность передачи значительных крутящих моментов.
В связи с указанными недостатками фрикционные передачи не получили такого широкого распространения как зубчатые.
цирования графиков
Движение толкателя имеет реверсивный характер за весь кинематический цикл, при этом наблюдаются 4 фазы движения толкателя, соответствующие 4 фазовым углам поворота кулачка:
С
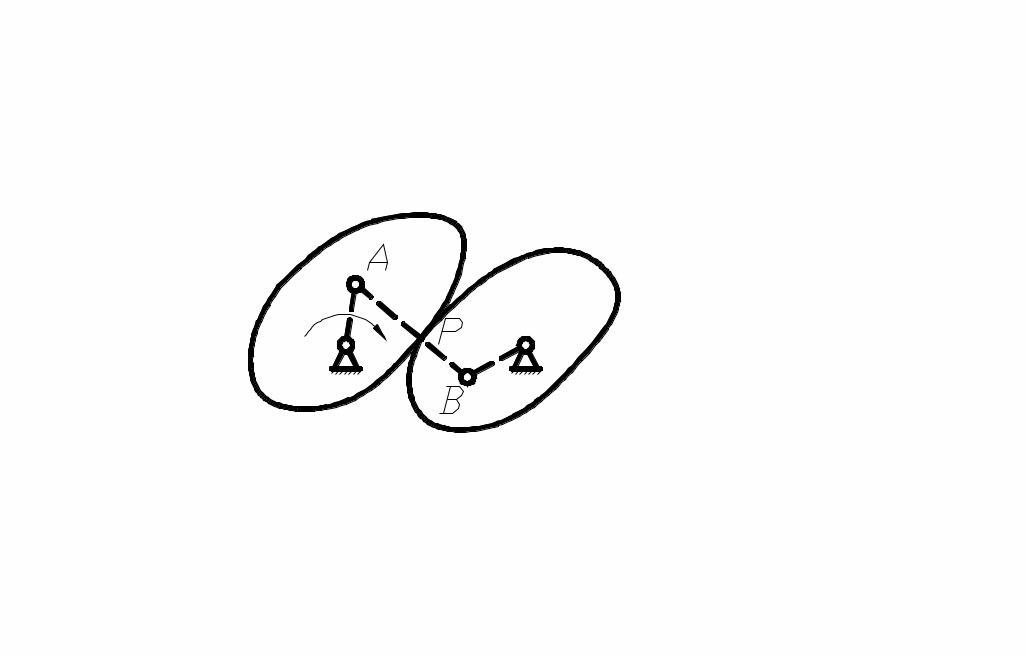 целью непосредственного определения скоростей и ускорений толкателя осуществляют условную замену высшей пары на низшую. Замена осуществляется так, что движение заменяемого механизма в момент замены соответствует движению заменяющего.
целью непосредственного определения скоростей и ускорений толкателя осуществляют условную замену высшей пары на низшую. Замена осуществляется так, что движение заменяемого механизма в момент замены соответствует движению заменяющего.В общем случае мгновенный заменяющий механизм представляет шарнирный четырёхзвенник с подвижными шарнирами А и В, расположенными в центрах кривизны, контактирующих в точке Р профилей (рис. 49).
В частных случаях возможны различные
рис.49 варианты замены (рис 50), при этом можно производить кинематический анализ кулачкового механизма как обычного стержневого.
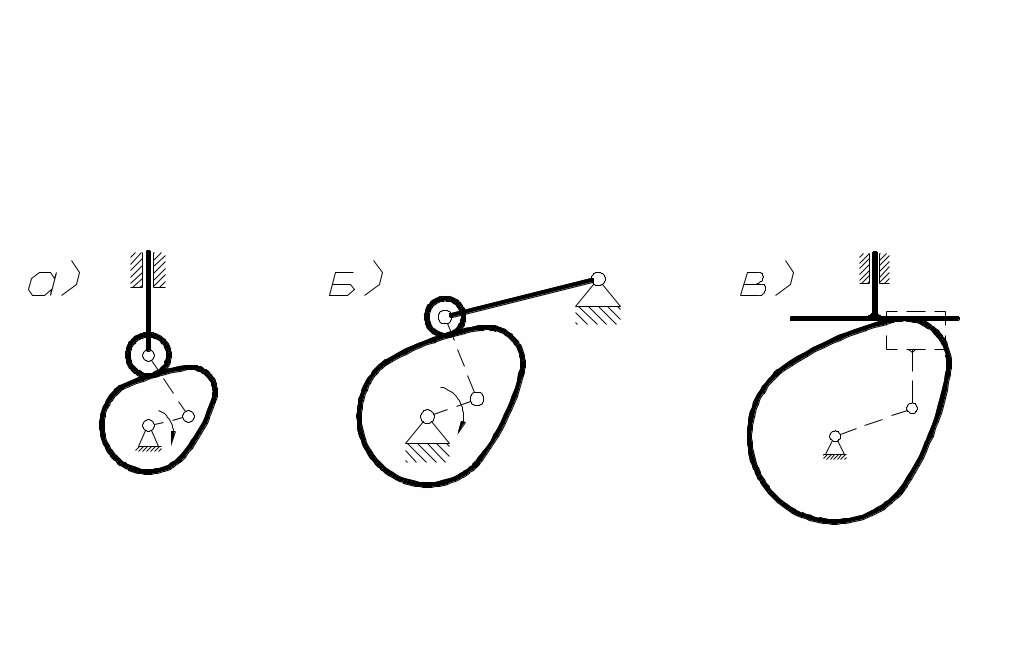
рис. 50
7.3. Некоторые вопросы динамического анализа кулачковых механизмов
Условия нормальной работы звеньев кулачкового механизма в существенной степени зависит от угла давления  между вектором усилия F, действующего на толкатель со стороны кулачка, и вектором скорости V толкателя (рис.51,а).
между вектором усилия F, действующего на толкатель со стороны кулачка, и вектором скорости V толкателя (рис.51,а).
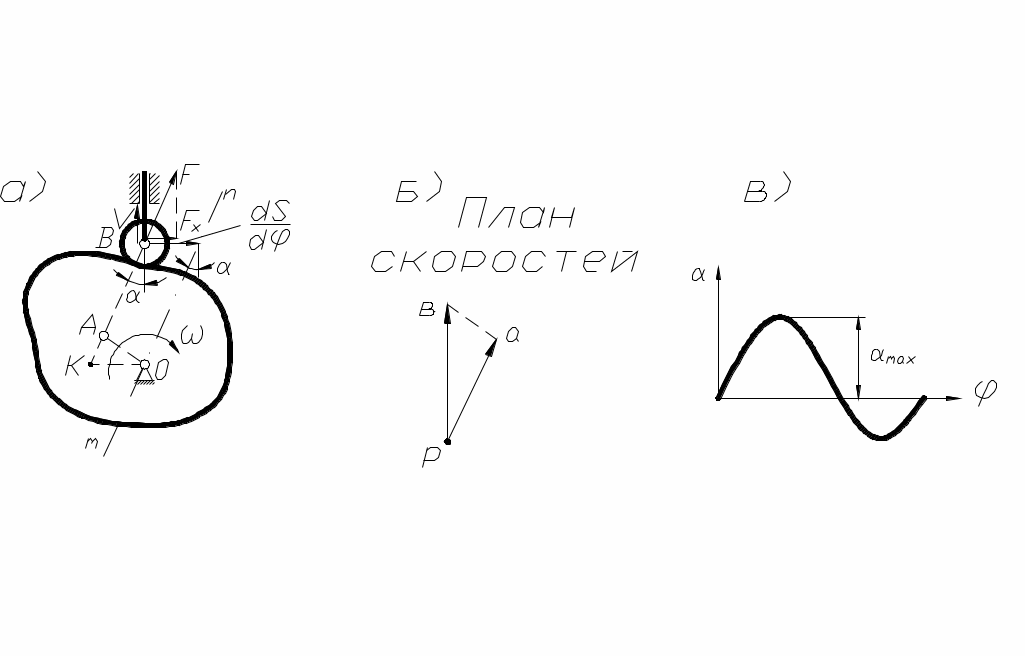
рис. 51
Угол давления – переменная величина, с увеличением которой возрастает опасность заклинивания механизма, т. к. увеличивается составляющая 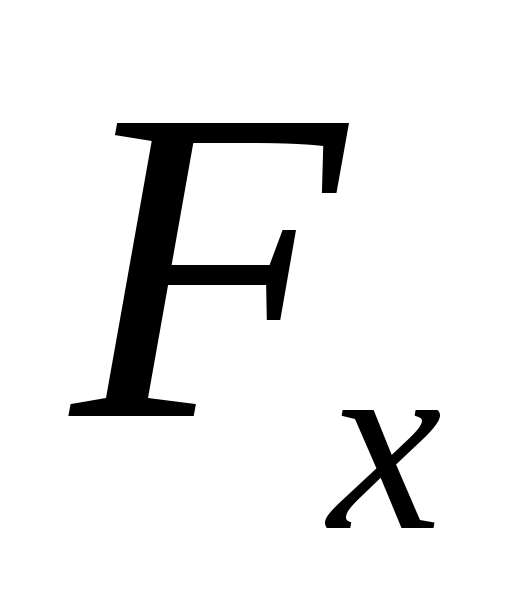 , вызывающая трение в кинематических парах (рис. 51).
, вызывающая трение в кинематических парах (рис. 51).
Обычно величину 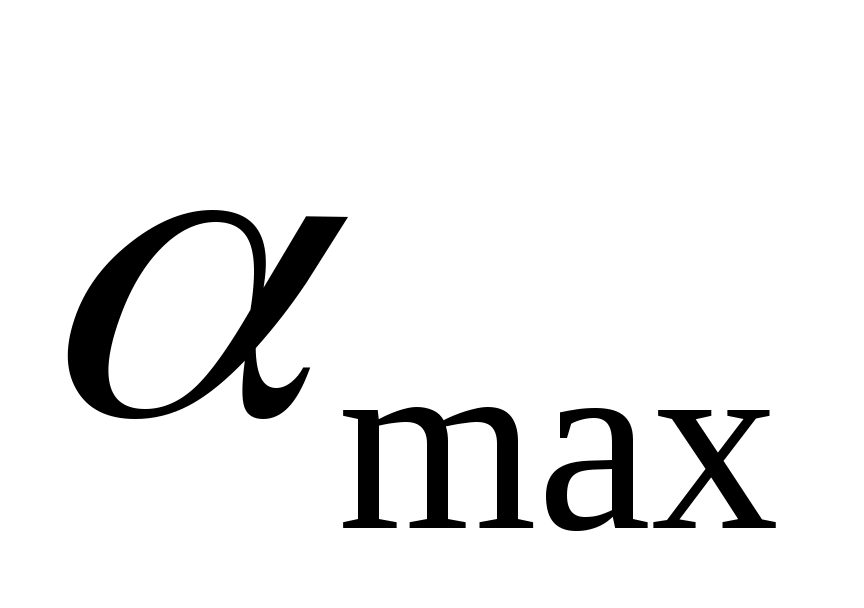 ограничивают подбором размеров кулачка при условии что:
ограничивают подбором размеров кулачка при условии что:
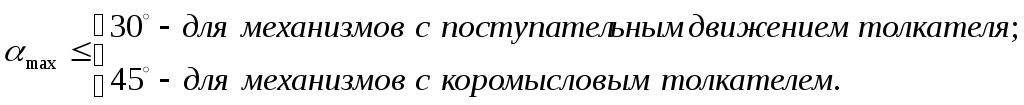
Рассмотрим задачу определения текущего угла  для любого положения механизма. Построим заменяющий кривошипно-ползунный механизм ОАВ, где точка А совпадает с центром кривизны кулачка в точке его контакта с роликом.
для любого положения механизма. Построим заменяющий кривошипно-ползунный механизм ОАВ, где точка А совпадает с центром кривизны кулачка в точке его контакта с роликом.
Рассмотрим план скоростей заменяющего механизма (рис. 51, б), где:
 ∆рав
∆рав
∆ОАК (∆ с взаимноперепендикулярными сторонами), т. е.
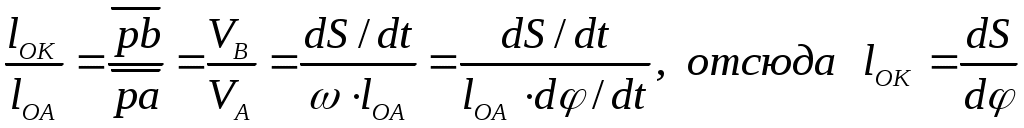 .
.
Т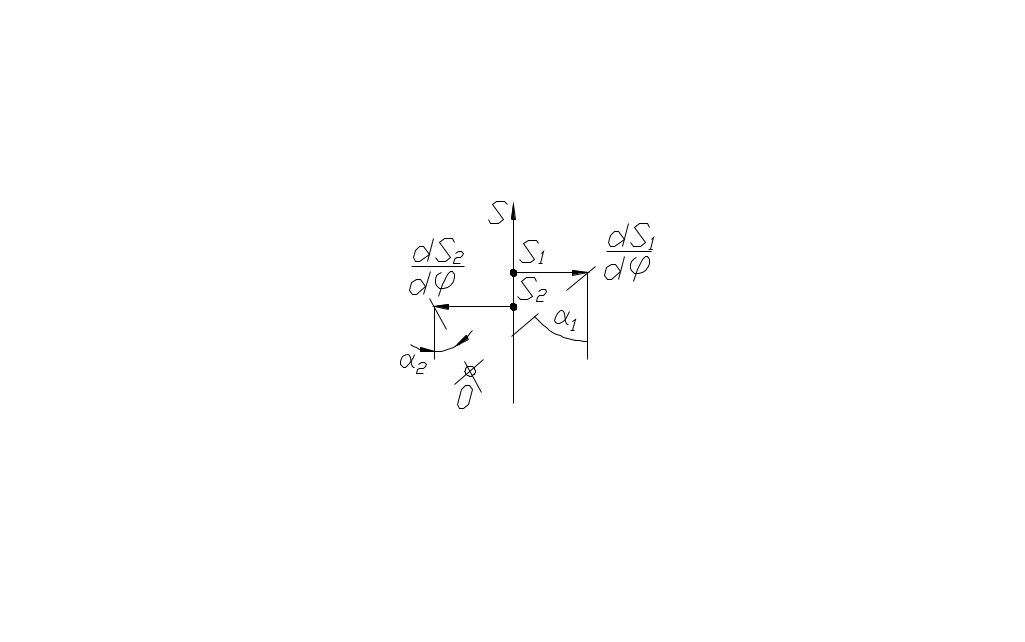 аким образом, отложив вектор dS/dφ от точки В в направлении вектора скорости V толкателя, повёрнутого на 90º в сторону вращения кулачка и проведя линию mn через точку О и конец вектора dS/dφ, получим угол
аким образом, отложив вектор dS/dφ от точки В в направлении вектора скорости V толкателя, повёрнутого на 90º в сторону вращения кулачка и проведя линию mn через точку О и конец вектора dS/dφ, получим угол  (рис. 51).
(рис. 51).
Можно решить обратную задачу, находя положение центра “О” вращения кулачка при заданных значениях  и dS/dφ для двух положений толка-
и dS/dφ для двух положений толка-
рис. 52 теля (рис. 52).
Из рис. 52 видно, что чем больших значений достигают углы давления  , тем меньшие габариты имеет механизм, но риск заклинивания при этом увеличивается.
, тем меньшие габариты имеет механизм, но риск заклинивания при этом увеличивается.
7.4. Синтез кулачковых механизмов
При проектировании кулачковых механизмов используются различные методы синтеза.
Если известен минимальный радиус (rmin) кулачка и закон его движения, то построение профиля – задача кинематического синтеза. Если rmin должен определяться с условием отсутствия заклинивания, то построение профиля – задача динамического синтеза.
7.4.1. Выбор закона движения толкателя
В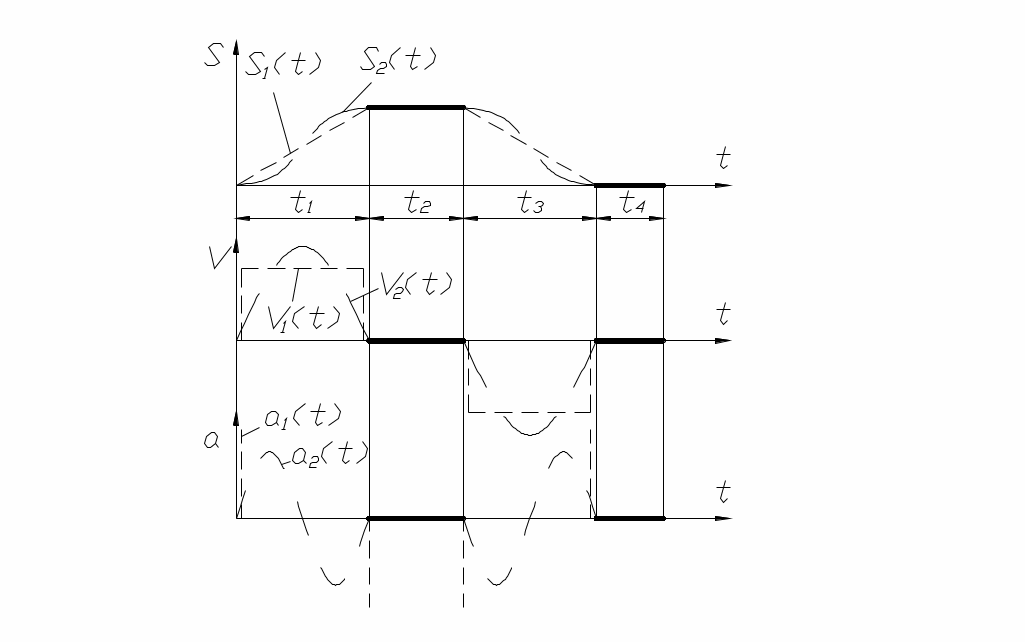 опрос о выборе закона движения толкателя отпадает в случае, если он полностью определяется той операцией, которую толкатель осуществляет, т. е. задан. Однако во многих случаях заданы лишь частичные перемещения, скорости или ускорения толкателя и необходимо подобрать какой-либо закон движения на недостающих участках.
опрос о выборе закона движения толкателя отпадает в случае, если он полностью определяется той операцией, которую толкатель осуществляет, т. е. задан. Однако во многих случаях заданы лишь частичные перемещения, скорости или ускорения толкателя и необходимо подобрать какой-либо закон движения на недостающих участках.
Например, может быть задано максимальное и минимальное перемещение толкателя по двум участкам t2 и t4 (рис. 53) в виде графика S(t), показанного основной линией. На остальных участках t1 и t3 закон движения следует выбрать.
Из всех возможных законов движения необходимо выбирать оптимальный с точки зрения усло-
вий работы механизма. Одним из таких законов является синусоидальный закон S2(t), обеспечи-
рис. 53 вающий плавную безударную работу механизма без резких изменений скорости и без больших значений ускорений, как, например, при выборе закона S1(t), где ускорения, а следовательно силы инерции достигают больших величин, способных вызвать износ и поломку.
7.4.2. Профилирование кулачка
Рассмотрим графический метод получения профиля кулачка как задачу кинематического синтеза. В этом случае заданы схема кулачкового механизма, закон движения толкателя и rmin кулачка. Профилирование осуществляется на основе закона движения толкателя. В качестве примера рассмотрим профилирование кулачка в осевом механизме с поступательно движущимся толкателем. При этом дана схема механизма, диаграмма движения толкателя и rmin кулачка (рис. 54).
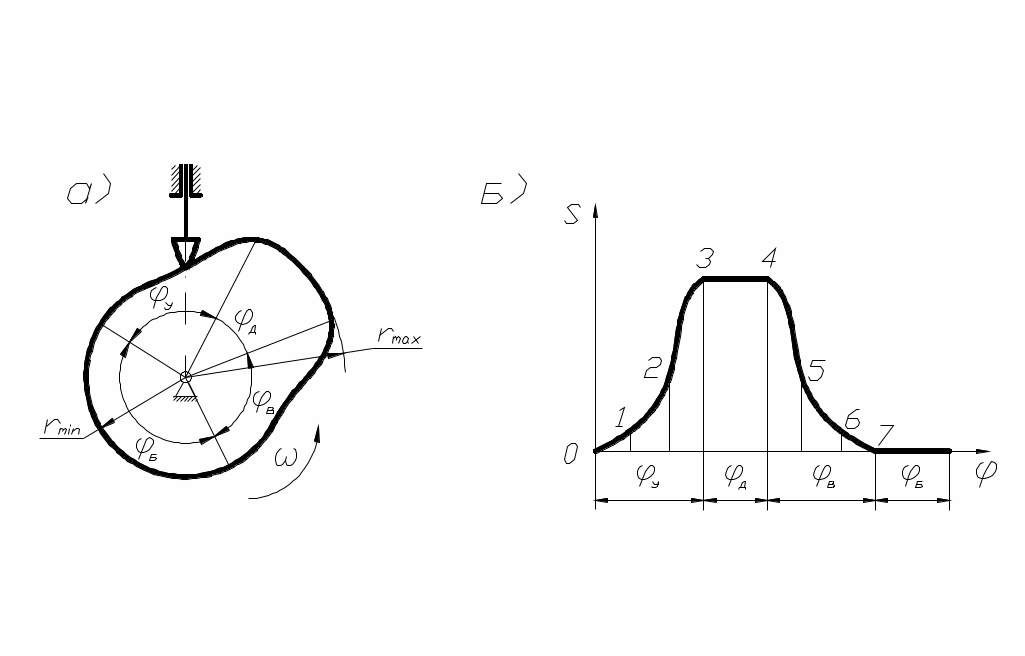
рис. 54
В начале размечаются основные размеры механизма в масштабе 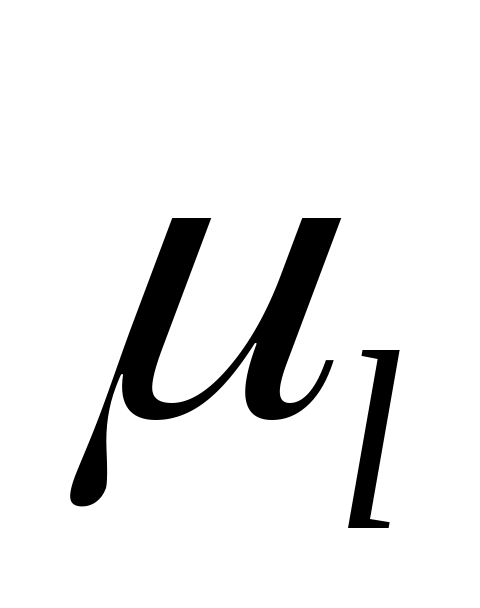 , а также фазовые углы, причём углы
, а также фазовые углы, причём углы 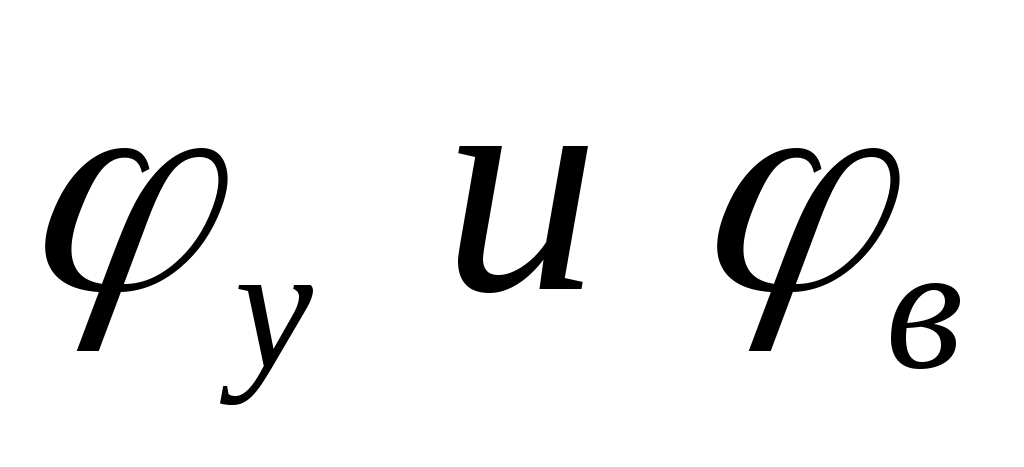 делятся на ряд равных частей в соответствии с диаграммой (рис. 54, б). Строятся начальное, а затем ряд последующих положений толкателя в обращённом движении (рис. 55, а), и полученные точки соединяются плавной кривой. В случае построения профиля кулачка для механизма с роликовым толкателем сначала строится эквидистанта (центровой профиль) как и в предыдущем случае, а затем и сам рабочий профиль кулачка, отстоящий от эквидистанты на величину радиуса ролика rрол (рис. 55, б).
делятся на ряд равных частей в соответствии с диаграммой (рис. 54, б). Строятся начальное, а затем ряд последующих положений толкателя в обращённом движении (рис. 55, а), и полученные точки соединяются плавной кривой. В случае построения профиля кулачка для механизма с роликовым толкателем сначала строится эквидистанта (центровой профиль) как и в предыдущем случае, а затем и сам рабочий профиль кулачка, отстоящий от эквидистанты на величину радиуса ролика rрол (рис. 55, б).
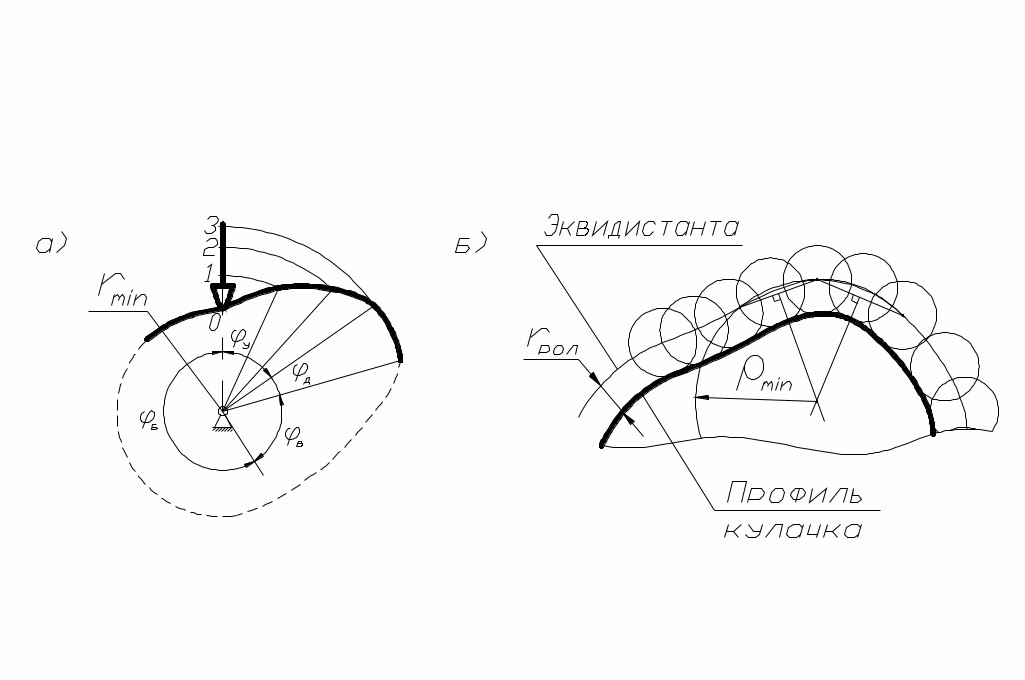
рис. 55
Величина rрол выбирается из соотношения: 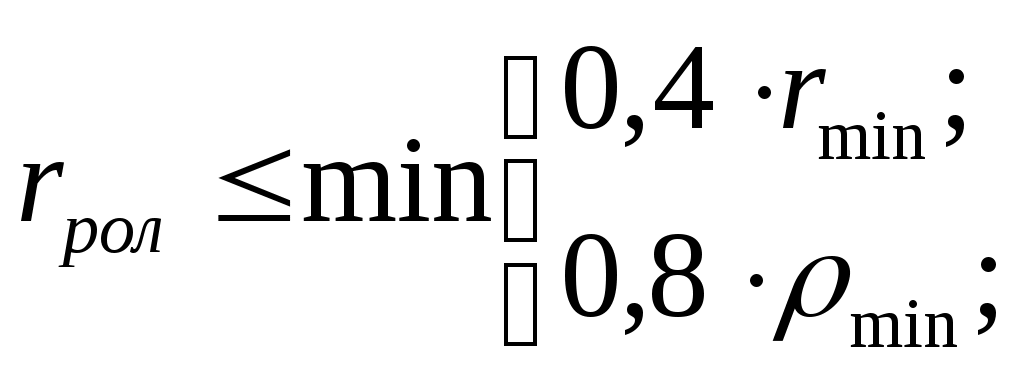
где ρmin – минимальный радиус центрового профиля кулачка, который можно определить графически по трём точкам в месте наибольшей кривизны эквидистанты (рис. 55, б).
Профилирование кулачка механизма с коромысловым толкателем состоит из аналогичных операций, т. е. после разметки межцетровых расстояний строится ряд положений коромысла в обращённом движении (рис. 56) в соответствии с заданной диаграммой S(φ), часть которой показана на рис. 56, б.
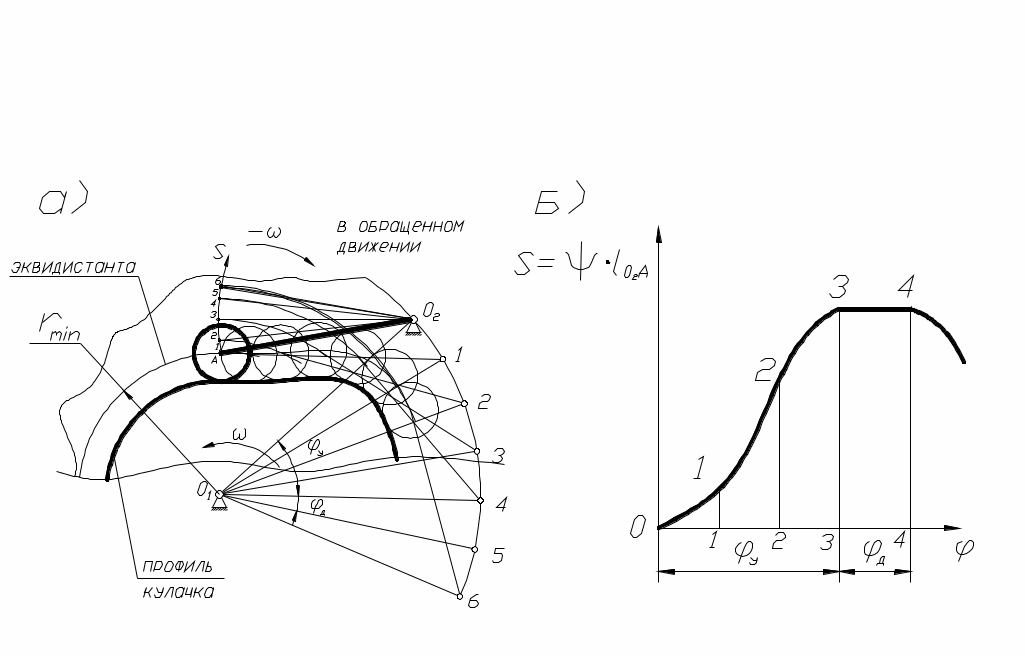
рис. 56
7.4.3. Динамический синтез кулачкового механизма
Задача динамического синтеза заключается в нахождении центра вращения кулачка, при условии минимизации размеров механизма, когда заданы: закон движения толкателя и предельно допустимый угол давления 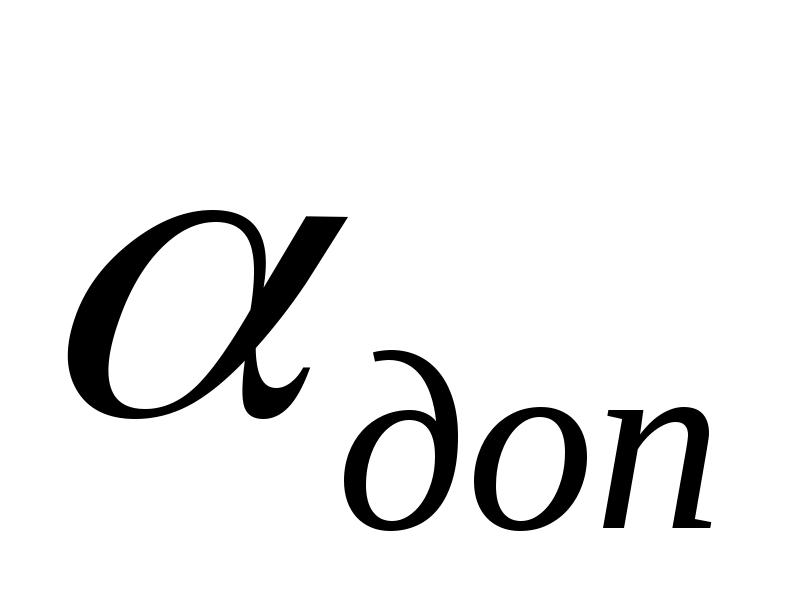 . В конечном итоге задача состоит в определении rmin кулачка, после чего может быть решена задача кинематического синтеза (профилирование).
. В конечном итоге задача состоит в определении rmin кулачка, после чего может быть решена задача кинематического синтеза (профилирование).
Рассмотрим пример определения rmin кулачка для механизма с поступательно движущимся толкателем, когда заданы диаграммы перемещений S(φ) и аналогов скоростей dS/dφ(φ), которые должны быть вычерчены в едином масштабе 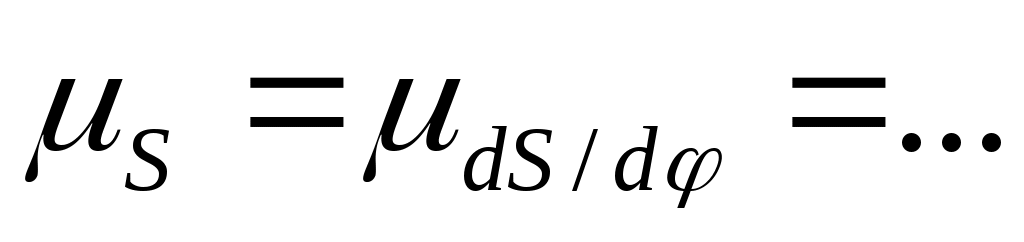
Путём исключения параметра φ вычерчивается совмещённая диаграмма S(dS/dφ), как показано на рис. 57.
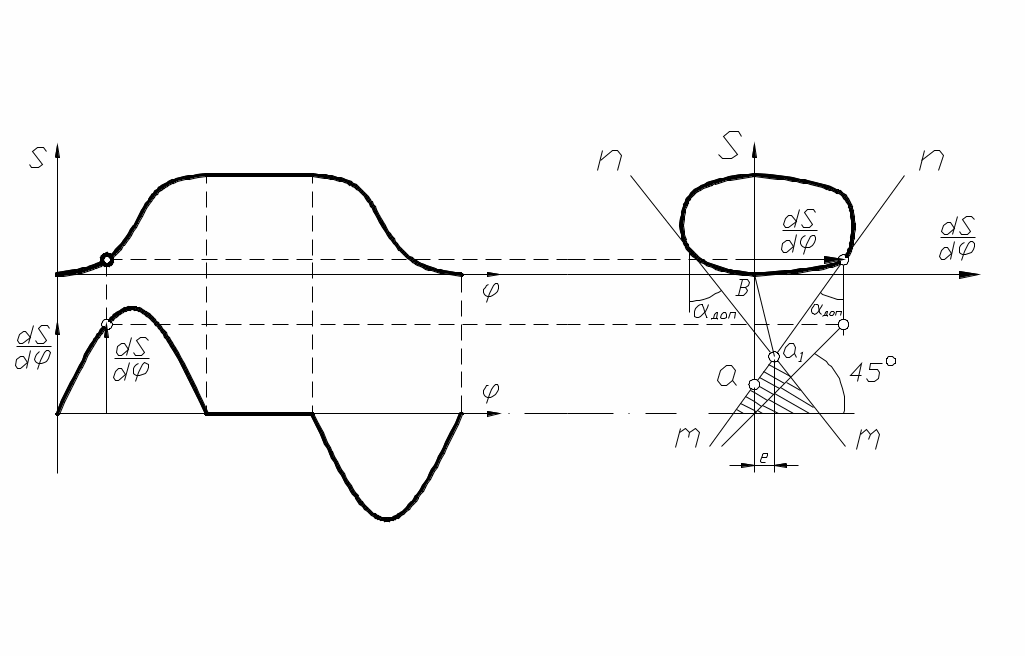
рис. 57
Проведя касательные mn к диаграмме S(dS/dφ) под углами 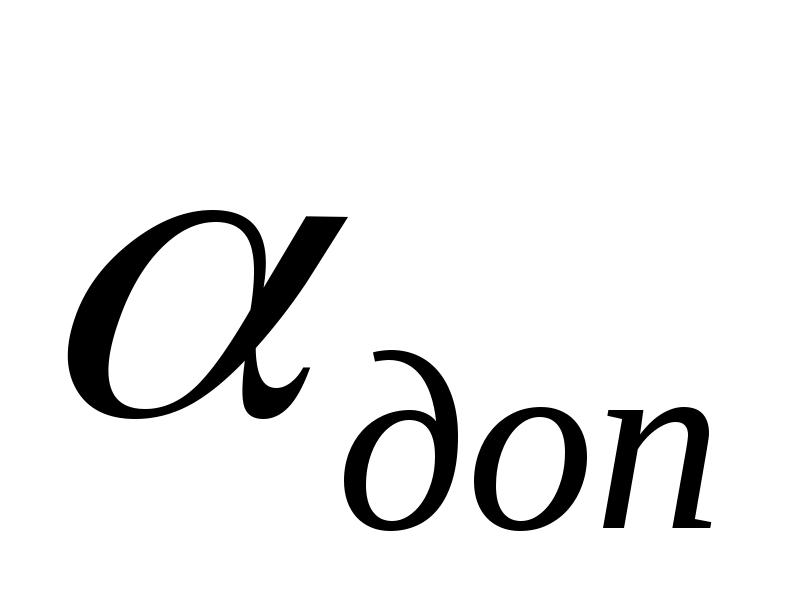 , как показано на рис. 57, получим точку
, как показано на рис. 57, получим точку 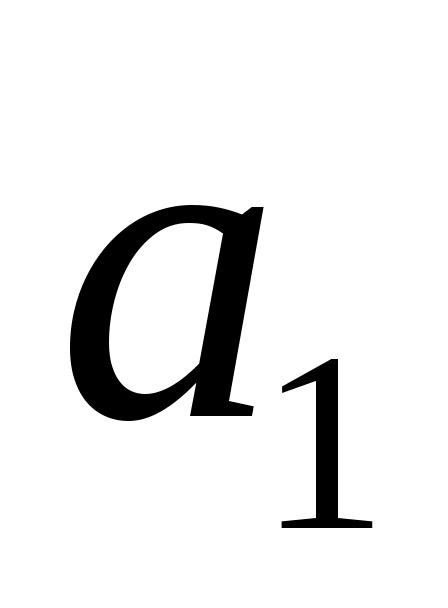 на их пересечении. Тогда отрезок
на их пересечении. Тогда отрезок 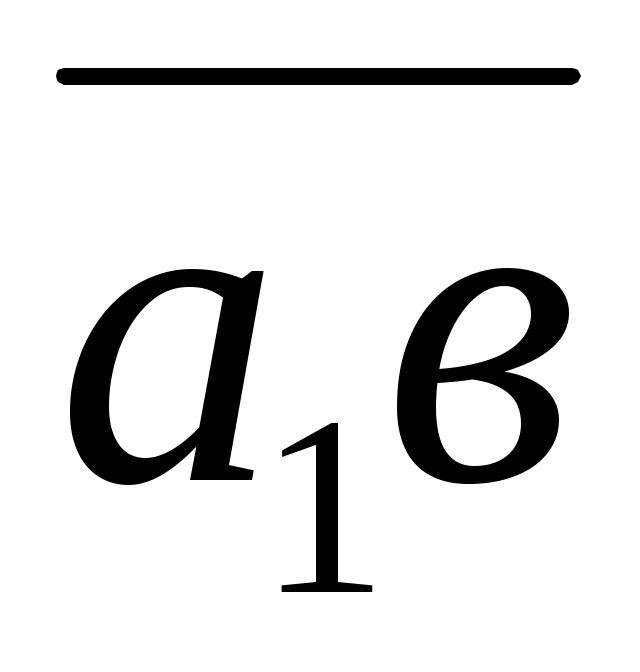 будет соответствовать в масштабе
будет соответствовать в масштабе 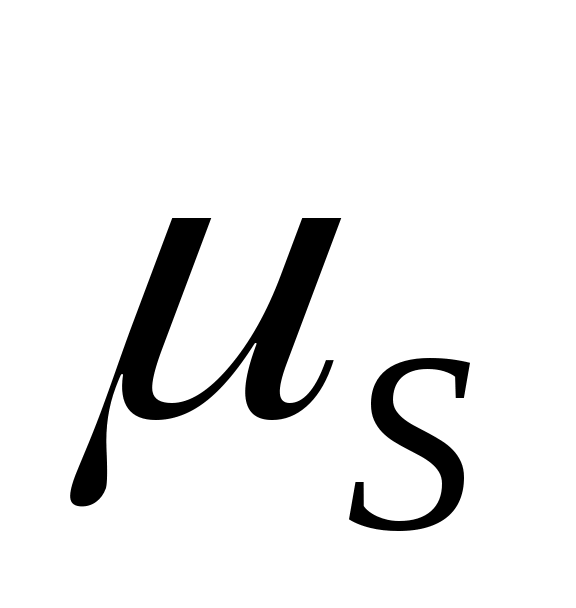 величине
величине 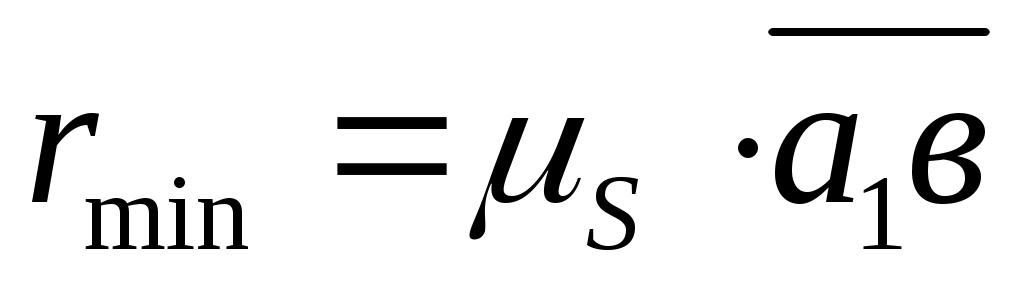 для внеосного механизма со смещением оси толкателя е≠0 относительно центра вращения кулачка. Так как центр кулачка можно располагать в любой точке заштрихованной области, то при е=0 получим
для внеосного механизма со смещением оси толкателя е≠0 относительно центра вращения кулачка. Так как центр кулачка можно располагать в любой точке заштрихованной области, то при е=0 получим 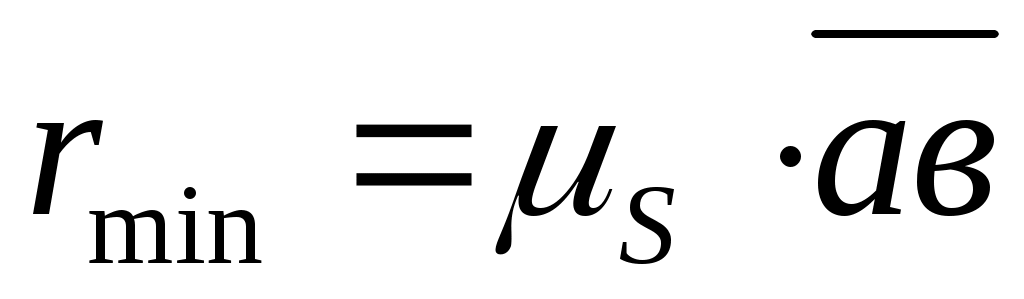 , когда центр кулачка совпадает с осью толкателя. Таким образом, габариты механизма уменьшаются при е≠0, т. к. центр кулачка приближается к точке в, а предельный угол давления
, когда центр кулачка совпадает с осью толкателя. Таким образом, габариты механизма уменьшаются при е≠0, т. к. центр кулачка приближается к точке в, а предельный угол давления 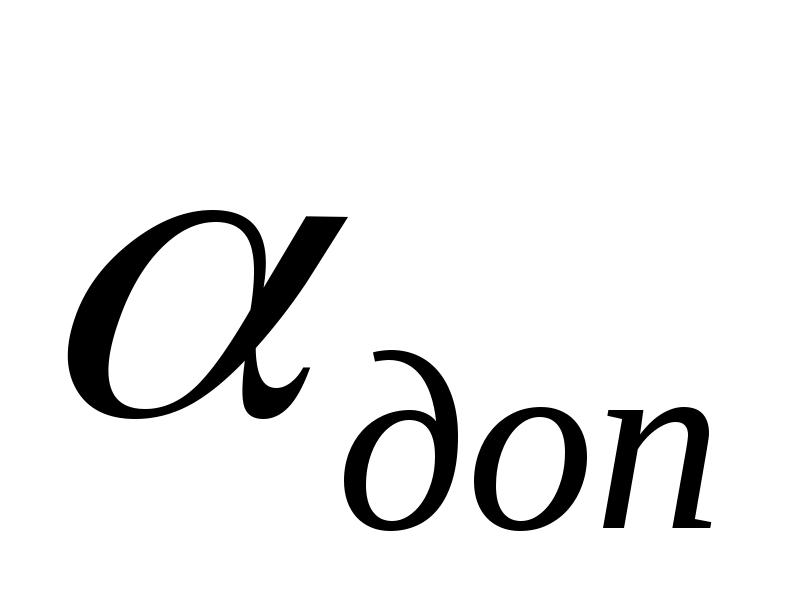 остаётся неизменным.
остаётся неизменным.
Обычно при силовом замыкании такие построения делаются только для фазы удаления, т. к. на фазе возврата толкатель является ведущим звеном и заклинивания не происходит.
Для механизма с коромысловым толкателем построение совмещённой диаграммы S(dS/dφ) производится в пределах заданного максимального угла размаха коромысла Ψmax. Причём отрезки, равные dS/dφ откладываются в масштабе 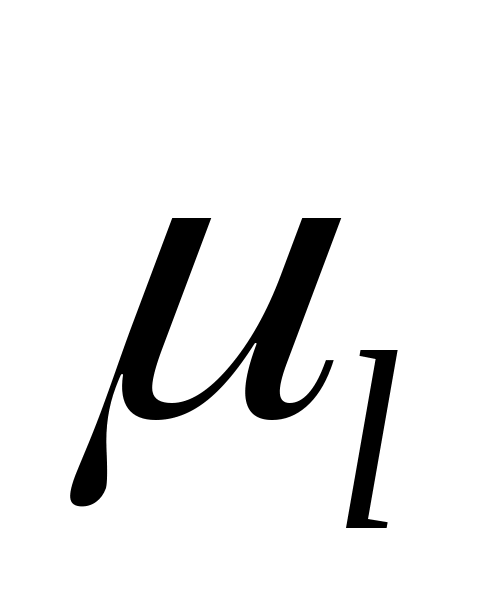 от траектории точки А коромысла по его оси в сторону вектора dS/dφ, повёрнутого на 90º в направлении вращения кулачка (рис. 58).
от траектории точки А коромысла по его оси в сторону вектора dS/dφ, повёрнутого на 90º в направлении вращения кулачка (рис. 58).
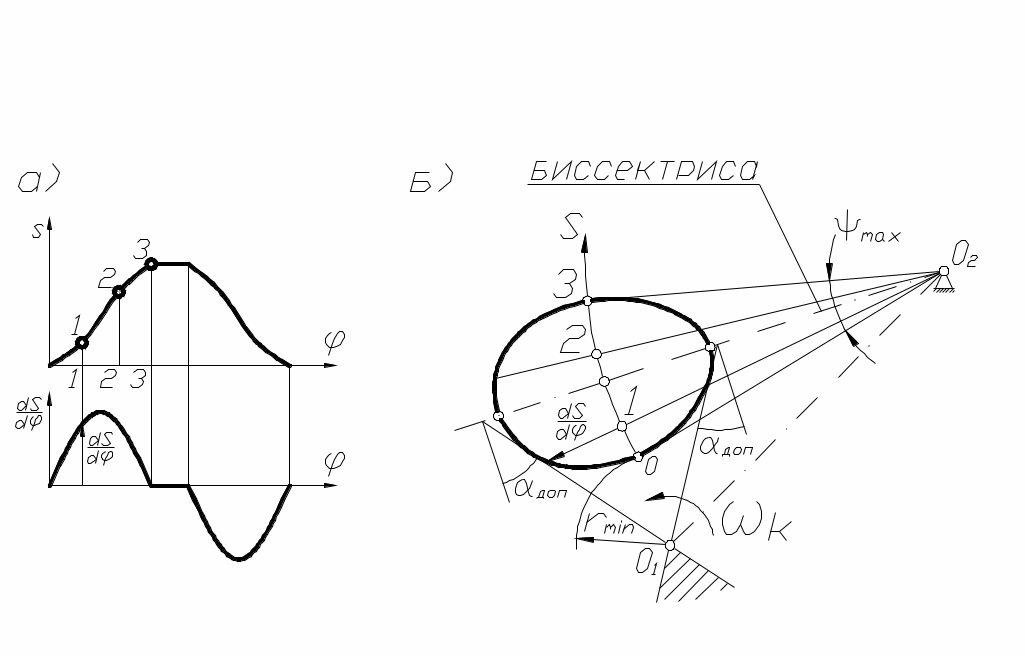
рис. 58
Точки, полученные для нескольких положений коромысла, соединяют плавной кривой и строят допускаемую зону размещения центра вращения кулачка, которую приближённо можно получить, проведя касательные к диаграмме S(dS/dφ) под углами 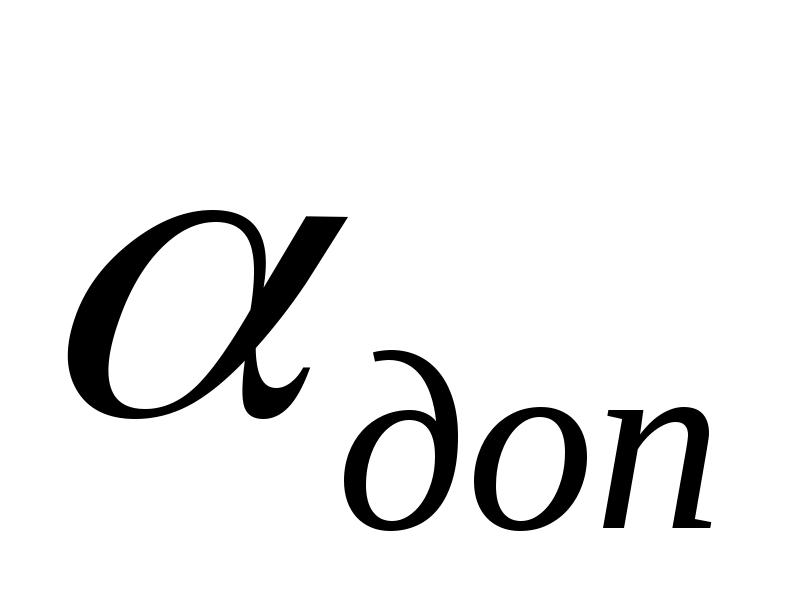 , образованными биссектрисой угла Ψmax и перпендикулярами к ней (см. рис. 58, б). Выбранное положение центра О1 в допускаемой (заштрихованной) зоне определяет величину
, образованными биссектрисой угла Ψmax и перпендикулярами к ней (см. рис. 58, б). Выбранное положение центра О1 в допускаемой (заштрихованной) зоне определяет величину 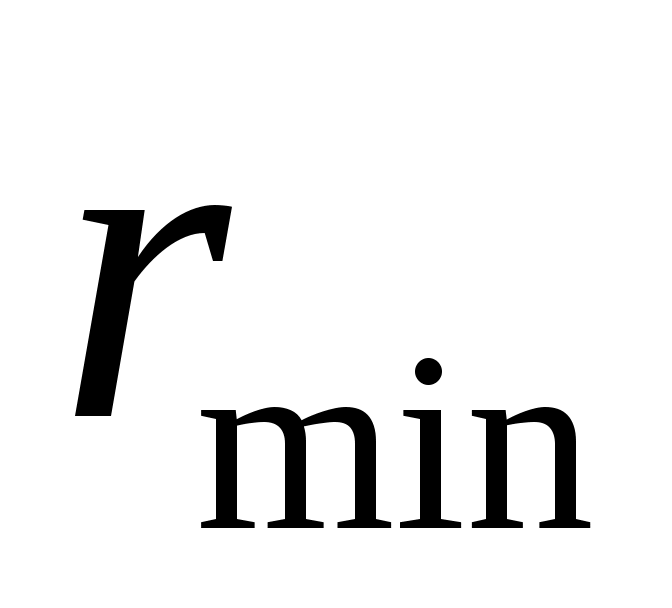 и межцентровое расстояние О1О2 между кулачком и коромыслом.
и межцентровое расстояние О1О2 между кулачком и коромыслом.
7.4.4. Аналитический способ синтеза кулачковых механизмов
При аналитическом методе синтеза вместо диаграмм в графической форме используются аналитические зависимости 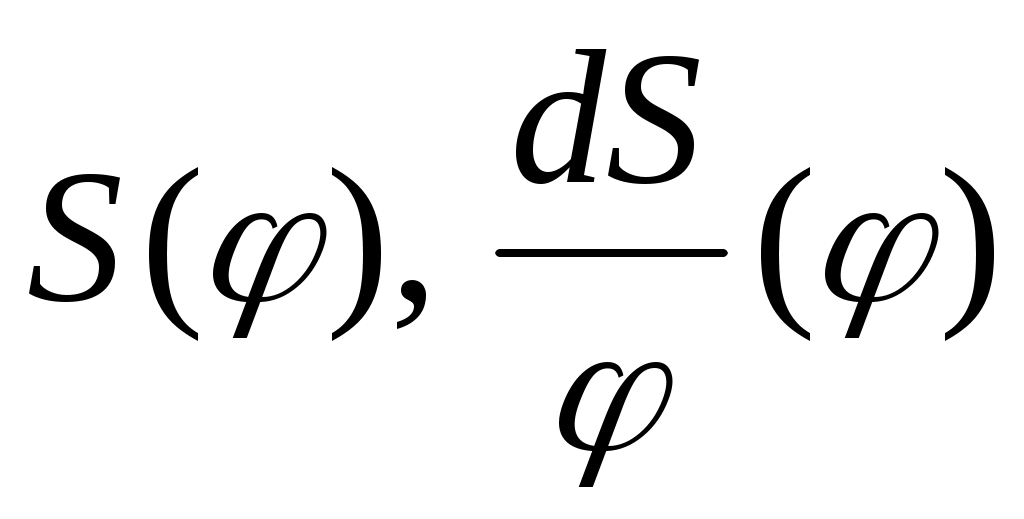 и т. д. Например, для осевого кулачкового механизма с поступательно движущимся толкателем профиль кулачка может быть представлен аналитической зависимостью вида:
и т. д. Например, для осевого кулачкового механизма с поступательно движущимся толкателем профиль кулачка может быть представлен аналитической зависимостью вида:
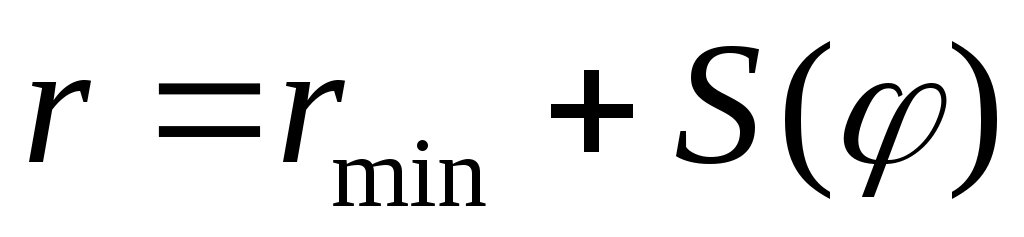 .
.
При заданном rmin и известной зависимости S(φ) можно получить профиль кулачка с любой заданной степенью точности.
7.4.5. Понятие о проектировании пространственных
кулачковых механизмов
Распространённым методом синтеза пространственных механизмов является условная их замена плоским кулачковым механизмом. Тогда задача сводится к синтезу плоского механизма. Например, задача проектирования механизма с поступательно движущимся толкателем и вращающимся кулачком сводится при заданном законе S(φ) к построению развёртки цилиндра, на которой по данным диаграммы строится теоретический и действительный профиль кулачка (рис. 59).
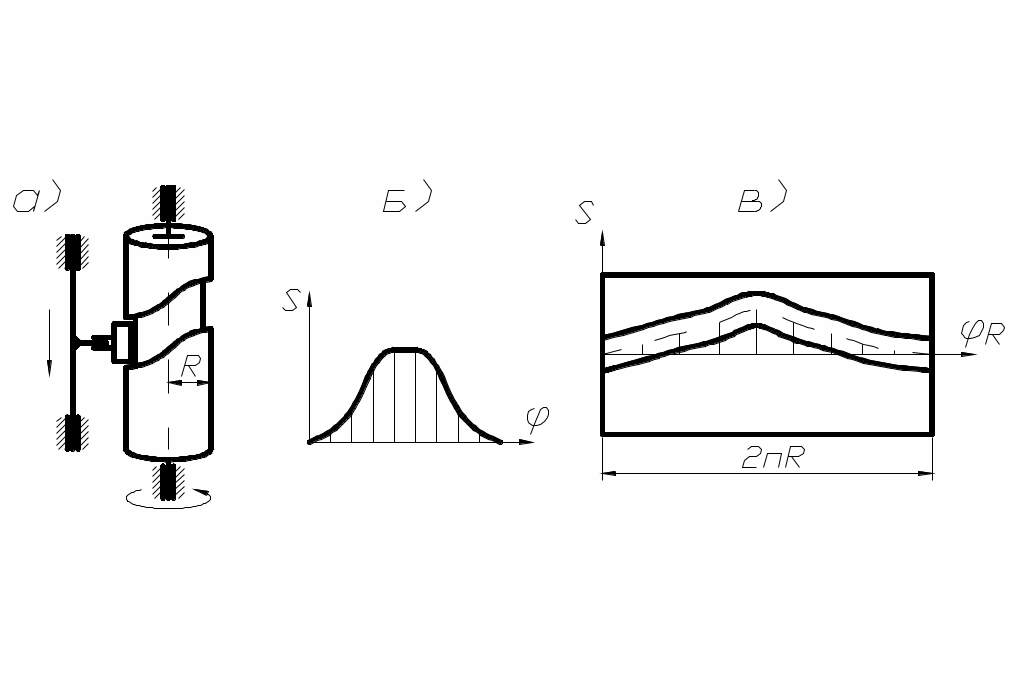
рис. 59
7.4.6. Проектирование кулачковых механизмов
с плоским (тарельчатым) толкателем
В механизме с плоским толкателем угол давления во всех положениях равен нулю (рис. 60, а), поэтому он не может быть использован для определения центра вращения кулачка. В этом случае используют условие выпуклости профиля кулачка ρ>0 (ρ – радиус кривизны профиля).
Заменяя кулачковый механизм стержневым (рис. 60, б), план ускорения которого можно построить из условия подобия (рис. 60, в):
∆КАЕ
∆
7.3. Некоторые вопросы динамического анализа кулачковых механизмов
Условия нормальной работы звеньев кулачкового механизма в существенной степени зависит от угла давления
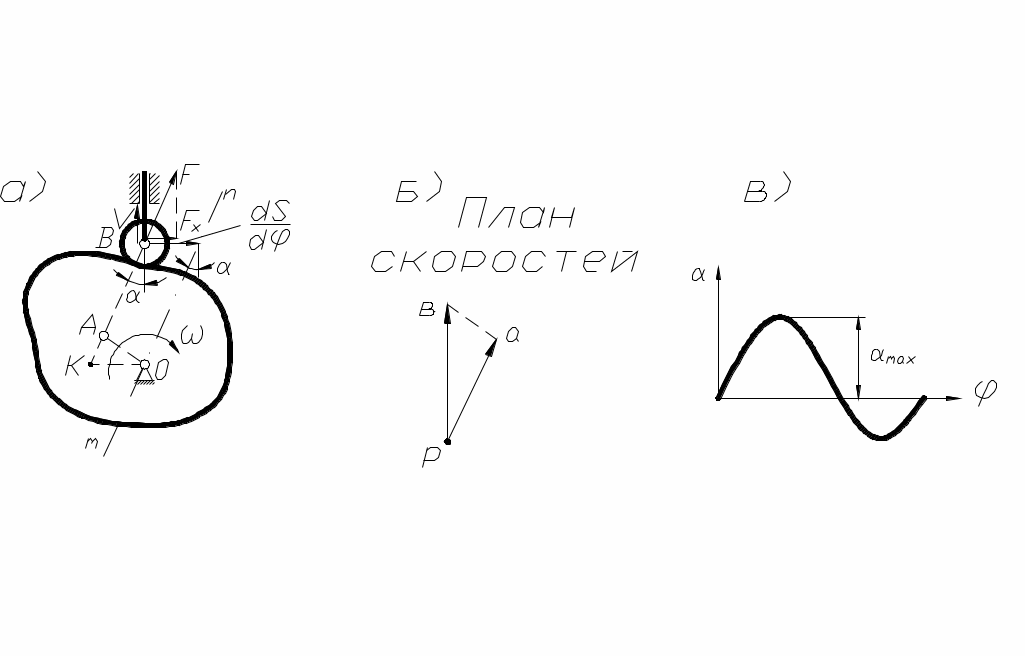
рис. 51
Угол давления – переменная величина, с увеличением которой возрастает опасность заклинивания механизма, т. к. увеличивается составляющая
Обычно величину
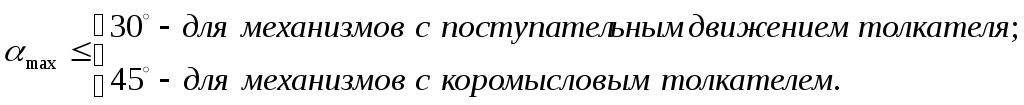
Рассмотрим задачу определения текущего угла
Рассмотрим план скоростей заменяющего механизма (рис. 51, б), где:
πkв,
получим
т. е.

рис. 60
Следовательно, просуммировав две диаграммы S(φ) и
8. Фрикционные и зубчатые механизмы
Фрикционные и зубчатые механизмы предназначены для передачи вращательного движения с одного вала на другой с помощью деталей типа диска в основном цилиндрической формы. При этом, как правило, меняется величина угловой скорости и передаваемого момента, а также их направление. Вал, от которого передаётся движение, называется ведущим, а вал, которому передаётся движение – ведомым.
Оси валов могут быть параллельными, пересекаться или перекрещиваться под различными углами. В первом случае механизм является плоским, в остальных случаях механизмы пространственные.
8.1. Общие сведения о передачах вращения
Если в механизме имеются только ведущие и ведомые валы и отсутствуют промежуточные вращающиеся звенья, то механизм называется передачей. Передача вращения может осуществляться:
1) путём непосредственного соприкосновения двух дисков, жёстко связанных с ведущим и ведомым валами (фрикционная, червячная, зубчатая);
2) посредством промежуточных гибких тел, сцепляющихся с дисками, которые жёстко связаны с ведущим и ведомым валами (ременная, цепная, волновая).
Отношения угловых скоростей вращения обоих валов передачи называется передаточным отношением
Отношения угловой скорости ведущего вала к угловой скорости ведомого называется
передаточным числом
Величина
Любую передачу можно схематично представить в виде двух начальных поверхностей, контактирующих между собой, а плоскую передачу – в виде двух начальных окружностей, перекатывающихся друг по другу без скольжения и контактирующих в полюсе р (рис. 61). Тогда

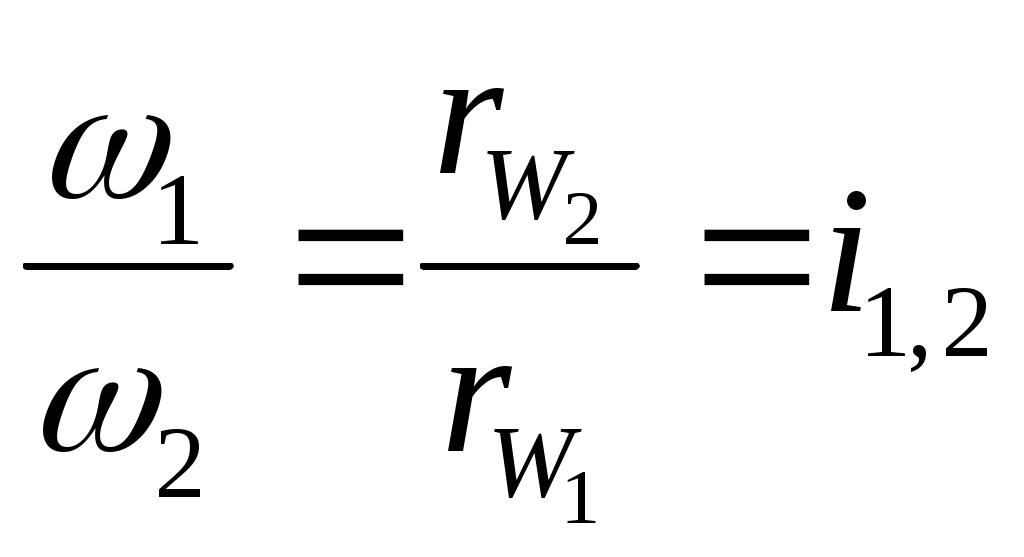 - передаточное число.
- передаточное число.рис. 61
Аналогично можно изобразить ременную или цепную передачи, а также пространственные передачи (рис. 62).
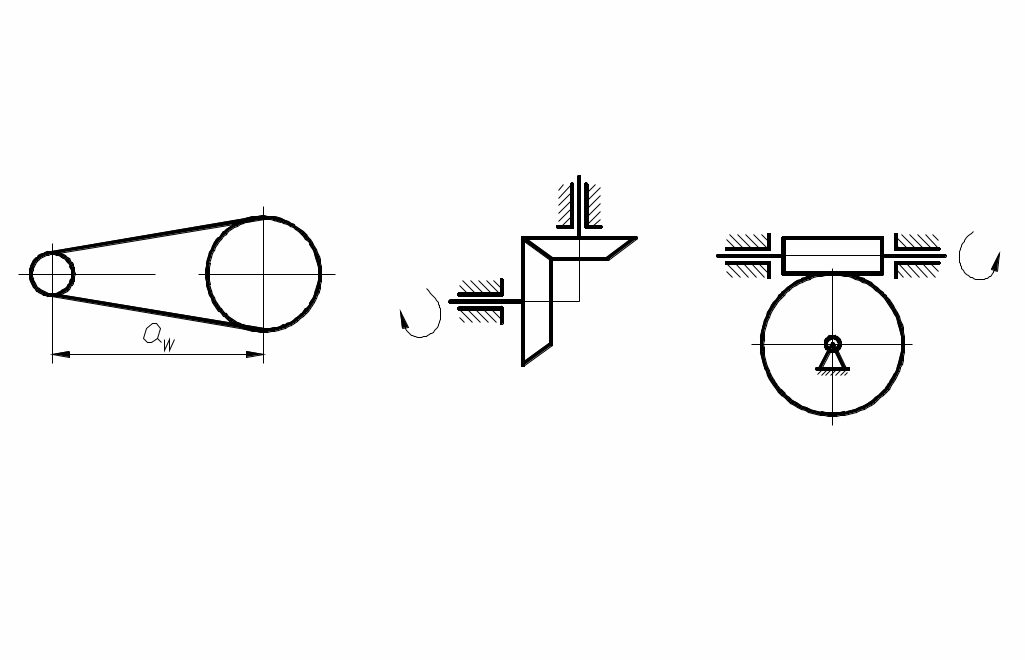
рис. 62
8.2. Фрикционные передачи
О
 дной из наиболее простых и во многих случаях достаточно надёжной является фрикционная передача, состоящая в простейшем случае из двух колёс (катков), закреплённых на ведущем и ведомом валах. Для передачи движения без скольжения необходимо приложить к одному из колёс силу Q, достаточную для возникновения трения в месте контакта (рис. 63), при этом касательная сила их сцепления равна по величине передаваемого окружному усилию.
дной из наиболее простых и во многих случаях достаточно надёжной является фрикционная передача, состоящая в простейшем случае из двух колёс (катков), закреплённых на ведущем и ведомом валах. Для передачи движения без скольжения необходимо приложить к одному из колёс силу Q, достаточную для возникновения трения в месте контакта (рис. 63), при этом касательная сила их сцепления равна по величине передаваемого окружному усилию. рис. 63
Фрикционные передачи могут быть с постоянным и переменным передаточным отношением. Последние называются вариаторами (рис. 64 а, б).

рис. 64
Достоинствами фрикционных передач являются: плавность и бесшумность в работе, простота конструкции, невозможность поломки при резком изменении крутящего момента на одном из валов благодаря возможности проскальзывания катков, возможность бесступенчатого регулирования скоростей.
Недостатками являются: необходимость прижимного устройства, непостоянство передаточного отношения, невозможность передачи значительных крутящих моментов.
В связи с указанными недостатками фрикционные передачи не получили такого широкого распространения как зубчатые.