5.6.6 Определить по рисунку 5.16 какие функции корреляции случайного процесса таковыми не являются



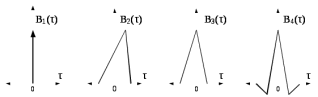
Рис.5.16 – Примеры корреляционных функций

5.6.7 Какие процессы не могут быть эргодическими?

5.6.8 Определить мощность переменной составляющей, мощность постоянной составляющей и мощность всего стационарного эргодического процесса:

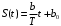
5.6.9 Найти мощность переменной составляющей случайного процесса, представляющего собой пилообразное напряжение с максимальной амплитудой А и периодом повторения Т, усреднением про времени и усреднением по ансамблю.

5.6.10 Приведите примеры случайного процесса с разным разбросом мгновенных значений амплитуд.

5.6.11 Какой параметр нормального закона распределения изменяется при суммировании случайного процесса и постоянной составляющей?

5.6.12 Приведите примеры нормального случайного процесса при прохождения линейной системы.

6. 
   Преобразование сигналов в нелинейных радиотехнических цепях
   

6.1 Спектральный анализ преобразованных сигналов

Для линейной цепи справедлив принцип суперпозиции, из которого вытекает простое и важное следствие – гармонический сигнал, проходя через линейную стационарную систему, остается неизменным по форме, приобретая лишь другую амплитуду и начальную фазу.

Однако именно поэтому линейная стационарная система неспособна обогатить спектральный состав колебаний, поданных на её вход. Это обстоятельство в значительной степени сужает класс полезных преобразований сигналов, которые осуществляются линейными цепями с постоянными параметрами.

Гораздо большими возможностями в этом отношении обладают нелинейные системы, в которых связь между входным сигналом u_вх(t) и выходной реакцией u_вых(t) устанавливается нелинейной функциональной зависимостью:



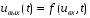
В радиотехнике чаще всего используют следующие вида аппроксимации нелинейных элементов, а именно, кусочно-линейную аппроксимацию и степенную аппроксимацию.

Рассмотрим степенную аппроксимацию нелинейногоэлемента.Представим оператор преобразователя

---

Lв виде степенного полинома:

L(x) = a₀ + a₁ x + a₂ x² + . . .a_k x^k , (6.1)

где х – входное воздействие, а L(x) - выходная реакция цепи на входной сигнал.

Для практики такое выражение неудобно, громоздко, поэтому оно используется для теоретических исследований, потому что, дает возможность рассмотреть все преобразования в общем виде с единой точки зрения. В операторе, аппроксимированном степенным полиномом:

L[x(t)] = a₀ + a₁x(t) + a₂x²(t) + a₃x³(t) + . .+ a_kx^k(t) (6.2)

первые два слагаемые устанавливают линейную связь между входом и выходом как частный случай нелинейной связи. Слагаемые, соответствующие членам полинома со второй и более высоким степеням, описывают явления, связанные с нелинейным преобразованием.

1. 
   Преобразование гармонического сигнала в нелинейной безынерционной цепи.
   

При изучении безынерционной цепи можно не считаться с конечной длительностью реальных сигналов, так как переходные процессы в таких цепях не возникают.

Рассмотрим воздействие моно гармонического сигнала x(t) = Xcos (ωt +φ)

Отклик цепи нелинейной цепи связан с сигналом зависимостью (6.1). Подставим входной сигнал и получим:

L[x(t)]= y(t) = a₀ + a₁Xcos (ωt +φ) + a₂X²cos² (ωt +φ) +

a₃ X³ cos³ (ωt +φ) + . .+ a_k X^k cos^k (ωt +φ) (6.3)

В дальнейшем необходимо избавиться от степенной зависимости, воспользовавшись формулами кратных дуг [4]:







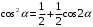
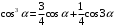
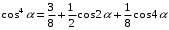
Для третьей степени полинома (6.3) получим выходной сигнал:




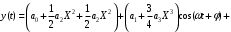
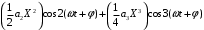
Таким образом, при данной аппроксимации степенного полинома, на выходе образуются новые сигналы, которых не было на входе.

---

Рис.6.1 – Спектры сигналов на входе и на выходе нелинейного элемента.

На рисунке 6.1 показано, каким образом связано влияние степени аппроксимирующего полинома на образование новых гармоник сигнала.

Далее рассмотрим воздействие бигармонического сигнала:

x(t) = X₁ cos (ω₁ t +φ₁)+ X₂ cos (ω₂ t +φ₂) (6.4)

Для этого необходимо воспользоваться не только методом кратных дуг, но и формулами для произведения косинусов:





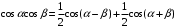
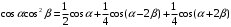
Подставляя выражение (6.4) в (6.3) и ограничиваясь 2-ой степенью полинома, получим:









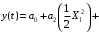
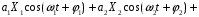
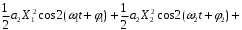
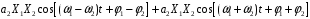
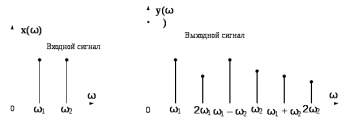
Рис.6.2 – Спектры входного и выходного сигнала при воздействии бигармонического сигнала при использовании полинома 2-ой степени

---

6.1.2 – Метод угла отсечки

Метод угла отсечки используется для гармонического анализа при аппроксимации характеристики нелинейного элемента ломаной линией (рисунок 6.3).

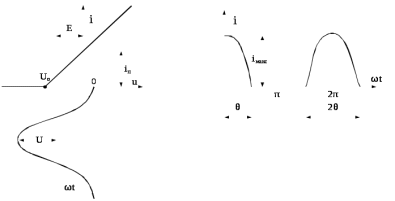Рис. 6.3 – Пояснение процесса по методу трех координатных плоскостей

Пусть характеристика нелинейного элемента состоит из двух отрезков (рисунок 6.3), определяемых выражениями:

i = 0 при u < U₀

i = i_п +Su при u >U₀(6.5)
Здесь U₀– напряжение отсечки или запирания;i_п – ток покоя.

Очевидно, что I_п = S|U₀|

Пусть на вход нелинейного элемента (рисунок 6.3) подается напряжение:

u = E + Ucosωt , (6.6)

где Е – напряжение смещения.

Рабочая точка на характеристике нелинейного элемента выбрана так,

чтобы нелинейное преобразованиеимело место при достаточно больших амплитудах , то есть при выполнении неравенства:

U > |U₀ – E| (6.7)

При выполнении равенства (6.7), как показано на рисунке 6.3 выходной ток протекает только в течение части периода. Половина той части периода, в течение которой ток, называется углом отчески тока и обозначается θ.

i = i_п + SE +SUcosωt.(6.8)

Но при ωt = θ, i = 0 , тогда получаем:

0 = i_п + SE +SUcos θ (6.9)

Вычтем из (6.8) выражение (6.9), получим:

i = SU(cosωt - cos θ)(6.10)

Выражение (6.9) позволяет определить угол отсечки:

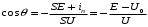(6.11)

Максимальное значение тока получаем из выражения (6.10), приняв ωt=0

I_макс = SU(1 - cos θ).

Следующий шаг, это определение амплитуды гармоник, возникающих при изменении формы сигнала при прохождении нелинейного элемента. Амплитуда гармоник в соответствии с формулами ряда Фурье:



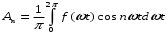
Функция f(ωt), представляющая собой изменение тока во времени, в данном случае является четной, и поэтому ток содержит постоянную составляющую и только косинусоидальные гармонические составляющие, амплитуды А_n которых обозначим через I_n.

Амплитуда первой гармоники:

---

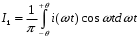
Подставим в эту формулу выражение для i(ωt):




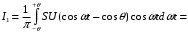
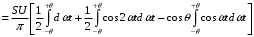
После интегрирования получаем:



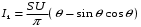
Будем нормировать к максимальному значению тока:



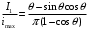
Аналогично составляем и для других гармоник тока:



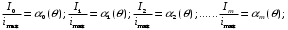
Коэффициенты α называются коэффициентами Берга α_n(θ).

Коэффициенты и находятся по формулам:

,

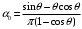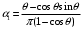
При n ≥2 общая формула для коэффициентов Берга имеет вид

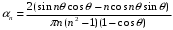(6.12)

Таким образом, коэффициенты Берга зависят только от угла отсечки.

Рассмотрение зависимостей α_n(θ) позволяет сделать выводы:

1. 
   Амплитуды гармоник имеют максимальное значение при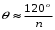
   

2. Амплитуды всех нечетных гармоник (за исключением первой) обращаются в нуль при θ = 90^о, это позволяет избавиться от нежелательных гармонических составляющих и определить угол отсечки нелинейного элемента.

6.2 Преобразование частоты (транспонирование спектра сигнала)

Задача транспонирования спектра заключается в перемещении всего спектра сигнала по оси частот. При данном преобразовании соотношения между комплексными амплитудами составляющих спектра должны быть неизменными, другими словами, информация не должна быть изменена, как показано на рисунке 6.4. На математическом языке это представляется как:

если S₁(t) = A(t)cos[ω_сt+θ(t)], то S₂(t) = KA(t)cos[ω_пр.t+θ(t)].



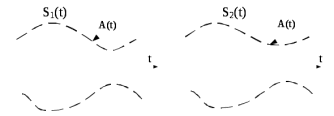
Рис.6.4 – Временные диаграммы сигналов на входе м выходе преобразователя частоты

Рассмотрим целесообразность использования транспонирования спектра при обработке радиосигнала на приеме. При приеме избирательная входная цепь настраивается на частоту принимаемого радиосигнала. Усилитель высокой частоты (УВЧ) усиливает принимаемый сигнала до уровня, при котором можно продетектировать усиленные сигналы без существенных искажений. Каскады УВЧ обладают избирательными свойствами. Общая избирательность входной цепи и усилителя должна быть достаточно высокой. Однако выполнение этих требований, большое усиление и высокая избирательность, затруднено тем, что приемник необходимо настраивать на разные частоты. Эта задача трудновыполнима, так как, надо изменять параметры входной цепи и всех контуров УВЧ, при

---

Смотрите также файлы

• Требования к выполнению реферата.doc

• Предмет, метод и система земельного права. Предметом.docx

• Дипломная работа содержание введение.docx

• Самовосстанавливающегося предохранителя.docx

• Прямая на плоскости и в пространстве.doc