5.2 Числовые характеристики случайного процесса

Для статистической радиотехники наибольшее значение имеют три числовые характеристики, называемые математическим ожиданием, дисперсией и функцией корреляции.

Математическое ожидание случайного процесса (рисунок 5.4) представляет собой неслучайную функцию времени, которая в любой момент времени является математическим ожиданием данного сечения, то есть это кривая геометрического места точек математических ожиданий всех сечений, определяемая как:

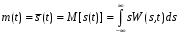(5.1)

- М[ ] – оператор математического ожидания случайной величины, где сплошная линия сверху случайной величины указывает на усреднение по ансамблю реализаций ).



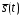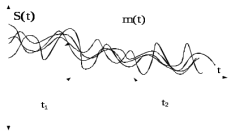
Рис.5.4 – Геометрическая интерпретация математического ожидания

Математическое ожидание квадрата отклонения мгновенных значений случайного процесса от математического ожидания называется дисперсией. Она характеризует мощность случайного процесса и определяется как:

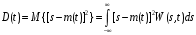(5.2)

Корреляционные функции - характеризуют статистическую или вероятностную связь между мгновенными значениями в сечениях случайных процессов. Корреляционные функции разделяются на следующие типы.

Ковариционная функция – математическое ожидание произведения значений случайного процесса в различные моменты времени t₁ и t₂ (рисунок 5.4):



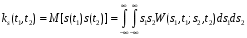
Корреляционная функция B_s(t₁,t₂) (рисунок 5.5) отличается от ковариционной k_s(t₁,t₂) тем, что центрирована:



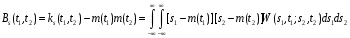
Для центрированного случайного процесса функция корреляции:



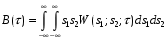
где τ = t₂ – t₁



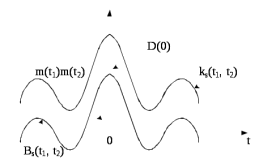
Рис. 5.5 – Корреляционные функции случайных процессов

Нормированная корреляционная функция определяется как [5]:



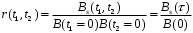
Диапазон изменения -1

---

≤ r ≤ 1

Взаимная корреляционная функция характеризует связь между сечениями различных случайных процессов:



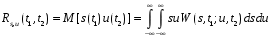
Если процессы независимы, то взаимная корреляционная функция равна нулю.

5.3 Стационарные случайные процессы

Случайные процессы классифицируются согласно рисунка 5.6:



Рис.5.6 – Классификация случайных процессов

Стационарность в узком смысле это когда n – мерная плотность вероятностей не зависит от сдвига всех сечений влево или вправо на одну и ту же величину Δt:

W_n (s₁, t₁; s₂, t₂ ; . . . s_n ,t_n) = W_n (s₁ ,t₁ ±Δt; s₂ ,t₂ ±Δt; . . s_n ,t_n ±Δt;) (5.3)

На основании выражения (5.3) следуют следующие формулы:

1. 
   W₁ (s₁, t₁) = W₁ (s₁ ,t₁ ±Δt) = W₁ (s )
   
2. 
   W₂ (s₁, t₁; s₂, t₂) = W₂ (s₁ ,t₁ ±Δt; s₂ ,t₂ ±Δt) = W₂ (s₁ , s₂ , τ)
   
3. 
   
   
4. 
   
   
5. 
   
   

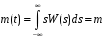
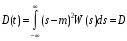
Условие стационарности в узком смысле приводит к тому, что одномерная функция плотностей вероятности не зависит от времени, а числовые характеристики: матожидание и дисперсия тоже не зависят от времени, а функция корреляции зависит от интервала τ = t₂ – t₁.

Процесс называется стационарным в широком смысле, если его числовые характеристики не зависят от времени (условия 3,4) и условие 2.

Случайный стационарный процесс в узком смысле всегда стационарен в широком смысле. Случайный стационарный процесс в широком смысле, не всегда стационарен в узком смысле.
5.4 Эргодические случайные процессы

Эргодическим процессом называется случайный стационарный процесс, для

---

которого числовые характеристики, полученные усреднением по ансамблю и усреднением по одной реализации процесса продолжительностью, равной бесконечностью имеют одинаковые значения.

Определение математического ожидания эргодического процесса:

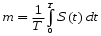(5.3)

Матожидание определяет постоянную составляющую случайного процесса, как показано на рисунке 5.7



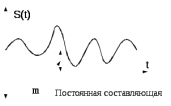
Рис.5.7- Реализация случайного эргодического процесса

Центрированная дисперсия показывает мощность переменной составляющей случайного процесса:

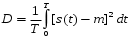(5.4)

Дисперсия случайного процесса показывает мощность всего случайного процесса, то есть мощность переменной и постоянной составляющих случайного процесса:




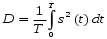
Корреляционная функция является мерой случайной взаимосвязи двух мгновенных значений сигнала, разделенных интервалов времени

τ = t₂ – t₁(рисунок 5.8).



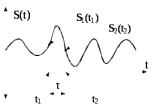
Рис.5.8 – Реализация эргодического случайного процесса

Параметром, характеризующий функцию корреляции является интервал корреляции. Интервалом корреляции называется минимальное расстояние между двумя сечениями, при котором случайные величины можно считать некоррелированными.



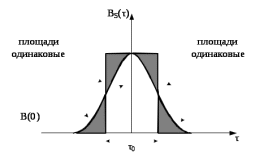
Рисунок 5.9 - Сущность определения интервала корреляции

Как следует из рисунка 5.9 интервал корреляции определяется как:

,

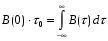
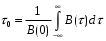то есть τ₀ определяется как основание эквивалентного прямоугольника, площадь которого равна площади под кривой B(τ).

Свойства функции корреляции стационарного процесса:

1. 
   Для эргодического стационарного процесса функция корреляции, рассчитанная усреднением во времени может быть представлена как:
   

---

.

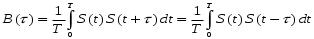То есть функция корреляции – функция симметричная, или четная.

2. 
   Функция корреляции – функция, убывающая:
   

3. 
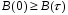
   Полная мощность случайного процесса:
   

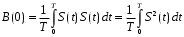
5.5 Нормальный случайный процесс

Нормальным случайным процессом называется процесс, мгновенные значения которого подчиняются нормальному закону распределению вероятностей. Нормальный закон играет огромную роль в радиотехнике, так очень многие процессы подчиняются ему. Он является основополагающим для получения других законов распределения вероятностей в радиотехнических устройствах.

В общем виде нормальный закон плотности распределения вероятностей:



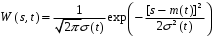
где σ²(t) – дисперсия, квадрат среднеквадратического отклонения мгновенного значения случайного процесса от среднего значения, матожидания m(t). На рисунке 5.10 показано, как изменяется плотность распределения вероятностей при изменении матожидания (среднего значения) и дисперсии.



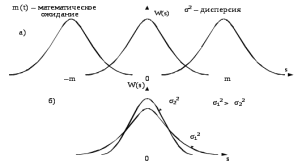
Рис.5.10 - Иллюстрация нормального закона при различных m(t) (а) и различных σ²(t) (б)

Интегральная функция распределения вероятностей:



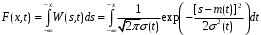
где интеграл в общем виде не берется, поэтому существуют таблицы, но они приводятся для нормированной переменной t:





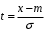
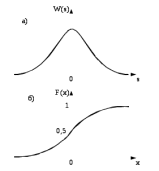
Рис.5.11 – Плотность распределения (а) и соответствующая ей интегральная функция распределения (б) нормального закона



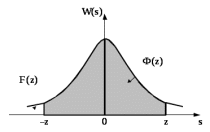
Рис.5.12 – Графическое представление функций F(z) и Ф(z)

На рисунке 5.12 показаны табулируемые функции, математические выражения которых:






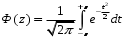
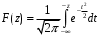
Ниже приведена связь между этими табулированными функциями:

---

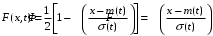
Для нормального закона распределения характерно свойство 3σ:

а)

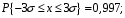
б)

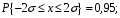
в)

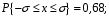
г) ,

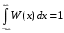Свойства нормального процесса:

1. 
   Стационарность в широком смысле эквивалентна стационарности в узком смысле.
   
2. 
   Условие эргодичности: интеграл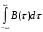 – сходящийся.
   
3. 
   Сечения независимы, если они некоррелированны:
   

4. 
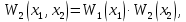
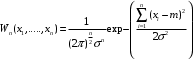
   Линейное преобразование не изменяет закона распределения (вида кривой), изменяются B(τ), σ(t), m(t), τ₀
   
5. 
   Сумма нормального случайного процесса и детерминированной функции не изменяют закона распределения.
   

5.6 Контрольные вопросы и задачи.

5.6.1 Определить в соответствие с рисунком 5.13 область изменения случайной величины



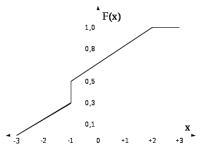
Рис.5.13 – Интегральная функция распределения случайного процесса

5.6.2.В соответствие с рисунком 5.13 построить плотность распределения вероятностей случайной величины.

5.6.3 Найти вероятность попадания случайной величины в интервал

(-3 < x(t) < -1) и (-1 < x(t) < +2), рисунок 5.13.

5.6.4 Определить математическое ожидание и мощность случайного процесса, где плотность распределения вероятностей задана на рисунке 5.14



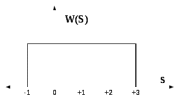
Рис.5.14 – Плотность распределения вероятностей мгновенных значений случайного процесса

5.6.5 Определить математическое ожидание и мощность случайного процесса для плотность распределения вероятностей задана согласно рисунку 5.15 [13]



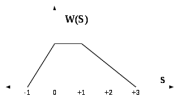
Рис.5.15 – Плотность распределения вероятностей мгновенных значений случайного процесса

---

Смотрите также файлы

• Требования к выполнению реферата.doc

• Предмет, метод и система земельного права. Предметом.docx

• Дипломная работа содержание введение.docx

• Самовосстанавливающегося предохранителя.docx

• Прямая на плоскости и в пространстве.doc