ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 264
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, поэтому о периодичности последовательности «1» и «0» говорить невозможно, т.е. понятие скважности теряет смысл. В данном случае фиксированной остается только длительность одного элемента последовательности .
Рассмотрим более подробно построение спектра сигнала ДФМ при разных индексах модуляции.
Для отыскания математического выражения спектра сигнала ДФМ запишем его в виде [4]:
=
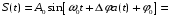
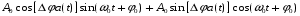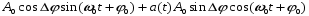
Последнее выражение показывает, что сигнал ДФМ может быть разложен на две квадратурные составляющие: немодулированную несущую с амплитудой A0cosΔφ и манипулированную по фазе составляющую. Используя разложение (4.5), запишем:
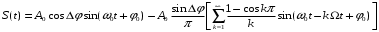
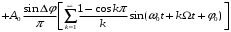(4.7)
При измененииΔφ от 0 до π/2 происходит перераспределение энергии сигнала между несущим колебанием и боковыми составляющими, а при
Δφ = π/2 вся энергия сигнала содержится только в боковых полосах, как показано на рисунке 4.2.
При рассмотрении спектра сигнала ДЧМ следует различать два способа частотной модуляции [4]:
- переключение двух независимых генераторов, имеющих частоты ω1 и ω2
- модуляция частоты одного генератора.
При ДЧМ частота сигнала скачком изменяется на +Δω или - Δω около ω0. Частоты ω1 = ω0 + Δω и ω2 = ω0 - Δω будем называть частотами «нажатия» и «отжатия». По аналогии с аналоговой ЧМ можно ввести индекс дискретной частотной модуляции, определяемый как:
β = Δω/Ω,
где Ω = 2πF = π/τи – круговая частота модуляции при передаче периодической последовательности импульсов, τи – длительность импульса.
Ссылаясь на [4 ] действительная часть сигнала ДЧМ имеет вид:
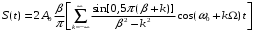(4.8)
При малых значениях индекса частотной модуляции β энергия сигнала сосредоточена в полосе частот сблизи ω0. Следует отметить, что ближайшие боковые гармоники оказываются больше по амплитуде, чем при ДАМ. По мере увеличения β энергия сигнала концентрируется вблизи частот нажатия и отжатия. Интересно отметить, что при нецелых значениях
β, отсутствуют спектральные составляющие на частотах нажатия и отжатия. Амплитуды боковых составляющих при достаточно больших значениях k убываеь обратно пропорционально k2 . При частотной модуляции с разравом фазы спектр сигнала является суперпозицией спектром двух сигналов ДАМ с несущими ω1 и ω2. Амплитуды боковых частот в этом случае убывают обратно пропорционально их номеру k. Таким образом, непрерывность фазы при модуляции приводит к более быстрому затуханию спектральных составляющих, чем при разрывной фазе, что является практически важным с точки зрения взаимных помех, а также определения полосы пропускания приемника.
4.2 Контрольные вопросы и задачи.
4.2.1 Используя выражение ортогональности сигналов ДЧМ:
,
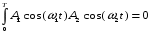определить минимальный частотный сдвиг.
4.2.2 Определить девиацию частоты сигнала ДЧМ, если индекс частотной модуляции соответствует ДЧМ с минимальным сдвигом, а длительность битовой последовательности равна Т.
4.2.3 Как изменится полоса сигнала ДЧМ, если индекс частотной модуляции увеличить в 3 раза?
4.2.4 Каким параметров определяется ширина спектра сигнала с ДАМ?
4.2.5 При каком индексе фазовой модуляции для сигнала с ДФМ гармоника на центральной частоте равна нулю?
4.2.6 Какие изменения происходят со спектром сигнала с ДФМ при индексе фазовой модуляции Δφ = π/2?
4.2.7 При каком значении индекса частотной модуляции спектр ДЧМ состоит из двух спектров ДАМ, где центральные частоты ДАМ соответствуют частотам нажатия и отжатия ДЧМ?
4.2.8 Рассчитать и построить спектр ДФМ при Δφ = π/8, π/4, π/2 для импульсной последовательности со скважностью, равной 2 для первых 5 гармоник.
4.2.9 Рассчитать и построить спектр ДЧМ при значениях частотной модуляции β = 1, 2, 5 для первых 5 гармоник.
4.2.10 Рассчитать и построить спектр ДАМ при значениях фазовой модуляции β = 1, 2, 5 для импульсной последовательности со скважностью, равной 4 для первых 5 гармоник.
5 Основы теории случайных процессов
Теория случайных величин изучает вероятностные явления в «статике», рассматривая их как некоторые зафиксированые результаты экспериментов. Для описания сигналов, которые отображают развивающиеся во времени случайные явления, методы классической теории вероятностей оказываются недостаточными. Подобные задачи изучает часть математики, под названием
теория случайных процессов (сигналов) [11,12].
По определению случайным процессом называется процесс, который описывается случайными функциями времени, где мгновенные значения сигнала являются случайными величинами.
Фиксируя на определенном промежутке времени мгновенные значения случайного сигнала, получаем лишь единственную реализацию случайного процесса. Случайный процесс (рисунок 5.1) представляет собой представляет собой бесконечную совокупность таких реализаций, образующих статистический ансамбль [3].
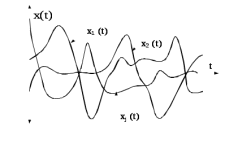
Рис.5.1- Ансамбль реализаций случайного процесса
Например, ансамблем является набор сигналов {x1(t), x2(t), .. }, которые можно наблюдать на выходе разных генераторов шумового напряжения. Случайный характер такого сигнала заключен в невозможности заранее, до опыта, знать мгновенное значение в определенный момент времени.
Реализация случайного процесса – конкретный вид, который приобретает процесс в данном испытании. На рисунке 5.2 представлена реализация процесса, где показаны два сечения - конкретные значения x1 и x2 реализации случайного процесса в некоторый произвольный, но фиксированный момент времениt1и t2. Реализация процесса после опыта уже не является случайной функцией времени. Сечение (рисунок 5.2) – конкретное значение случайного процесса в некоторый произвольный, но фиксированный момент времени t1 и t2.
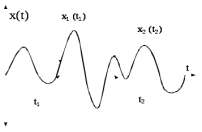
Рис.5.2 - Реализация случайного сигнала
Для определения вероятностных характеристик случайного процесса служат интегральная функция распределения вероятностей F(x,t) и плотность распределения вероятностей W(x,t).
Пусть X(t) – случайный процесс, заданный ансамблем реализаций (рисунок 5.3), а t1 - некоторый произвольный момент времени. Фиксируя мгновенные значения {x1(t1), x2(t1), . . xj(t1), …}, получаемые в отдельных реализациях, осуществляем одномерное сечение данного случайного процесса и наблюдает случайную величину
X(t1).
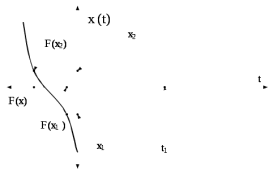
Рис. 5.3 - Ансамбль реализаций сигнала и интегральная функция распределения вероятностей
Далее воспользуемся вероятностной мерой случайного процесса - плотностью распределения W(x,t) или интегральной функцией вероятностей F(x), связанные между собой:
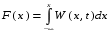(5.1).
Учитывая свойства функции распределения, определим вероятность попадания случайной величины x(t1) в интервал (x2 – x1) в соответствии с рисунком 5.3, как:
Р{x1 < x(t1) < x2} = F(x2) – F(x1).
Свойства интегральной функции распределения и плотности распределения вероятностей следующие [9]:
1. F(∞) = 1
2. F(-∞) = 0
3. F(x) – функция неубывающая
4. Вероятность попадания в интервал Р{-∞ < x(t1) < x2} = F(x2).
5. Р{x1 < x(t1) < ∞} = 1 – F(x1).
6. Р{x1 < x(t1) < x2} = F(x2) – F(x1).
7.
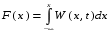
8.
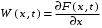
9.
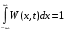условие нормировки
Информация, которую можно извлечь из одномерной плотности распределения вероятностей, недостаточная для того, чтобы судить о характере развития реализаций случайного процесса во времени. Гораздо больше сведений можно получить, располагая двумя сечениями случайного процесса в несовпадающие моменты времени t1иt2. Возникающая при таком мысленном эксперименте двумерная случайная величина {X(t1), X(t2)} описывается двумерной плотностью вероятности W(x1, x2 ,t1 ,t2 ). Такая характеристика случайного процесса позволяет вычислить совместную вероятность того, что реализация процесса случайного процесса при t = t1 проходит в малой окрестности точки x1, а при t
= t2 в малой окрестности точки x2.
Естественным обобщением является n- мерное сечение случайного процесса (n>2), приводящее n- мерной плотности вероятности W(x1, x2, . . . xn, t1, t2, . . tn).
Рассмотрим более подробно построение спектра сигнала ДФМ при разных индексах модуляции.
Для отыскания математического выражения спектра сигнала ДФМ запишем его в виде [4]:
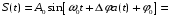
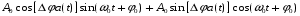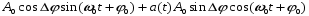
= Последнее выражение показывает, что сигнал ДФМ может быть разложен на две квадратурные составляющие: немодулированную несущую с амплитудой A0cosΔφ и манипулированную по фазе составляющую. Используя разложение (4.5), запишем:
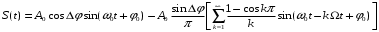
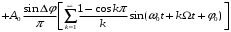(4.7)При измененииΔφ от 0 до π/2 происходит перераспределение энергии сигнала между несущим колебанием и боковыми составляющими, а при
Δφ = π/2 вся энергия сигнала содержится только в боковых полосах, как показано на рисунке 4.2.
При рассмотрении спектра сигнала ДЧМ следует различать два способа частотной модуляции [4]:
- переключение двух независимых генераторов, имеющих частоты ω1 и ω2
- модуляция частоты одного генератора.
При ДЧМ частота сигнала скачком изменяется на +Δω или - Δω около ω0. Частоты ω1 = ω0 + Δω и ω2 = ω0 - Δω будем называть частотами «нажатия» и «отжатия». По аналогии с аналоговой ЧМ можно ввести индекс дискретной частотной модуляции, определяемый как:
β = Δω/Ω,
где Ω = 2πF = π/τи – круговая частота модуляции при передаче периодической последовательности импульсов, τи – длительность импульса.
Ссылаясь на [4 ] действительная часть сигнала ДЧМ имеет вид:
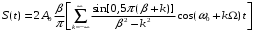(4.8)При малых значениях индекса частотной модуляции β энергия сигнала сосредоточена в полосе частот сблизи ω0. Следует отметить, что ближайшие боковые гармоники оказываются больше по амплитуде, чем при ДАМ. По мере увеличения β энергия сигнала концентрируется вблизи частот нажатия и отжатия. Интересно отметить, что при нецелых значениях
β, отсутствуют спектральные составляющие на частотах нажатия и отжатия. Амплитуды боковых составляющих при достаточно больших значениях k убываеь обратно пропорционально k2 . При частотной модуляции с разравом фазы спектр сигнала является суперпозицией спектром двух сигналов ДАМ с несущими ω1 и ω2. Амплитуды боковых частот в этом случае убывают обратно пропорционально их номеру k. Таким образом, непрерывность фазы при модуляции приводит к более быстрому затуханию спектральных составляющих, чем при разрывной фазе, что является практически важным с точки зрения взаимных помех, а также определения полосы пропускания приемника.
4.2 Контрольные вопросы и задачи.
4.2.1 Используя выражение ортогональности сигналов ДЧМ:
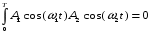, определить минимальный частотный сдвиг.
4.2.2 Определить девиацию частоты сигнала ДЧМ, если индекс частотной модуляции соответствует ДЧМ с минимальным сдвигом, а длительность битовой последовательности равна Т.
4.2.3 Как изменится полоса сигнала ДЧМ, если индекс частотной модуляции увеличить в 3 раза?
4.2.4 Каким параметров определяется ширина спектра сигнала с ДАМ?
4.2.5 При каком индексе фазовой модуляции для сигнала с ДФМ гармоника на центральной частоте равна нулю?
4.2.6 Какие изменения происходят со спектром сигнала с ДФМ при индексе фазовой модуляции Δφ = π/2?
4.2.7 При каком значении индекса частотной модуляции спектр ДЧМ состоит из двух спектров ДАМ, где центральные частоты ДАМ соответствуют частотам нажатия и отжатия ДЧМ?
4.2.8 Рассчитать и построить спектр ДФМ при Δφ = π/8, π/4, π/2 для импульсной последовательности со скважностью, равной 2 для первых 5 гармоник.
4.2.9 Рассчитать и построить спектр ДЧМ при значениях частотной модуляции β = 1, 2, 5 для первых 5 гармоник.
4.2.10 Рассчитать и построить спектр ДАМ при значениях фазовой модуляции β = 1, 2, 5 для импульсной последовательности со скважностью, равной 4 для первых 5 гармоник.
5 Основы теории случайных процессов
-
Вероятностные характеристики случайных процессов
Теория случайных величин изучает вероятностные явления в «статике», рассматривая их как некоторые зафиксированые результаты экспериментов. Для описания сигналов, которые отображают развивающиеся во времени случайные явления, методы классической теории вероятностей оказываются недостаточными. Подобные задачи изучает часть математики, под названием
теория случайных процессов (сигналов) [11,12].
По определению случайным процессом называется процесс, который описывается случайными функциями времени, где мгновенные значения сигнала являются случайными величинами.
Фиксируя на определенном промежутке времени мгновенные значения случайного сигнала, получаем лишь единственную реализацию случайного процесса. Случайный процесс (рисунок 5.1) представляет собой представляет собой бесконечную совокупность таких реализаций, образующих статистический ансамбль [3].
Рис.5.1- Ансамбль реализаций случайного процесса
Например, ансамблем является набор сигналов {x1(t), x2(t), .. }, которые можно наблюдать на выходе разных генераторов шумового напряжения. Случайный характер такого сигнала заключен в невозможности заранее, до опыта, знать мгновенное значение в определенный момент времени.
Реализация случайного процесса – конкретный вид, который приобретает процесс в данном испытании. На рисунке 5.2 представлена реализация процесса, где показаны два сечения - конкретные значения x1 и x2 реализации случайного процесса в некоторый произвольный, но фиксированный момент времениt1и t2. Реализация процесса после опыта уже не является случайной функцией времени. Сечение (рисунок 5.2) – конкретное значение случайного процесса в некоторый произвольный, но фиксированный момент времени t1 и t2.
Рис.5.2 - Реализация случайного сигнала
Для определения вероятностных характеристик случайного процесса служат интегральная функция распределения вероятностей F(x,t) и плотность распределения вероятностей W(x,t).
Пусть X(t) – случайный процесс, заданный ансамблем реализаций (рисунок 5.3), а t1 - некоторый произвольный момент времени. Фиксируя мгновенные значения {x1(t1), x2(t1), . . xj(t1), …}, получаемые в отдельных реализациях, осуществляем одномерное сечение данного случайного процесса и наблюдает случайную величину
X(t1).
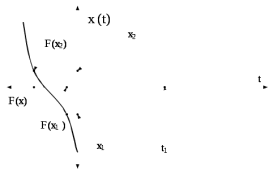
Рис. 5.3 - Ансамбль реализаций сигнала и интегральная функция распределения вероятностей
Далее воспользуемся вероятностной мерой случайного процесса - плотностью распределения W(x,t) или интегральной функцией вероятностей F(x), связанные между собой:
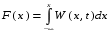(5.1).Учитывая свойства функции распределения, определим вероятность попадания случайной величины x(t1) в интервал (x2 – x1) в соответствии с рисунком 5.3, как:
Р{x1 < x(t1) < x2} = F(x2) – F(x1).
Свойства интегральной функции распределения и плотности распределения вероятностей следующие [9]:
1. F(∞) = 1
2. F(-∞) = 0
3. F(x) – функция неубывающая
4. Вероятность попадания в интервал Р{-∞ < x(t1) < x2} = F(x2).
5. Р{x1 < x(t1) < ∞} = 1 – F(x1).
6. Р{x1 < x(t1) < x2} = F(x2) – F(x1).
7.
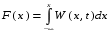
8.
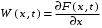
9.
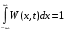условие нормировкиИнформация, которую можно извлечь из одномерной плотности распределения вероятностей, недостаточная для того, чтобы судить о характере развития реализаций случайного процесса во времени. Гораздо больше сведений можно получить, располагая двумя сечениями случайного процесса в несовпадающие моменты времени t1иt2. Возникающая при таком мысленном эксперименте двумерная случайная величина {X(t1), X(t2)} описывается двумерной плотностью вероятности W(x1, x2 ,t1 ,t2 ). Такая характеристика случайного процесса позволяет вычислить совместную вероятность того, что реализация процесса случайного процесса при t = t1 проходит в малой окрестности точки x1, а при t
= t2 в малой окрестности точки x2.
Естественным обобщением является n- мерное сечение случайного процесса (n>2), приводящее n- мерной плотности вероятности W(x1, x2, . . . xn, t1, t2, . . tn).