ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 156
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Проанализируем, как упростятся уравнения Л. Эйлера в случае установившегося движения жидкости. Правые части этих уравнений
; 
и 
представляют собой проекции ускорений движения жидкой частицы на оси х, у и z и являются полными производными по времени от соответствующих проекций скорости ее движения на те же оси.В случае установившегося движения жидкости скорость и ее проекции есть функции лишь координат и не зависят от времени. Это означает, что частные производные от скорости и ее проекций повремени равны нулю:
.Тогда полные производные примут вид:
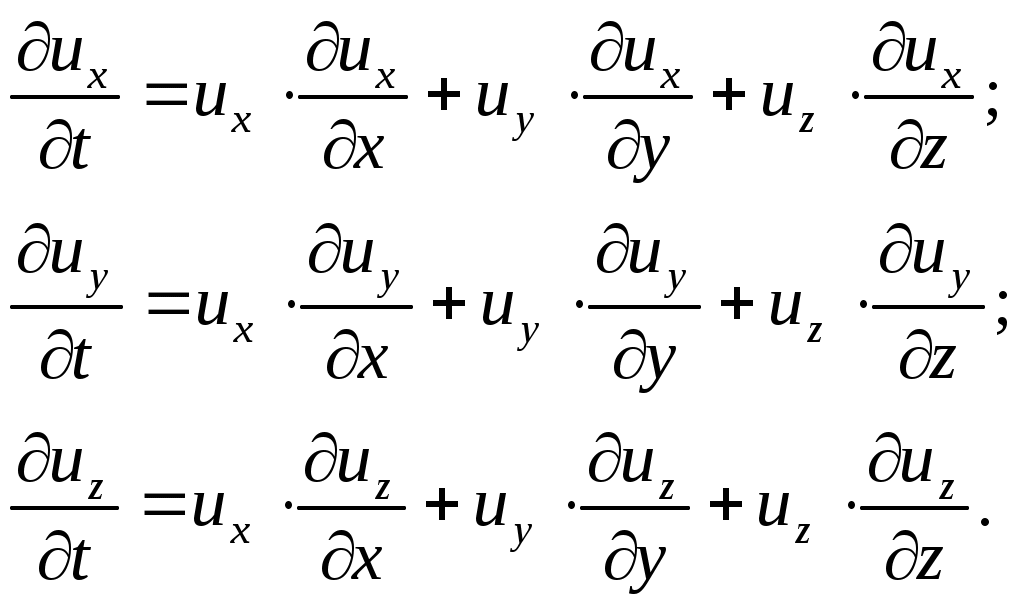
Это обстоятельство мы будем иметь в виду при дальнейших выкладках. Прежде чем перейти к интегрированию уравнений движения идеальной жидкости, примем следующие дополнительные условия:
-
из внешних массовых сил действует лишь сила тяжести; -
гидродинамическое давление является функцией координат и не зависит от времени; -
жидкость является несжимаемой (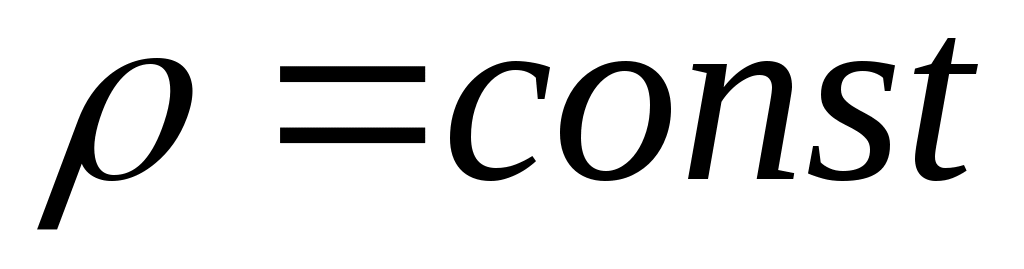
).
Умножим уравнения Л.Эйлера соответственно на
, 
и 
и почленно сложим. При этом будем считать, что , и являются проекциями на координатные оси бесконечно малого участка пути, пройденного частицей жидкости за время 
вдоль линии тока (или траектории, так как мы рассматриваем установившееся движение, при котором линии тока и траектории движения совпадают). Ось z направим вертикально вверх.
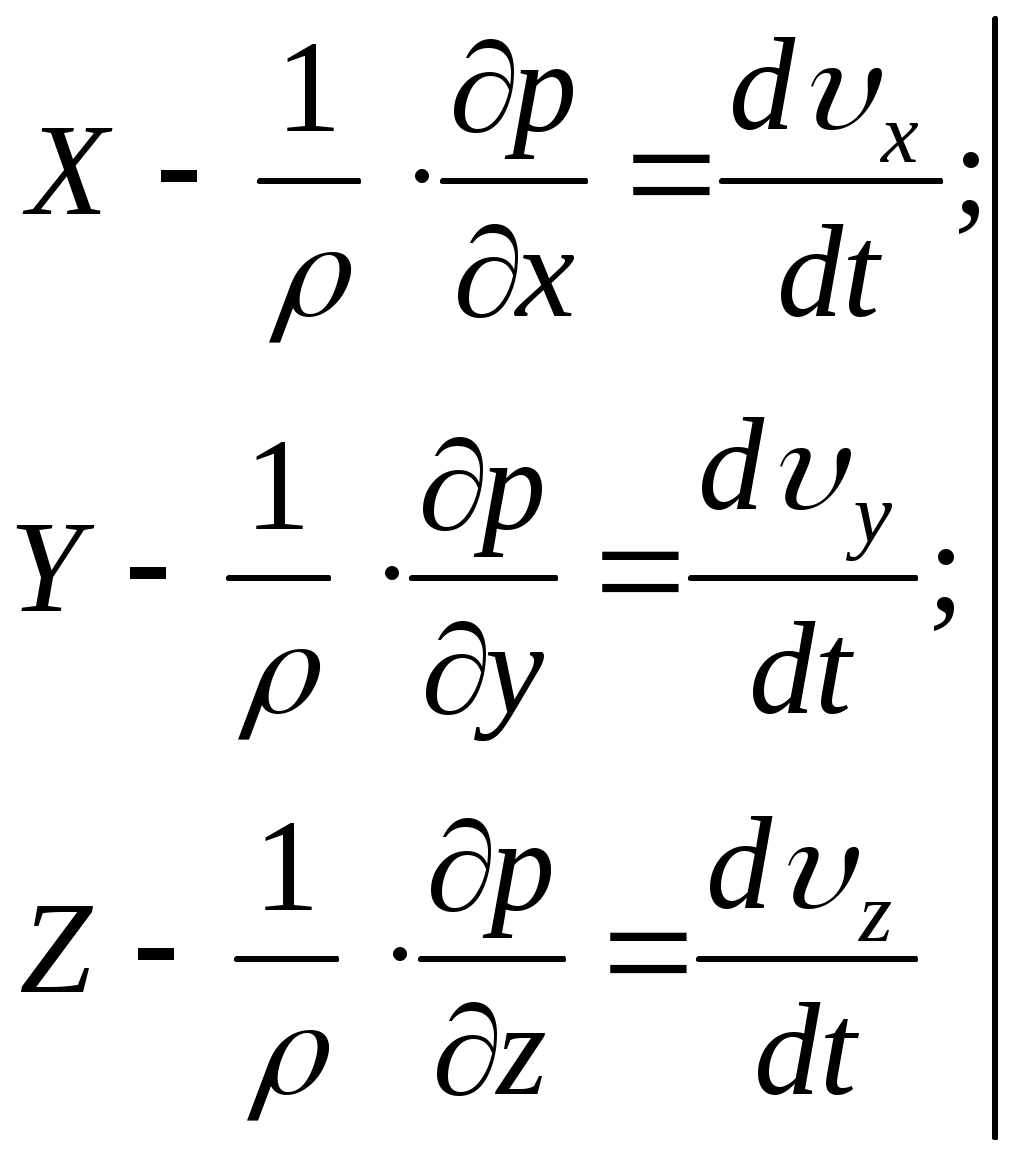
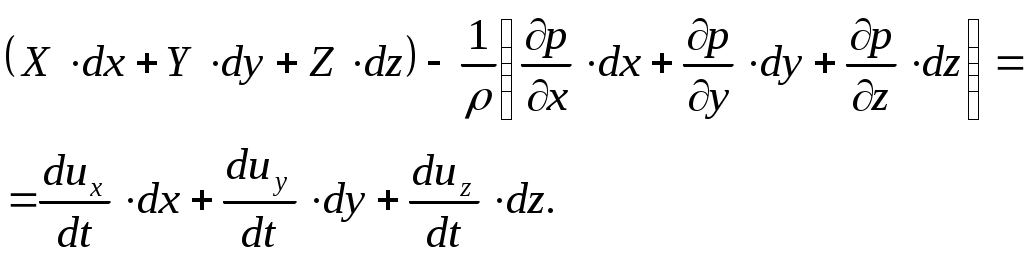(11.10)Проекции единичной массовой силы (в данном случае силы тяжести) примут следующие значения при выбранном направлении осей координат:
; 
; 
.Поэтому первый трехчлен в выражении (11.10) будет равен -
.Второй трехчлен при принятом условии независимости гидродинамического давления от времени, как легко видеть, представляет собой полный дифференциал давления:
.Трехчлен в правой части выражения (11.10) преобразуем следующим образом:
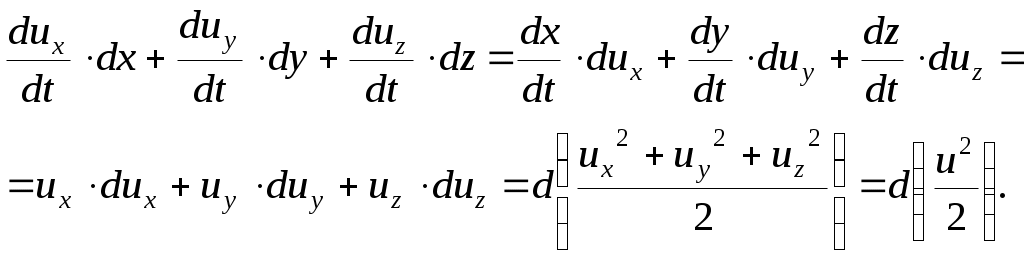
Следовательно, при установившемся движении этот трехчлен представляет собой полный дифференциал от половины квадрата скорости движения частицы вдоль линии тока.
С учетом всего изложенного перепишем уравнение (11.10),
,или
.Деля на g и учитывая, что
, получим:
.Интегрируя это дифференциальное уравнение в полных дифференциалах, придем к следующему результату:
(11.11)Это уравнение называется уравнением Д.Бернулли, оно справедливо при установившемся движении идеальной жидкости и означает, что сумма трех входящих в него величин есть величина постоянная для данной линии тока (траектории). Особо подчеркиваем, что для всякой иной линии тока (траектории) значение этой постоянной может быть другим.
Пусть в сечении 1-1 элементарной струйки площадь ее живого сечения равна
, движения жидкости в этом сечении 
, а гидродинамическое давление в этом сечении равно 
. Соответствующие величины для живого сечения этой же струйки 2-2 обозначим 
, 
и 
(рис. II.00).Превышение центров тяжести площадей живых сечений 1-1 и 2-2 над произвольно выбранной горизонтальной плоскостью сравнения обозначим
и 
.Масса жидкости, прошедшей за время
через сечение 1-1, привносит с собой в отсек элементарной струйки 1-1 и 2-2 кинетическую энергию в размере:
.Эта же масса жидкости обладает и запасом потенциальной энергии, равной:
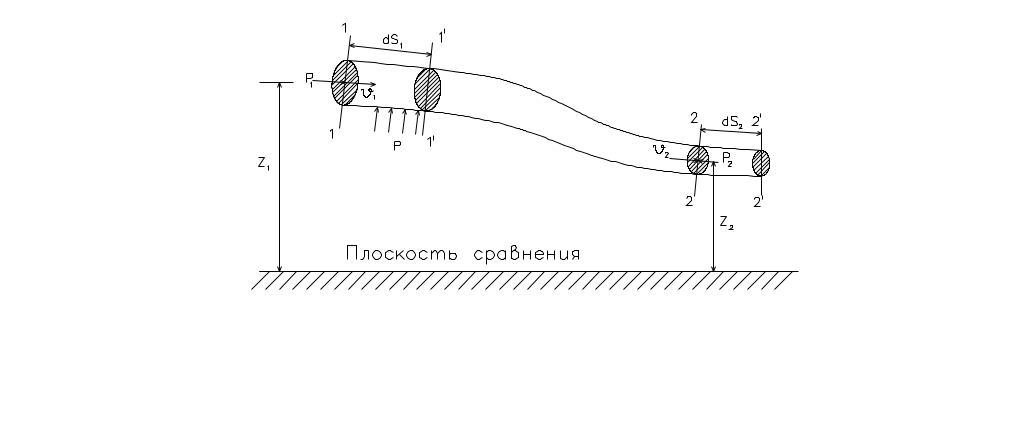
Рис. II.00
Таким образом, через сечение 1-1 за время
жидкостью привносится энергия, равная сумме перечисленных видов энергий:
Аналогично получим, что энергии, выносимая жидкостью за это же время через сечение 2-2, будет равна:
Применяя закон сохранения энергии к рассматриваемому случаю, можем утверждать, что энергия, внесенная жидкостью за время
в отсек элементарной струйки, должна быть равна энергии, вынесенной жидкостью из этого же отсека за то же время, т.е. 
или
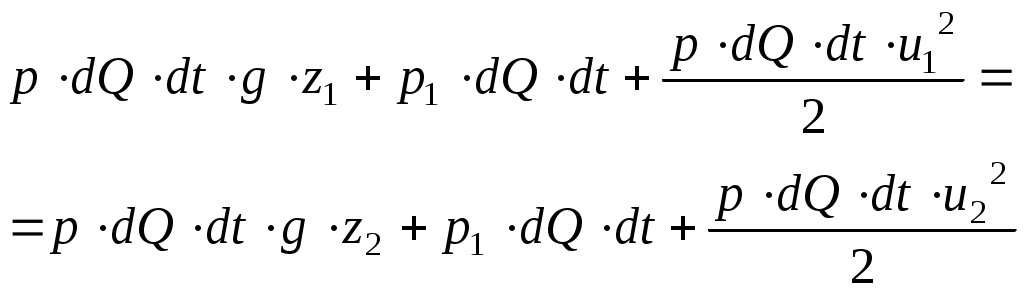
Отнесем полученное равенство вносимых и выносимых жидкостью полных энергией к единице веса жидкости, для чего поделим полученное выражение на
, помня, что 
. В результате получим:
(11.12)Это и есть уравнение Д.Бернулли.
Энергию, приходящуюся на каждую единицу веса жидкости, впредь будем называть удельной энергией и обозначать
. Тогда уравнение (11.12) можно переписать в виде:
. (11.13)2.4. Геометрический и энергетический смысл уравнения Д.Бернулли
Все члены, входящие в уравнение Д.Бернулли, имеют линейную размерность, поэтому их принято называть высотами. Соответственно общеприняты следующие названия для этих членов:
- геометрическая или геодезическая высота;
- пьезометрическая высота или высота давления;
- скоростная высота или скоростной напор.Легко усмотреть следующий геометрический смысл уравнения Д.Бернулли, который заключается в том, что при установившемся движении идеальной жидкости сумма трех высот (геометрической, пьезометрической и скоростной) не меняется вдоль данной элементарной струйки. Это положение наглядно иллюстрируется II.01.
Можно трактовать смысл отдельных членов уравнения Бернулли иначе. Выше было показано, что сумма
представляет собой удельную энергию жидкости. В соответствии с этим можно считать, что:
- есть удельная энергия положения;
- есть удельная энергия давления;
- есть удельная кинетическая энергия.Энергетический смысл уравнения Бернулли заключается в том, что при установившемся движении идеальной жидкости сумма удельных энергий положения, давления и кинетической не меняется вдоль данной элементарной струйки.
Очевидно, двучлен
представляет собой удельную потенциальную кинетическую энергию движущейся частицы жидкости. Полная удельная энергия (т.е. потенциальная + кинетическая) 
называется гидродинамическим напором и обозначается 
. Таким образом, уравнение Бернулли показывает, что при установившемся движении идеальной жидкости для данной струйки гидродинамический напор есть величина постоянная.
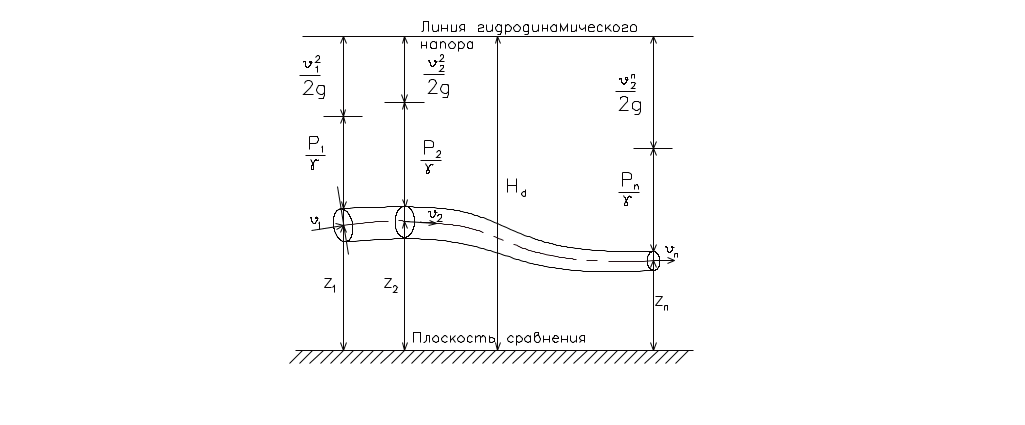
Рис. II.01
На графике линия гидродинамического напора изображается горизонтальной линией.