Файл: Упр 1 Приведите примеры технических устройств, действие которых основано на открытии радиоактивности, электромагнитных волн, ультразвука, реактивного движения.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 135
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Найти h.
Решение.
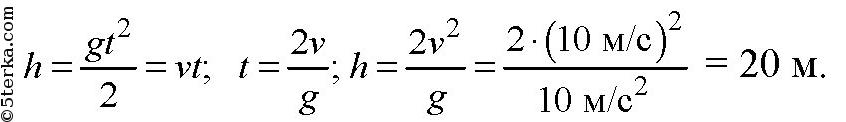
3. Под каким углом к горизонту брошено тело, если в точке максимального
подъема радиус кривизны превышает высоту полета в 2 раза.
точке максимального подъёма: g = Vx^2/r. => Vx^2 = gr
По условию, радиус кривизны r = 2h. => Vx^2 = 2gh.
Высота максимального подъема: h = Vy^2/2g => Vy^2 = 2gh.
Сравнивая выражения для Vx и Vy, можно сделать вывод, что Vx = Vy.
Следовательно, тело было брошено под углом 45 градусов к горизонту
4. Из миномета, расположенного у основания горы, ведется обстрел объектов
противника, расположенных на плоском склоне горы. Склон составляет
с горизонтом угол 30°. Ствол миномета установлен под углом 60° к гори-
зонту, мины вылетают со скоростью 90 м/с. Определите минимальное
расстояние между минометом и местом падения мины
я бы направил одну из осей вдоль ЗЕМЛИ (х) , а вторую перпендикулярно СКЛОНУ (у) . тогда в проекции на ось у мы сразу найдем время полета: v_y=v sin 30=v/2 a_y=-g cos 30 = -sqrt(3)g/2 приравниваем vt/2-gt^2/4sqrt(3)=0 и получаем t=2v/sqrt(3)g (второе решение соответствует вылету снаряда) . теперь записываем для второй проекции: скорость вдоль земли будет равна v sin 30 = v/2 x=tv_x=vt/2=v^2/g а дальше делим на cos 30, чтобы найти расстояние вдоль склона: x=2v^2/3g x=2*90^2/3*10=540
Упр7
1. Какую силу нужно приложить, чтобы магнит массой 50 г, прилипший
к стальной вертикальной плите, равномерно переместить вертикально
вверх? Для равномерного движения магнита вертикально вниз приклады-
вают силу 1,5 Н.
Дано:
m = 50 г = 0,050 кг
F₁ = 1,5 Н
____________
F₂ - ?
Направим ось OY вертикально вверх
Тогда при движении вниз:
- F₁ - m·g + Fтр = 0 (1)
При движении вверх:
F₂ - m·g - Fтр = 0 (2)
Сложим уравнения (1) и (2)
F₂ - F₁ - 2·m·g = 0
F₂ = F₁ + 2·m·g
F₂ = 1,5 + 2·0,050·10 = 2,5H
2. На гладкой наклонной плоскости с углом наклона 30° находится тело
массой 50 кг, на которое действует сила 294 Н горизонтально направ-
ленная. Определите ускорение тела в случае, если указанная сила дей-
ствует: а) слева направо; б) справа налево; g = 10 м/с 2
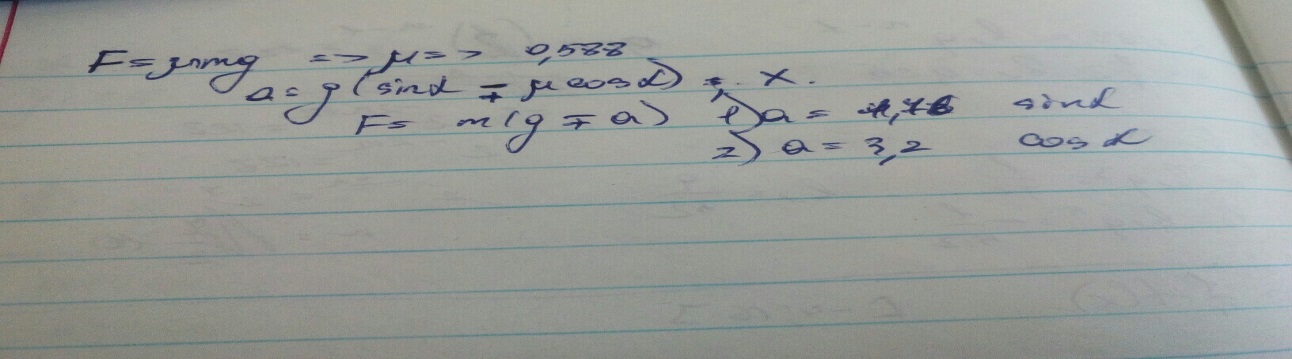
3. К потолку лифта, движущегося вертикально вверх с ускорением 1,2 м/с 2 ,
прикреплен динамометр, к которому подвешен блок, свободно вращаю-
щийся вокруг горизонтальной оси. Через блок перекинута нить, к концам
которой привязаны грузы массами 0,2 кг и 0,3 кг. Определите показания
динамометра, считая блок и нити невесомыми, g = 10 м/с 2
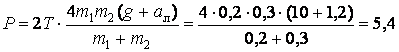
1 час 25 минут
упр9
1. Чему равен момент инерции для тела массой 200 г, вращающегося
по окружности радиусом 10 см, в момент, когда его скорость от нулевого
значения изменилась до значения 1,4 м/с? Определите среднее значение
угловой скорости.
Момент инерции (считаем тело точкой):
J = m*R²=0,2*0,1² = 0,002 кг*м²
Изменение момента импульса:
ΔL = J*Δω
Найдем изменение угловой скорости
ΔV = Δω*R
Δω=ΔV/R = 1,4/0,1= 14 c⁻¹
Тогда
ΔL = 0,002*14 = 0,028 кг*м/с²
2. Определите момент силы, приводящей автомобиль массой 2 т к ускорен-
ному движению по закругленному участку пути радиусом 20 м. Угловое
ускорение автомобиля 0,05 рад/с
Дано:
m = 2 т = 2000 кг
R = 0,02 км = 20 м
ε = 0,05 рад/с²
___________
M - ?
Момент силы:
M = J·ε
Считаем автомобиль материальной точкой. Тогда момент инерции автомобиля:
J = m·R²
Получаем:
M = J·ε = m·R²·ε
M = 2000·(20)²·0,05 = 40 000 Н·м или 40 кН·м
4. Диск массой 2 кг катится без проскальзывания по гори-
зонтальной плоскости со скоростью 4 м/с. Определите его
кинетическую энергию
Дано:
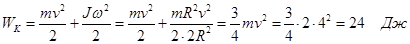
Упр 10
1. Определите момент импульса тела массой 0,1 кг, вращающегося по окруж-
ности радиусом 2 м в горизонтальной плоскости с угловой скоростью 2 π рад/с.
2. Определите момент силы, способной увеличить момент импульса тела
массой 0,1 кг, вращающегося по окружности радиусом 2 м в горизонтальной
плоскости с угловой скоростью 2 π рад/с, вдвое в течение одного оборота.
3. Определите момент силы, совершившей работу 3,14 Дж при перемещении
тела по окружности на φ = 30°

4. Две гири массой 0,2 кг и 0,1 кг соединены нитью и перекинуты через блок
массой 0,1 кг. Определите ускорение, с которым движутся гири, и натя-
жения нитей. Блок считать однородным диском. Трением пренебречь
a=g*(m2-m1)/(m2+m1)-ускорение грузов
из уравнения 1 системы получим T=m1g+m1a
из уравнения 2 получим T=m2g+m2a
T=2g*((m1*m2)/m2+m1))- сила натяжения нити!
m2-2 кг
m1-1 кг
g=10 м /с
считайте!
5. На барабан массой 9 кг намотан шнур, к концу которого привязан груз
массой 2 кг. Определите ускорение, с которым движется груз. Барабан
считать однородным цилиндром, трением пренебречь
Потенциальная энергия груза Ep = m · g · h, которая переходит в кинетическую энергию:
m · g · h = (m · v²) / 2 + (J · ω²) / 2
Момент инерции J = (m₀ · R²) / 2
Угловая скорость ω = ν / R
R - радиус барабана
m₀ - масса барабана
Подставляем в первое уравнение;
m · g · h = (m · v²) / 2 + (m₀ · v²) / 4
Заменим h через h = (a · t²) / 2 и v = a · t
Получим
a = (2 · m · g) / (m₀ + 2 · m) = (2 · 2 кг · 9,8 м/с²) / (9 кг + 2 · 2 кг) ≈ 3 м/с²
упр 11
1. Бревно длиной 12 м можно уравновесить в горизонтальном положении
на подставке, отстоящей на 3 м от его толстого конца. Если же подставка
находится в 6 м от толстого конца, и на тонкий конец сядет рабочий массой
60 кг, то бревно снова будет в равновесии. Определите массу бревна.
Дано:
L = 12 м
x = 3 м
R = 6 м
---------------
М - ?
бревном и человеком равны по модулю, поэтому если считать что человек сидит с самого края доски
Тогда
mgR = Mgh
mR = M( R - x )
M = ( mR )/( R - x )
M = ( 60 * 6 )/( 6 - 3 ) = 120 кг
2. К концам стержня массой 10 кг и длиной 40 см подвешены грузы массами
40 кг и 10 кг. Где необходимо подпереть стержень, чтобы он находился
в равновесии?
М = 10кг; I = 40см = 0,4м; m1 = 40кг; m2 = 10кг; х-?
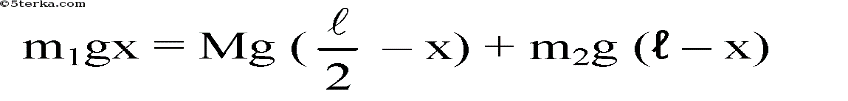
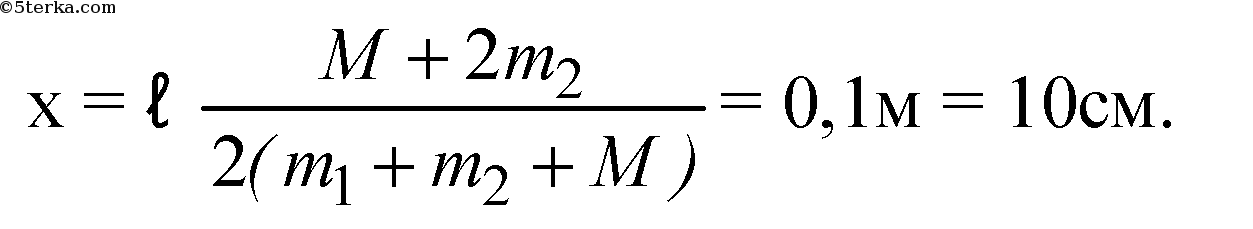
3. Одна половина цилиндрического стержня состоит из стали, другая –
из алюминия. Определить положение центра тяжести, если длина стержня
30 см.
Дано:
L=30 см;
ρ₁=7800 кг/м³;
ρ₂=2700 кг/м³;
____________
Найти:
Решение:
Обозначим площадь поперечного сечения за S, тогда массы половинок стержня:
Решение.
3. Под каким углом к горизонту брошено тело, если в точке максимального
подъема радиус кривизны превышает высоту полета в 2 раза.
точке максимального подъёма: g = Vx^2/r. => Vx^2 = gr
По условию, радиус кривизны r = 2h. => Vx^2 = 2gh.
Высота максимального подъема: h = Vy^2/2g => Vy^2 = 2gh.
Сравнивая выражения для Vx и Vy, можно сделать вывод, что Vx = Vy.
Следовательно, тело было брошено под углом 45 градусов к горизонту
4. Из миномета, расположенного у основания горы, ведется обстрел объектов
противника, расположенных на плоском склоне горы. Склон составляет
с горизонтом угол 30°. Ствол миномета установлен под углом 60° к гори-
зонту, мины вылетают со скоростью 90 м/с. Определите минимальное
расстояние между минометом и местом падения мины
я бы направил одну из осей вдоль ЗЕМЛИ (х) , а вторую перпендикулярно СКЛОНУ (у) . тогда в проекции на ось у мы сразу найдем время полета: v_y=v sin 30=v/2 a_y=-g cos 30 = -sqrt(3)g/2 приравниваем vt/2-gt^2/4sqrt(3)=0 и получаем t=2v/sqrt(3)g (второе решение соответствует вылету снаряда) . теперь записываем для второй проекции: скорость вдоль земли будет равна v sin 30 = v/2 x=tv_x=vt/2=v^2/g а дальше делим на cos 30, чтобы найти расстояние вдоль склона: x=2v^2/3g x=2*90^2/3*10=540
Упр7
1. Какую силу нужно приложить, чтобы магнит массой 50 г, прилипший
к стальной вертикальной плите, равномерно переместить вертикально
вверх? Для равномерного движения магнита вертикально вниз приклады-
вают силу 1,5 Н.
Дано:
m = 50 г = 0,050 кг
F₁ = 1,5 Н
____________
F₂ - ?
Направим ось OY вертикально вверх
Тогда при движении вниз:
- F₁ - m·g + Fтр = 0 (1)
При движении вверх:
F₂ - m·g - Fтр = 0 (2)
Сложим уравнения (1) и (2)
F₂ - F₁ - 2·m·g = 0
F₂ = F₁ + 2·m·g
F₂ = 1,5 + 2·0,050·10 = 2,5H
2. На гладкой наклонной плоскости с углом наклона 30° находится тело
массой 50 кг, на которое действует сила 294 Н горизонтально направ-
ленная. Определите ускорение тела в случае, если указанная сила дей-
ствует: а) слева направо; б) справа налево; g = 10 м/с 2
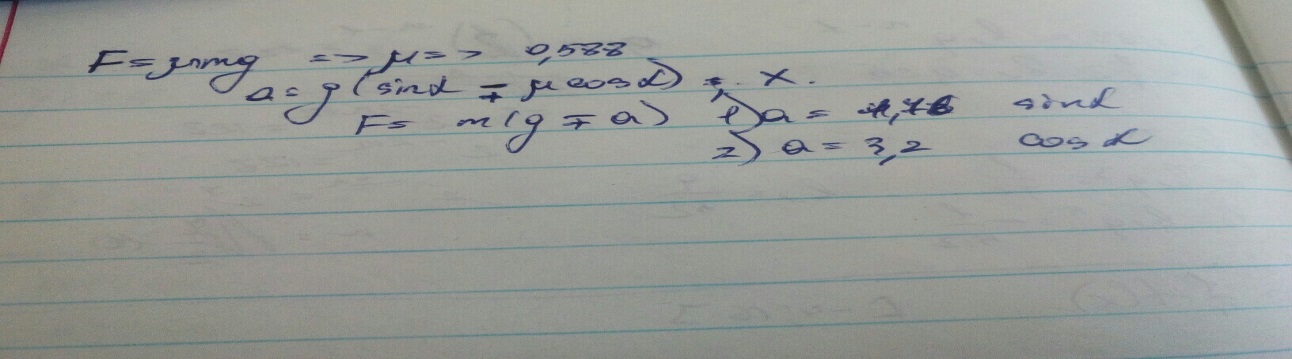
3. К потолку лифта, движущегося вертикально вверх с ускорением 1,2 м/с 2 ,
прикреплен динамометр, к которому подвешен блок, свободно вращаю-
щийся вокруг горизонтальной оси. Через блок перекинута нить, к концам
которой привязаны грузы массами 0,2 кг и 0,3 кг. Определите показания
динамометра, считая блок и нити невесомыми, g = 10 м/с 2
| Дано: m1 = 0,2 кг m2 = 0,3 кг ал = 1,2 м/с2 g = 10 м/с2 | Решение: | | |
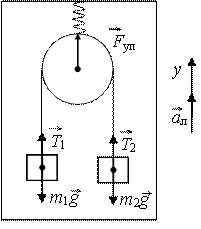 | По условию задачи нить невесома и нерастяжима. Массой блока пренебрегаем. Тогда и . Расставим силы, действующие на грузы, и запишем для каждого тела свое уравнение динамики. В скалярной форме (с учетом, что Т1 = Т2 = Т): Т – m1g = m1(a + a л); (1) | | |
| Р = ? | | ||
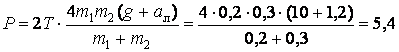
Упр8
1. Ракета-носитель массой 33 т приближаетсяк Международной космической станции массой 410 т. Определите силу притяжения
в момент, когда расстояние между их центрами масс уменьшилось до 100 м.
Космический корабль массой 8 т приблизился к орбитальной космической станции массой 20 т на расстояние 100 м. Найти силу их взаимного притяжения.
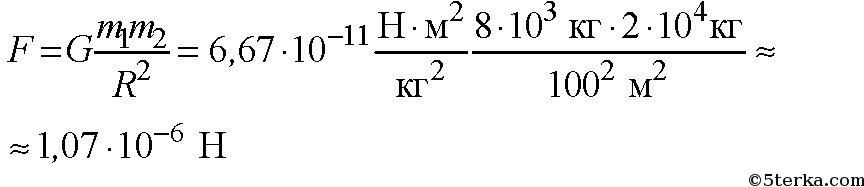
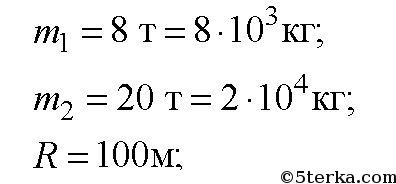
2. На каком расстоянии от поверхности Марса сила взаимодействия меж-
планетной станции Маринер-9 массой 1000 кг с планетой была равна
1,78 кН? Масса Марса равна 6,4 ∙ 10 23 кг, радиус 3400 км
В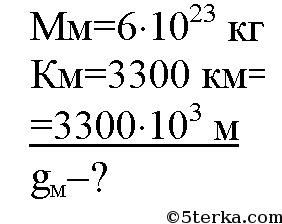 ычислите ускорение свободного падения тел вблизи поверхности Марса. Масса Марса равна 6⋅1023 кг, его радиус 3300 км.
ычислите ускорение свободного падения тел вблизи поверхности Марса. Масса Марса равна 6⋅1023 кг, его радиус 3300 км.
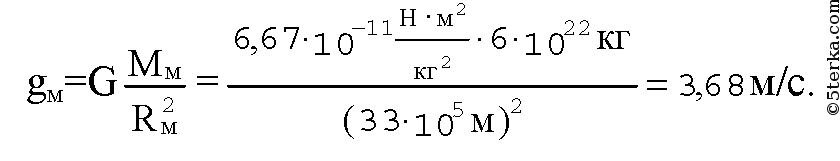
3. Среднее расстояние между центрами Земли и Луны равно 60 земным
радиусам, а масса Луны в 81 раз меньше массы Земли. В какой точке
прямой, соединяющей их центры, следует поместить тело, чтобы оно
притягивалось к Земле и Луне с одинаковыми силами?
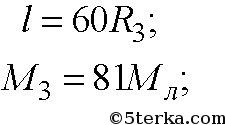
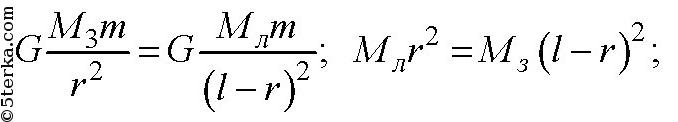
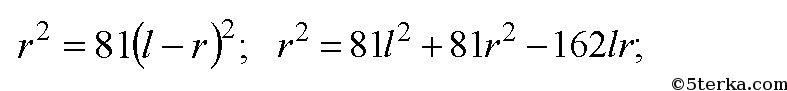
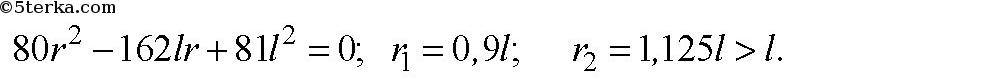
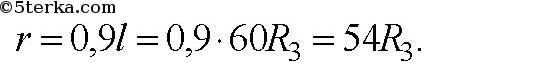
4. Определите силу притяжения шарика массой m и однородного шара,
внутри которого есть сферическая плоскость радиусом R/2 (рис. 32).
Радиус шара R, масса M, расстояние между центрами тяжести L
Масса шара, который заполнил бы сферическую полость, равна Mпол=(4/3)πρ(R/2)3=M/8Mпол=(4/3)πρ(R/2)3=M/8, а центр его лежит на расстоянии r−R/2r−R/2 от шарика массы mm. Искомая сила, равная разности сил притяжения сплошного шара и меньшего шара, заполняющего сферическую полость, выразится так: F=GMmr2−G(M/8)m(r−R/2)2=GMm[7r2−8rR+2R28r2(r−R/2)2]F=GMmr2−G(M/8)m(r−R/2)2=GMm[7r2−8rR+2R28r2(r−R/2)2].
6. Определите потенциал гравитационного поля на геостационарной орбите
Земли. Какой потенциальной энергией обладает космический аппарат
спутниковой связи РК KazSat-3 массой 1,3 тонны на этой орбите (рис. 34).
Расстояние от поверхности Земли до орбиты 36000 км. Масса Земли
6 ∙ 10 24 кг, радиус Земли 6400 км
определите кинетическую энергию космической станции при движении по орбите со скоростью 3,07 км/с, если масса станции 10 т.
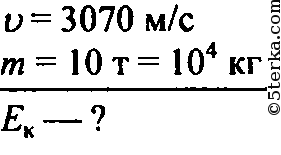
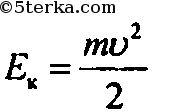
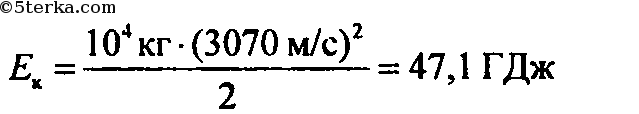
7. Спутник движется вокруг Земли на расстоянии H от ее поверхности.
Радиус Земли R 3 >> H. Определите период обращения спутника. Орбиту
считайте круговой
m*a=mw^2*(Ro+H)=F=m*G*M/(Ro+H)^2=m*g*(Ro)^2/(Ro+H)^2
mw^2*(Ro+H)=m*g*(Ro)^2/(Ro+H)^2
w^2=g*(Ro)^2/(Ro+H)^3
w=корень(g*(Ro)^2/(Ro+H)^3)
T=2*pi/w=2*pi/корень(g*(Ro)^2/(Ro+H)^3)=2*pi*корень((Ro+H)^3/(g*(Ro)^2))
если Ro >> H
T=2*pi*корень((Ro+H)^3/(g*(Ro)^2))
2*pi*корень(Ro^3/(g*(Ro)^2)) =
= 2*pi*корень(Ro/g)
2*3,14*корень(6400000/9,81) сек
5072 сек
84,5 мин
1 час 25 минут
Упр8
1. Ракета-носитель массой 33 т приближаетсяк Международной космической станции массой 410 т. Определите силу притяжения
в момент, когда расстояние между их центрами масс уменьшилось до 100 м.
Космический корабль массой 8 т приблизился к орбитальной космической станции массой 20 т на расстояние 100 м. Найти силу их взаимного притяжения.
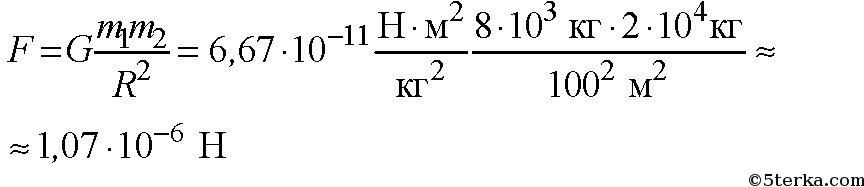
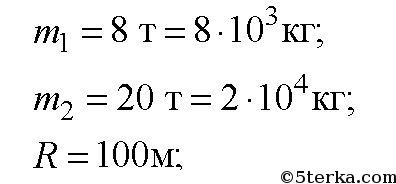
2. На каком расстоянии от поверхности Марса сила взаимодействия меж-
планетной станции Маринер-9 массой 1000 кг с планетой была равна
1,78 кН? Масса Марса равна 6,4 ∙ 10 23 кг, радиус 3400 км
В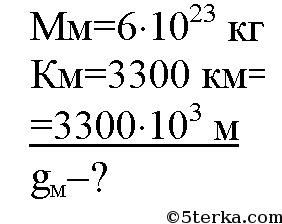 ычислите ускорение свободного падения тел вблизи поверхности Марса. Масса Марса равна 6⋅1023 кг, его радиус 3300 км.
ычислите ускорение свободного падения тел вблизи поверхности Марса. Масса Марса равна 6⋅1023 кг, его радиус 3300 км.
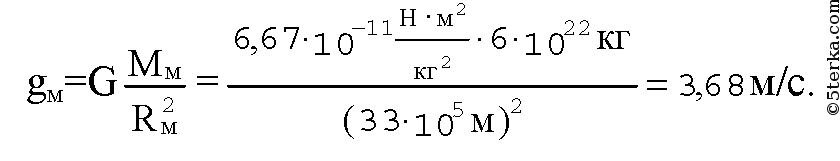
3. Среднее расстояние между центрами Земли и Луны равно 60 земным
радиусам, а масса Луны в 81 раз меньше массы Земли. В какой точке
прямой, соединяющей их центры, следует поместить тело, чтобы оно
притягивалось к Земле и Луне с одинаковыми силами?
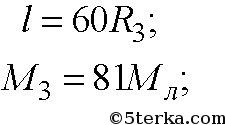
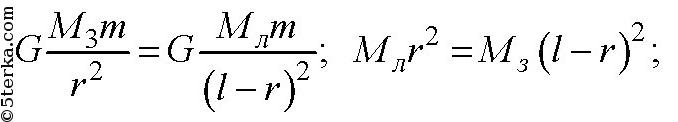
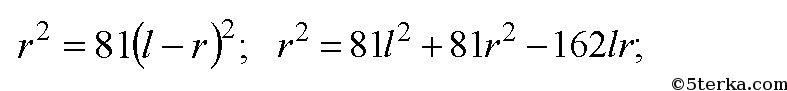
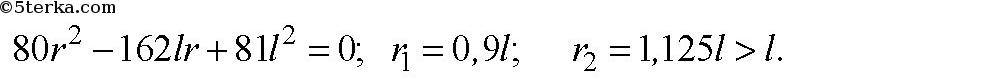
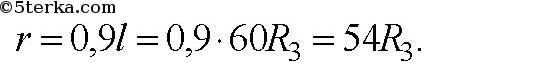
4. Определите силу притяжения шарика массой m и однородного шара,
внутри которого есть сферическая плоскость радиусом R/2 (рис. 32).
Радиус шара R, масса M, расстояние между центрами тяжести L
Масса шара, который заполнил бы сферическую полость, равна Mпол=(4/3)πρ(R/2)3=M/8Mпол=(4/3)πρ(R/2)3=M/8, а центр его лежит на расстоянии r−R/2r−R/2 от шарика массы mm. Искомая сила, равная разности сил притяжения сплошного шара и меньшего шара, заполняющего сферическую полость, выразится так: F=GMmr2−G(M/8)m(r−R/2)2=GMm[7r2−8rR+2R28r2(r−R/2)2]F=GMmr2−G(M/8)m(r−R/2)2=GMm[7r2−8rR+2R28r2(r−R/2)2].
6. Определите потенциал гравитационного поля на геостационарной орбите
Земли. Какой потенциальной энергией обладает космический аппарат
спутниковой связи РК KazSat-3 массой 1,3 тонны на этой орбите (рис. 34).
Расстояние от поверхности Земли до орбиты 36000 км. Масса Земли
6 ∙ 10 24 кг, радиус Земли 6400 км
определите кинетическую энергию космической станции при движении по орбите со скоростью 3,07 км/с, если масса станции 10 т.
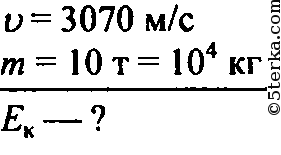
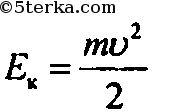
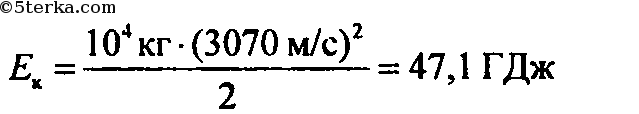
7. Спутник движется вокруг Земли на расстоянии H от ее поверхности.
Радиус Земли R 3 >> H. Определите период обращения спутника. Орбиту
считайте круговой
m*a=mw^2*(Ro+H)=F=m*G*M/(Ro+H)^2=m*g*(Ro)^2/(Ro+H)^2
mw^2*(Ro+H)=m*g*(Ro)^2/(Ro+H)^2
w^2=g*(Ro)^2/(Ro+H)^3
w=корень(g*(Ro)^2/(Ro+H)^3)
T=2*pi/w=2*pi/корень(g*(Ro)^2/(Ro+H)^3)=2*pi*корень((Ro+H)^3/(g*(Ro)^2))
если Ro >> H
T=2*pi*корень((Ro+H)^3/(g*(Ro)^2))
2*pi*корень(Ro^3/(g*(Ro)^2)) =
= 2*pi*корень(Ro/g)
2*3,14*корень(6400000/9,81) сек
5072 сек
Упр8
1. Ракета-носитель массой 33 т приближаетсяк Международной космической станции массой 410 т. Определите силу притяжения
в момент, когда расстояние между их центрами масс уменьшилось до 100 м.
Космический корабль массой 8 т приблизился к орбитальной космической станции массой 20 т на расстояние 100 м. Найти силу их взаимного притяжения.
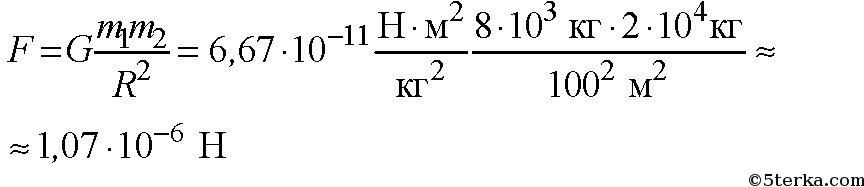
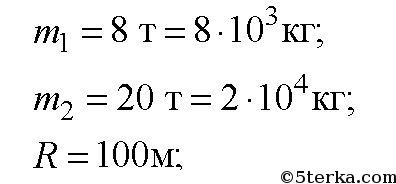
2. На каком расстоянии от поверхности Марса сила взаимодействия меж-
планетной станции Маринер-9 массой 1000 кг с планетой была равна
1,78 кН? Масса Марса равна 6,4 ∙ 10 23 кг, радиус 3400 км
В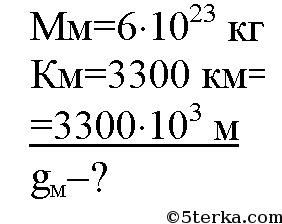 ычислите ускорение свободного падения тел вблизи поверхности Марса. Масса Марса равна 6⋅1023 кг, его радиус 3300 км.
ычислите ускорение свободного падения тел вблизи поверхности Марса. Масса Марса равна 6⋅1023 кг, его радиус 3300 км.
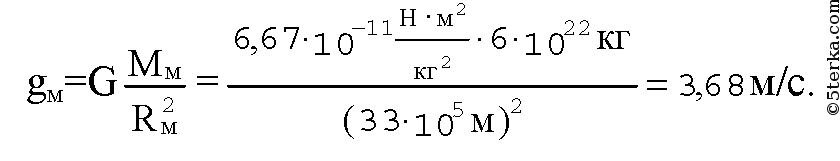
3. Среднее расстояние между центрами Земли и Луны равно 60 земным
радиусам, а масса Луны в 81 раз меньше массы Земли. В какой точке
прямой, соединяющей их центры, следует поместить тело, чтобы оно
притягивалось к Земле и Луне с одинаковыми силами?
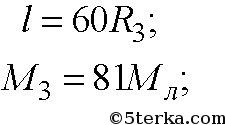
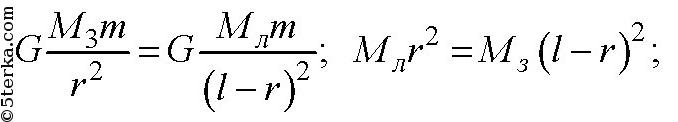
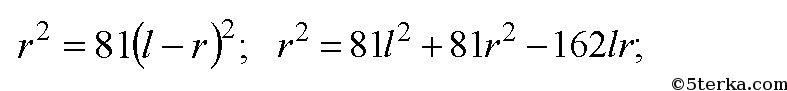
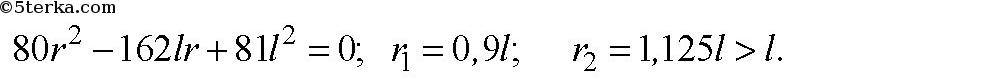
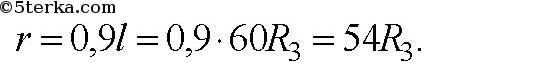
4. Определите силу притяжения шарика массой m и однородного шара,
внутри которого есть сферическая плоскость радиусом R/2 (рис. 32).
Радиус шара R, масса M, расстояние между центрами тяжести L
Масса шара, который заполнил бы сферическую полость, равна Mпол=(4/3)πρ(R/2)3=M/8Mпол=(4/3)πρ(R/2)3=M/8, а центр его лежит на расстоянии r−R/2r−R/2 от шарика массы mm. Искомая сила, равная разности сил притяжения сплошного шара и меньшего шара, заполняющего сферическую полость, выразится так: F=GMmr2−G(M/8)m(r−R/2)2=GMm[7r2−8rR+2R28r2(r−R/2)2]F=GMmr2−G(M/8)m(r−R/2)2=GMm[7r2−8rR+2R28r2(r−R/2)2].
6. Определите потенциал гравитационного поля на геостационарной орбите
Земли. Какой потенциальной энергией обладает космический аппарат
спутниковой связи РК KazSat-3 массой 1,3 тонны на этой орбите (рис. 34).
Расстояние от поверхности Земли до орбиты 36000 км. Масса Земли
6 ∙ 10 24 кг, радиус Земли 6400 км
определите кинетическую энергию космической станции при движении по орбите со скоростью 3,07 км/с, если масса станции 10 т.
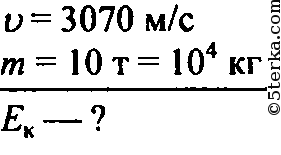
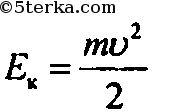
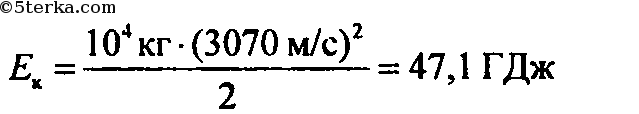
7. Спутник движется вокруг Земли на расстоянии H от ее поверхности.
Радиус Земли R 3 >> H. Определите период обращения спутника. Орбиту
считайте круговой
m*a=mw^2*(Ro+H)=F=m*G*M/(Ro+H)^2=m*g*(Ro)^2/(Ro+H)^2
mw^2*(Ro+H)=m*g*(Ro)^2/(Ro+H)^2
w^2=g*(Ro)^2/(Ro+H)^3
w=корень(g*(Ro)^2/(Ro+H)^3)
T=2*pi/w=2*pi/корень(g*(Ro)^2/(Ro+H)^3)=2*pi*корень((Ro+H)^3/(g*(Ro)^2))
если Ro >> H
T=2*pi*корень((Ro+H)^3/(g*(Ro)^2))
2*pi*корень(Ro^3/(g*(Ro)^2)) == 2*pi*корень(Ro/g)
упр9
1. Чему равен момент инерции для тела массой 200 г, вращающегося
по окружности радиусом 10 см, в момент, когда его скорость от нулевого
значения изменилась до значения 1,4 м/с? Определите среднее значение
угловой скорости.
Момент инерции (считаем тело точкой):
J = m*R²=0,2*0,1² = 0,002 кг*м²
Изменение момента импульса:
ΔL = J*Δω
Найдем изменение угловой скорости
ΔV = Δω*R
Δω=ΔV/R = 1,4/0,1= 14 c⁻¹
Тогда
ΔL = 0,002*14 = 0,028 кг*м/с²
2. Определите момент силы, приводящей автомобиль массой 2 т к ускорен-
ному движению по закругленному участку пути радиусом 20 м. Угловое
ускорение автомобиля 0,05 рад/с
Дано:
m = 2 т = 2000 кг
R = 0,02 км = 20 м
ε = 0,05 рад/с²
___________
M - ?
Момент силы:
M = J·ε
Считаем автомобиль материальной точкой. Тогда момент инерции автомобиля:
J = m·R²
Получаем:
M = J·ε = m·R²·ε
M = 2000·(20)²·0,05 = 40 000 Н·м или 40 кН·м
4. Диск массой 2 кг катится без проскальзывания по гори-
зонтальной плоскости со скоростью 4 м/с. Определите его
кинетическую энергию
Дано:
| m = 2 кг v = 4 м/с |
| Wк -? |
Упр 10
1. Определите момент импульса тела массой 0,1 кг, вращающегося по окруж-
ности радиусом 2 м в горизонтальной плоскости с угловой скоростью 2 π рад/с.
2. Определите момент силы, способной увеличить момент импульса тела
массой 0,1 кг, вращающегося по окружности радиусом 2 м в горизонтальной
плоскости с угловой скоростью 2 π рад/с, вдвое в течение одного оборота.
3. Определите момент силы, совершившей работу 3,14 Дж при перемещении
тела по окружности на φ = 30°

4. Две гири массой 0,2 кг и 0,1 кг соединены нитью и перекинуты через блок
массой 0,1 кг. Определите ускорение, с которым движутся гири, и натя-
жения нитей. Блок считать однородным диском. Трением пренебречь
a=g*(m2-m1)/(m2+m1)-ускорение грузов
из уравнения 1 системы получим T=m1g+m1a
из уравнения 2 получим T=m2g+m2a
T=2g*((m1*m2)/m2+m1))- сила натяжения нити!
m2-2 кг
m1-1 кг
g=10 м /с
считайте!
5. На барабан массой 9 кг намотан шнур, к концу которого привязан груз
массой 2 кг. Определите ускорение, с которым движется груз. Барабан
считать однородным цилиндром, трением пренебречь
Потенциальная энергия груза Ep = m · g · h, которая переходит в кинетическую энергию:
m · g · h = (m · v²) / 2 + (J · ω²) / 2
Момент инерции J = (m₀ · R²) / 2
Угловая скорость ω = ν / R
R - радиус барабана
m₀ - масса барабана
Подставляем в первое уравнение;
m · g · h = (m · v²) / 2 + (m₀ · v²) / 4
Заменим h через h = (a · t²) / 2 и v = a · t
Получим
a = (2 · m · g) / (m₀ + 2 · m) = (2 · 2 кг · 9,8 м/с²) / (9 кг + 2 · 2 кг) ≈ 3 м/с²
упр 11
1. Бревно длиной 12 м можно уравновесить в горизонтальном положении
на подставке, отстоящей на 3 м от его толстого конца. Если же подставка
находится в 6 м от толстого конца, и на тонкий конец сядет рабочий массой
60 кг, то бревно снова будет в равновесии. Определите массу бревна.
Дано:
L = 12 м
x = 3 м
R = 6 м
---------------
М - ?
бревном и человеком равны по модулю, поэтому если считать что человек сидит с самого края доски
Тогда
mgR = Mgh
mR = M( R - x )
M = ( mR )/( R - x )
M = ( 60 * 6 )/( 6 - 3 ) = 120 кг
2. К концам стержня массой 10 кг и длиной 40 см подвешены грузы массами
40 кг и 10 кг. Где необходимо подпереть стержень, чтобы он находился
в равновесии?
М = 10кг; I = 40см = 0,4м; m1 = 40кг; m2 = 10кг; х-?
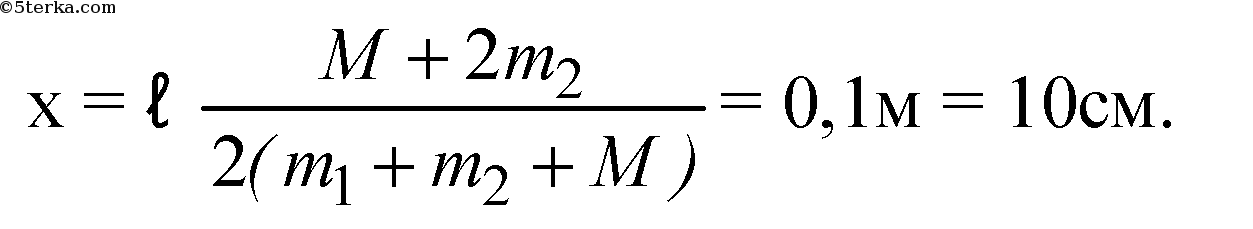
3. Одна половина цилиндрического стержня состоит из стали, другая –
из алюминия. Определить положение центра тяжести, если длина стержня
30 см.
Дано:
L=30 см;
ρ₁=7800 кг/м³;
ρ₂=2700 кг/м³;
____________
Найти:
Решение:
Обозначим площадь поперечного сечения за S, тогда массы половинок стержня: