Файл: Упр 1 Приведите примеры технических устройств, действие которых основано на открытии радиоактивности, электромагнитных волн, ультразвука, реактивного движения.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 10.11.2023

Просмотров: 137

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Упр81. Ракета-носитель массой 33 т приближаетсяк Международной космической станции массой 410 т. Определите силу притяженияв момент, когда расстояние между их центрами масс уменьшилось до 100 м.Космический корабль массой 8 т приблизился к орбитальной космической станции массой 20 т на расстояние 100 м. Найти силу их взаимного притяжения. 2. На каком расстоянии от поверхности Марса сила взаимодействия меж-планетной станции Маринер-9 массой 1000 кг с планетой была равна1,78 кН? Масса Марса равна 6,4 ∙ 10 23 кг, радиус 3400 кмВ ычислите ускорение свободного падения тел вблизи поверхности Марса. Масса Марса равна 6⋅1023 кг, его радиус 3300 км. 3. Среднее расстояние между центрами Земли и Луны равно 60 земнымрадиусам, а масса Луны в 81 раз меньше массы Земли. В какой точкепрямой, соединяющей их центры, следует поместить тело, чтобы онопритягивалось к Земле и Луне с одинаковыми силами? 4. Определите силу притяжения шарика массой m и однородного шара,внутри которого есть сферическая плоскость радиусом R/2 (рис. 32).Радиус шара R, масса M, расстояние между центрами тяжести LМасса шара, который заполнил бы сферическую полость, равна Mпол=(4/3)πρ(R/2)3=M/8Mпол=(4/3)πρ(R/2)3=M/8, а центр его лежит на расстоянии r−R/2r−R/2 от шарика массы mm. Искомая сила, равная разности сил притяжения сплошного шара и меньшего шара, заполняющего сферическую полость, выразится так: F=GMmr2−G(M/8)m(r−R/2)2=GMm[7r2−8rR+2R28r2(r−R/2)2]F=GMmr2−G(M/8)m(r−R/2)2=GMm[7r2−8rR+2R28r2(r−R/2)2]. 6. Определите потенциал гравитационного поля на геостационарной орбитеЗемли. Какой потенциальной энергией обладает космический аппаратспутниковой связи РК KazSat-3 массой 1,3 тонны на этой орбите (рис. 34).Расстояние от поверхности Земли до орбиты 36000 км. Масса Земли6 ∙ 10 24 кг, радиус Земли 6400 кмопределите кинетическую энергию космической станции при движении по орбите со скоростью 3,07 км/с, если масса станции 10 т. 7. Спутник движется вокруг Земли на расстоянии H от ее поверхности.Радиус Земли R 3 >> H. Определите период обращения спутника. Орбитусчитайте круговойm*a=mw^2*(Ro+H)=F=m*G*M/(Ro+H)^2=m*g*(Ro)^2/(Ro+H)^2mw^2*(Ro+H)=m*g*(Ro)^2/(Ro+H)^2w^2=g*(Ro)^2/(Ro+H)^3w=корень(g*(Ro)^2/(Ro+H)^3)T=2*pi/w=2*pi/корень(g*(Ro)^2/(Ro+H)^3)=2*pi*корень((Ro+H)^3/(g*(Ro)^2))если Ro >> HT=2*pi*корень((Ro+H)^3/(g*(Ro)^2)) 2*pi*корень(Ro^3/(g*(Ro)^2)) == 2*pi*корень(Ro/g) 2*3,14*корень(6400000/9,81) сек  5072 сек 84,5 мин

Ветер дует перпендикулярно стене. Плотность воздуха 1,29 кг/м 3p = 200 Паρ = 1,29 кг/м³_________v - ?F*Δt = 2*m*vm=ρ*V    (здесь V - объем, не путать с v - скоростью!!! :)F*Δt = 2*ρ*V*v              (1)Займемся объемом воздуха:V = S*L = S*v*Δt            (2) (S - площадь стены, L - путь, который воздух со  скоростью v пройдет за Δt секунд.Подставляя (2) в (1) получаем:F = 2*ρ*S*v²                   (3)Но сила давленияF = p*S                           (4)Опять приравниваем (4) и (3) и сокращаем на площадь стены:p = 2*ρ*v²Отсюда скорость:v = √ (p / (2·ρ) = √ (200 / (2·1,29) ≈ 8,5 м/с2. Определите силу давления ураганного ветра на стену дома высотой 30 ми длиной 50 м. Скорость ветра достигает 40 м/с и направлена под углом30° к стене. Сравните давление ветра с атмосферным давлением. Примитепоток воздуха вблизи стены ламинарным. упр 151. В широкой части горизонтальной трубы вода течет со скоростью 8 см/спри давлении, равном 1,5·10 5 Па. В узкой части трубы давление равно1,4·10 5 Па. Определите скорость течения в узкой части трубы без учетатрения.Для горизонтально расположенной трубы уравнение Бернулли записывается:rv1(2)/2+p1=rv2(2)/2+p2v2(2)=rv1(2)/2+p1-p2/(r/2)==1000кг/м3*(0.08м\с))*(0.08м\с)/2+1.5*10(5)Па-1.4*10(5)Па/1000кг\м3/2=4.47м\с2. В широкой части трубы нефть течет со скоростью 2 м/с. Определитескорость течения нефти в узкой части трубы, если разность давленийв широкой и узкой части трубы составляет 50 мм рт. СтУравнение: Р1+рgh1+рv1^2/2=Р2+рgh2+рv2^2/2. Здесь h1=h2, Р1-Р2=50мм. рт. ст. =

Определите внутреннюю энергию одноатом- ного идеального газа, взятого в количестве 5 молей, при температуре 27 °С? U = i/2*v*R*Ti=3 - для одноатомного газаv = 5 мольT=273+27=300 КU = i/2*v*R*T = 3/2 * 5 * 8,31 * 300 Дж = 18 698 Дж 18,7 КДж Зависит ли изменение внутренней энергии газа от способа его перевода из состояния 1 в состо- яние 2 (рис. 119)? Найдите изменение внутренней энергии при переходе из состояния 1 в состояние 2, если газ одноатомный; p0 = 105Па, V0 = 2 л. p1=3*10^4 Па V1=4 м3 р2=6*10^4 Па V2=12 м3 ΔU=?ΔU=(i/2)*v*R*ΔT Для 2-х атомных газов i=5Работа газа A=(p1+p2)*(V2-V1)/2=v*R*ΔT (графически - работа равна площади трапеции).ΔU=(5/4)*p1+p2)*(V2-V1)=(5/4)*(6+3)*(12-4)*10^4=0,9*10^6 Дж Один моль газа, имевший начальную температуру Т = 300 К, изобарно расширился, совершив работу А = 12,5·103 Дж. Во сколько раз при этом увеличится объем газа?

Плоский конденсатор с размером пластин 25 × 25 см и расстоянием между ними 0,5 мм заряжен от источника напряжения до разности потенциалов 10 В и отключен от источника. Какова будет разность потенциалов, если пластины конденсатора раздвинуть на расстояние 5 мм? Имеются три различных конденсатора. Электроемкость одного из них 2 мкФ. Когда все три конденсатора соединены последовательно, электро­ емкость соединения равна 1 мкФ. Когда конденсаторы соединены парал­ лельно, то электроемкость цепи 11 мкФ. Определите электроемкость двух неизвестных конденсаторов. Подставим численные значения: С2 = 3 Ф; С3 = 6 Ф или С2 = 6 Ф; С3 = 3 Ф. Электрическая схема, состоящая из двух последовательно соединенных незаряженных конденсаторов электроемкостью 1 мкФ и 3 мкФ, присоеди­ нена к источнику постоянного напряжения 220 В. Определите напряжение на каждом конденсаторе сразу после их подключения. Упр 35 Конденсатору емкостью 20 мкФ сообщили заряд 5 мкКл. Какова энергия заряженного конденсатора? Дано:C=20 мкФ;q=5 мкКл;_________Найти: WСИ: C=2*10⁻⁵ Ф; q=5*10⁻⁶ КлРешение:Воспользуемся формулой для энергии заряженного конденсатора: Выполним подстановку и расчет:  Дж или 625 нДжОтвет: 625 нДж. Электроемкость конденсатора, подключенного к источнику постоянного напряжения U = 1000 В, равна С1 = 5 пФ. Расстояние между его обклад­ ками уменьшили в n = 3 раза. Определите изменение заряда на обкладках конденсатора и энергии электрического поля. Согласно формуле (14.22) заряд конденсатора q = CU. Отсюда изменение заряда Δq — (С2 - C)U = (nC1 - C1)U = (п — 1)С1U = 10-8 Кл. Изменение энергии электрического поля Пластины воздушного конденсатора отсоединили от источника тока, раздвинули вдвое и заполнили зазор диэлектриком с диэлектрической проницаемостью, равной 4. Во сколько раз уменьшилась энергия электрического поля в конденсаторе? Конденсатор отсоединенФормула для энергииW= q^2/ 2CC1= e0S/d былоC2= 4e0S/2d= 2C1 сталоЕмкость увеличилась в 2 разаЭнергия уменьшилась в 2 разаОтвет уменьшилась в 2 раза Пластины плоского конденсатора, площадью 200 см² каждая, располо­ жены на расстоянии 1 см. Какова энергия поля, если его напряженность 500 кВ/м? Дано: Найти W.Решение. Ответ: W = 220 мкДж Конденсатору электроемкостью 2 мкФ сообщен заряд 10–3 Кл. Обкладки конденсатора соединили проводником. Определите количество теплоты, выделившееся в проводнике при разрядке конденсатора, и разность потенциалов между обкладками до и после разрядки. Упр 36 Через нить лампочки карманного фонаря за время t = 2 мин проходит  заряд q1 = 20 Кл. Определите силу тока и время, за которое через нить  лампочки пройдет заряд q2 = 60 Кл. Решение: I =  I = =   А Если за 2 мин проходит заряд q₁ = 20 Кл, то q₂ = 60 Кл пройдёт за 2 · 3 = 6 мин.  Чему равно удельное сопротивление ρ проводника, если при силе тока I = 1 А падение  напряжения на нем U = 1,2 B? Диаметр  проводника d = 0,5 мм, длина l = 47 мм. R=U/I=1,2/1=1,2 ОмR=p*L/sp=R*s/L   s=pi*D^2/4=3,14*0,25*10^-6/4=0,2*10^-6 м^2p=1,2*0,2*10^-6/4,5=5,3*10^-8 Ом*м Есть четыре резистора одинакового сопротивления R = 10 Ом. Сколько существует  способов их соединения? Определите эквивалентное сопротивление в каждом случае. Последовательное или параллельное соединение. При последовательном соединении их общее сопротивление будет равно 40 Ом. При параллельном соединении их общее сопротивление будет равно 2,5 Ом.Формулы для расчета: Последовательное соединение резисторов Rобщ =  R1 + R2 + R3 + R4Параллельное соединение резисторов 1/Rобщ = 1/R1 + 1/R2 + 1/R3 + 1/R4.  Определите общее сопротивление цепи, изображенной на рисунке 200, если R = 4 Ом.R1=6 ом, r2=12 om, r3=5 om, r4=4om, r5=2 om, r6=4 om.1/R1,2=1/6+1/12=1/4R1,2=4 Ом1/R4,5,6=1/4+1/2+1/4=1R4,5,6=1 ОмR=R1,2+R3+R4,5,6R=4+5+1=10 ОмОтвет: общее сопротивление 10 Ом.Упр 37 Конденсатор емкостью С = 100 мкФ, заряженный до напряжения U = 300 B  разряжается за время Δt = 0,1 с. Определите среднее значение силы тока  при разряде конденсатора. Uo=300 BC1=50 мкФC2=100 мкФ-------------Q2 - ?РЕШЕНИЕопределим начальный зарядQo=Uo*C1 = 300 *50*10^-6 =0.015 Клпри параллельном соединении емкость системы   C=C1+C2=50 мкФ+100 мкФ=150 мкФтогда общее напряжение  U=U1=U2=Qo/C=0.015 Кл / 150*10^-6 Ф =100 Взаряд на C1    Q1= U1*C1=100 *50*10^-6 =0.005 Клзаряд на С2    Q2= U2*C2=100 *100*10^-6 =0.01 Кл Конденсатор емкостью 100 мкФ заряжается до напряжения 500 B за 0,5 с.  Каково среднее значение силы зарядного тока? Батарея аккумуляторов состоит из n = 8 элементов, соединенных последовательно. ЭДС каждого из элементов ε = 1,5 В, внутреннее сопротивление  r = 0,25 Ом. Внешнюю цепь образуют два параллельно соединенных  проводника сопротивлениями R1 = 10 Ом и R2 = 50 Ом. Определите напряжение на зажимах батареи. Задачу решим по закону Ома для полной цепи:  I=E/(R+r)ЭДС складывается из всех источников E = e*8 = 1,5*8 = 12 в.Внутреннее сопротивление r = 0,25 * 8 = 2 омПри параллельном сопротивлении R = R1*R2/(R1+R2)= 50*10/(50+10)=25/3 = 8⅓ омI = 12/(2+8⅓) = 1,16 aU = I*R = 1,16*8⅓ = 9,7 в Две группы из трех последовательно соединенных элементов соединены  параллельно. ЭДС каждого элемента равна 1,2 В, внутреннее сопротивление r = 0,2 Ом. Полученная батарея замкнута на внешнее сопротивление R = 1,5 Ом. Определите силу тока во внешней цепи. Ответ:Даноэпсилон=U=1,2Br=0,2OmR=1,5Omнайти: I-?Решение R=R/(R+r)=1,5/1,7



 кг

 кг

Координаты центров масс каждой из половинок, будут совпадать с их серединами (см. рисунок). Координату общего центра масс легко найти по известной формуле:



Выполним подстановку и расчет:

 м
4. Расстояние между осями передних и задних колес автомобиля равно

2,3 м. При взвешивании автомобиля на весовой платформе выяснилось,

что нагрузка на передние колеса составляет 9 кН, а на задние – 6,5 кН

I = 2,3м; Р1 = 9кН; Р2 = 6,5кН; х -?



5. Определите координаты центра в мм масс однородных пластин, размеры

которых даны на рисунке 50.

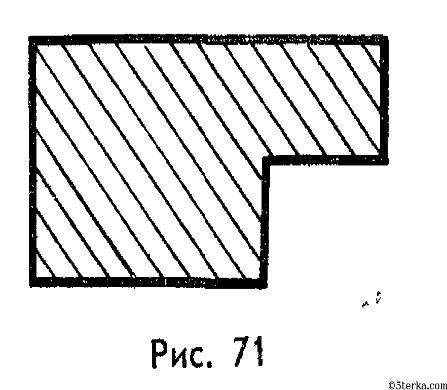Центр тяжести фигуры лежит на линии соединяющей центр тяжести

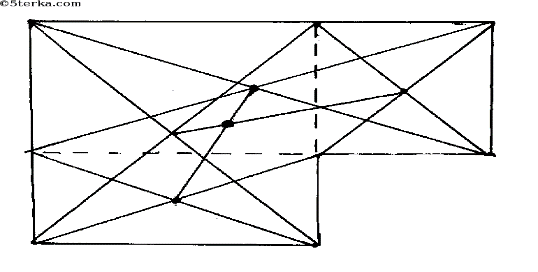прямоугольников. Разбивая на 2 прямоугольника 2-мя способами, найдем эту точку

Упр12

1. Определить виды равновесия в следующих

случаях: 1) бильярдный шар в лузе; 2) бусина

на горизонтально натянутой нити; 3) брусок

на наклонной плоскости; 4) гимнаст, идущий

по канату; 5) шарик в конической воронке; 6) лест-

ница, которую прислонили к стене; 7) коробка,

лежащая на полу

ответ:

устойчивое

безразличное

неустойчивое

неустойчивое

устойчивое

неустойчивое

безразличное
2. На доске стоит цилиндр высотой h и диаметром

d = h/2. Доску начинают медленно поднимать

за один конец. Что произойдет раньше: опроки-

нется ли цилиндр или начнет скользить? Коэф-

фициент трения между поверхностями цилиндра


и доски µ = 0,4.

Решение:







Упр 13

1,, Железнодорожный вагон массой 10 4 кг, движущийся со скоростью 25 м/с,сталкивается с неподвижным вагоном массой 1,5·10 4 кг. С какой скоро-

стью будут двигаться вагоны, если между ними сработает сцепка?

По закону сохранения импульса m1*V1=(m1+m2)*V
V=m1*V1/(m1+m2)=10^4*25/(10^4+1,5*10^4)=10 м/с

2. В модели ракеты общей массой 600 г содержится 350 г пороха. Выход

газов происходит мгновенно со скоростью 300 м/с. Сопротивление воз-

духа движению ракеты уменьшает высоту подъема в 6 раз. Определите

высоту подъема ракеты, примите g = 10 м/с 2

Дано m1=350 г   M=600 г   V1=300 м/с    h- ?

по закону сохранения импульса  0=m1*V1-m2*V2

V2=m1*V1/(M-m1)=300*350/250=420 м/с

по закону сохранения энергии m2*V2^2/2=m2*g*h

h=V2^2/2*g=420*420/20=8820 м
3. Два одинаковых абсолютно упругих шара движутся по гладкой горизон-

тальной поверхности навстречу друг к другу со скоростями 10 м/с и 5 м/с.

С какими скоростями и в каком направлении будут двигаться шары после

столкновения?
4. Пловец массой 70 кг прыгает в воду с вышки, находящейся на высоте 10 м

над поверхностью воды, и погружается на глубину 3 м. Выбрав поверх-

ность воды за нулевой уровень, определите потенциальную энергию

пловца на вышке и в момент максимального погружения.

mgh 70*10*10 = 7000 Дж 70*10*(-3) = -2100 Дж смысла во втором числе нет никакого, поскольку не учтена существенная сила - сила Архимеда, однако скорее всего от тебя требуется именно -2100

5. Спутник массой 1000 кг движется по круговой орбите вокруг Земли

на высоте 1000 км от ее поверхности. Определите потенциальную, кине-

тическую и полную энергии спутника.


Е(потенцияальная) =mgh h=1000000м.

E=1000*10*1000000=10 в 10 степени
6. Шар массой 0,02 кг, выпущенный из игрушечного пружинного пистолета,

летит вертикально вверх на высоту 57,6 см. Определите сжатие пружины,

жесткость которой равна 400 Н/м.

Дано:

m = 0,02 кг

h = 57,6 см = 0,576 м

k = 400 Н/м

_________

Δx - ?

Еп = m·g·h = 0,02·10·0,576 ≈ 0,115 Дж                          (1)

Энергия сжатой пружины:

Eпр = k·Δx²/2 = 400·Δx²/2 = 200·Δx²      Дж                (2)

Приравняем (2) и (1) по закону сохранения энергии:

200·Δx² = 0,115

Δx = √ (0,115/200) ≈ 0,024 м       или     24 мм
7. Определите вторую космическую скорость для нашей планеты

рхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния .



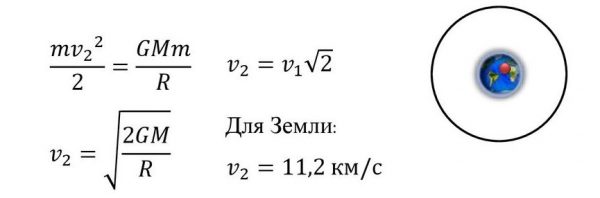
Упр 14

1. Определите скорость ветра, если он оказывает давление на стену 200 Па.


Ветер дует перпендикулярно стене. Плотность воздуха 1,29 кг/м 3

p = 200 Па
ρ = 1,29 кг/м³
_________
v - ?

F*Δt = 2*m*v
m=ρ*V    (здесь V - объем, не путать с v - скоростью!!! :)
F*Δt = 2*ρ*V*v              (1)
Займемся объемом воздуха:
V = S*L = S*v*Δt            (2)
 (S - площадь стены, L - путь, который воздух со  скоростью v пройдет за Δt секунд.
Подставляя (2) в (1) получаем:
F = 2*ρ*S*v²                   (3)
Но сила давления
F = p*S                           (4)
Опять приравниваем (4) и (3) и сокращаем на площадь стены:
p = 2*ρ*v²
Отсюда скорость:
v = √ (p / (2·ρ) = √ (200 / (2·1,29) ≈ 8,5 м/с

2. Определите силу давления ураганного ветра на стену дома высотой 30 м

и длиной 50 м. Скорость ветра достигает 40 м/с и направлена под углом

30° к стене. Сравните давление ветра с атмосферным давлением. Примите

поток воздуха вблизи стены ламинарным.


упр 15

1. В широкой части горизонтальной трубы вода течет со скоростью 8 см/с

при давлении, равном 1,5·10 5 Па. В узкой части трубы давление равно

1,4·10 5 Па. Определите скорость течения в узкой части трубы без учета

трения.

Для горизонтально расположенной трубы уравнение Бернулли записывается:

rv1(2)/2+p1=rv2(2)/2+p2

v2(2)=rv1(2)/2+p1-p2/(r/2)=

=1000кг/м3*(0.08м\с))*(0.08м\с)/2+1.5*10(5)Па-1.4*10(5)Па/1000кг\м3/2=4.47м\с
2. В широкой части трубы нефть течет со скоростью 2 м/с. Определите

скорость течения нефти в узкой части трубы, если разность давлений

в широкой и узкой части трубы составляет 50 мм рт. Ст

Уравнение: Р1+рgh1+рv1^2/2=Р2+рgh2+рv2^2/2. Здесь h1=h2, Р1-Р2=50мм. рт. ст. =

6666Па. Плотность нефти бывает разная, от 0,65 до 1,05. Примем 900кг/м3. v2=(2(Р1-Р2+рv1^2/2)/р) ^(1/2)=(2*(6666+900*2^2/2)/900)^(1/2)=4,34м/с. Конечно нужно еще учесть местные сопротивления (переход) , но думаю вам это не нужно.
3. По горизонтальной трубе переменного сечения течет вода. Площади попе-

речных сечений трубы в узкой и широкой ее части равны 10 см 2 и 20 см 2

соответственно. Разность давлений в указанных сечениях 200 мм водного

столба. Определите объем воды, проходящий через произвольное сечение

трубы за 1 с
шение:








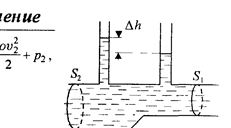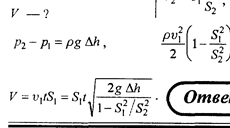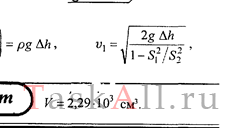4. Трубка расположена горизонтально. В широкой части трубы диаметром D

расположен поршень, на него действует постоянная сила F. Узкая часть

трубы имеет диаметр d, из нее вытекает струя воды. Определите скорость

перемещения поршня, трение не учитывайте

A = F v Δt. эта работа идет на приращение кинетической энергии столбиков воды:
F v Δt = (m/2) * (u² - v²)
диаметра d: S1 v Δt = S2 u Δt или v (π D²)/4 = u (π d²)/4, то есть
u = v (D/d)² (полученное выше равенство также называется теоремой о неразрывности струи) масса столбика воды: m = p V = p (π D²)/4 * v Δtобъединяя все полученные выше выражения, получаем:



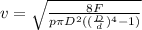
помимо прочего, можно решить несколько проще через закон Бернулли:
P1 + (p v²)/2 = P2 + (p u²)/2, где

P1 = (4 F)/(π D²) - давление, оказываемое на столбик воды поршнем
(p v²)/2 и (p u²)/2 - плотности кинетических энергий
P2 = 0, т.к. в трубе диаметра d на столбик воды давление не оказывается. считаем, что атмосферного давления нет

упр 16

1. На дне бака высотой 50 см, полностью заполненного водой, имеется

отверстие площадью 1 см 2 значительно меньшей площади сечения бака.

Если открыть отверстие, то из него начинает вытекать струя воды. Чему

равна площадь сечения струи на высоте 20 см ниже дна бака?

о закону сохранения энергии

m*g*h1=m*V1^2/2
V1=√2*g*h1

аналогично V2=√2*g*(h1+h2)
так как m1=m2  

Смотрите также файлы