Файл: Упр 1 Приведите примеры технических устройств, действие которых основано на открытии радиоактивности, электромагнитных волн, ультразвука, реактивного движения.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 136
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3. Какая работа совершается при переносе точечного заряда q = 2·10–8 Кл из бесконечности в точку, находящуюся на расстоянии d = 1 см от поверх ности шара радиусом r = 1 см с поверхностной плотностью заряда σ = 10–9 Кл/ см2?
Поэтапно:
1) Заряд шара q=сигма*S=сигма*4*pi*R^2=10^-9*4*3,14*1^2=12,56*10^-9 Кл
2) Потенциал, создаваемый шаром на расстоянии L от шара:
ф=k*q/(R+L)=9*10^9*12,56*10^-9/(0,01+0,01)=5652 В
3) В бесконечности потенциал равен 0. Тогда A=q1*ф=2*10^-8*5652=1,13*10^-4 Дж
Упр 32
-
Напряжение между двумя точками, лежащими на одной линии напряжен ности однородного поля, равно 2 кВ. Определите напряженность, если расстояние между точками 4 см.
Ответ:
U = 2 * 10^3 B
d = 0.04 м
E - ?
E = U/d = 5 В/м
-
Во сколько раз кулоновские силы отталкивания между двумя электронами больше силы гравитационного притяжения?


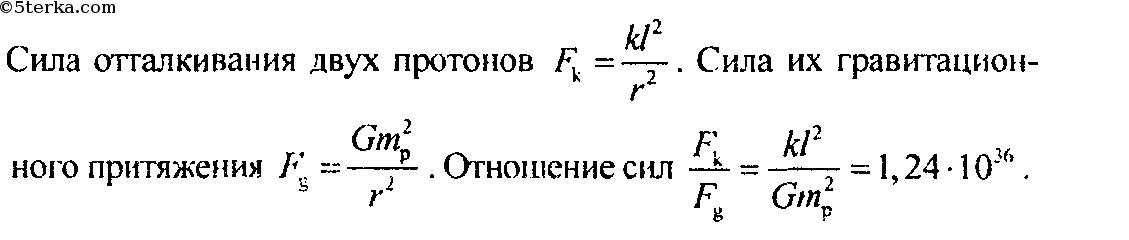
-
Заряд 5 нКл перемещен на 20 см в однородном электрическом поле напря женностью 60 кВ/м. Вектор перемещения образует угол 60° с направле нием силовой линии. Определите работу, совершенную полем, изменение потенциальной энергии заряда, напряжение между начальной и конечной точками перемещения.
Дано:
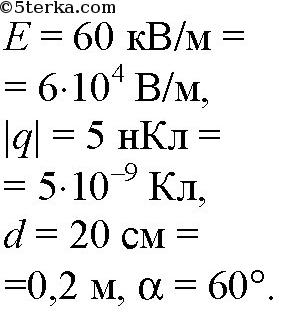
Найти A, ΔW, U.
Решение.
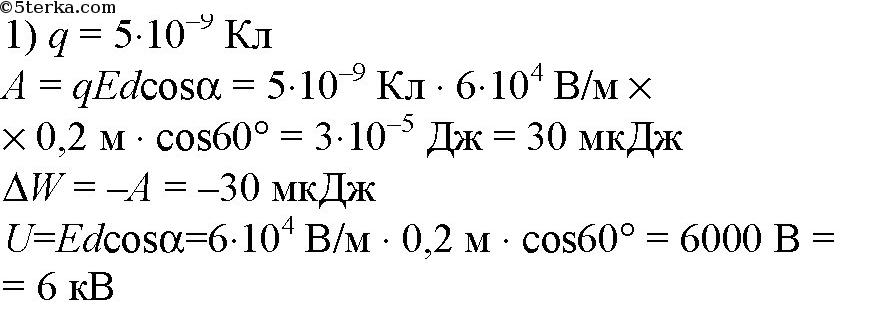
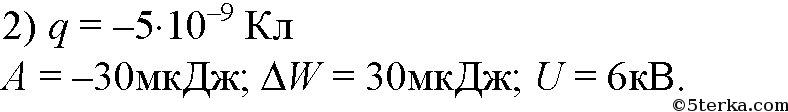
Ответ:
-
Три точечных заряда q1 = 2 нКл, q2 = 3 нКл и q3 = –4 нКл расположены в вершинах равностороннего треугольника со стороной a = 10 см. Опре делите потенциальную энергию этой системы.
Дано:
q₁=2нкл= кл
q₂=3нкл= кл
q₃=-4нкл= кл
a=10 см=0,1 м
Решение:
Упр 33
1. Одной из двух параллельных металлических пластин, которые расположенных на небольшом расстоянии друг от друга, сообщают заряд q = 4 нКл. Какие заряды будут индуцированы на каждой стороне другой пластины? Какова напряженность поля между пластинами?
2. Определите изменение силы взаимодей ствия двух шаров, центры которых нахо дятся на расстоянии l, после того как их соединят тонкой проволокой (рис. 183). Заряды шаров равны q1 и q2 = 2 q1, радиусы шаров равны r1 и r2 = 2r1.
при электрическом контакте двух заряженных шаров суммарный заряд q1+q2 перераспределяется таким образом чтобы потенциал на шариках был одинаков
пусть q1;q2 - исходные заряды шаров
Q1;Q2 - конечные заряды шаров
q1+q2 =Q1+Q2
U=1/(4*pi*e0)*Q1/R1=1/(4*pi*e0)*Q2/R2 - установившийся общий потенциал
Q1/R1=Q2/R2
Q1=(q1+q2)*R1/(R1+R2)
Q2=(q1+q2)*R2/(R1+R2)
U=1/(4*pi*e0)*Q1/R1=1/(4*pi*e0)*(q1+q2)/(R1+R2) - это ответ
-
С какой силой взаимодействуют два точечных заряда q1 = 6,6 мкКл и q2 = 1,2 мкКл в керосине на расстоянии R = 10 см друг от друга? На каком расстоянии их следует поместить в вакууме, чтобы сила взаимодействия осталась прежней?
диэлектрическая проницаемость воды
F=
-
Заряженный шарик погрузили в масло. На каком расстоянии от шарика напряженность поля будет такой же, какой была до погружения на расстоянии R = 29 см.
Дано:
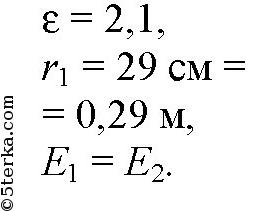
Найти r2.
Решение.
Решение.
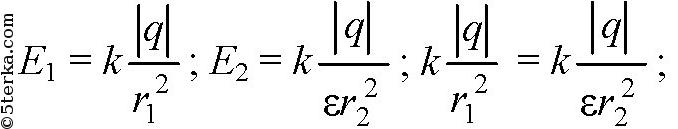
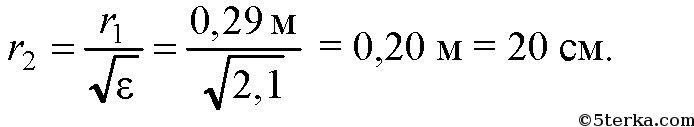
Ответ: r2 = 20 см.
-
Две большие пластины расположены горизонтально на небольшом рассто янии друг от друга. На нижней непроводящей пластине лежит маленький шарик с зарядом q = 20 мкКл. На сколько изменится вес шарика, если пространство между пластинами заполнить жидкостью плотностью ρ = 800 кг/м3 с диэлектрической проницаемостью ε? Объем шарика V = 1 см3, напряженность электрического поля, созданного верхней поло жительно заряженной пластиной, Е = 100 В/м.

Упр 34
-
Конденсатор, состоящий из двух пластин, имеет электроемкость 5 пФ. Какой заряд находится на каждой из его обкладок, если разность потенци алов между ними 1000 В?
- 1 2 3 4 5 6 7 8
Плоский конденсатор с размером пластин 25 × 25 см и расстоянием между ними 0,5 мм заряжен от источника напряжения до разности потенциалов 10 В и отключен от источника. Какова будет разность потенциалов, если пластины конденсатора раздвинуть на расстояние 5 мм?
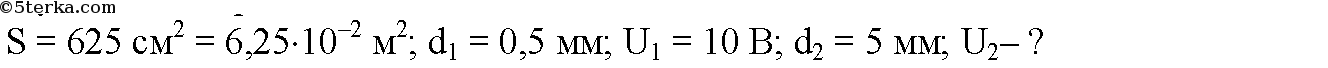
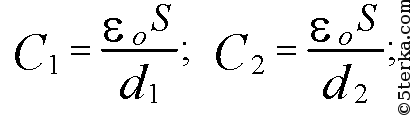
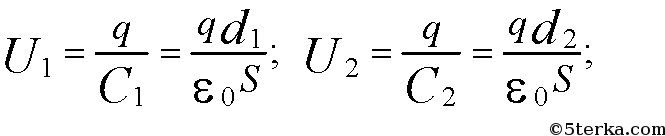
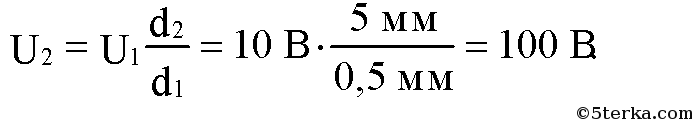
-
Имеются три различных конденсатора. Электроемкость одного из них 2 мкФ. Когда все три конденсатора соединены последовательно, электро емкость соединения равна 1 мкФ. Когда конденсаторы соединены парал лельно, то электроемкость цепи 11 мкФ. Определите электроемкость двух неизвестных конденсаторов.
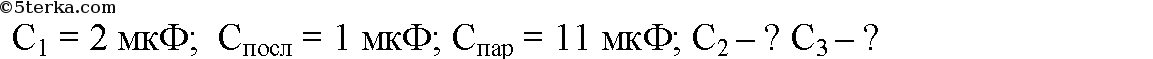
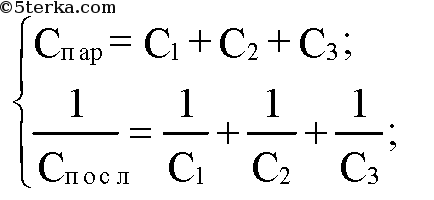
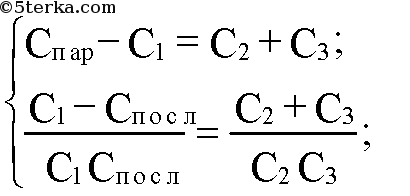
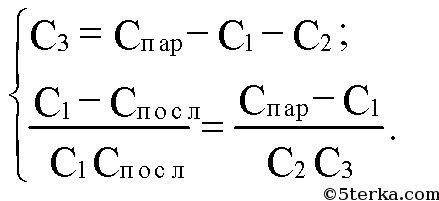
Подставим численные значения:
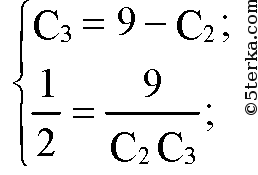
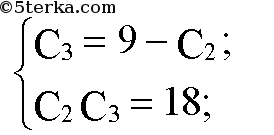
С2 = 3 Ф; С3 = 6 Ф или С2 = 6 Ф; С3 = 3 Ф.
-
Электрическая схема, состоящая из двух последовательно соединенных незаряженных конденсаторов электроемкостью 1 мкФ и 3 мкФ, присоеди нена к источнику постоянного напряжения 220 В. Определите напряжение на каждом конденсаторе сразу после их подключения.
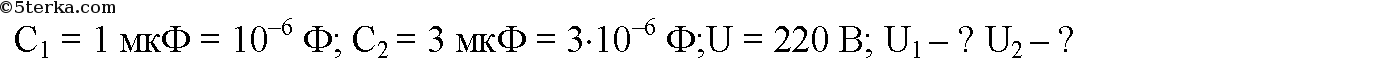
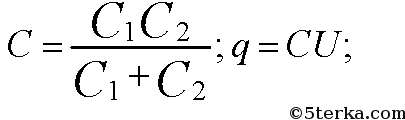
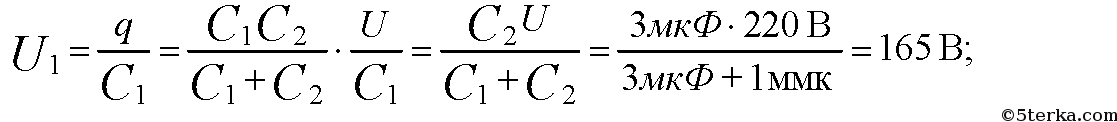
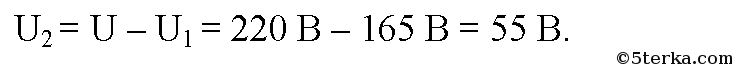
Упр 35
-
Конденсатору емкостью 20 мкФ сообщили заряд 5 мкКл. Какова энергия заряженного конденсатора?
Дано:
C=20 мкФ;
q=5 мкКл;
_________
Найти: W
СИ: C=2*10⁻⁵ Ф; q=5*10⁻⁶ Кл
Решение:
Воспользуемся формулой для энергии заряженного конденсатора:
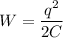
Выполним подстановку и расчет:
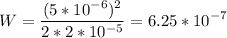 Дж или 625 нДж
Дж или 625 нДж
Ответ: 625 нДж.
-
Электроемкость конденсатора, подключенного к источнику постоянного напряжения U = 1000 В, равна С1 = 5 пФ. Расстояние между его обклад ками уменьшили в n = 3 раза. Определите изменение заряда на обкладках конденсатора и энергии электрического поля.
Согласно формуле (14.22) заряд конденсатора q = CU. Отсюда изменение заряда Δq — (С2 - C)U = (nC1 - C1)U = (п — 1)С1U = 10-8 Кл.
Изменение энергии электрического поля
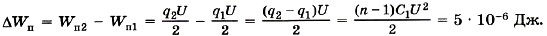
-
Пластины воздушного конденсатора отсоединили от источника тока, раздвинули вдвое и заполнили зазор диэлектриком с диэлектрической проницаемостью, равной 4. Во сколько раз уменьшилась энергия электрического поля в конденсаторе?
Конденсатор отсоединен
Формула для энергии
W= q^2/ 2C
C1= e0S/d было
C2= 4e0S/2d= 2C1 стало
Емкость увеличилась в 2 раза
Энергия уменьшилась в 2 раза
Ответ уменьшилась в 2 раза
-
Пластины плоского конденсатора, площадью 200 см² каждая, располо жены на расстоянии 1 см. Какова энергия поля, если его напряженность 500 кВ/м?
Дано: 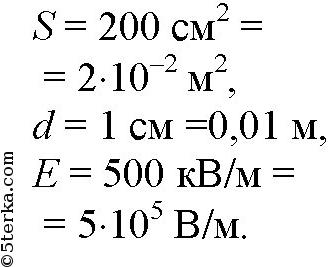
Найти W.
Решение.
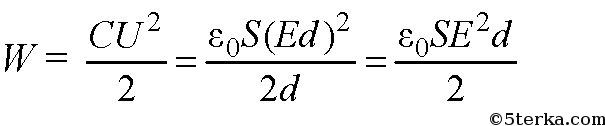
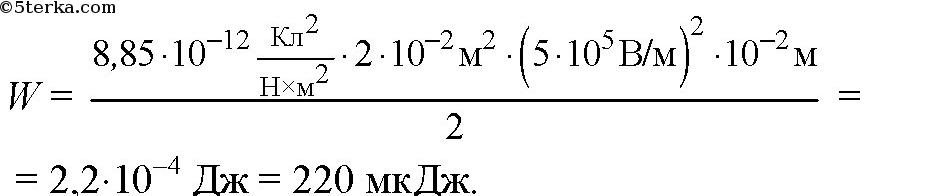
Ответ: W = 220 мкДж
-
Конденсатору электроемкостью 2 мкФ сообщен заряд 10–3 Кл. Обкладки конденсатора соединили проводником. Определите количество теплоты, выделившееся в проводнике при разрядке конденсатора, и разность потенциалов между обкладками до и после разрядки.
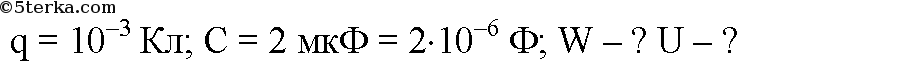
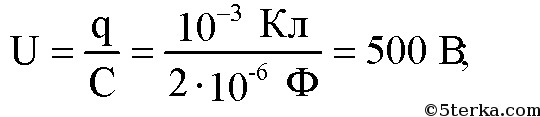
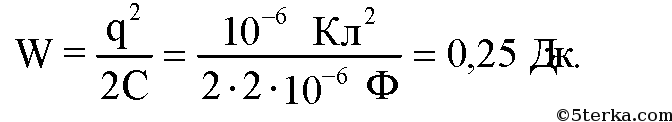
Упр 36
-
Через нить лампочки карманного фонаря за время t = 2 мин проходит заряд q1 = 20 Кл. Определите силу тока и время, за которое через нить лампочки пройдет заряд q2 = 60 Кл.
Решение: I =
I = = А Если за 2 мин проходит заряд q₁ = 20 Кл, то q₂ = 60 Кл пройдёт за 2 · 3 = 6 мин.
-
Чему равно удельное сопротивление ρ проводника, если при силе тока I = 1 А падение напряжения на нем U = 1,2 B? Диаметр проводника d = 0,5 мм, длина l = 47 мм.
R=U/I=1,2/1=1,2 Ом
R=p*L/s
p=R*s/L s=pi*D^2/4=3,14*0,25*10^-6/4=0,2*10^-6 м^2
p=1,2*0,2*10^-6/4,5=5,3*10^-8 Ом*м
-
Есть четыре резистора одинакового сопротивления R = 10 Ом. Сколько существует способов их соединения? Определите эквивалентное сопротивление в каждом случае.
Последовательное или параллельное соединение. При последовательном соединении их общее сопротивление будет равно 40 Ом. При параллельном соединении их общее сопротивление будет равно 2,5 Ом.
Формулы для расчета:
Последовательное соединение резисторов Rобщ = R1 + R2 + R3 + R4
Параллельное соединение резисторов 1/Rобщ = 1/R1 + 1/R2 + 1/R3 + 1/R
4. Определите общее сопротивление цепи, изображенной на рисунке 200, если R = 4 Ом.
R1=6 ом, r2=12 om, r3=5 om, r4=4om, r5=2 om, r6=4 om.
1/R1,2=1/6+1/12=1/4
R1,2=4 Ом
1/R4,5,6=1/4+1/2+1/4=1
R4,5,6=1 Ом
R=R1,2+R3+R4,5,6
R=4+5+1=10 Ом
Ответ: общее сопротивление 10 Ом.
Упр 37
-
Конденсатор емкостью С = 100 мкФ, заряженный до напряжения U = 300 B разряжается за время Δt = 0,1 с. Определите среднее значение силы тока при разряде конденсатора.
Uo=300 B
C1=50 мкФ
C2=100 мкФ
-------------
Q2 - ?
РЕШЕНИЕ
определим начальный заряд
Qo=Uo*C1 = 300 *50*10^-6 =0.015 Кл
при параллельном соединении емкость системы C=C1+C2=50 мкФ+100 мкФ=150 мкФ
тогда общее напряжение U=U1=U2=Qo/C=0.015 Кл / 150*10^-6 Ф =100 В
заряд на C1 Q1= U1*C1=100 *50*10^-6 =0.005 Кл
заряд на С2 Q2= U2*C2=100 *100*10^-6 =0.01 Кл
-
Конденсатор емкостью 100 мкФ заряжается до напряжения 500 B за 0,5 с. Каково среднее значение силы зарядного тока?

-
Батарея аккумуляторов состоит из n = 8 элементов, соединенных последовательно. ЭДС каждого из элементов ε = 1,5 В, внутреннее сопротивление r = 0,25 Ом. Внешнюю цепь образуют два параллельно соединенных проводника сопротивлениями R1 = 10 Ом и R2 = 50 Ом. Определите напряжение на зажимах батареи.
Задачу решим по закону Ома для полной цепи: I=E/(R+r)
ЭДС складывается из всех источников E = e*8 = 1,5*8 = 12 в.
Внутреннее сопротивление r = 0,25 * 8 = 2 ом
При параллельном сопротивлении R = R1*R2/(R1+R2)= 50*10/(50+10)=25/3 = 8⅓ ом
I = 12/(2+8⅓) = 1,16 a
U = I*R = 1,16*8⅓ = 9,7 в
-
Две группы из трех последовательно соединенных элементов соединены параллельно. ЭДС каждого элемента равна 1,2 В, внутреннее сопротивление r = 0,2 Ом. Полученная батарея замкнута на внешнее сопротивление R = 1,5 Ом. Определите силу тока во внешней цепи.
Ответ:Дано
эпсилон=U=1,2B
r=0,2Om
R=1,5Om
найти: I-?
Решение R=R/(R+r)=1,5/1,7
0,9Om
Имеются три различных конденсатора. Электроемкость одного из них 2 мкФ. Когда все три конденсатора соединены последовательно, электро емкость соединения равна 1 мкФ. Когда конденсаторы соединены парал лельно, то электроемкость цепи 11 мкФ. Определите электроемкость двух неизвестных конденсаторов.
Электрическая схема, состоящая из двух последовательно соединенных незаряженных конденсаторов электроемкостью 1 мкФ и 3 мкФ, присоеди нена к источнику постоянного напряжения 220 В. Определите напряжение на каждом конденсаторе сразу после их подключения.
Конденсатору емкостью 20 мкФ сообщили заряд 5 мкКл. Какова энергия заряженного конденсатора?
Электроемкость конденсатора, подключенного к источнику постоянного напряжения U = 1000 В, равна С1 = 5 пФ. Расстояние между его обклад ками уменьшили в n = 3 раза. Определите изменение заряда на обкладках конденсатора и энергии электрического поля.
Пластины воздушного конденсатора отсоединили от источника тока, раздвинули вдвое и заполнили зазор диэлектриком с диэлектрической проницаемостью, равной 4. Во сколько раз уменьшилась энергия электрического поля в конденсаторе?
Пластины плоского конденсатора, площадью 200 см² каждая, располо жены на расстоянии 1 см. Какова энергия поля, если его напряженность 500 кВ/м?
Конденсатору электроемкостью 2 мкФ сообщен заряд 10–3 Кл. Обкладки конденсатора соединили проводником. Определите количество теплоты, выделившееся в проводнике при разрядке конденсатора, и разность потенциалов между обкладками до и после разрядки.
Через нить лампочки карманного фонаря за время t = 2 мин проходит заряд q1 = 20 Кл. Определите силу тока и время, за которое через нить лампочки пройдет заряд q2 = 60 Кл.
Чему равно удельное сопротивление ρ проводника, если при силе тока I = 1 А падение напряжения на нем U = 1,2 B? Диаметр проводника d = 0,5 мм, длина l = 47 мм.
Есть четыре резистора одинакового сопротивления R = 10 Ом. Сколько существует способов их соединения? Определите эквивалентное сопротивление в каждом случае.
Конденсатор емкостью С = 100 мкФ, заряженный до напряжения U = 300 B разряжается за время Δt = 0,1 с. Определите среднее значение силы тока при разряде конденсатора.
Конденсатор емкостью 100 мкФ заряжается до напряжения 500 B за 0,5 с. Каково среднее значение силы зарядного тока?
Батарея аккумуляторов состоит из n = 8 элементов, соединенных последовательно. ЭДС каждого из элементов ε = 1,5 В, внутреннее сопротивление r = 0,25 Ом. Внешнюю цепь образуют два параллельно соединенных проводника сопротивлениями R1 = 10 Ом и R2 = 50 Ом. Определите напряжение на зажимах батареи.
Две группы из трех последовательно соединенных элементов соединены параллельно. ЭДС каждого элемента равна 1,2 В, внутреннее сопротивление r = 0,2 Ом. Полученная батарея замкнута на внешнее сопротивление R = 1,5 Ом. Определите силу тока во внешней цепи.
I=U/R=1,2/0,9=1,3А
Упр 38
-
В проводнике сопротивлением R = 2 Ом, подключенном к источнику тока с ЭДС ε = 1,1 В, сила тока I = 0,5 А. Определите силу тока при коротком замыкании источника.
Дано: R=2 Ом, ε=1,1 В, I = 0,5A Найти I3.
Решение.
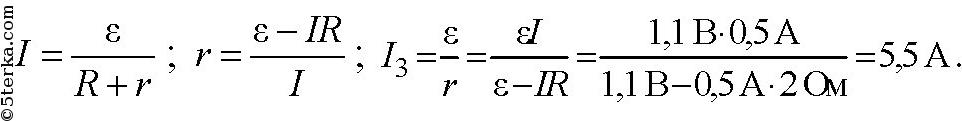
Ответ: I3 = 5,5 А.
-
Сила тока в цепи, содержащей источник тока и сопротивление R1 = 4 Ом, равна I1 = 0,2 А. Если внешнее сопротивление R2 = 7 Ом, то сила тока в цепи I2 = 0,14 А. Чему будет равна сила тока в цепи, если источник зам- кнуть накоротко?
R1=4 Ом I1=0.2 A R2=7 Ом I2=0.14 A Iкз=?
===
I1*(R1+r)=I2*(R2+r) (ЭДС в обоих случаях не меняется)
r=(I2*R2-I1*R1)/(I1-I2)=(0.14*7-0.2*4)/(0.2-0.14)=3 Ом
E=I1*(R1+r)=0.2*(4+3)=1.4 B
Iкз=E/r=1.4/3=0.47 A
-
При силе тока I1 = 1,5 А напряжение на участке цепи U1 = 20 В, а при силе тока I2 = 0,5 А напряжение на том же участке U2 = 8 В. Чему равна ЭДС, действующая на этом участке?
Закон Ома для полной цепи
I1=E/(R1+r)
I2=E/(R2+r)
найдем r- внутреннее сопротивление источника
E=I1R1+I1r I1R1=U1 E-U1+I1r E-U1=I1r r=(E-U1)/I1
r=(E-U2)/I2
(E-U1/I1)=(E-U2)/I2 E=(U1I2-U2I1)/(I2-I1)=2 В
-
К аккумулятору с внутренним сопротивлением 2 Ом и ЭДС 12 В под- ключены две одинаковые параллельно соединенные лампочки. Сила тока в одной из лампочек равна 1 А. Определите силу тока через эту лампочку, если другая перегорит.
Ответ:
1.2 Ампера
Объяснение:
r = 2 Ом
E = 12 В
I = 1 А
I3=?
Найдем сопротивление всей цепи (две лампы)
Общий ток (лампы одинаковы)
I=I1+I2=1+1=2A
E/I=R+r
12/(2) = R+2