№ 1 Зертханалық жұмыс

MatLab ортасында сандарды ондық және екілік санау жүйесіне айналдыру алгоритмін жүзеге асыру

Жұмыстың мақсаты: Берілген алгоритм бойынша MatLab ортасында сандарды әртүрлі санау жүйесіне автоматты түрлендіруді үйрену және алгоритм блок сұлбасы мен танысу

Қысқаша теориялық кіріспе

Санау жүйесі - цифрлық белгілер арқылы сандарды жазу заңдылығы.

Сан - мөлшер шамасын сипаттайтын абстрактілік мазмұны.

Цифр - сандарды жазу үшін қолданылатын белгілер.

Сандар цифрларға қарағанда көп болғандықтан, сандарды жазу үшін көп жағдайда цифрлар жиынтығы қолданылады. Сандардың аз мәнін жазу үшін - көлемі бойынша аз мәндерді жазу үшін бір цифр жеткілікті болады.

Цифр арқылы сандарды жазу үшін көптеген тәсілдер бар,оларды санау жүйесі деп атайды. Сандардың көлемін жазған кезде ол цифр ретіне тәуелді болуы мүмкін.

р символындағы Х алфавиті және жазу заңдылығы, сондай-ақ осы алфавит арқылы сандарды өңдеу р негізіндегі санау

жүйесі деп аталынады. Х саныр негізіндегі жүйеде Хр деп жазылады. Жүйенің негізі санның оң жағында, төменде индекс ретінде жазылады: 5₁₀, 1110011001₂, AB196₁₆, және т. б.

Санау жүйесінің негізі деп санды көрсету үшін қолданылатын цифрлар мен символдардың санын айтады. Мысалы, 0, 1,2, 3, 4, 5, 6, 7, 8, 9 қолданылады. Олар 10-ға тең, сондықтан біздің санау жүйеміздің негізі 10 болады және санау жүйесі «он-дық» деп аталады.

Жүйенің базасы - санды жазу үшін қолданылатын цифрлардың реті. Жүйеде жүйенің негізіне тең болатын цифр болмайды.

Кез келген санау жүйесі - сандық көлемді кодтау жүйесі болып табылады, олар кодтауды және декодтау ды орындайды, яғни кез келген сан көлемі бойынша кодты жазылуын табады және кез келген кодты жазба арқылы сәйкесінше сандық мәнін қайта жазады.

Информатикада көп қолданылатын санау жүйелері төменде көретілген:

-екілік: алфавиттің төменгі жағында жазылады, Х- {0, 1}

- сегіздік: алфавиттің төменгі жағында жазылады, Х- {0, 1,2, 3, 4, 5, 6, 7};

-он алтылық: алфавиттің төменгі жағында жазылады,X{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F1, A, B, C, D, E, F} символдары 10, 11, 12, 13, 14, 15 сандық мөлшерге сәйкес келеді.

Барлық санау жүйелері жалпы принцип бойынша құрылады: p - жүйенің негізін анықтайды, ал кез келген х сан 0-ден n-ге дейінгі дәрежеде p көлемнің дәреже амалы түрінде жазылады,

ол келесі түрде болады:

---

( x)_{Р =} X_np^n-1 + X_n-1P^n-2 +… + X₂P¹ + X₁P⁰ .

Бір санау жүйесінен басқа санау жүйесіне түрлендіру заңдылықтары

Бір жүйеден басқа санау жүйесіне түрлендіру - машиналык арифметиканың үлкен бөлімі. Тұрлендірудің негізгі тұрлерін қарастырайық.

1. Екілік жүйені ондық санау жүйесіне түрлендіру үшін оны көпмүше түрінде жазып, ондық арифметика заны бойынша есептеп шығу қажет:

X₂ = A_n * 2^n-1 + A_n-1 * 2^n-2 + A_n-2 *2^n-3 +… + A_{2 *} 2¹ + A₁ *2⁰ .

Түрлендіру кезінде екілік дәреже кестесін қолданған қолайлы ;

1. 1-кесте

2 санының дәрежесі

n ( дәреже)	0	1	2	3	4	5	6	7	8	9	10
2n	1	2	4	8	16	32	64	128	256	512	1024

2. Сегіздік санау жүйесін ондық санау жүйесіне аудару үшін 8 санының ләрежесіне сәйкес келетін және сандарды көбейту цифрынан тұратын көпмүше түрінде жазып шығу қажет, сондай-ақ ондық арифметика арқылы есептеу келесі түрде болады :

X₈ =A_n 8^n-1 + A^n-1p^n-2 + …. + A₂p¹ + A₁p⁰ .

1.2- кесте

8 санының дәрежесі

n (дәреже)	0	1	2	3	4	5	6
8n	1	8	64	512	4096	32768	262144

3. Он алтылық санау жүйесін ондық санау жүйесіне аудару үшін 16 санының дәрежесіне сәйкес келетін және сандарды көбейту цифрынан тұратын көпмүше түрінде жазып шығу қажет, сондай- ақ ондық арифметика арқылы есептеу׃

x₁₆ = A_n 16^n-1 + A_n-1 16^n-2 +… + A₂ 16¹ + A₁16⁰.

Есептеу кезінде сегіздік дәреже кестесін қолданған қолайлы:

---

1.3 - кесте

16 санының дәрежесі

n дәреже	0	1	2	3	4	5	6
16n	1	16	256	4096	65536	1048576	16777216

4. Ондық санды екілік жүйеге аудару үшін оны кезекпен немесе аз болады. Екілік жүйеде сан қалдықтан бастап белінген нәтиже ретімен жазылады.

5. Ондык санды сегіздік санау жүйесіне аудару үшін оны кезекпен калдық қалмағанша 8-ге беліп отыру қажет, қалдық 7-ге тең немесе 7-ден аз болады. Сегіздік жүйеде сан қалдықтан бастап бөлінген нәтиже ретімен жазылады.

6. Ондық санды он алтылық жүйеге аудару үшін оны кезекпен қалдық қалмағанша 16-ға бөліп отыру кажет, қалдық 16-ға тең немесе аз болады. Он алтылық жүйеде сан калдықтан бастап белінген нәтиже ретімен жазылады.

7. Екілік санау жүйесінен сегіздік санау жүйесіне аудару үшін әрбір санды триада бөліп, содан кейің сегіздік санау жүйесінде сәйкес келетін цифрлар жазылады.

8. Сегіздік санау жүйесін екілікке аудару үшің әрбір цифрды оған сәйкес келетін екілік триад түрінде жазады.

1-мысал. 22₁₀ ондық санау жүйесін екілікке аудару қажет:



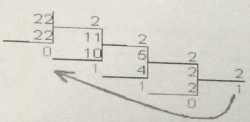
Жауабы: 22₁₀ = 10110₂.

Көрсетілген мысал бойынша MatLab ортасында бағдарлама жазу үшін, біріншіден, автоматты блок-сұлбасын құру қажет.

Блок-сұлба - алгоритмді немесе үрдісті бейнелейтін сұлба (графикалық модель) түрі, онда эрбір жеке кадам әртүрлі блокт түрінде көрсетіледі, олар өзара сызықтармен жалғастырылады, сызыктар реттің бағытын көрсетеді.

Алгоритм сұлбасының негізгі элементтері:

1. Алгоритмнің басы мен соны - бағдарламаның басы мен санын көрсетеді. Белгіленуі төменде көрсетілген.



2. Алгоритмнің үрдісі - есептеу барысын немесе үрдістің ретін көрсетеді. Белгіленуі төмендегідей болады:



3. Есепке шарт қою - шартты қолдану аркылы есепті тексеру.



4. Алдын ала белгіленген үрдіс - бағдарламаның жүйесін есептеу.



5. Енгізу- шығару функциясы - алгориигмге кажетті айнымалыларды енгізу үшін немесе шығару үшін қолданылады.

---

6. Модификация - шарт пен циклды бірге керсетеді.



7. Нәтижесін шығару блогы.



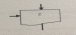
2-мысал. Қандай да бір санды 2-ге көбейткенде, шыққан біріншіден, есептің шешімі болатындай блок-сұлбасын құрастырамыз.



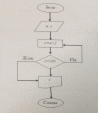
1.1- сурет. Блок - сұлба

Ендігі кезекте осы блок-сұлба үшін MatLab бағдарламасында бағдарлама жазылады:

>> a = 1

while c < 100;

C = a * 2;

end

>>a.

Яғни бағдарламаның соңында 100-ден кіші сандар есептің жауабы ретінде қабылданады.

Зертханалықжұмыстң орындауреті:

1. 1.5-кестеде берілген нұсқа бойынша берілген санау жүйесіне кілік санау жүйесіне түрлендіріңіз.

2. Есептіңблок-сұлбасынқұрыңыз.

3. MatLab ортасында есептің шешімі болатындай бағдарлама жазыңыз.

1.5- кесте

Нұсқа	Х10	Нұсқа	Х8	Нұсқа	Х16
1	45	4	32	7	17
2	13	5	25	8	34
3	58	6	52	9	22

Бақылау сұрақтары:

1. Санау жүйесі дегеніміз не?

2. Қандай санау жүйесін білесіздер?

3. Санау жүйесін түрлендіру заңдылықтарын атаңыз.

4. Жүйенің алгоритмін тусіндірініз.

№2 Зертханалық жұмыс

Логикалық элементтер көмегімен логикалық

функцияларды оқу

Жұмыстың мақсаты: Әртүрлі логикалық функциялардың жұмысын іске асыратын, логикалық элеменптер негізінде жасалған электронды сұлбаларды құрады және модельдеуді үйрену.

Қысқаша теориялық кіріспе

Логикалық элементтер - логика ашгебрасы ережелеріне сәйкес, кіріс сигналдары мен карапайым логикалық операцияларды (функцияларды) жүзеге асыратын электрондық кұрылғылар. Логикалық операцияның операндасы екілік санау жүйесінде беріледі, сондықтан логикалық элементтердің кірісі жоғарғы немесе төменгі деңгейлі сигналдарды қабылдайды. Сәйкесінше, кернеудің ЖОғарғы деңгейі (логикалық кернеу 1) операнданың ақикат мәнін көрсетеді, ал төменгі деңгей (логикалық кернеу 0) жалған мәнін көрсетеді. Кернеудің жоғарғы және тәменгі денгей мәндері логикалық элементтер сұлбасының электрлік параметрлерімен аныкталынады. Көп жағлайларда логикалык элементтер жеке интегралды микросұлба ретінде жиналады. Логикалық элементтер орындайтын логикалық операцияларға келесілер жатады: конъюнкция (логикалық көбейту, және), дизіюнкция (логикалық қосу. НЕМЕСЕ), терістеу (ЕМЕС). 2 модулі бойынша қосу (НЕМЕСЕ шектеу).

---

Логикалық элементтердің негізгі түрлері:

Логикалық ЖӘНЕ элементі. Логикалық ЖӘНЕ элементі кіріс мандеріне сәйкес логикалык көбейту (конъюнкция) операциясын орындайды және оның 2-ден 8-ге дейін кіріні, сондай-ақ бір шығысы болады. 2.1 -суретте екі кірісі бар ЖӘНЕ логикалық элементінің шартты графикалық белгіленуі (ШГБ) көрсетілген.ЖӘНЕ элементі NЖӘНЕ ретінде белгіленеді, мұндағы N - логикалық элементтерлің кірістерінін саны (мысалы, 2 ЖӘНЕ, және, және және т.б.).



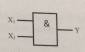
2.1- сурет. Екі кірісі бар ЖӘНЕ логикалық элементінің шартты

графикалык белгіленуі

2.1- кесте

2 ЖӘНЕ элементінің ақиқат кестесі

Х1	Х2	Y
0	0	0
1	0	0
0	1	0
1	1	1

Логикалық НЕМЕСЕ элементі. НEMECE логикалық элементі өзінің кіріс мәндеріне логикалық қосу (дизъюнкция) операциясын орындайды, логикалық элементі секілді бірнеше кірісі болуы мүмкін. 2.2-суретте екі кірісі бар НЕМЕСЕ логикалық элементтің ШГБ көрсетілген.



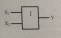
2.2-сурет. Екі кірісі бар HEMECE логикалық элементінің шартты

графикалық белгіленуі

2.2- кесте

2HEMECE логикалық элементінін ақиқат кестесі

Х1	Х2	Y
0	0	0
1	0	1
0	1	1
1	1	1

Логикалық ЕМЕС элементі (инвертор). Логикалык EMEC элементі өзінің кіріс мәндеріне терістеу операциясын орындайды және оның бір кірісі, сондай-ақ бір шығысы болады.Кейде оны инвертор деп атайды

---

Смотрите также файлы

• Сйлеуді дамыту теориясы мен дістемесі.docx

• Воп для вступительных экзаменов в интернатуру 5 курс.docx

• Ear diseases хвороби вух structure of the Ear.docx

• А.нанбаев. алы елім, азаым, айран жртым леі.docx

• Инструкция по конфиденциальному делопроизводству в организации включает те же разделы, что и инструкция по общему делопроизводству, но в ней необходимо отразить особенности работы с конфиденциальными документами.docx