Файл: MatLab ортасында сандарды онды жне екілік санау жйесіне айналдыру алгоритмін жзеге асыру Жмысты масаты.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 255
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, себебі ол кіріс сигналды инверттейді. 2.3-суретте EMEC элементінің ШГБ көрсетліген.

2.3-сурет. Логикалық ЕМЕС элементтерінің шартты траф, халық белгіленуі
2.3-кесте
EMEC элементінің ақиқат кестесі
Сонымен қатар екі немесе бірнеше логикалық элементтерден құрастырылған логикалық элементтер болады, оларды комбинациялық логикалық элементтер деп атайды. Кейбір комбинатциялык элементтерді қарастырайық.
ЖӘНЕ-ЕМЕС логикалық элементі өзінің кіріс мәндеріне логикалық көбейту операциясын орындайды, содан кейін алынған нәтижені терістейді және шығысына береді. Осылай,ЖӘНЕ- ЕМЕС логикалық элементін шығысында инверторы бар ЖӘНЕ элементі деп те атауға болалы. 2ЖӘНЕ-ЕМЕС элементтің ШГБ 2.4-суретте көрсетілген.
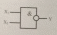
2.4-сурет. Екі кірісті және-ЕМЕС логикалық элементінің ШГБ
2.4-кесте
2ЖӘНЕ-ЕМЕС элементінің ақиқат кестесі
НЕМЕСЕ-ЕМЕС элементі. НЕМЕСЕ-ЕМЕС логикалық элементі, өзінің кіріс мәндеріне қосу амалдарын орындайды,содан кейін нәтижесін инверттейді және шығысына жібереді.Осылай, НЕМЕСЕ-ЕМЕС логикалық элементін шығысында инверторы бар НЕМЕСЕ логикалық элементі деп атауға болады.2.5-суретте НЕМЕСЕ-ЕМЕС элементтің ШГБ көрсетілген.
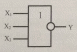
2.5-сурет. Үш кірісті НЕМЕСЕ-ЕМЕС логикалық элементінің ШГБ
2.5-кесте
3HEMECE-EMEC элементінің ақиқат кестесі
HEMECE шектеу элементі. НЕМЕСЕ шектеу логикалык элементі практика жүзінде көп қолданылмайды. НЕМЕСЕ шектеу немесе 2 модулі бойынша қосу функциясын былай түсіндірілсе немесе барлық кірістеріне нөл берген кезде, онда шығысында "1" шығады. Егер кірісіне екі "1" деген сигнал берілсе немесе барлық кірістеріне нөл берген кезде, онда шығысында нөл шығады. НЕМЕСЕ шектеу элементіндегі "=1" жазу, тек бір кірісіне ғана «1» мәнін беру керек екендігін білдіреді.
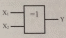
2.6-сурет. НЕМЕСЕ шектеу логикалық элементінің ШГБ
2.6-кесте
НЕМЕСЕ шектеу элементінің ақиқат кестесі
НЕМЕСЕ-ЕМЕС шектеу элементі. НЕМЕСЕ-ЕМЕС шектеу логикалық элементі кірісіне бірдей мәндер берген жағдайда ғана шығысында 1 шығады.
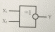
2.7-сурет. НЕМЕСЕ-ЕМЕС шектеу логикалық элементінің ШГБ
2.7-кесте
НЕМЕСЕ-ЕМЕС шектсу элементінің ақиқат кестесі
Kipiс мәндеріне логикалық операцияларды орындайтын күрделі логикалык элементтер де болады. Мысалы, 2ЖӘНЕ-HEMECE, оның ШГБ 2.8- суретте көрсетілген, алдымен, X1, Х2 және Х3, Х4 операндаларға логикалык көбейту операциясын орындайды, содан кейін алынған нәтижелерге логикалық қосу операциясы орындалады, яғни оның логикалық функциясы келесі түрде болады: y = x1x2 + x3x4.
Бұдан да қиын комбинациялық логикалық элементтерді кұрастыруға болады, мысалы, 3-2 ЖӘНЕ-НЕМЕСЕ-ЕМЕС (2.9-сурет).

2.8-сурет. 2ЖӘНЕ-НЕМЕСЕ логикалық элементінің сұлбасы (а) жане ШГБ (э).
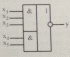
2.9-сурет. 3-2 ЖӘНЕ-НЕМЕСЕ-ЕМЕС логикалық элементінің ШГБ
Зертханалық жұмыстың орындалу реті:
1. 2.8 кесте берілген нұсқа бойынша логикалық функцияның ақиқат кестесін толтырыңыз (2.9-кестедегі “Хе “ бағаны).
2. Логикалық элементтерді қолдана отырып, Multisim ортасында функцияның сұлбасын жинаңыз және 2.9-кестедегі "Хm"бағанын толтырыңыз.
3. 2.9-кестедегі "Xe" бағаны мен "Xm" бағанының сәйкес келетініне көз жеткізіңіз.
2.8-кесте


2.9-кесте
Функцияның ақиқат кестесі
Аңгартпа: Ақиқат кестесін толтыруға нұсқау.a,b, cбағандарына сәйкесінше логикалық айнымалылардың мәндері жазылады.Ал хе бағанында аналитикалық жолмен есептелген логикалық функция мәндерін жазу қажет.Соңғы бағанда хмMultiSimортасында жиналған сұлбада жүргізілген тәжірибе жолымен алынған мәндер жазылады.
Бақылау сұрақтары:
2. Логикалық элементтердің ақиқат кестесі.
3. Комбинацилық элементтерге мысал келтіріңіз.
№3 зертханалық жұмыс
Логикалық өрнектер мен функцияларды
Бұл алгебрасының сәйкестік зандылықтары
көмегімен ықшамдау
Жұмыстың мақсаты: логикалық өрнектерді ықшамдаудың әдіс -
тәсілдерін менгеру,канал кестесін қолдана отырып, логикалық функциялардың сәйкестігін көрсету. Сонымен катар ықшамдалған логикалық өрнектерді электрондық сұлбаларын компьютерлік модельдеу тәсілдерімен танысу.
Қысқаша теориялық кіріспе
Сандық электроникада логикалық айнымалыларға қатысты коньюнкция (логикалық кебейту), лизьюнкция (логикалық косу) және инверсия (логикалық терістеу) деп аталатын бірнеше негізгі операциялар орындалады. Логикалык өрнектермен жұмыс істеген кезде күрделі аналитикалық теңдеулер кездеседі, олардың; сұлбасын кұрастыру және ақиқат кестесін толтыру қиындатылада, сондықтан күрделі аналитикалық теңдеулерді, ең алдымен, карапайым түрге келтіріп алған дұрыс. Ол үшін Бул алгебрасының сәйкестік заңдылықтары қолданылады. Төменде логикалық алгебраның негізгі заңдылыктары келтірілген.
Логика алгебрасының сәйкестік заңдылықтары:
1. Ауыстырылымдылық заңы.
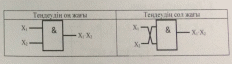
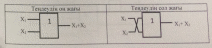
2.1. Конъюнкция үшін :
Y = (X1 * X2) * X3 =( X2 * X3) * X2 =X1 * X2 * X3.
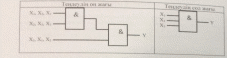

2.3-сурет. Логикалық ЕМЕС элементтерінің шартты траф, халық белгіленуі
2.3-кесте
EMEC элементінің ақиқат кестесі
| Х | Y |
| 0 | 1 |
| 1 | 0 |
Сонымен қатар екі немесе бірнеше логикалық элементтерден құрастырылған логикалық элементтер болады, оларды комбинациялық логикалық элементтер деп атайды. Кейбір комбинатциялык элементтерді қарастырайық.
ЖӘНЕ-ЕМЕС логикалық элементі өзінің кіріс мәндеріне логикалық көбейту операциясын орындайды, содан кейін алынған нәтижені терістейді және шығысына береді. Осылай,ЖӘНЕ- ЕМЕС логикалық элементін шығысында инверторы бар ЖӘНЕ элементі деп те атауға болалы. 2ЖӘНЕ-ЕМЕС элементтің ШГБ 2.4-суретте көрсетілген.

2.4-сурет. Екі кірісті және-ЕМЕС логикалық элементінің ШГБ
2.4-кесте
2ЖӘНЕ-ЕМЕС элементінің ақиқат кестесі
| Х1 | Х2 | Y |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
НЕМЕСЕ-ЕМЕС элементі. НЕМЕСЕ-ЕМЕС логикалық элементі, өзінің кіріс мәндеріне қосу амалдарын орындайды,содан кейін нәтижесін инверттейді және шығысына жібереді.Осылай, НЕМЕСЕ-ЕМЕС логикалық элементін шығысында инверторы бар НЕМЕСЕ логикалық элементі деп атауға болады.2.5-суретте НЕМЕСЕ-ЕМЕС элементтің ШГБ көрсетілген.

2.5-сурет. Үш кірісті НЕМЕСЕ-ЕМЕС логикалық элементінің ШГБ
2.5-кесте
3HEMECE-EMEC элементінің ақиқат кестесі
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
HEMECE шектеу элементі. НЕМЕСЕ шектеу логикалык элементі практика жүзінде көп қолданылмайды. НЕМЕСЕ шектеу немесе 2 модулі бойынша қосу функциясын былай түсіндірілсе немесе барлық кірістеріне нөл берген кезде, онда шығысында "1" шығады. Егер кірісіне екі "1" деген сигнал берілсе немесе барлық кірістеріне нөл берген кезде, онда шығысында нөл шығады. НЕМЕСЕ шектеу элементіндегі "=1" жазу, тек бір кірісіне ғана «1» мәнін беру керек екендігін білдіреді.

2.6-сурет. НЕМЕСЕ шектеу логикалық элементінің ШГБ
2.6-кесте
НЕМЕСЕ шектеу элементінің ақиқат кестесі
| Х1 | Х2 | Y |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
НЕМЕСЕ-ЕМЕС шектеу элементі. НЕМЕСЕ-ЕМЕС шектеу логикалық элементі кірісіне бірдей мәндер берген жағдайда ғана шығысында 1 шығады.

2.7-сурет. НЕМЕСЕ-ЕМЕС шектеу логикалық элементінің ШГБ
2.7-кесте
НЕМЕСЕ-ЕМЕС шектсу элементінің ақиқат кестесі
| Х1 | Х2 | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Kipiс мәндеріне логикалық операцияларды орындайтын күрделі логикалык элементтер де болады. Мысалы, 2ЖӘНЕ-HEMECE, оның ШГБ 2.8- суретте көрсетілген, алдымен, X1, Х2 және Х3, Х4 операндаларға логикалык көбейту операциясын орындайды, содан кейін алынған нәтижелерге логикалық қосу операциясы орындалады, яғни оның логикалық функциясы келесі түрде болады: y = x1x2 + x3x4.
Бұдан да қиын комбинациялық логикалық элементтерді кұрастыруға болады, мысалы, 3-2 ЖӘНЕ-НЕМЕСЕ-ЕМЕС (2.9-сурет).

2.8-сурет. 2ЖӘНЕ-НЕМЕСЕ логикалық элементінің сұлбасы (а) жане ШГБ (э).

2.9-сурет. 3-2 ЖӘНЕ-НЕМЕСЕ-ЕМЕС логикалық элементінің ШГБ
Зертханалық жұмыстың орындалу реті:
1. 2.8 кесте берілген нұсқа бойынша логикалық функцияның ақиқат кестесін толтырыңыз (2.9-кестедегі “Хе “ бағаны).
2. Логикалық элементтерді қолдана отырып, Multisim ортасында функцияның сұлбасын жинаңыз және 2.9-кестедегі "Хm"бағанын толтырыңыз.
3. 2.9-кестедегі "Xe" бағаны мен "Xm" бағанының сәйкес келетініне көз жеткізіңіз.
2.8-кесте


2.9-кесте
Функцияның ақиқат кестесі
| a | b | c | xe | xm |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
Аңгартпа: Ақиқат кестесін толтыруға нұсқау.a,b, cбағандарына сәйкесінше логикалық айнымалылардың мәндері жазылады.Ал хе бағанында аналитикалық жолмен есептелген логикалық функция мәндерін жазу қажет.Соңғы бағанда хмMultiSimортасында жиналған сұлбада жүргізілген тәжірибе жолымен алынған мәндер жазылады.
Бақылау сұрақтары:
-
Логикалық элементтер дегеніміз не?
2. Логикалық элементтердің ақиқат кестесі.
3. Комбинацилық элементтерге мысал келтіріңіз.
№3 зертханалық жұмыс
Логикалық өрнектер мен функцияларды
Бұл алгебрасының сәйкестік зандылықтары
көмегімен ықшамдау
Жұмыстың мақсаты: логикалық өрнектерді ықшамдаудың әдіс -
тәсілдерін менгеру,канал кестесін қолдана отырып, логикалық функциялардың сәйкестігін көрсету. Сонымен катар ықшамдалған логикалық өрнектерді электрондық сұлбаларын компьютерлік модельдеу тәсілдерімен танысу.
Қысқаша теориялық кіріспе
Сандық электроникада логикалық айнымалыларға қатысты коньюнкция (логикалық кебейту), лизьюнкция (логикалық косу) және инверсия (логикалық терістеу) деп аталатын бірнеше негізгі операциялар орындалады. Логикалык өрнектермен жұмыс істеген кезде күрделі аналитикалық теңдеулер кездеседі, олардың; сұлбасын кұрастыру және ақиқат кестесін толтыру қиындатылада, сондықтан күрделі аналитикалық теңдеулерді, ең алдымен, карапайым түрге келтіріп алған дұрыс. Ол үшін Бул алгебрасының сәйкестік заңдылықтары қолданылады. Төменде логикалық алгебраның негізгі заңдылыктары келтірілген.
Логика алгебрасының сәйкестік заңдылықтары:
1. Ауыстырылымдылық заңы.
-
1. Конъюнкция үшін: X1 * X2 = X2 * X1 .

-
Дизъюнкция үшін : X1 + X2 = X2 + X1.

-
Келісімділік заңы.
2.1. Конъюнкция үшін :
Y = (X1 * X2) * X3 =( X2 * X3) * X2 =X1 * X2 * X3.
