2.2. Дизъюнкция үшін: 

Y = ( X₁ + X₂) + X₃ = (X₂ + X₃) + X₁ = (X_{1 +} X₃) + X₂ = X₁ + X₂ + X_3. 

3. 
    Таралымдылық заңы. 
   

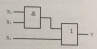
3.1. Конъюнкция үшін : 

Y = X₁ * (X₂ + X₃) = X_{1 *} X₂ + X₁ * X_3. 

Теңдеудің оң жағы

 

                                                                                 Теңдеудің сол жағы 



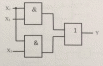
3.2. Дизъюнкция үшін : 

Y = X₁ + (X₂ * X₃) = (X₁ + X₂) * ( X₁ + X₃).
Теңдеудің оң жағы 



                                                                                 Теңдеудің сол жағы 

3. 
   Инверсия заңы (де Морган заңы).
   

4.1. Конъюнкция үшін :Y = X₁ * X₂ = X̄₁ + X̄_2.

Теңдеудің оң жағы 



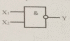
                                                                                 Теңдеудің сол жағы 


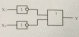
4.2. Дизъюнкция үшін : Y = X₁ + X₂ = X̄₁ * X̄_2.

Теңдеудің оң жағы 



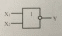
                                                                                 Теңдеудің сол жағы 

3. 
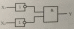
   Қайталану заңы.
   

5.1. Конъюнкция үшін : X = X * X *X*…*X.

Теңдеудің сұлбасы



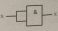
5.2. Дизъюнкция үшін : X = X + X +X + …+X

Теңдеудің сұлбасы

3. 
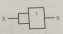
   Қос терістеу заңы : Х = Х̿
   

Теңдеудің сұлбасы



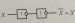
7. Қабысу заңы.

7.1. Конъюнкция үшін : (X₁ + X₂) * (X₁ + X̄₂) = X_1.

Теңдеудің сұлбасы



7.2. Дизъюнкция үшін : (X₁ * X₂) + (X₁ * X̄₂) = X_1.

Теңдеудің сұлбасы

8. 
   Жұтылу заңы.
   
   1. 
      Х₁ * (X₁ + X₂) = X₁.
      

Теңдеудің сұлбасы

---

2. 
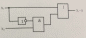
   Х₁* (х̄₁ + Х₂) = Х₁ * Х₂.
   

Теңдеудің оң жағы 



                                        Теңдеудің сол жағы

3. 
   Х₁+ Х₁ *Х₂ = Х₁
   

Теңдеудің сұлбасы

4. 
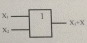
   Х₁ + х̄₁ * Х₂= Х₁ + Х₂.
   

Теңдеудің оң жағы



                                                           Теңдеудің сол жағы 

8. 
   0 және 1 қатынастар заңы.
   
   1. 
      Конъюнкция үшін:
      

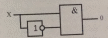
X * 0 = 0 X * 1 =1


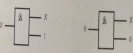
Теңдеудің сұлбалары


Х * Х̅ = 0

Теңдеудің сұлбасы

2. 
   Дизъюнкция үшін:
   

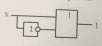
X + 0 = X X + 1 = 1

Теңдеудің сұлбалары



Х + Х̅ = 1

Теңдеудің сұлбасы


10.НЕМЕСЕ- ШЕКТЕУ логикалық элементіне төмендегідей заңдар қолданылады:

1. Қайталану заңы: x 0 = x

2. Терістеу заңы׃ х 1 = х̅

3. Ауыстырылымдылық:x 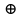x₀ = x₀ 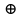x

4. Келісімділік : (x 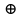x₀ ) 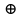x₁ = x (x₀ x₁)

5. Модуль бойынша салыстыру заңы : x x₀ = x x̅₀ = (x = x₀) ;

6. x x = 0

7. (x x₀)

---

x₀ = x.

Зертханалық жұмыстың орындалу реті:

1. 
   3.2-кестеде көрсетілген нұсқа бойынша логикалык функцияның мәндерін есептей отырып, акиқат кестесін толтырыңыз(3.1-кесте). MultiSim ортасында логикалык элементтерді қолдана отырып, берілген логикалық функцияның электрондық сұлбасын жинаңыз. Электрондық сұлба бойынша тәжірибелік өлшеулер өткізіп, соған сәйкес ақиикат кестесін толтырыңыз. Есептелген және тәжірибеден алынған акиқат кесіелерін өзара салыстырыңыз және олардың сәйкестігіне көз жеткізіңіз.
   

3.1-кесте

Логикалық функцияның ақиқат кестесі

а	В	…n	Аналитикалық жолмен есептеу	Схемотехникалық жолмен алынған нәтиже
. . .

2. Логика алгебрасының заңдарын қолдана отырып, беріліген логикалық функцияны ықшамдаңыз. MultiSim ортасында ықшамдалған Функцияға сәйкес электрондық сұлбасын жинаңыз. Осы сұлба бойынша тәжірибелік өлшеулер жүргізе отырып, ықшамдалған функцияның ақиқат кестесін толтырыңыз.

3. 1 және 2-пункте алынган акиқат кестелерінін сәйкестігіне көз жеткізіңіз.

3.2- кесте



Бақылау сұрақтары:

1. 
   Логика алгебра заңдарын қолдану не себепті тиімді болып табылады?
   
2. 
   Бул алгебрасының негізгі заңдарын атаңыз.
   
3. 
   Ықшамдалған функция мен ықшамдалмаған функцияның ақиқат кестесі сәйкес болуы шарт па?
   
4. 
   Ықшамдаудың негізгі артықшылықтарын атаңыз.
   

№4 зертханалық жұмыс

ЖДНФ және ЖКНФ көмегімен айнымалы фунцияның логикалық теңдеуін құру

---

Жұмыстың мақсаты: жеткілікті диъюнктивті нормал формасы және жеткілікті конъюнктивті нормал формасы мен танысу

Қысқаша теориялық кіріспе

Коньюнкцияның, дизъюнкцияның және терістеудің касиеттері:

1. n айнымалыларының конъюнкциясы: кіріс айнымалы мәндерінің барлығы 1-ге тең болған жағдайда, шығыс функцияның мәні тек 1-ге тең болады, яғни осы айнамалылардың біреуі 0-ге тең болса, онда функцияның шығысы 0 болады.

2. n айнымалыларының дизьюнкциясы: егер барлық айнымалылар 0 деңгейде болса, онда функция 0-ге тең болады, ал айнымалылардың біреуі жоғарғы деңгейді қабылдаса, онда функция 1 –ге тең болады.

Екі функция айнымалылардың ретіне байланыссыз орындала береді.

Қарапайым конъюнкция деп бір немесе бірнеше айнымалылардың олардың көбейтіндісін айтамыз, сонымен қатар әрбір айнымалы тек бір рет қана (айнымалының өзі немесе оның терісі) кездеседі. Мысалы, х * y * z̅ функциясы қарапайым конъюнкция болып табылады.

Дизьюнкцияның нормал формасы (ДНФ) дегеніміз - қарапайым конъюнкцияның қосындысы. Мысалы, x * y + y̅ * z – бұл ДНФ.

Жеткілікті дизьюнкцияның нормал формасы деп әрбір конъюнкцияға барлық айнымалылар (айнымалылардың өздері немесе олардың теріс мәндері) кіретін дизьюнктивті нормал формасын айтады.

Мысалы, х + у̅ * z ДНФ болып табылады, бірақ ол ЖДНФ емес. Ал егер функцияны x * y * z + x * y̅ *z̅ + x̅ * y *z түрде болса, онда ол ЖДНФ болады.

№5 Зертханалық жұмыс

Жартылай және толық сумматорлар

Жұмыстың мақсаты: Жартылай және толық сумматор жұмысын зерттеу. Көп разрядты толық сумматорды бір разрядтық толық сумматорлар көмегімен кұрастыруды үйрену.

Қысқаша теориялық кіріспе

Екілік сандарды қосу кәдімгі ондық сандарды қосқан сияқты жүргізіледі. Екілік сандарды қосу үшін оның әрбір разряды үшін мынадай ереже қолданылады:

0 + 0 = 0

0+1 = 1

1 + 0 = 1

1+1 = 0+ (1 - ойда)

Осы айтылған ереженің НЕМЕСЕ ШЕКТЕУ (XOR) функциясының логикасына сай келетіндігі анық байқалады. Сонымен қатар сандарды қосу кезінде «ойға тастау» амалын бір мезгілде орындап отыру қажет. Мысал ретінде ондық жүйедегі 3 және 5 сандарының екілік жүйедегі қосындысын есептеу жолын көрсетейік:

1 1 1Ойға тастау

0 1 0 1 Қосылғыш( 5)

0 0 1 1 Қосылғыш ( 3)

1 0 0 0 Қосынды ( 8)

Осы мысалдан «ойға тастау» амалына сай келетін логиканың ақиқат кестесі төменде көрсетілген.

5.1-кесте

Қосылғыш 1	Қосылғыш 2	Ойға тастау
0	0	0
0	1	0
1	0	0
1	1	1

---

5.1-кестедегі ақиқат кестесіндегі ойға тастау бағаны ЖӘНЕлогикалық функциясына сай келеді.

Сонымен, сандарды қосу амалы екі кезеңнен тұрады:

1. Қосылғыштардың разрядын өзара қосу.

2. Бірінші кезеңде алынған нәтижеге ой да жиналған санды сәйкес разрядтар бойынша қосу.

Әрбір кезеңді жеке орындайтын логикалық құрылғы жартылай сумматор деп аталады. Жартылай сумматор шығысындаекі түрлі мәнге ие болады, ал оның логикасының ақиқат кестесі 5.2-кестеде келтірілген.

5.2-кесте

Жартылай сумматордың ақиқат кестесі

Кіріс			Шығыс
А		В	С		S
0		0	0		0
0		1	0		1
1		0	0		1
1	1		1	0

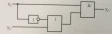
Мұндағы А және В - қосылғыштар, С - ойға тастау, ал S - жартылай сумматордың жұмыс нәтижесі.

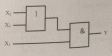
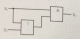
Төменде жартылай сумматордың логикасын сипаттайтын сұлба келтірілген.



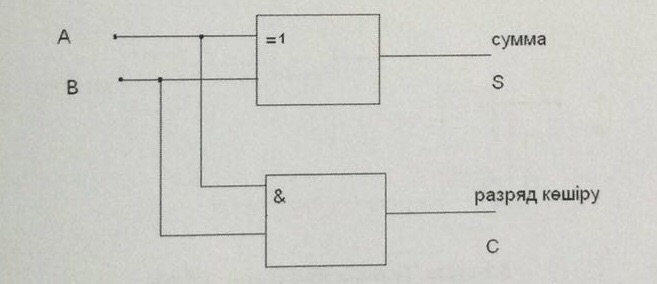
5.1-сурет. Жартылай сумматордың құрылымдық сұлбасы

Жартылай сумматордың жұмыс логикасын мынадай аналитикалық өрнектермен сипаттауға болады:

S = A + B;

C = A*B.

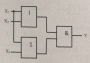
Жартылай сумматор қосынды нәтижесін толықтай бермейді, сол себепті сандарды қосу үшін қажетті құрал екі жартылай сумматордан тұруы қажет. Екі жартылай сумматордан құралғансұлба - толық сумматор деп аталады.

Толық сумматордың ақиқат кестесі 5.3-кестеде және оның логикасын сипаттайтын сұлбасы 5.2-суретте көрсетілген.

5. 3-кесте

---

Смотрите также файлы

• Сйлеуді дамыту теориясы мен дістемесі.docx

• Воп для вступительных экзаменов в интернатуру 5 курс.docx

• Ear diseases хвороби вух structure of the Ear.docx

• А.нанбаев. алы елім, азаым, айран жртым леі.docx

• Инструкция по конфиденциальному делопроизводству в организации включает те же разделы, что и инструкция по общему делопроизводству, но в ней необходимо отразить особенности работы с конфиденциальными документами.docx