4. 
   Для того, чтобы разрушить мост, нужно по­падание не менее двух бомб. Независимо сбросили три бом­бы с вероятностями попадания 0.1, 0.3 и 0.4. Какова вероятность, что мост разрушен?
   

5. 
   Число грузовых машин, проезжающих мимо колонки, относится к числу легковых машин как 3:2. Вероят­ность того, что грузовая машина будет заправляться равна 0.1, а того, что будет заправляться легковая - 0.2. У бензо­колонки заправляется машина. Найти вероятность того, что это грузовая машина.
   

6. 
   В помещении четыре лампы. Вероятность ра­боты в течение года для каждой лампы 0.8. Найти вероят­ность того, что к концу года горят три лампы. Чему равно наивероятнейшее число ламп, которые будут работать в те­чение года?
   

7. 
   Годовое потребление угля некоторым предприятием является нормальной случайной величиной с математическим ожиданием 1327 т. и с.к.о. 28 т. Сколько угля надо запасти, чтобы с вероятностью 0,95 его хватило бы на год? Если запасено 1360 т, то с какой вероятностью этого хватит?
   

Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.107

1. 
   Случайная точка равномерно распределена внутри квадрата со стороной, равной а . Найти вероятность того, что расстояние от центра квадрата до точки меньше а/2.
   

2. 
   При наборе телефонного номера абонент за­был две последние цифры и набрал их наудачу, помня толь­ко, что эти цифры нечетные и разные. Найти вероятность того, что номер набран правильно.
   

3. 
   Для того, чтобы сбить самолет достаточно одного попадания. Было сделано три выстрела с вероятно­стями попаданий 0.1, 0.2 и 0.4 соответственно. Какова веро­ятность того, что самолет сбит?
   

4. 
   Какова вероятность выпадения хотя бы двух шестерок при трех бросаниях игральной кости?
   

5. 
   Имеются две урны: в первой а белых шаров и bчерных; во второй с белых и dчерных. Из первой урны во вторую перекладывают не глядя один шар. После этого из второй урны берут один шар. Найти вероятность того, что этот шар будет белым. Известно, что вышел белый. Какова вероятность того, что был переложен черный?
   

---

6. 
   Изделие идет первым сортом, если отклонение размера от номинала не превосходят по модулю 3.5 мм. Отклонения нормальны с с.к.о., равным 3 мм. Систематические отклонения отсутствуют. Найти математическое ожидание числа изделий первого сорта, если сделано было 4 изделия.
   

7. 
   Есть правильный кубик, у которого на про­тивоположных гранях написаны цифры 1,2 и 3 соответствен­но. Пусть X- число единиц, выпавших при трех бросаниях кубика. Найти закон распределения, вычислить математи­ческое ожидание и дисперсию Х.
   

Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.108

1. 
   Студент ездит в университет двумя автобусами. Время ожидания первого равномерно распределено в интервале ( 0 – 4 мин), а второго – (0 – 9мин). Какова вероятность того, что время ожидания первого превысит время ожидания второго автобуса?
   

2. 
   В ящике 10 красных и 6 белых шаров. Вы­нимаются наудачу два шара. Какова вероятность того, что шары будут одноцветными?
   

3. 
   Какова вероятность того, что при многократ­ном бросании правильной монеты герб впервые выпадет на четном броске?
   

4. 
   Два баскетболиста делают по три броска в корзину. Вероятность попадания мяча при каждом броске равна соответственно 0.6 и 0.7. Найти Вероятность того, что у обоих будет равное количество попаданий.
   

5. 
   Приборы одного наименования изготовляются двумя заводами; первый завод поставляет 2/3 всех изделий, поступающих на производство; второй 1/3. Надежность (Вероятность безотказной работы) прибора, изготовленного первым заводом, равна р₁ ; второго р₂. Определить полную (среднюю) надежность р прибора, поступившего на производство.
   

6. 
   Один игрок бросает три монеты, а другой две. Найти закон распределения случайной величины – общее число выпавших гербов.
   

7. 
   Плотность с.в.Х такова
   

Н
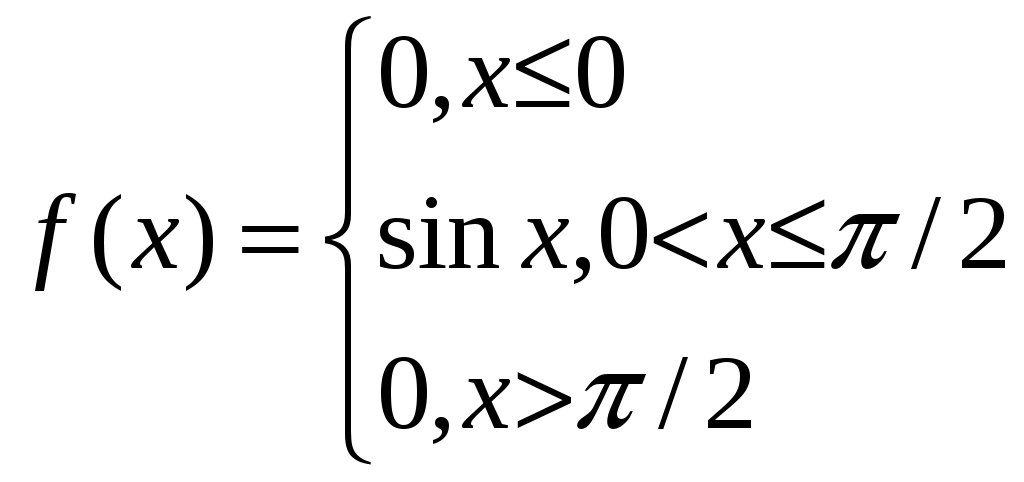
айти функцию распределения, числовые характеристики и вероятность того, что с.в.Х хотя бы два раза попадет в интервал (0, π/6) в четырех испытаниях.

---

Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.109

1. 
   Найти вероятность того, что наудачу взятое двузначное число окажется кратным 2, либо 5, либо тому и другому одновременно.
   

2. 
   Какова Вероятность того, что при многократ­ном бросании игральной кости шестерка впервые выпадет на четвертом броске?
   

3. 
   Партия изделий содержит 1 % брака. Каков должен быть объем контрольной выборки, чтобы вероятность обнаружить в ней хотя бы одно бракованное изделие была не меньше 0.95.
   

4. 
   Имеется две партии однородных изделий; первая партия со­стоит из N изделий, среди которых п дефектных; вторая партия — из М изделий, среди которых т дефектных. Из первой партии берется слу­чайным образом К. изделий, а из второй Lизделий (К. <. N; L< М); эти К + Lизделий смешиваются и образуется новая партия. Из новой смешанной партии берутся наугад два изделия. Найти вероятность того, что оба будут дефектным.
   

5. 
   В семье 5 детей. Найти вероятность того, что среди детей два мальчика; не более двух мальчиков; более двух мальчиков; не менее двух и не более трех мальчиков. Вероятность рождения мальчика принять равной 0,51.
   

6. 
   Дана функция распределения случайной величины Х
   

Найти плотность распределения, числовые характеристики. Найти вероятность того, что в четырех независимых испытаниях с.в.Х два раза попадет в интервал (0,2;0,6).

7. 
   Диаметр втулки должен быть равен 7,5 мм. Ошибки изготовления нормальны с m=0 и =0,05 мм. Если ошибка не превышает по модулю 1%, то втулка идет первым сортом. Какова вероятность того, что втулка будет первого сорта?
   

8. 
   Два баскетболиста поочередно бросают мяч в корзину до первого попадания. Вероятность попадания первого – 0,6, а второго – 0,3. Найти закон распределения числа бросков до первого попадания.
   

---

Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.110

1. 
   В круг радиуса R вписан правильный треугольник. Затем внутрь круга наугад брошены 4 точки. Найти вероятности следующих событий: а) все 4 точки попали в треугольник, б) одна в треугольнике и три в каком-то малом сегменте.
   

2. 
   Бросаются 4 игральные кости. Найти вероятность того, что на них выпадет по одинаковому числу очков.
   

3. 
   Завод изготовляет изделия, каждое из которых с вероятностью r (независимо от других) оказывается дефектным. При осмотре дефект, если он имеется, обнаруживается с вероятностью р. Для конт­роля из продукции завода выбирается n изделий. Найти вероятности следующих событий:
   

A = {ни в одном из изделий не обнаружено дефекта}; B = {среди п изделий ровно в двух обнаружен дефект}; С = {среди п изделий не менее чем в двух обнаружен дефект}.

4. 
   Имеется два ящика, в которых находятся однотипные изделия; некоторые из них исправны, другие — дефектны. В первом ящике а исправных изделий и bдефектных, во втором — с исправных и dдефектных. Из первого ящика во второй перекладывают наугад одно изделие, его смешивают с другими, после чего из второго ящика в пер вый перекладывают обратно одно наугад выбранное изделие. После всего этого из первого ящика берут наугад одно изделие. Найти вероятность того, что оно будет исправным.
   

5. 
   Один игрок бросает три монеты, а другой две. Найти закон распределения случайной величины – общее число выпавших гербов.
   

6. 
   Семь шаров пронумерованы числами 0, 1, 1, 2, 2, 2 и 10 и помещены в урну. Произвольным образом выбирается один шар, и если он имеет номер п, то игрок получает п долларов. Каково математическое ожидание выигрыша?
   

7. 
   Годовое потребление угля некоторым предприятием является нормальной случайной величиной с математическим ожиданием 327 тонн и с.к.о. 28 тонн. Сколько угля надо запасти, чтобы с вероятностью 0,95 его хватило бы на год? Если запасено 395 тонн, то с какой вероятностью этого хватит?
   

---

Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.111

1. 
   На девяти карточках написаны цифры: 0, 1,2, 3, 4, 5, 6, 7, 8. Две из них вынимаются наугад и укладываются на стол в порядке появления, затем читается полученное число, например 07 (семь), 14 (четырнадцать) и т. п. Найти вероятность того, что число будет четным.
   

2. 
   Имеются два ящика, содержащих типовые элементы замены (ТЭЗ). В первом ящике а исправных ТЭЗ и bнеисправных; во втором — с исправных и dнеисправных. Из каждого ящика наугад вынимается по одному ТЭЗ. Найти Вероятность того, что оба ТЭЗ будут исправны­ми. Найти вероятность того, что оба вынутых ТЭЗ будут неисправны.
   

3. 
   При въезде в новую квартиру в осветительную сеть было включено 2kновых электролампочек. Каждая лампочка в течение года перегорает с вероятностью p. Найти вероятность события А = {в течение года не менее половины первоначально включенных лампочек придется заменить новыми}.
   

4. 
   Цех производит изделия; любое из них с вероятностью р имеет дефект. Каждое изделие осматривается браковщиком, который обнаруживает дефект, если он имеется, с Вероятностью р₁и не обнаруживает — с вероятностью 1 — р₁ . Кроме того, иногда браковщик допускает ошибку, бракуя доброкачествен­ное изделие; это происходит с вероятностью р₂. За смену браковщик осматривает N изделий. Найти вероятность Rтого, что хотя бы одно из них будет квалифицировано им неправильно: то есть, будучи дефект­ным, отнесено к доброкачественным, или же наоборот (считается, что результаты осмотра отдельных изделий независимы).
   

5. 
   Случайная величина Х имеет распределение
   

xi	-3	-2	0	1	3
pi	0,2	0,3	0,2	0,2	0,1

---

Смотрите также файлы

• Существенным фактором для любой хорошо функционирующей социальной системы являются социальная защита, социальная и экономическая поддержка населения.docx

• 1 Теоретические и методические аспекты анализы прибыли и ее налогообложения.docx

• Начальник пожарной части Зам начальника пожарной части Старшина части.docx

• Законе рф О защите прав потребителей.docx

• Тема Функции и методы, структура и документы стандартизации.docx