Файл: Разработка программного обеспечения алгоритма Диффи Хелмана на основе эллиптических кривых.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 295
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Часть 1: эллиптические кривые над вещественными числами и групповой закон
Групповой закон для эллиптических кривых
Часть 2: эллиптические кривые над конечными полями и задача дискретного логарифмирования
Порядок группы эллиптической кривой
Скалярное умножение и циклические подгруппы
Криптография на эллиптических кривых
Часть 4: алгоритмы для взлома защиты ECC и сравнение с RSA
Взлом задачи дискретного логарифмирования
Криптография на эллиптических кривых
Мы потратили много времени, но наконец добрались! Всё просто:
-
Закрытый ключ — это случайное целое , выбранное из
, выбранное из  (где
(где  — порядок подгруппы).
— порядок подгруппы). -
Открытый ключ — это точка (где
(где  — базовая точка подгруппы).
— базовая точка подгруппы).
Видите? Если мы знаем
 и
и  (вместе с другими параметрами области определения), то найти
(вместе с другими параметрами области определения), то найти  «просто». Но если мы знаем
«просто». Но если мы знаем  и
и  , то поиск закрытого ключа
, то поиск закрытого ключа  является «сложной» задачей, потому что требует решения задачи дискретного логарифмирования.
является «сложной» задачей, потому что требует решения задачи дискретного логарифмирования.Теперь мы опишем два основанных на этом принципе алгоритма с открытым ключом: ECDH (Elliptic curve Diffie-Hellman, протокол Диффи-Хеллмана на эллиптических кривых), используемый для шифрования, и ECDSA (Elliptic Curve Digital Signature Algorithm), используемый для цифровых подписей.
Шифрование с помощью ECDH
ECDH — это разновидность алгоритма Диффи-Хеллмана для эллиптических кривых. На самом деле это скорее протокол согласования ключей, а не алгоритм шифрования. В сущности, это означает, что ECDH задаёт (в определённой степени) порядок генерирования ключей и обмена ими. Способ шифрования данных с помощью таких ключей мы можем выбирать сами.
Он решает следующую проблему: две стороны (обычно Алиса и Боб) хотят безопасно обмениваться информацией, чтобы третья сторона (посредник, Man In the Middle) мог перехватывать её, но не мог расшифровать. Например, это один из принципов TLS.
Вот как это работает:
-
Сначала Алиса и Боб генерируют собственные закрытые и открытые ключи. У Алисы есть закрытый ключ и открытый ключ
и открытый ключ  , у Боба есть ключи
, у Боба есть ключи  и
и  . Заметьте, что и Алиса, и Боб используют одинаковые параметры области определения: одну базовую точку
. Заметьте, что и Алиса, и Боб используют одинаковые параметры области определения: одну базовую точку  на одной эллиптической кривой в одинаковом конечном поле.
на одной эллиптической кривой в одинаковом конечном поле. -
Алиса и Боб обмениваются открытыми ключами и
и  по незащищённому каналу. Посредник (Man In the Middle) перехватывает
по незащищённому каналу. Посредник (Man In the Middle) перехватывает  и
и  , но не может определить ни
, но не может определить ни  , ни
, ни  , не решив задачу дискретного логарифмирования.
, не решив задачу дискретного логарифмирования. -
Алиса вычисляет (с помощью собственного закрытого ключа и открытого ключа Боба), а Боб вычисляет
(с помощью собственного закрытого ключа и открытого ключа Боба), а Боб вычисляет  (с помощью собственного закрытого ключа и открытого ключа Алисы). Учтите, что
(с помощью собственного закрытого ключа и открытого ключа Алисы). Учтите, что  одинаков и для Алисы, и для Боба. На самом деле:
одинаков и для Алисы, и для Боба. На самом деле:

Однако посреднику известны только
 и
и  (вместе с другими параметрами области определения) и он не сможет найти общий секретный ключ
(вместе с другими параметрами области определения) и он не сможет найти общий секретный ключ  . Это известно как задача Диффи-Хеллмана, которую можно сформулировать следующим образом:
. Это известно как задача Диффи-Хеллмана, которую можно сформулировать следующим образом:Каким будет результат
 для трёх точек
для трёх точек  ,
,  и
и  ?
?Или, аналогично:
Каким будет результат
 для трёх целых
для трёх целых  ,
,  и
и  ?
?(Последняя формулировка используется в исходном алгоритме Диффи-Хеллмана, основанном на модулярной арифметике.)
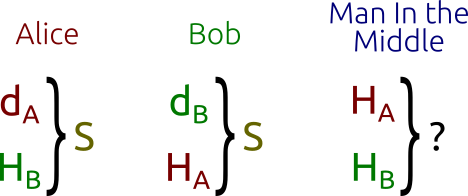
Протокол Диффи-Хеллмана: Алиса и Боб могут «просто» вычислить общий секретный ключ, посреднику же придётся решать «сложную» задачу.
Принцип, лежащий в основе задачи Диффи-Хеллмана, также объяснён в отличном видео Академии Хана на YouTube, в котором чуть позже объясняется алгоритм Диффи-Хеллмана в приложении к модулярной арифметике (не к эллиптическим кривым).
Задача Диффи-Хеллмана для эллиптических кривых считается «сложной». Считается, что она так же «сложна», как задача дискретного логарифмирования, но математических доказательств этому нет. Мы можем только с уверенностью сказать, что она не может быть «сложнее», потому что решение задачи логарифмирования — это способ решения задачи Диффи-Хеллмана.
Получив общий секретный ключ, Алиса и Боб могут обмениваться данными с симметричным шифрованием.
Например, они могут использовать координату
 ключа
ключа  как ключ для шифрования сообщений такими безопасными шифрами, как
как ключ для шифрования сообщений такими безопасными шифрами, как
AES или 3DES. Примерно это и делает TLS, разница в том, что TLS соединяет координату
 с другими числами, относящимися к подключению, а затем вычисляет хеш получившейся строки байтов.
с другими числами, относящимися к подключению, а затем вычисляет хеш получившейся строки байтов.Эксперименты с ECDH
Я написал ещё один скрипт на Python для вычисления закрытых/открытых ключей и общих секретных ключей над эллиптической кривой.
В отличие от показанных ранее примеров, в этом скрипте используется стандартизированная кривая, а не простая кривая на небольшом поле. Я выбрал кривую secp256k1 группы SECG («Standards for Efficient Cryptography Group», основанной Certicom). Та же самая кривая используется в Bitcoin для цифровых подписей. Вот параметры области определения:
-
 = 0xffffffff ffffffff ffffffff ffffffff ffffffff ffffffff fffffffe fffffc2f
= 0xffffffff ffffffff ffffffff ffffffff ffffffff ffffffff fffffffe fffffc2f -
 = 0
= 0 -
 = 7
= 7 -
 = 0x79be667e f9dcbbac 55a06295 ce870b07 029bfcdb 2dce28d9 59f2815b 16f81798
= 0x79be667e f9dcbbac 55a06295 ce870b07 029bfcdb 2dce28d9 59f2815b 16f81798 -
 = 0x483ada77 26a3c465 5da4fbfc 0e1108a8 fd17b448 a6855419 9c47d08f fb10d4b8
= 0x483ada77 26a3c465 5da4fbfc 0e1108a8 fd17b448 a6855419 9c47d08f fb10d4b8 -
 = 0xffffffff ffffffff ffffffff fffffffe baaedce6 af48a03b bfd25e8c d0364141
= 0xffffffff ffffffff ffffffff fffffffe baaedce6 af48a03b bfd25e8c d0364141 -
 = 1
= 1
(Эти числа взяты из исходного кода OpenSSL.)
Разумеется, вы можете изменить скрипт и использовать другие кривые и параметры области определения, только обязательно используйте простые поля и обычную формулировку Вейерштрасса, иначе скрипт не будет работать.
Скрипт очень прост и содержит некоторые из описанных выше алгоритмов: сложение точек, удвоение-сложение, ECDH. Рекомендую изучить и запустить его. Он создаёт примерно такие выходные данные:
Curve: secp256k1
Alice's private key: 0xe32868331fa8ef0138de0de85478346aec5e3912b6029ae71691c384237a3eeb
Alice's public key: (0x86b1aa5120f079594348c67647679e7ac4c365b2c01330db782b0ba611c1d677, 0x5f4376a23eed633657a90f385ba21068ed7e29859a7fab09e953cc5b3e89beba)
Bob's private key: 0xcef147652aa90162e1fff9cf07f2605ea05529ca215a04350a98ecc24aa34342
Bob's public key: (0x4034127647bb7fdab7f1526c7d10be8b28174e2bba35b06ffd8a26fc2c20134a, 0x9e773199edc1ea792b150270ea3317689286c9fe239dd5b9c5cfd9e81b4b632)
Shared secret: (0x3e2ffbc3aa8a2836c1689e55cd169ba638b58a3a18803fcf7de153525b28c3cd, 0x43ca148c92af58ebdb525542488a4fe6397809200fe8c61b41a105449507083)
Эфемерное ECDH
Некоторые из вас, возможно, слышали об ECDHE, а не об ECDH. «E» в ECHDE обозначает «Ephemeral» (эфемерное) и связано с тем, что передаваемые ключи временны, а не статичны.
ECDHE используется, например, в TLS, где клиент и сервер генерируют свою пару закрытого-открытого ключа на лету, при установке соединения. Затем ключи подписываются сертификатом TLS (для авторизации) и передаются между сторонами.
Подписывание с помощью ECDSA
Сценарий следующий: Алиса хочет подписать сообщение своим закрытым ключом (
 ), а Боб хочет проверить подпись с помощью открытого ключа Алисы (
), а Боб хочет проверить подпись с помощью открытого ключа Алисы ( ). Никто, кроме Алисы не должен иметь возможности создать действительные подписи. Каждый должен иметь возможность проверить подписи.
). Никто, кроме Алисы не должен иметь возможности создать действительные подписи. Каждый должен иметь возможность проверить подписи.Алиса и Боб снова используют одинаковые параметры области определения. Мы рассмотрим алгоритм ECDSA, разновидность Digital Signature Algorithm, применённого к эллиптическим кривым.
ECDSA работает с хешем сообщения, а не с самим сообщением. Выбор хеш-функции остаётся за нами, но, очевидно, нужно выбирать криптографическую хеш-функцию. Хеш сообщения необходимо урезать, чтобы битовая длина хеша была такой же, что и битовая длина
 (порядок подгруппы). Урезанный хеш — это целое число и оно будет обозначаться как
(порядок подгруппы). Урезанный хеш — это целое число и оно будет обозначаться как  .
.Алгоритм, выполняемый Алисой для подписывания сообщения, работает следующим образом:
-
Берём случайное целое , выбранное из
, выбранное из  (где
(где  — это по-прежнему порядок группы).
— это по-прежнему порядок группы). -
Вычисляем точку (где
(где  — базовая точка подгруппы).
— базовая точка подгруппы). -
Вычисляем число (где
(где  — это координата
— это координата 
 ).
). -
Если , то выбираем другое
, то выбираем другое  и пробуем снова.
и пробуем снова. -
Вычисляем (где
(где  — закрытый ключ Алисы, а
— закрытый ключ Алисы, а  — мультипликативная инверсия
— мультипликативная инверсия  по модулю
по модулю  ).
). -
Если , то выбираем другое
, то выбираем другое  и пробуем снова.
и пробуем снова.
Пара
 является подписью.
является подписью.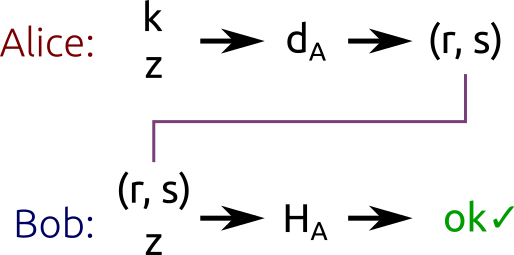
Алиса подписывает хеш
 с помощью закрытого ключа
с помощью закрытого ключа  и случайного
и случайного  . Боб проверяет правильность подписи сообщения с помощью открытого ключа Алисы
. Боб проверяет правильность подписи сообщения с помощью открытого ключа Алисы  .
.Проще говоря, этот алгоритм сначала генерирует секретный ключ (
 ). Благодаря умножению точек (которое, как мы знаем, является «простым» в одну сторону и «сложным» в обратную) секретный ключ прячется в
). Благодаря умножению точек (которое, как мы знаем, является «простым» в одну сторону и «сложным» в обратную) секретный ключ прячется в  . Затем
. Затем  привязывается к хешу сообщения уравнением
привязывается к хешу сообщения уравнением  .
.Учтите, что для вычисления
 мы вычислили обратную величину
мы вычислили обратную величину  по модулю
по модулю  . Как было сказано в предыдущей части, это гарантировано сработает только если
. Как было сказано в предыдущей части, это гарантировано сработает только если  — простое число. Если подгруппа имеет порядок непростого числа, ECDSA использовать не удастся. Неслучайно все стандартизированные кривые имеют простой порядок, а имеющие непростой порядок неприменимы для ECDSA.
— простое число. Если подгруппа имеет порядок непростого числа, ECDSA использовать не удастся. Неслучайно все стандартизированные кривые имеют простой порядок, а имеющие непростой порядок неприменимы для ECDSA.Проверка подписей
Для проверки подписи необходим открытый ключ Алисы
 , (урезанный) хеш
, (урезанный) хеш  и, очевидно, подпись
и, очевидно, подпись  .
.-
Вычисляем целое .
. -
Вычисляем целое .
. -
Вычисляем точку .
.
Подпись действительна, только если
 .
.