ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 397
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Fи F',
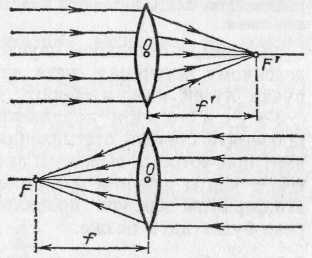
Рис. 196. Фокусы линзы
а всегда более или менее расплывчатое светлое пятнышко.
Другое обстоятельство, которое нужно помнить, состоит в том, что мы не можем осуществить строго точечный источник света. Поэтому, поместив в фокусе линзы источник хотя бы очень малых, но всегда конечных размеров, мы не получим с помощью линзы строго параллельный пучок лучей.
В § 70 было указано, что строго параллельный пучок лучей не имеет физического смысла. Сделанное замечание показывает, что рассмотренные свойства линзы находятся в согласии с этим общим физическим положением.
В каждом отдельном случае применения линзы к определенному источнику света для получения параллельного пучка лучей или, наоборот, при применении линзы для фокусировки параллельного пучка надо специально проверять степень отступления от тех упрощающих условий, при которых выведены формулы. Но существенные черты явления преломления световых лучей в линзе эти формулы передают правильно, а об отступлениях от них речь будет идти позже.
41. Формула линзы. Действительное и мнимое изображение.
Изображение в линзе точек, лежащих на главной оптической оси. Формула линзы. Пусть точечный источник света находится в точке S на главной оптической оси линзы, на расстоянии а от ее оптического центра О (рис. 197). Рассмотрим, как будет преломляться в линзе узкий пучок лучей, примыкающий к прямой SO, являющейся осью этого пучка *).
Пусть один из лучей (SM) светового пучка падает на первую преломляющую поверхность линзы в точке М, находящейся на высоте hнад осью. То обстоятельство, что мы ограничиваемся узким пучком лучей, означает, что hмало по сравнению с расстоянием а от источника до линзы. С другой стороны, так же как и в § 88, будем считать, что hмало по сравнению с f', а следовательно, и по сравнению с радиусами R1и R2 ограничивающих линзу поверхностей. Угол, образуемый лучом SMс осью, обозначим . Так как hмало, то и угол мал. Преломленный луч пойдет по направлению ММ' и, преломившись снова на второй ограничивающей линзу поверхности, выйдет из линзы по направлению M'S',
составляющему с осью угол '. Обозначим через а' расстояние от оптического центра линзы до точки S', в которой преломленный луч пересекает главную ось.
*) Такие пучки обычно называют параксиальными (приосевыми).
Как и в предыдущем параграфе, проведем через точки М и М' плоскости, касательные к преломляющим поверхностям линзы. Эти плоскости образуют тонкую призму ВАВ' с преломляющим углом . Вместо того чтобы рассматривать преломление луча SMM'S' в линзе, будем рассматривать преломление того же луча в тонкой призме ВАВ'.
Выбранный нами луч после преломления отклонится от первоначального направления на угол а, который по формуле тонкой призмы равен
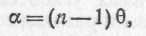(89.1)
где n— показатель преломления вещества, из которого сделана линза.
Рассмотрим также луч РМ, идущий параллельно главной оси и падающий на линзу в точке М. Преломление такого луча уже рассмотрено в § 88 (условие малости hздесь соблюдено). Мы знаем, что после преломления в линзе этот луч выйдет из точки М" под углом к оси и пройдет через главный фокус F' на расстоянии f' от оптического центра.
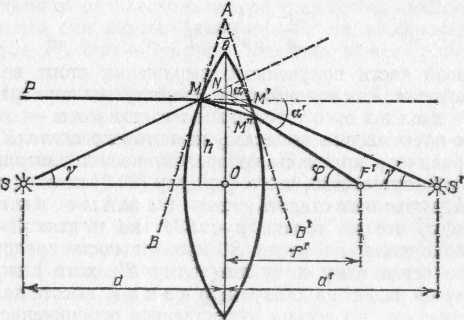
Рис. 197. Преломление в линзе луча SM, выходящего из точки S на оси. Угол ВАВ' и толщина линзы сильно преувеличены
Точки М' и М" очень близки друг к другу, так что призмы, образованные касательными в точке М и точках М' или М", практически не различаются и имеют один и тот же преломляющий угол . Угол ', на который отклонится этот луч от первоначального направления после преломления в тонкой призме, равен опять (n—1), т. е. равен углу . С другой стороны, этот угол ' равен, очевидно, углу (рис. 197).
Таким образом, получаем
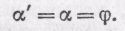(89.2)
Но угол а как внешний угол в треугольнике SNS' равен сумме +'. Итак, имеем
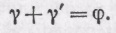(89.3)
Лучи SM, M'S' и M"F' идут под небольшими углами к оси, т. е. углы , 'и малы. Заменяя, как и в предыдущем параграфе, синусы малых углов самими углами и пренебрегая толщиной линзы и разницей в высоте точек
М, М' и М" над осью, можно приближенно написать:
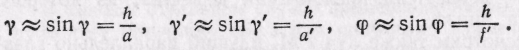(89.4)
Подставляя эти приближенные равенства в формулу (89.3), находим
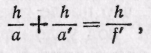(89.5)
или, сокращая на общий множитель h,
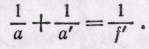(89.6)
В правой части полученного выражения стоит величина 1/f', которая, как мы видели в предыдущем параграфе, зависит только от свойств линзы — от показателя преломления вещества, из которого сделана линза, и от радиусов кривизны ее преломляющих поверхностей.
То обстоятельство, что в формулу (89.6) не входит величина h, позволяет сделать очень важные выводы, а именно, что не только луч SM, но и всякий другой луч, выходящий из точки S, пройдет после преломления в линзе через одну и ту же точку S', хотя каждый из этих лучей падает на линзу на разной высоте над осью. Единственное, но весьма существенное ограничение, которое мы накладываем на рассматриваемые лучи, состоит в том, что все они составляют с осью линзы малые углы.
Таким образом, все лучи узкого пучка, выходящие из точки S, соберутся после преломления в линзе снова в одной точке S', являющейся изображением точки S. Мы доказали, следовательно, что образующееся в тонкой линзе изображение точечного источника, лежащего на главной оси линзы, полученное с помощью достаточно узкого пучка лучей, является точкой.
Изображения, при получении которых выполнено условие передачи каждой точки объекта одной точкой изображения, носят название стигматических. Изображения, у которых это условие не соблюдено, носят название астигматических *).
Отметим, что в силу закона обратимости световых лучей (§ 82) положения источника света Sи его изображения S' обратимы, т. е., поместив источник в S', мы получим его изображение в точке S. Точки S и S' называются сопряженными.
В геометрической оптике особое значение имеет задача получения стигматических изображений. Степень стигматичности изображений определяет качество служащих для их получения оптических систем. Нарушение оптической системой стигматичности падающих на нее световых пучков ведет к расплывчатости изображения. В дальнейшем при изучении простейших оптических систем мы будем уделять большое внимание вопросу о стигматичности даваемых ими изображений.
Полученная нами формула (89.6) связывает между собой расстояния от оптического центра трех точек, находящихся на главной оси линзы: источника S, его изображения S' и фокуса F'. Это — основная формула тонкой линзы.
§ 90. Применения формулы тонкой линзы. Действительные и мнимые изображения. Предположим, что светящаяся точка S, лежащая на главной оси линзы, удаляется от линзы на очень большое расстояние. В этом случае лучи, падающие на линзу, будут стремиться стать параллельными ее главной оси. Мы видели в §88, что после преломления в линзе эти лучи соберутся в фокусе F' линзы. В формуле (89.6) при удалении источника на очень большое расстояние величина На стремится к нулю, и мы получаем
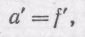
т. е. можно сказать, что фокус F' есть изображение «бесконечно удаленной» точки.
Примером практически бесконечно удаленного источника может служить любое небесное тело. Следовательно, изображения звезд, Солнца и т. д. будут находиться в фокусе линзы. Достаточно далекие от линзы земные источники света также дают изображение в ее фокусе.
*) Стигма значит по-гречески точка, стигматический — точечный, частица «а» впереди слова — знак отрицания. Астигматический значит неточечный
Предположим теперь, что изображение некоторой точки удалено на очень большое расстояние, т. е. из линзы выходит пучок световых лучей, параллельных главной оси. В этом случае, как мы видели в § 88, источник должен находиться в переднем фокусе линзы F(рис. 196). Этот вывод следует и из формулы (89.6). Действительно, полагая, что изображение находится в бесконечности, получаем 1/а'=0; при этом расстояние источника от линзы равно фокусному расстоянию: а=f=f'.
Различные линзы отличаются одна от другой расположением центров образующих их сферических поверхностей,
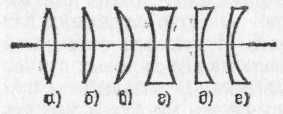
Рис. 198. Различные типы линз. Если материал линз преломляет сильнее, чем окружающая среда, то типы а, б, в — собирающие; типы г, д, е — рассеивающие
их радиусами и показателями преломления вещества, из которого сделаны линзы. На рис. 198 представлены шесть основных типов линз.
Если параллельные лучи после преломления в линзе сходятся, действительно пересекаясь в некоторой точке, лежащей по другую сторону линзы, то линза называется
Рис. 196. Фокусы линзы
а всегда более или менее расплывчатое светлое пятнышко.
Другое обстоятельство, которое нужно помнить, состоит в том, что мы не можем осуществить строго точечный источник света. Поэтому, поместив в фокусе линзы источник хотя бы очень малых, но всегда конечных размеров, мы не получим с помощью линзы строго параллельный пучок лучей.
В § 70 было указано, что строго параллельный пучок лучей не имеет физического смысла. Сделанное замечание показывает, что рассмотренные свойства линзы находятся в согласии с этим общим физическим положением.
В каждом отдельном случае применения линзы к определенному источнику света для получения параллельного пучка лучей или, наоборот, при применении линзы для фокусировки параллельного пучка надо специально проверять степень отступления от тех упрощающих условий, при которых выведены формулы. Но существенные черты явления преломления световых лучей в линзе эти формулы передают правильно, а об отступлениях от них речь будет идти позже.
41. Формула линзы. Действительное и мнимое изображение.
Изображение в линзе точек, лежащих на главной оптической оси. Формула линзы. Пусть точечный источник света находится в точке S на главной оптической оси линзы, на расстоянии а от ее оптического центра О (рис. 197). Рассмотрим, как будет преломляться в линзе узкий пучок лучей, примыкающий к прямой SO, являющейся осью этого пучка *).
Пусть один из лучей (SM) светового пучка падает на первую преломляющую поверхность линзы в точке М, находящейся на высоте hнад осью. То обстоятельство, что мы ограничиваемся узким пучком лучей, означает, что hмало по сравнению с расстоянием а от источника до линзы. С другой стороны, так же как и в § 88, будем считать, что hмало по сравнению с f', а следовательно, и по сравнению с радиусами R1и R2 ограничивающих линзу поверхностей. Угол, образуемый лучом SMс осью, обозначим . Так как hмало, то и угол мал. Преломленный луч пойдет по направлению ММ' и, преломившись снова на второй ограничивающей линзу поверхности, выйдет из линзы по направлению M'S',
составляющему с осью угол '. Обозначим через а' расстояние от оптического центра линзы до точки S', в которой преломленный луч пересекает главную ось.
*) Такие пучки обычно называют параксиальными (приосевыми).
Как и в предыдущем параграфе, проведем через точки М и М' плоскости, касательные к преломляющим поверхностям линзы. Эти плоскости образуют тонкую призму ВАВ' с преломляющим углом . Вместо того чтобы рассматривать преломление луча SMM'S' в линзе, будем рассматривать преломление того же луча в тонкой призме ВАВ'.
Выбранный нами луч после преломления отклонится от первоначального направления на угол а, который по формуле тонкой призмы равен
(89.1)где n— показатель преломления вещества, из которого сделана линза.
Рассмотрим также луч РМ, идущий параллельно главной оси и падающий на линзу в точке М. Преломление такого луча уже рассмотрено в § 88 (условие малости hздесь соблюдено). Мы знаем, что после преломления в линзе этот луч выйдет из точки М" под углом к оси и пройдет через главный фокус F' на расстоянии f' от оптического центра.
Рис. 197. Преломление в линзе луча SM, выходящего из точки S на оси. Угол ВАВ' и толщина линзы сильно преувеличены
Точки М' и М" очень близки друг к другу, так что призмы, образованные касательными в точке М и точках М' или М", практически не различаются и имеют один и тот же преломляющий угол . Угол ', на который отклонится этот луч от первоначального направления после преломления в тонкой призме, равен опять (n—1), т. е. равен углу . С другой стороны, этот угол ' равен, очевидно, углу (рис. 197).
Таким образом, получаем
(89.2)Но угол а как внешний угол в треугольнике SNS' равен сумме +'. Итак, имеем
(89.3)Лучи SM, M'S' и M"F' идут под небольшими углами к оси, т. е. углы , 'и малы. Заменяя, как и в предыдущем параграфе, синусы малых углов самими углами и пренебрегая толщиной линзы и разницей в высоте точек
М, М' и М" над осью, можно приближенно написать:
(89.4)Подставляя эти приближенные равенства в формулу (89.3), находим
(89.5)или, сокращая на общий множитель h,
(89.6)В правой части полученного выражения стоит величина 1/f', которая, как мы видели в предыдущем параграфе, зависит только от свойств линзы — от показателя преломления вещества, из которого сделана линза, и от радиусов кривизны ее преломляющих поверхностей.
То обстоятельство, что в формулу (89.6) не входит величина h, позволяет сделать очень важные выводы, а именно, что не только луч SM, но и всякий другой луч, выходящий из точки S, пройдет после преломления в линзе через одну и ту же точку S', хотя каждый из этих лучей падает на линзу на разной высоте над осью. Единственное, но весьма существенное ограничение, которое мы накладываем на рассматриваемые лучи, состоит в том, что все они составляют с осью линзы малые углы.
Таким образом, все лучи узкого пучка, выходящие из точки S, соберутся после преломления в линзе снова в одной точке S', являющейся изображением точки S. Мы доказали, следовательно, что образующееся в тонкой линзе изображение точечного источника, лежащего на главной оси линзы, полученное с помощью достаточно узкого пучка лучей, является точкой.
Изображения, при получении которых выполнено условие передачи каждой точки объекта одной точкой изображения, носят название стигматических. Изображения, у которых это условие не соблюдено, носят название астигматических *).
Отметим, что в силу закона обратимости световых лучей (§ 82) положения источника света Sи его изображения S' обратимы, т. е., поместив источник в S', мы получим его изображение в точке S. Точки S и S' называются сопряженными.
В геометрической оптике особое значение имеет задача получения стигматических изображений. Степень стигматичности изображений определяет качество служащих для их получения оптических систем. Нарушение оптической системой стигматичности падающих на нее световых пучков ведет к расплывчатости изображения. В дальнейшем при изучении простейших оптических систем мы будем уделять большое внимание вопросу о стигматичности даваемых ими изображений.
Полученная нами формула (89.6) связывает между собой расстояния от оптического центра трех точек, находящихся на главной оси линзы: источника S, его изображения S' и фокуса F'. Это — основная формула тонкой линзы.
§ 90. Применения формулы тонкой линзы. Действительные и мнимые изображения. Предположим, что светящаяся точка S, лежащая на главной оси линзы, удаляется от линзы на очень большое расстояние. В этом случае лучи, падающие на линзу, будут стремиться стать параллельными ее главной оси. Мы видели в §88, что после преломления в линзе эти лучи соберутся в фокусе F' линзы. В формуле (89.6) при удалении источника на очень большое расстояние величина На стремится к нулю, и мы получаем
т. е. можно сказать, что фокус F' есть изображение «бесконечно удаленной» точки.
Примером практически бесконечно удаленного источника может служить любое небесное тело. Следовательно, изображения звезд, Солнца и т. д. будут находиться в фокусе линзы. Достаточно далекие от линзы земные источники света также дают изображение в ее фокусе.
*) Стигма значит по-гречески точка, стигматический — точечный, частица «а» впереди слова — знак отрицания. Астигматический значит неточечный
Предположим теперь, что изображение некоторой точки удалено на очень большое расстояние, т. е. из линзы выходит пучок световых лучей, параллельных главной оси. В этом случае, как мы видели в § 88, источник должен находиться в переднем фокусе линзы F(рис. 196). Этот вывод следует и из формулы (89.6). Действительно, полагая, что изображение находится в бесконечности, получаем 1/а'=0; при этом расстояние источника от линзы равно фокусному расстоянию: а=f=f'.
Различные линзы отличаются одна от другой расположением центров образующих их сферических поверхностей,
Рис. 198. Различные типы линз. Если материал линз преломляет сильнее, чем окружающая среда, то типы а, б, в — собирающие; типы г, д, е — рассеивающие
их радиусами и показателями преломления вещества, из которого сделаны линзы. На рис. 198 представлены шесть основных типов линз.
Если параллельные лучи после преломления в линзе сходятся, действительно пересекаясь в некоторой точке, лежащей по другую сторону линзы, то линза называется