Файл: Сборник работ для суммативного оценивания по алгебре и началам анализа 11 класс.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 4590
Скачиваний: 247
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «СТЕПЕНИ И КОРНИ. СТЕПЕННАЯ ФУНКЦИЯ»
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»
ВАРИАНТ 1
1. Дан металлический шар радиусом 12 см.
а) Найдите объем данного шара.
b) Этот шар положили в цилиндрический контейнер радиусом 25 см и высотой 60 см.
После этого контейнер наполнили водой.
Рассчитайте объем воды, потребовавшейся для наполнения контейнера
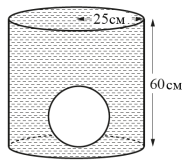
c)Затем шар достали из контейнера. Какова глубина воды, оставшейся в контейнере?
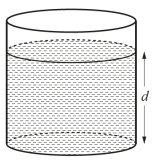
d) Металлический шар переплавили в конус высотой 52 см. Найдите радиус конуса.
(Ответ округлите до десятых)
2. SABC - пирамида. SA
(ABC), SA = 4 √3 см, BC = 8 см , двугранный угол при ребреBC равен 450 . Выполнив рисунок, вычислите объем пирамиды.
3. Объем шара равен 36
. Найдите площадь сферы, ограничивающей данный шар. (При необходимисти значения округлять до целых) 4. В прямой призме, основанием которой является прямоугольный треугольник, пять ребер равны 6, а остальные четыре ребра равны друг другу.
Выполните рисунок и найдите объем призмы.
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ 1 ВАРИАНТ
| № | Ответ | Балл | Дополнительная информация |
| 1 a | 2403π (см3) | 1 | |
| 1 b | 252 *60π-2403π | 1 | |
| 35097π(см3) | 1 | | |
| 1 c | 35097π/252 π | 1 | |
| 56,1552 (см) | 1 | | |
| 1d | 1/3πr2*52=2403 | 1 | |
| r≈6.13 | 1 | | |
| 2 | Выполнен рисунок по условию задачи | 1 | |
| Высота треугольника АВС, проведенная к стороне BC= 4 √3 | 1 | | |
| V=1/3*1/2*8*4 √3 *4 √3 | 1 | | |
| V=64(см)3 | 1 | | |
| 3 | V = (4/3) * π * R3 | 1 | |
| (4/3) * π * R3 = 36 * π см3 R3 = (36 * π ) : ((4/3) * π) = 27 см3. | 1 | | |
| R = 3 см. | 1 | | |
| S = 4 * π * R2 | 1 | | |
| S= 4 * π * 32 = 4 * π * 9 = 36 * π см2 | 1 | | |
| 4 | Выполнен рисунок по условию задачи и показаны соответствующие ребра | 1 | |
| Катет треугольника в основании 3√ 2 | 1 | | |
| V=1/2*6*3√2*3√2 | 1 | | |
| V=54(см)3 | 1 | | |
| Итого: | 20 | | |
ВАРИАНТ 2
| Разбаловка заданий работы | ||||
| № задания | 1 | 2 | 3 | 4 |
| Количество баллов | 7 | 4 | 5 | 4 |
| итого | 20 баллов | |||
1 ... 51 52 53 54 55 56 57 58 59
1. Дан металлический шар радиусом 9 см.
а) Найдите объем данного шара.
b) Этот шар положили в цилиндрический контейнер радиусом 25 см и высотой 60 см.
После этого контейнер наполнили водой.
Рассчитайте объем воды, потребовавшейся для наполнения контейнера
c)Затем шар достали из контейнера. Какова глубина воды, оставшейся в контейнере?
d) Металлический шар переплавили в конус высотой 27 см. Найдите радиус конуса.
(Ответ округлите до десятых)
2. SABC - пирамида. SA
(ABC), SA = 4 √6 см, BC = 8 см , двугранный угол при ребреBC равен 450 . Выполнив рисунок, вычислите объем пирамиды.
3. Объем шара равен 64
. Найдите площадь сферы, ограничивающей данный шар.(При необходимисти значения округлять до целых) 4. В прямой призме, основанием которой является прямоугольный треугольник, пять ребер равны 4, а остальные четыре ребра равны друг другу.
Выполните рисунок и найдите объем призмы.
Схема выставления баллов 2 вариант
| № | Ответ | Балл | Дополнительная информация |
| 1 a | 972π (см3) | 1 | |
| 1 b | 252 *60π-972π | 1 | |
| 36528π(см3) | 1 | | |
| 1 c | 36528π/252 π | 1 | |
| 58,4448 (см) | 1 | | |
| 1d | 1/3πr2*27=972 | 1 | |
| r≈5,73 | 1 | | |
| 2 | Выполнен рисунок по условию задачи | 1 | |
| Высота треугольника АВС, проведенная к стороне BC= 4 √6 | 1 | | |
| V=1/3*1/2*8*4 √6 *4 √6 | 1 | | |
| V=128(см)3 | 1 | | |
| 3 | V = (4/3) * π * R3 | 1 | |
| (4/3) * π * R3 = 64 * π см3 R3 = (64 * π ) : ((4/3) * π) = 48 см3. | 1 | | |
| R ≈4 см. | 1 | | |
| S = 4 * π * R2 | 1 | | |
| S= 4 * π * 42 = 4 * π * 16 = 64 * π см2 | 1 | | |
| 4 | Выполнен рисунок по условию задачи и показаны соответствующие ребра | 1 | |
| | Катет треугольника в основании 2√ 2 | 1 | |
| | V=1/2*4*2√2*2√2 | 1 | |
| | V=16(см)3 | 1 | |
| Итого: | 20 | | |
ВАРИАНТ 3
| Разбаловка заданий работы | ||||
| № задания | 1 | 2 | 3 | 4 |
| Количество баллов | 7 | 4 | 5 | 4 |
| итого | 20 баллов | |||
1 ... 51 52 53 54 55 56 57 58 59
1. Дан металлический шар радиусом 9 см.
а) Найдите объем данного шара.
b) Этот шар положили в цилиндрический контейнер радиусом 25 см и высотой 60 см.
После этого контейнер наполнили водой.
Рассчитайте объем воды, потребовавшейся для наполнения контейнера
c)Затем шар достали из контейнера. Какова глубина воды, оставшейся в контейнере?
d) Металлический шар переплавили в конус высотой 30 см. Найдите радиус конуса.
(Ответ округлите до десятых)
2. SABC - пирамида. SA
(ABC), SA = 4 √6 см, BC = 8 см , двугранный угол при ребре BC равен 450 . Выполнив рисунок, вычислите объем пирамиды.3. Объем шара равен 64
. Найдите площадь сферы, ограничивающей данный шар.(При необходимисти значения округлять до целых) 4. В прямой призме, основанием которой является прямоугольный треугольник, пять ребер равны 8, а остальные четыре ребра равны друг другу.
Выполните рисунок и найдите объем призмы.
Схема выставления баллов 3 вариант
| № | Ответ | Балл | Дополнительная информация |
| 1 a | 972π (см3) | 1 | |
| 1 b | 252 *60π-972π | 1 | |
| 36528π(см3) | 1 | | |
| 1 c | 36528π/252 π | 1 | |
| 58,4448 (см) | 1 | | |
| 1d | 1/3πr2*30=972 | 1 | |
| r≈5,76 | 1 | | |
| 2 | Выполнен рисунок по условию задачи | 1 | |
| Высота треугольника АВС, проведенная к стороне BC= 4 √6 | 1 | | |
| V=1/3*1/2*8*4 √6 *4 √6 | 1 | | |
| V=128(см)3 | 1 | | |
| 3 | V = (4/3) * π * R3 | 1 | |
| (4/3) * π * R3 = 64 * π см3 R3 = (64 * π ) : ((4/3) * π) = 48 см3. | 1 | | |
| R ≈4 см. | 1 | | |
| S = 4 * π * R2 | 1 | | |
| S= 4 * π * 42 = 4 * π * 16 = 64 * π см2 | 1 | | |
| 4 | Выполнен рисунок по условию задачи и показаны соответствующие ребра | 1 | |
| | Катет треугольника в основании 4√ 2 | 1 | |
| | V=1/2*8*4√2*4√2 | 1 | |
| | V=128(см)3 | 1 | |
| Итого: | 20 | | |