Файл: Сборник работ для суммативного оценивания по алгебре и началам анализа 11 класс.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 4593
Скачиваний: 247
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «СТЕПЕНИ И КОРНИ. СТЕПЕННАЯ ФУНКЦИЯ»
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»


ФИ УЧАЩЕГОСЯ________________________________________
| Критерий оценивания | Уровень учебных достижений | ||
| Низкий | Средний | Высокий | |
| Определяет область допустимых значений иррационального уравнения | Затрудняется в определении области допустимых значений иррационального уравнения | Записывает систему неравенств для нахождения области допустимых значений иррационального уравнения, но допускает ошибки при их решении | Находит область допустимых значений иррационального уравнения |
| Решает иррациональное уравнение методом возведения обеих частей уравнения в n-ую степень | Затрудняется в решении иррационального уравнения методом возведения обеих частей уравнения в n-ую степень | Возводит обе части уравнения в n-ую степень, но допускает ошибки при его решении | Решает иррациональное уравнение методом возведения обеих частей уравнения в n-ую степень |
| Решает иррациональное уравнение методом замены переменной | Затрудняется в применении метода замены переменной при решении иррационального уравнения | Применяет метод замены переменной при решении иррационального уравнения, но допускает ошибки в решении полученного уравнения или в решении уравнения при возврате к исходной переменной | Решает иррациональное уравнение методом замены переменной. |
| Решает иррациональное неравенство | Затрудняется в решении иррационального неравенства | Допускает ошибки при нахождении решений равносильной системы неравенств | Решает иррациональное неравенство |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «КОМПЛЕКСНЫЕ ЧИСЛА»
| Тема | Мнимые числа. Определение комплексных чисел. Действия над комплексными числами в алгебраической форме. Комплексные корни квадратных уравнений. Основная теорема алгебры. |
| Цель обучения | 11.1.1.1 Знать определение комплексного числа и его модуля 11.1.1.2 Уметь изображать комплексное число на комплексной плоскости 11.1.1.3 Знать определение сопряженных комплексных чисел и их свойства 11.1.2.1 Выполнять арифметические действия над комплексными числами в алгебраической форме 11.1.2.3 Уметь извлекать квадратный корень из комплексного числа 11.1.2.4 Решать квадратные уравнения на множестве комплексных чисел |
| Критерий оценивания | Обучающийся Определяет модуль комплексного числа Изображает комплексное число на комплексной плоскости Выполняет арифметические действия над комплексными числами в алгебраической форме Решает квадратные уравнения на множестве комплексных чисел Извлекает квадратный корень из комплексного числа |
| Уровень мыслительных навыков | Знание и понимание Применение |
| Время выполнения | 30 минут |
ЗАДАНИЯ
| Оценивание заданий работы | ||||||
| № задания | 1 | 2 | 3 | 4 | 5 | 6 |
| Количество баллов | 3 | 2 | 3 | 4 | 2 | 5 |
| Всего баллов | 19 баллов | |||||
1 ВАРИАНТ
-
Изобразите на плоскости заданные комплексные числа:
Z1 = 4i
Z2 = 3 + i
2. Найдите сопряженное число комплексного числа и вычислите его модуль :.
Z = 3 + 4i
3. Выполните действие над комплексными числами
а) (3 + 5i)2,
б)
4. Найдите действительные числа x и y так, чтобы выполнялось равенства:
(x-3i)(2+i)=x+yi
5. Решите уравнения:
x2 – 4x + 13 = 0.
6. Извлеките квадратный корень из числа z = -7+24i
2 ВАРИАНТ
-
Изобразите на плоскости заданные комплексные числа:
Z1= -5i
Z2= 4 + i
2 .Найдите сопряженное число комплексного числа и вычислите его модуль :
Z = 8 + 4i
3. Выполните действие над комплексными числами
а)(2 – 7i)2,
б)
4.Найдите действительные числа x и y так, чтобы выполнялось равенства:
(2+yi)(4-2i)=x-3yi
5.Решите уравнения:
х2 − 6х + 18 = 0.
6.Извлеките квадратный корень из числа
z = -5+i
3 ВАРИАНТ
1.Изобразите на плоскости заданные комплексные числа:
Z1=-3 -5i
Z2= 2 + i
2 .Найдите сопряженное число комплексного числа и вычислите его модуль :
Z = -3 + 3i
3. Выполните действие над комплексными числами
а) (4 + 3i)(4 – 3i),
б)
4.Найдите действительные числа x и y так, чтобы выполнялось равенства:
(2+yi)(4-2i)=x-3yi
5.Решите уравнения:
x2 + 3x + 4=0
6.Извлеките квадратный корень из числа
z = -125i
4 ВАРИАНТ
1.Изобразите на плоскости заданные комплексные числа:
Z1=-2 +6i
Z2= -4-2 i
2 .Найдите сопряженное число комплексного числа и вычислите его модуль :
Z = 2 - 3i
3. Выполните действие над комплексными числами
а) (6 + 4i)(5 + 2i)
б)
4.Найдите действительные числа x и y так, чтобы выполнялось равенства:
(1+3i)2-2y=4x+2xyi
5.Решите уравнения:
4x2 – 20x + 26 = 0
6.Извлеките квадратный корень из числа
z = 3-2i
| Критерий оценивания | № задания | Дескриптор | Балл |
| Обучающийся | |||
| Изображает комплексное число на комплексной плоскости | 1 | определяет на комплексной плоскости действительную часть комплексного числа; | 1 |
| определяет на комплексной плоскости мнимую часть комплексного числа; | 1 | ||
| изображает на комплексной плоскости число; | 1 | ||
| Определяет модуль комплексного числа | 2 | записывает комплексно – сопряженное число; | 1 |
| вычисляет модуль комплексного числа сопряженного числа | 1 | ||
| Выполняет арифметические действия над комплексными числами в алгебраической форме | 3 | Применяет формулу деления комплексных чисел; | 1 |
| умножает два комплексных числа; | 1 | ||
| Находит частное двух комплексных чисел; | 1 | ||
| 4 | возводит в степень комплексное число; | 1 | |
| раскрывает скобки и приводит подобные слагаемые; | 1 | ||
| составляет и решает систему уравнений; | 1 | ||
| находит значения x и y. | 1 | ||
| Решает квадратные уравнения на множестве комплексных чисел | 5 | вычисляет дискриминант; | 1 |
| находит комплексные корни уравнения; | 1 | ||
| Извлекает квадратный комплексного корень из числа | 6 | применяет метод извлечения квадратного корня из комплексного числа; | 1 |
| возводит обе части выражения в квадрат; | 1 | ||
| составляет и решает систему уравнений; | 1 | ||
| находит действительную и мнимую часть комплексного числа; | 1 | ||
| записывает ответ. | 1 | ||
| Итого: | 19 | ||
-
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ -
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ -
ЗА РАЗДЕЛ «КОМПЛЕКСНЫЕ ЧИСЛА»


ФИ УЧАЩЕГОСЯ ___________________________________________
| Критерий оценивания | Уровень учебных достижений | ||
| Низкий | Средний | Высокий | |
| Изображает комплексное число на комплексной плоскости | Затрудняется в изображении комплексного числа на комплексной плоскости | Допускает ошибки при изображении действительной/ мнимой части комплексного числа | Изображает комплексное число на комплексной плоскости |
| Определяет модуль комплексного числа | Затрудняется в нахождении модуля комплексного числа | Допускает ошибки при нахождении модуля комплексного числа | Находит модуль комплексного числа |
| Выполняет арифметические действия над комплексными числами в алгебраической форме | Затрудняется в выполнении арифметических действий над комплексными числами в алгебраической форме | Допускает ошибки при нахождении суммы/ умножения/ частного комплексных чисел. | Выполняет арифметические действия над комплексными числами в алгебраической форме |
| Решает квадратные уравнения на множестве комплексных чисел | Затрудняется в решении квадратных уравнений на множестве комплексных чисел | Допускает ошибки в решении квадратных уравнений на множестве комплексных чисел | Находит решение квадратных уравнений на множестве комплексных чисел |
| Извлекает квадратный корень из комплексного числа | Затрудняется в извлечении корня из комплексного числа. | Допускает ошибки в извлечении корня из комплексного числа. | Извлекает квадратный корень из комплексного числа |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ»
| Тема | Показательная функция, ее свойства и график. Логарифм числа и его свойства. Логарифмическая функция, ее свойства и график. Производная и интеграл показательной функции. Производная логарифмической функции. |
| Цели обучения | 11.4.1.14 Знать определение показательной функции и строить ее график 11.4.1.17 Знать свойства логарифмов и применять их для преобразования логарифмических выражений 11.4.1.18 Знать определение логарифмической функции и строить ее график 11.4.1.20 Находить производную и интеграл показательной функции 11.4.1.21 Находить производную логарифмической функции |
| Критерии оценивания | Обучающийся Строит график показательной функции; Применяет свойства логарифмов для преобразования логарифмических выражений; Применяет определение логарифмической функции при построении ее графика; Находит производные показательной и логарифмической функций; Находит интеграл показательной функции . |
| Уровень мыслительных навыков | Применение |
| Время выполнения | 30 минут |
ЗАДАНИЯ
| Оценивание заданий работы | ||||
| № задания | 1 | 2 | 3 | 4 |
| Количество баллов | 4 | 5 | 3 | 5 |
| Всего баллов | 17 баллов | |||
1 ВАРИАНТ
-
Постройте график функций:
а)
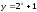 , б)
, б) 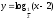
2.Найдите значение выражения :
3.Найдите производную функции :
4. Вычислите площадь фигуры, ограниченной линиями (ответ округлите до единиц):
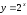 ,
, 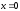 ,
, 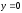 ,
,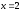 .
.2 ВАРИАНТ
1.Постройте график функций:
а)
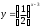 , б)
, б)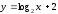
2.Найдите значение выражения