Файл: Сборник работ для суммативного оценивания по алгебре и началам анализа 11 класс.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 29.11.2023

Просмотров: 4689

Скачиваний: 247

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ

ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ

ЗА РАЗДЕЛ «СТЕПЕНИ И КОРНИ. СТЕПЕННАЯ ФУНКЦИЯ»

РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ

ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ

ЗА РАЗДЕЛ «ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»

СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ

Количество баллов – 25

Схема выставления баллов

Схема выставления баллов

Схема выставления баллов

Схема выставления баллов

СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ


Обзор суммативного оценивания за 2 четверть
Продолжительность – 40 минут

Количество баллов – 25


Типы заданий:

КО – задания, требующие краткого ответа;

РО – задания, требующие развернутого ответа.

  1. Структура суммативного оценивания


Данный вариант состоит из 6 заданий, включающих вопросы с кратким и развернутым ответами.

В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.

В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.

  1. Характеристика заданий суммативного оценивания за 2 четверть


Раздел
Проверяемая цель
Уровень мыслительных навыков
Кол.

заданий*
№

задания*
Тип

задания*
Время на выполнение, мин*
Балл*
Балл за

раздел



Степени и корни.

Степенная функция
11.2.1.3 - знать определение и свойства степени с рациональным показателем

11.4.1.13- знать и применять правила нахождения интеграла степенной функции с действительным показателем
Знание понимание


1
1 a


КО

3

1

16

Применение

1 b

2

11.4.1.11-знать свойства степенной

Функции

Знание и понимание
1
2
КО
5
2

11.2.1.5 - применять свойства корня n-ой степени для преобразования иррациональных выражений

11.4.1.12 - знать и применять правила нахождения производной степенной функции с действительным показателем
Применение


1


3
РО

7


5

11.2.1.2 - знать свойства корня n-ой степени

11.2.1.4 - применять свойства степени с рациональным показателем для преобразования алгебраических выражений
Знание и понимание


1


6
РО
10


6

Применение

Иррациональ ные

уравнения и неравенства
11.2.2.4-уметь решать системы

иррациональных уравнений
Применение
1
4
РО
10
6

9

11.2.2.5 - уметь решать иррациональные

неравенства
Применение
1
5
PO
5

3

ИТОГО:






6






40



25

Примечание: * - разделы, в которые можно вносить изменения


1 ВАРИАНТ


Оценивание заданий работы

№ задания
1
2
3
4
5
6

Количество баллов
3
2
5
6
3
6

Всего баллов
25 баллов


1. a) Запишите в виде .

b) Найдите .

  1. Зная, что k – натуральное число, выполните эскиз графика функции

y = xr , где
r = −n, n = 1,5k.

  1. Дана функция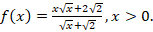

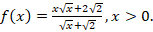
a) Покажите, что

b) Найдите

c) Вычислите




  1. Решите систему уравнений: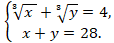




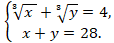
  1. Решите неравенство: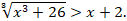




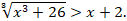
  1. Упростите выражение: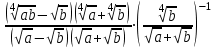
  1. 1   ...   11   12   13   14   15   16   17   18   ...   59

Схема выставления баллов





№
Ответ
Балл
Дополнительная информация

1а


1





1 b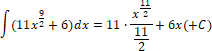









1

Принимается ответ без +С






или эквивалент
1



2



y =





1






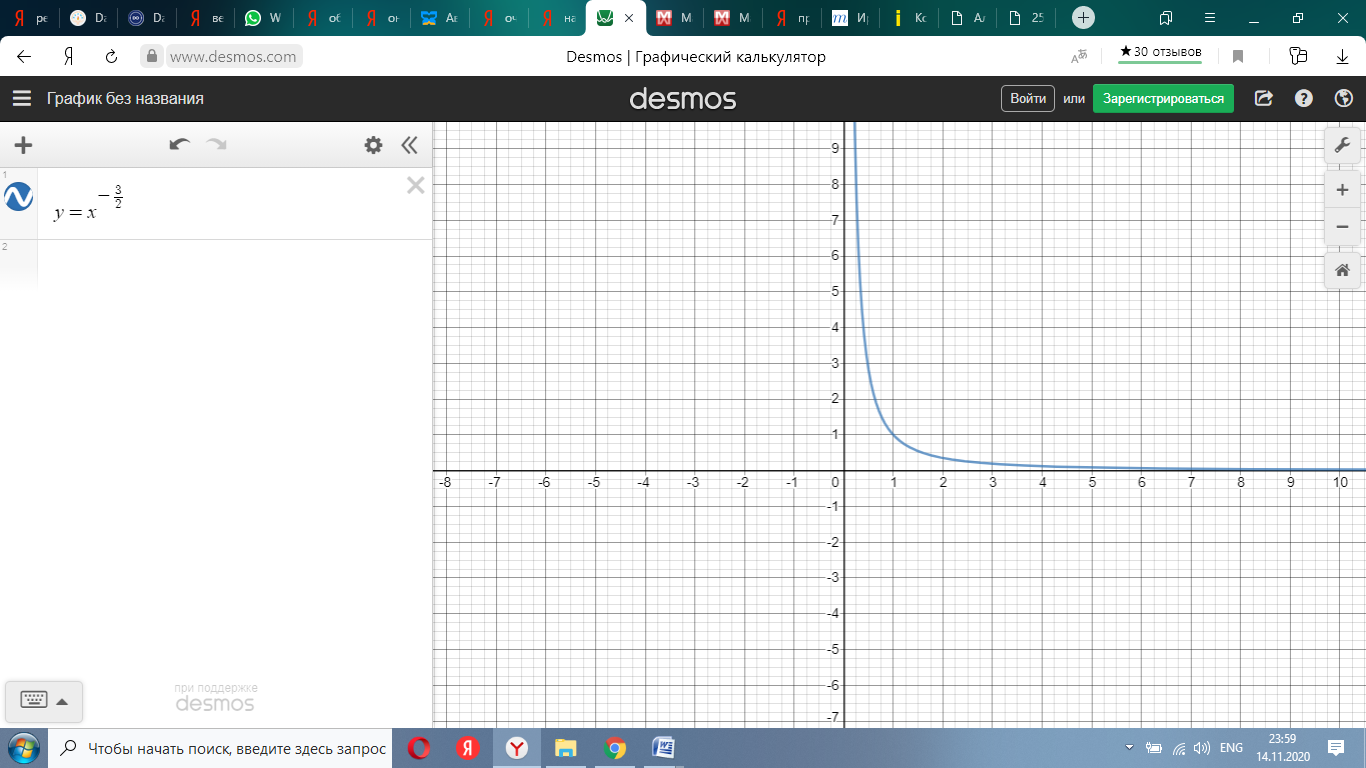1




3 a



1
За использование формулы суммы кубов

или эквивалент
1




3 b


1
Допускаются ошибки в знаках

или эквивалент
1



3 c
0,5
1



4


1



)


1





1



.
1
За решение квадратного

уравнения

,

.
1



(1;27), (27,1)
1




5


1





1





1



6


1
Применяется альтернативная запись



1





1





1





1



1
1



Итого
25




2 ВАРИАНТ

Оценивание заданий работы

№ задания
1
2
3
4
5
6

Количество баллов
3
2
5
6
3
6

Всего баллов
25 баллов

1. a) Запишите в виде .

b) Найдите .

  1. Зная, что k – натуральное число, выполните эскиз графика функции

y = xr , где r =

Смотрите также файлы