Файл: Сборник работ для суммативного оценивания по алгебре и началам анализа 11 класс.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 4588
Скачиваний: 247
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «СТЕПЕНИ И КОРНИ. СТЕПЕННАЯ ФУНКЦИЯ»
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»
1. Прямоугольный треугольник с гипотенузой 10 см и проведенной к ней высотой равной 4,8 см вращается вокруг гипотенузы.
a) Выполните рисунок по условию задачи.
b) Найдите площадь поверхности тела, полученного при вращении.
2. Высота конуса 4, радиус его основания 5. Выполните рисунок по условию задачи и найдите площадь сечения, проведенного через вершину, если расстояние от него до центра основания конуса равно 2,4.
3. Диагонали ромба 3 см и 4 см. Шаровая поверхность касается всех его сторон. Радиус шара 2 см.
a) Выполните рисунок по условию задачи.
b) Найдите расстояние от центра шара до плоскости ромба.
4. Радиус оснований усеченного конуса 12 м и 24 м, высота 16 м.
a) Выполните рисунок по условию задачи.
b) Найти образующую.
5.Высота цилиндра 6 дм, радиус основания 5 дм. Концы отрезка АВ, равного 10 дм, лежат на окружностях обоих оснований. Выполните рисунок к задаче и найдите кратчайшее расстояние от него до оси.
Схема выставления баллов
| № | Ответ | Балл | Дополнительная информация |
| 1 a |  | 1 | Выполнен рисунок по условию задачи |
| 1 b | Показано, что высота прямоугольного треугольника является радиусом двух конусов. | 1 | |
| Показан метод нахождения полной поверхности первого и второго конуса. | 1 | | |
| 168π см2 | 1 | | |
| 2 |  | 1 | Выполнен рисунок по условию задачи |
| Определяется данное расстояние от центра основания до плоскости | 1 | Используются формулы синуса, косинуса, тангенса острого угла в прямоугольном треугольнике | |
| Находится площадь сечения | 1 | ||
| 100 | 1 | | |
| 3 |   | 1 | Выполнены рисунки по условию задачи |
| Используется теорема о трех перпендикулярах | 1 | | |
| Используется площадь ромба | 1 | ||
| 3,2 см | 1 | | |
| 4 |  | 1 | Выполнен рисунок по условию задачи |
| Определяется метод нахождения диаметров верхнего и нижнего поверхностей усеченного конуса | 1 | | |
| Показано осевое сечение усеченного конуса | 1 | | |
| 20 м | | ||
| 5 | 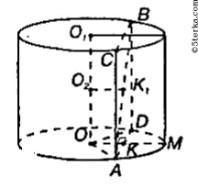 | 1 | Выполнен рисунок по условию задачи |
| Выясняется фигура сечения в цилиндре | 1 | | |
| Определяется метод нахождения расстояния от отрезка АВ до оси цилиндре | 1 | | |
| Используется радиус и высота цилиндра | 1 | | |
| 3 дм | 1 | | |
| Итого: | 20 | | |
ВАРИАНТ 4
| Разбаловка заданий работы | |||||
| № задания | 1 | 2 | 3 | 4 | 5 |
| Количество баллов | 4 | 4 | 4 | 3 | 5 |
| итого | 20 баллов | ||||
1 ... 49 50 51 52 53 54 55 56 ... 59
1. Прямоугольный треугольник с гипотенузой 25 см и проведенной к ней высотой равной 12 см вращается вокруг гипотенузы.
a) Выполните рисунок по условию задачи.
b) Найдите площадь поверхности тела, полученного при вращении.
2. Высота конуса 12, радиус его основания 15. Выполните рисунок по условию задачи и найдите площадь сечения, проведенного через вершину, если расстояние от него до центра основания конуса равно 7,2.
3. Диагонали ромба 9 см и 12см. Шаровая поверхность касается всех его сторон. Радиус шара 6 см.
a) Выполните рисунок по условию задачи.
b) Найдите расстояние от центра шара до плоскости ромба.
4. Радиус оснований усеченного конуса 1,5 м и 3м, высота 2 м.
a) Выполните рисунок по условию задачи.
b) Найдите образующую.
5. Высота цилиндра 2 м. Радиус основания 7 м. В этот цилиндр наклонно вписан квадрат — так, что все вершины его лежат на окружностях оснований. Выполните рисунок к задаче и найдите сторону квадрата.
Схема выставления баллов
| № | Ответ | Балл | Дополнительная информация |
| 1 a |  | 1 | Выполнен рисунок по условию задачи |
| 1 b | Показано, что высота прямоугольного треугольника является радиусом двух конусов. | 1 | |
| Показан метод нахождения полной поверхности первого и второго конуса. | 1 | | |
| 420π см2 | 1 | | |
| 2 |  | 1 | Выполнен рисунок по условию задачи |
| Определяется данное расстояние от центра основания до плоскости | 1 | Используются формулы синуса, косинуса, тангенса острого угла в прямоугольном треугольнике | |
| Находится площадь сечения | 1 | ||
| 300 | 1 | | |
| 3 |   | 1 | Выполнены рисунки по условию задачи |
| Используется теорема о трех перпендикулярах | 1 | | |
| Используется площадь ромба | 1 | ||
| 12,8 см | 1 | | |
| 4 |  | 1 | Выполнен рисунок по условию задачи |
| Определяется метод нахождения диаметров верхнего и нижнего поверхностей усеченного конуса | 1 | | |
| Показано осевое сечение усеченного конуса | 1 | | |
| 2,5 м | | ||
| 5 | 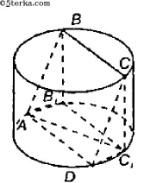 | 1 | Выполнен рисунок по условию задачи |
| Проводятся дополнительные отрезки, пепендикулярные плоскости основания | 1 | | |
| Определяется метод нахождения стороны квадрата, вписанного в цилиндр наклонно | 1 | | |
| Используется радиус и высота цилиндра | 1 | | |
| 10 м | 1 | | |
| Итого: | 20 | | |
1 ... 51 52 53 54 55 56 57 58 59
-
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ
Продолжительность - 40 минут
Количество баллов – 20
Типы заданий:
МВО – задания с множественным выбором ответов;
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 5 заданий, включающих вопросы с кратким и развернутым ответами.
В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов.
Задание может содержать несколько структурных частей/вопросов
Характеристика заданий суммативного оценивания
| Раздел | Проверяемая цель | Уровень мыслительных навыков | Кол. заданий* | № задания* | Тип задания* | Время на выполнение, мин* | Балл* | Балл за раздел |
| Объемы тел | 11.3.18 - решать задачи практического содержания на комбинации геометрических тел | Применение | 2 | 1 a,b,c | КО/РО | 10 | 5 | 20 |
| 3 | РО | 10 | 5 | |||||
| 11.3.15 - знать формулы нахождения объемов конуса и усеченного конуса и применять их при решении задач | Применение | 1 | 1 c | РО | 4 | 2 | ||
| 11.3.13 - знать формулы нахождения объема пирамиды и усеченной пирамиды и применять их при решении задач | Применение | 1 | 2 | РО | 8 | 4 | ||
| 11.3.12 - знать формулу нахождения объема призмы и применять ее при решении задач | Применение | 1 | 4 | РО | 8 | 4 | ||
| ИТОГО: | | | 5 | | | 40 | 20 | 20 |
| Примечание: * - разделы, в которые можно вносить изменения | ||||||||
ЗАДАНИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ
| Разбаловка заданий работы | ||||
| № задания | 1 | 2 | 3 | 4 |
| Количество баллов | 7 | 4 | 5 | 4 |
| итого | 20 баллов | |||
1 ... 51 52 53 54 55 56 57 58 59