Файл: Решение одноиндексных оптимизационных задач Цель работы научиться решать одноиндексные оптимизационные задачи производства.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 149
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рис. 2.20. Окно «Добавление ограничений»
Добавляем ограничения для неравенств:
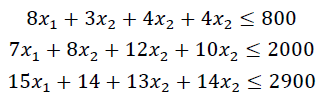
В поле «Ссылка на ячейки» указываем адрес диапазона F9:F11, выбираем в раскрывающемся списке знак неравенства ≤, в поле Ограничение выделяем диапазон G9:G11 и нажимаем кнопку «Добавить». Результатом этого действия будет добавление текущего ограничения в список ограничений, поля окна Добавление ограничения будут очищены для ввода следующего ограничения.
Порядок ввода ограничений не имеет значения. Главное — не забыть ни одно из ограничений.
Покажем окна для добавления остальных ограничений.
х1≤12≤30 (рис. 2.21, 2.22).
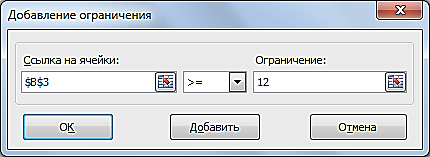
Рис. 2.21. Добавление левой части ограничения по х1
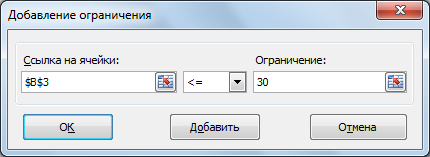
Рис. 2.22. Добавление правой части ограничения по х1
х2≤25 - (рис. 2.23).
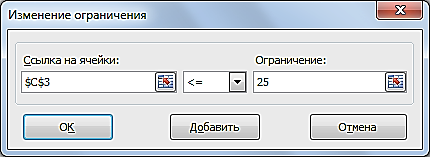
Рис. 2.23. Добавление ограничения по х2
х3≥25 - (рис. 2.24).
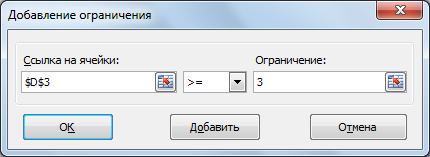
Рис. 2.24. Добавление ограничения по х3
Ограничения х2≥0 и х4≥0 можно не добавлять, т.к. в окне «Параметры поиска решения» установлен флажок в поле «Сделать переменные без ограничений неотрицательными».
Для принятия последнего ограничения и возврата к диалоговому окну «Параметры поиска решения» нажмем кнопку OK.
После указания всех необходимых параметров в диалоговое окно Параметры поиска решения примет вид (рис. 2.25):
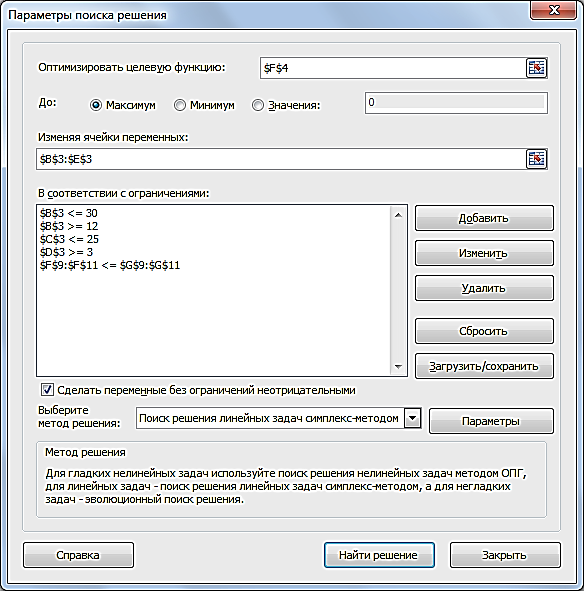
Рис. 2.25. Окно «Параметры поиска решения» с ограничениями
После нажатия кнопки «Найти решение» отобразится окно «Результаты поиска решения» (рис. 2.26).
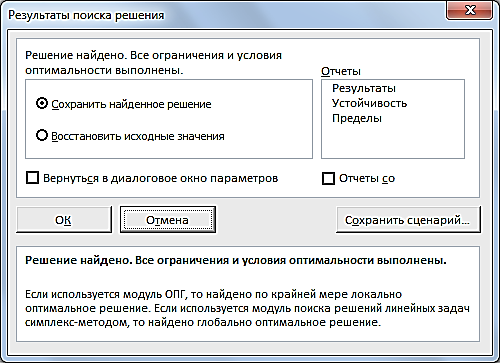
Рис. 2.26. Окно «Результаты поиска решения»
Для сохранения полученного решения необходимо установить переключатель «Сохранить найденное решение» и нажать кнопку ОК. После
чего на рабочем листе отобразится решение задачи (рис. 2.27).
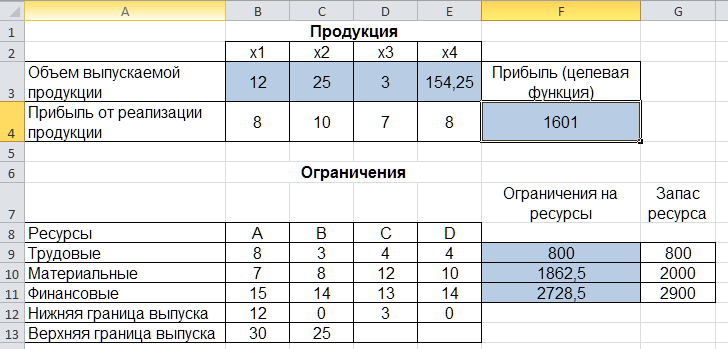
Рис. 2.27. Результаты решения задачи
Таким образом, максимальная прибыль при реализации продукции будет получена в размере 1601 д. е. при следующем плане производства:
Кроме вставки оптимальных значений в изменяемые ячейки, «Поиск решения» позволяет представлять результаты в виде трех отчетов: «Результаты, Устойчивость и Пределы». Для генерации одного или нескольких отчетов необходимо выделить их названия в окне диалога «Результаты поиска решения» (рис. 2.26). Для выбора нескольких отчетов из списка использовать клавишу Shift.
Рассмотрим более подробно каждый из них.
Отчет по результатам (рис. 2.28) содержит три таблицы: в первой приведены сведения о целевой функции до начала вычисления и окончательное значение, во второй – значения искомых переменных: исходные и полученные в результате решения задачи, в третьей – результаты оптимального решения для ограничений.
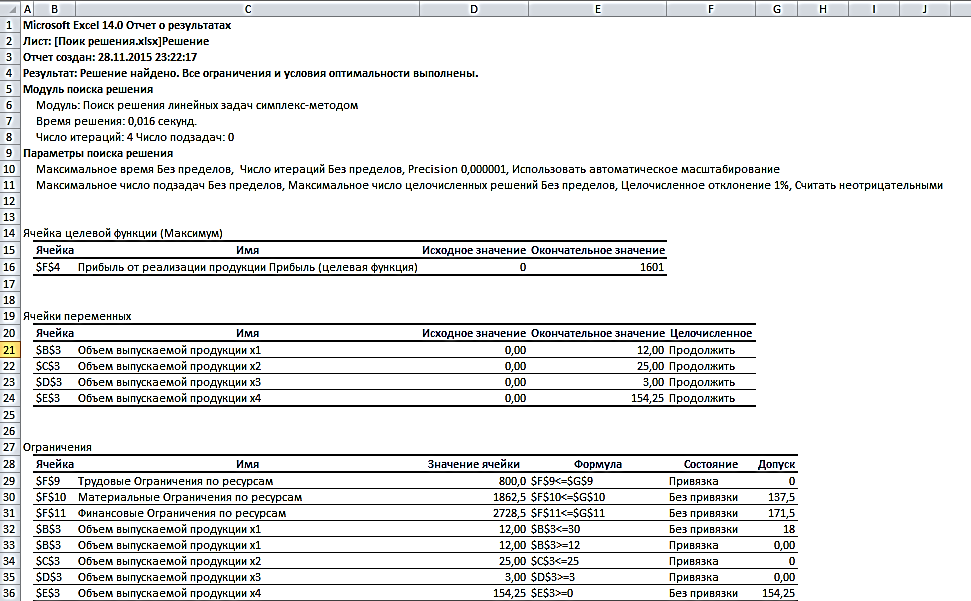
Рис. 2.28. Отчет о результатах
Этот отчет также содержит информацию о таких параметрах каждого ограничения, как состояние и допуск. Состояние принимает значение «Привязка», если вводимые ограничения совпадают с ограничениями, полученными в результате вычислений, и значение «Без привязки» в противном случае.
По значениям столбца «Допуск» можно сделать вывод о недоиспользованных ресурсах. В рассматриваемой задаче трудовые ресурсы были использованы полностью (значение в столбце «Допуск» равно 0), материальные ресурсы использованы не полностью (недоиспользованными оказались 137,5 единиц), также недоиспользовано 171,5 ед. финансовых
ресурсов.
Отчет по устойчивости (рис. 2.29) содержит два блока: Ячейки переменных и Ограничения. Первый блок содержит информацию по допустимому увеличению и уменьшению коэффициентов целевой функции при условии, что объем оптимальной продукции не изменится. Второй блок касается увеличения и уменьшения значений ограничений.
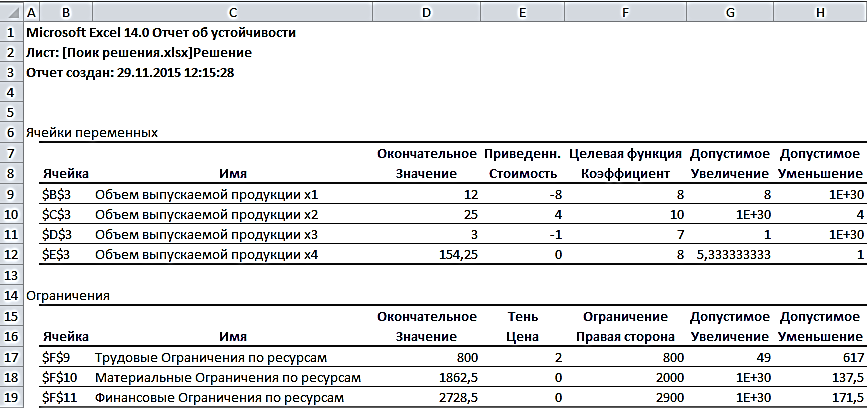
Рис. 2.29. Отчет по устойчивости
Отчет по пределам (рис. 2.30) содержит информацию о том, в каких пределах значения изменяемых ячеек могут быть увеличены или уменьшены без нарушения ограничений задачи. Для каждой изменяемой ячейки этот отчет содержит оптимальное значение, а также наименьшие значения, которые ячейка может принимать без нарушения ограничений.
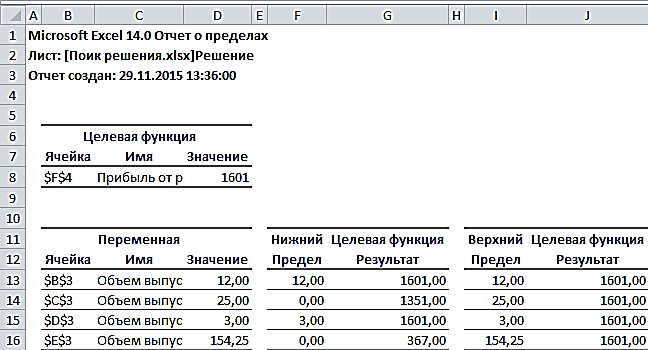
Рис. 2.30. Отчет о пределах
При сохранении книги Excel после выполнения поиска решения все значения, введенные в окнах диалога «Поиск решения», сохраняются вместе с данными рабочего листа. С каждым рабочим листом в рабочей книге можно сохранить один набор значений параметров «Поиска решения».
Кнопка «Сохранить сценарий» окна «Результаты поиска решения» (рис. 2.31) позволяет сохранить сценарий текущей модели. Все сценарии доступны в «Диспетчере сценариев», который открывается командой «Данные - Работа с данными - Анализ что-если - Диспетчер сценариев».
Задача проверки сбалансированности плана
Рассмотрим решение предыдущей задачи при измененных условиях. Предположим при сложившейся ситуации на рынке продукцию вида D сняли с производства и взамен планируется выпуск продукции вида Е. Поменялись предельно допустимые значения выпуска некоторых видов. Все исходные данные по расходу, запасам ресурсов, предельно допустимым значениям выпуска каждого вида даны в табл. 2.7.
Таблица 2.7. Условие задачи 2
Прибыль от реализации единицы продукции равны: 8 д. е. – для A, 10 д. е. – для B, 7 д. е. – для C, 12 д. е. – для Е.
Необходимо определить объем продукции каждого вида, чтобы прибыль от реализации продукции была максимальной.
Решение. Составим математическую модель для решения поставленной задачи.
Обозначим переменные:
Прибыль от реализации продукции
составит:
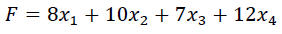
Ограничения для переменных:
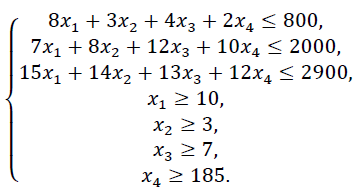
Математическая постановка данной задачи состоит в нахождении такого неотрицательного решения системы линейных уравнений, при котором целевая функция F принимает максимальное значение.
Создадим на рабочем листе таблицу для ввода исходных данных. Введем в созданную таблицу исходные данные, целевую функцию, ограничения и граничные условия (рис. 2.31).
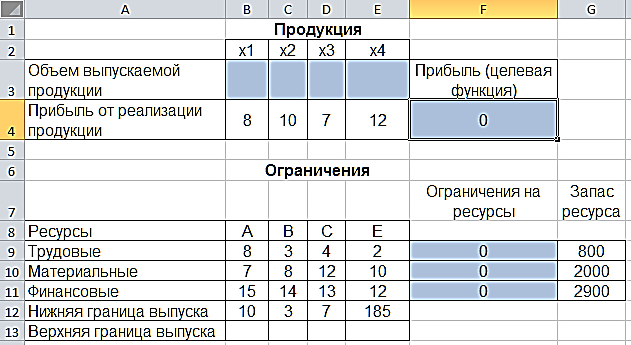
Рис. 2.31. Исходные данные для задачи 2
В формульном варианте таблица будет иметь вид (рис. 2.32):
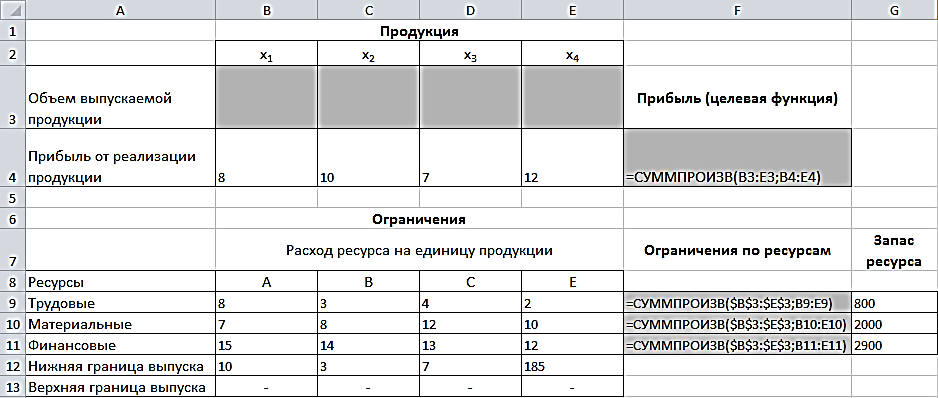
Рис. 2.32. Формулы для вычислений
На вкладке «Данные» в группе «Анализ» выберем команду «Поиск решения». На экране отобразится диалоговое окно «Параметры поиска решения», в котором установим необходимые параметры (рис. 2.33):
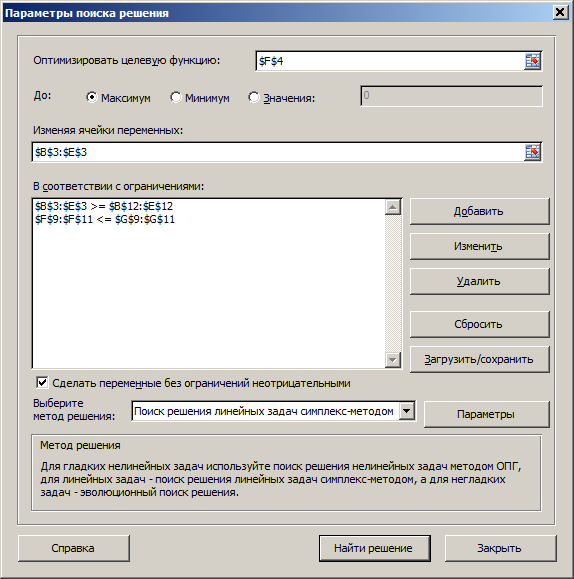
Рис. 2.33. Окно «Параметры поиска решения» задачи 2
После выбора кнопки Найти решение отобразится окно Результаты поиска решения (рис. 2.34).
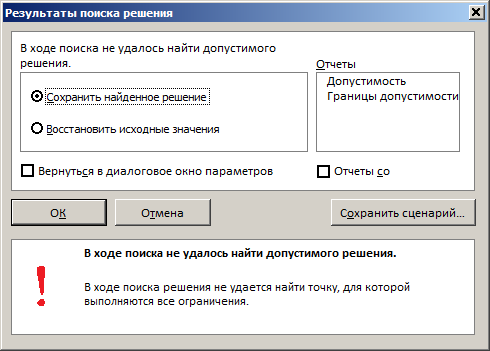
Рис. 2.34. Окно «Результаты поиска решения» задачи 2
В данном окне дано сообщение, что в результате решения данной задачи не удалось найти допустимого решения. Выведем отчет о допустимости (рис 2.35).
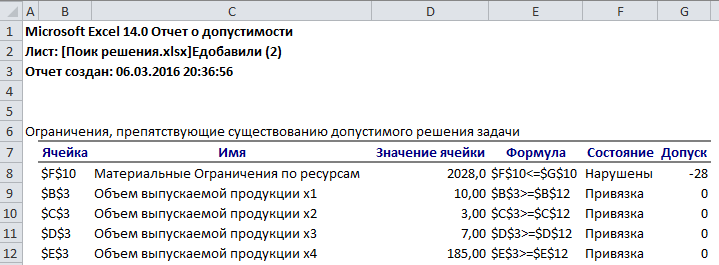
Рис. 2.35. Отчет о допустимости
По отчету о допустимости делаем вывод, что задача не сбалансирована по материальным ресурсам. Действительно, если подставим нижние границы выпуска продукции во второе уравнение системы , то материальных ресурсов для выполнения плана не хватит:
7*10+8*3+12*7+10*185 = 2028
Добавляем ограничения для неравенств:
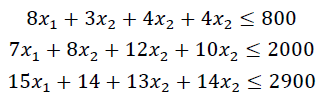
В поле «Ссылка на ячейки» указываем адрес диапазона F9:F11, выбираем в раскрывающемся списке знак неравенства ≤, в поле Ограничение выделяем диапазон G9:G11 и нажимаем кнопку «Добавить». Результатом этого действия будет добавление текущего ограничения в список ограничений, поля окна Добавление ограничения будут очищены для ввода следующего ограничения.
Порядок ввода ограничений не имеет значения. Главное — не забыть ни одно из ограничений.
Покажем окна для добавления остальных ограничений.
х1≤12≤30 (рис. 2.21, 2.22).

Рис. 2.21. Добавление левой части ограничения по х1

Рис. 2.22. Добавление правой части ограничения по х1
х2≤25 - (рис. 2.23).

Рис. 2.23. Добавление ограничения по х2
х3≥25 - (рис. 2.24).

Рис. 2.24. Добавление ограничения по х3
Ограничения х2≥0 и х4≥0 можно не добавлять, т.к. в окне «Параметры поиска решения» установлен флажок в поле «Сделать переменные без ограничений неотрицательными».
Для принятия последнего ограничения и возврата к диалоговому окну «Параметры поиска решения» нажмем кнопку OK.
После указания всех необходимых параметров в диалоговое окно Параметры поиска решения примет вид (рис. 2.25):

Рис. 2.25. Окно «Параметры поиска решения» с ограничениями
После нажатия кнопки «Найти решение» отобразится окно «Результаты поиска решения» (рис. 2.26).

Рис. 2.26. Окно «Результаты поиска решения»
Для сохранения полученного решения необходимо установить переключатель «Сохранить найденное решение» и нажать кнопку ОК. После
чего на рабочем листе отобразится решение задачи (рис. 2.27).

Рис. 2.27. Результаты решения задачи
Таким образом, максимальная прибыль при реализации продукции будет получена в размере 1601 д. е. при следующем плане производства:
-
12,00 – объем продукции типа А; -
25,00 – объем продукции типа B; -
3,00 – объем продукции типа C; -
154,25– объем продукции типа D.
Кроме вставки оптимальных значений в изменяемые ячейки, «Поиск решения» позволяет представлять результаты в виде трех отчетов: «Результаты, Устойчивость и Пределы». Для генерации одного или нескольких отчетов необходимо выделить их названия в окне диалога «Результаты поиска решения» (рис. 2.26). Для выбора нескольких отчетов из списка использовать клавишу Shift.
Рассмотрим более подробно каждый из них.
Отчет по результатам (рис. 2.28) содержит три таблицы: в первой приведены сведения о целевой функции до начала вычисления и окончательное значение, во второй – значения искомых переменных: исходные и полученные в результате решения задачи, в третьей – результаты оптимального решения для ограничений.

Рис. 2.28. Отчет о результатах
Этот отчет также содержит информацию о таких параметрах каждого ограничения, как состояние и допуск. Состояние принимает значение «Привязка», если вводимые ограничения совпадают с ограничениями, полученными в результате вычислений, и значение «Без привязки» в противном случае.
По значениям столбца «Допуск» можно сделать вывод о недоиспользованных ресурсах. В рассматриваемой задаче трудовые ресурсы были использованы полностью (значение в столбце «Допуск» равно 0), материальные ресурсы использованы не полностью (недоиспользованными оказались 137,5 единиц), также недоиспользовано 171,5 ед. финансовых
ресурсов.
Отчет по устойчивости (рис. 2.29) содержит два блока: Ячейки переменных и Ограничения. Первый блок содержит информацию по допустимому увеличению и уменьшению коэффициентов целевой функции при условии, что объем оптимальной продукции не изменится. Второй блок касается увеличения и уменьшения значений ограничений.

Рис. 2.29. Отчет по устойчивости
Отчет по пределам (рис. 2.30) содержит информацию о том, в каких пределах значения изменяемых ячеек могут быть увеличены или уменьшены без нарушения ограничений задачи. Для каждой изменяемой ячейки этот отчет содержит оптимальное значение, а также наименьшие значения, которые ячейка может принимать без нарушения ограничений.

Рис. 2.30. Отчет о пределах
При сохранении книги Excel после выполнения поиска решения все значения, введенные в окнах диалога «Поиск решения», сохраняются вместе с данными рабочего листа. С каждым рабочим листом в рабочей книге можно сохранить один набор значений параметров «Поиска решения».
Кнопка «Сохранить сценарий» окна «Результаты поиска решения» (рис. 2.31) позволяет сохранить сценарий текущей модели. Все сценарии доступны в «Диспетчере сценариев», который открывается командой «Данные - Работа с данными - Анализ что-если - Диспетчер сценариев».
Задача проверки сбалансированности плана
Рассмотрим решение предыдущей задачи при измененных условиях. Предположим при сложившейся ситуации на рынке продукцию вида D сняли с производства и взамен планируется выпуск продукции вида Е. Поменялись предельно допустимые значения выпуска некоторых видов. Все исходные данные по расходу, запасам ресурсов, предельно допустимым значениям выпуска каждого вида даны в табл. 2.7.
Таблица 2.7. Условие задачи 2
| Ресурсы | Расход ресурса на единицу продукции | Запас ресурса | |||
| A | B | C | Е | ||
| Трудовые | 8 | 3 | 4 | 2 | 800 |
| Материальные | 7 | 8 | 12 | 10 | 2000 |
| Финансовые | 15 | 14 | 13 | 12 | 2900 |
| Нижняя граница выпуска | 10 | 3 | 7 | 185 | |
| Верхняя граница выпуска | – | – | – | – | |
Прибыль от реализации единицы продукции равны: 8 д. е. – для A, 10 д. е. – для B, 7 д. е. – для C, 12 д. е. – для Е.
Необходимо определить объем продукции каждого вида, чтобы прибыль от реализации продукции была максимальной.
Решение. Составим математическую модель для решения поставленной задачи.
Обозначим переменные:
-
x1 – объем произведенной продукции вида А; -
x2 – объем произведенной продукции вида B; -
x3 – объем произведенной продукции вида C; -
x4 – объем произведенной продукции вида Е.
Прибыль от реализации продукции
составит:
Ограничения для переменных:
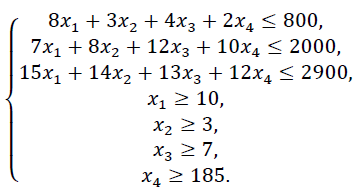
Математическая постановка данной задачи состоит в нахождении такого неотрицательного решения системы линейных уравнений, при котором целевая функция F принимает максимальное значение.
Создадим на рабочем листе таблицу для ввода исходных данных. Введем в созданную таблицу исходные данные, целевую функцию, ограничения и граничные условия (рис. 2.31).

Рис. 2.31. Исходные данные для задачи 2
В формульном варианте таблица будет иметь вид (рис. 2.32):

Рис. 2.32. Формулы для вычислений
На вкладке «Данные» в группе «Анализ» выберем команду «Поиск решения». На экране отобразится диалоговое окно «Параметры поиска решения», в котором установим необходимые параметры (рис. 2.33):

Рис. 2.33. Окно «Параметры поиска решения» задачи 2
После выбора кнопки Найти решение отобразится окно Результаты поиска решения (рис. 2.34).

Рис. 2.34. Окно «Результаты поиска решения» задачи 2
В данном окне дано сообщение, что в результате решения данной задачи не удалось найти допустимого решения. Выведем отчет о допустимости (рис 2.35).

Рис. 2.35. Отчет о допустимости
По отчету о допустимости делаем вывод, что задача не сбалансирована по материальным ресурсам. Действительно, если подставим нижние границы выпуска продукции во второе уравнение системы , то материальных ресурсов для выполнения плана не хватит:
7*10+8*3+12*7+10*185 = 2028