Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx

Скачать файл (2,25Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 30.11.2023

Просмотров: 139

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

b

h

n

2
    

   ^h      

I_T_f

a

xdx



i1

^fi1 ^fi

₂f₀

2 f₁

2 f₂

...

²^fn1

f_n. (3.6)

Для удобства вычислений формулу (3.6) записывают следующим обра-

зом:

b
  ^

f₀ f_n

n1 _

I_T _f

^x^dx^^h

2

^_^fi ^.

_a i1 

Вид представленной формулы позволяет сделать вывод, что она может быть сформирована также исходя из других соображений, так как получае- мый с ее применением результат является средним арифметическим резуль- татов использования формул левых (3.3) и правых (3.4) прямоугольников.

Поэтому

_I_I_L I_RT ₂

и указанное утверждение справедливо для случаев

равных и неравных шагов интегрирования.

Замечание. Несмотря на то, что в методе трапеций для аппроксимации подынтегральной функции используются полиномы первой степени, по сравнению с методами прямоугольников, которые используют полиномы ну- левой степени, точность метода трапеций оказывается ниже точности метода средних прямоугольников. Более высокая точность метода средних прямо- угольников объясняется «удачным» выбором узловых точек для вычисления значений подынтегральной функции.

Метод Симпсона (метод парабол)

Аппроксимацию функции

fx

по методу трапеций можно

интерпретировать как замену исходной функции

fx

некоторой кусочно-

линейной функцией. Ошибка метода в данном случае определяется

«грубостью» предложенного способа аппроксимации функции. Естественно

допустить, что если исходную функцию

fx

аппроксимировать на

частичных отрезках не линейными функциями, а полиномами более высоких порядков, то ошибка соответствующего метода численного интегрирования должна уменьшиться. В методе Симпсона в качестве функции, с помощью

которой на частичных отрезках интегрирования заменяется исходная

функция

fx^,^{выбрана}^{парабола.}

Пояснение. Более высокая точность вычисления интегралов обеспечивается при использовании параболической аппроксимации (полиномом второй

степени)

y ax²  bx c

по трем соседним точкам. Для нахождения

^{коэффициентов}^a^,b^и^c^{полинома,}^{проходящего}^через^точкиx₀, y₀^,

x₁, y₁^,x₂, y₂^,^{требуется}^найти^{решение}^{следующей}^{системы}^{линейных}уравнений

^y₀ ax²  bx

_0 0

1
_y₁ ax²  bx₁ c,

^y₂ ax²  bx c,

_2 2

относительно неизвестных a, b, c.

Разделим отрезок интегрирования a,b

на четное число nравных от-

^рез^к^ов^с^ш^а^га^м^иh^.^Н^а^ка^ж^дом^о^т^рез^к^еx_i_₁, x_i_₁

длиной

2h, содержащем

три узла x_i_₁, x_i, x_i_₁, заменим подынтегральную функцию полиномом вто- рой степени _ix  ax²  bx c. Пример представлен на рис. 5.

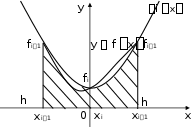
Рис. 5. Пример замены функции

y fx ^{параболой.}

Для рассматриваемого примера значения коэффициентов a, bи cмо- гут быть вычислены следующим образом:

^ah²  bh c

^fi1 ^,


^c f,

i


^ah²  bh c

^fi1 ^,

^откудаc

f_i^,

2ah²  2 f_i

^fi1 ^

f_i_₁, a

f_i_₁ 2 f_i

2h²

^fⁱ^¹, а b

^fi1 ^

2h

^fi1 _.

В результате рассматриваемый полином второй степени примет вид

fx  _i

x 

f_i

^fi1 ^

2h

^fi1 _x_

f_i_₁ 2 f_i

2h²

^fi1 _x²_.

^И^нтег^ри^р^у^я^п^р^и^в^е^д^е^н^н^ое^в^ы^р^а^же^н^ие^на^от^р^езкеx_i_₁, x_i_₁^,^по^л^у^ч^и^м

^xi1

^xi1 _

f  f

f  2 f f ₂ _h

__ixdx _

__f_i_i1 i1 _x_i1 i i1 _x

_dx

 f_i_₁ 4 f_i f_i_₁.

(3.7)

^xi1

^xi1 ^²^h

2h² _³

Приближенное значение интеграла на исходном отрезке интегрирова-

ния a,b

получим суммированием частичных интегралов (3.7) по всем от-

^резкамx_i_₁, x_i_₁^:

b
  

__hn21__

  

I _f

a

xdx



³i0

^f2i

⁴^f2i1

^f2i2

(3.8)

 ^h f

₃0

 4 f₁

 2 f₂

 4 f₃

 2 f₄

 ...  2 f
n2

n1 ^

f_n.

Полученное соотношение называется формулой Симпсона или

формулой парабол, в соответствии с которой искомый определенный

Смотрите также файлы

Конкурса Семейная память.docx

Урок Формирование единых государств в Европе и России.docx

Логическое моделирование основано На основе десятичных логарифмов.docx

Анализ ассортимента детского питания в аптеке.docx

Самые большие современные птицы.docx

Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx

b
  ^

Метод Симпсона (метод парабол)

Смотрите также файлы

Информация

Списки файлов

Дополнительно

Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx

b  

Метод Симпсона (метод парабол)

Смотрите также файлы

Информация

Списки файлов

Дополнительно

b
  ^