Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 137
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, образованного вращением фигуры, ограни- ченной графиками функций (аналитически и с помощью программы wxMax- ima). В вариантах 1–20 ось вращения Ox , в вариантах 21–40 ось вращения Oy.





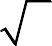
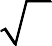








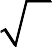
Если дуга гладкой кривой
y f(x) ,
a x b, вращается вокруг оси
Ox, то площадь поверхности вращения вычисляется по формуле
b
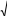 Sx 2 y
Sx 2 y
a
1 y2 dx
Пример. Найти площадь поверхности, образованной вращением вокруг оси
Oxплоской фигуры ограниченной линиями
y x3,
x 0,
x 2 .
Найдем производную
y 3x2 , тогда
2 2
2 2 1
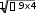 S 2 x3
S 2 x3
dx 2 x3
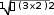
dx
19x4 2d1 9x4

x
36
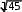 0 0 0
0 0 0
2
 2 1 9x4 32
2 1 9x4 32
14532 1
145
1
18 3
0 27 27
Для решения подобных задач в Maxima следует выполнить следую- щиедействия:
Пример 11. Найти площадь поверхности, образованной вращением вокруг
оси Oxдуги кривой ???? = sin 2???? от ???? = 0 до ???? = .
2
Введем функции:
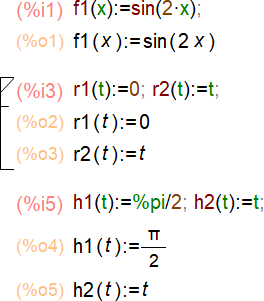
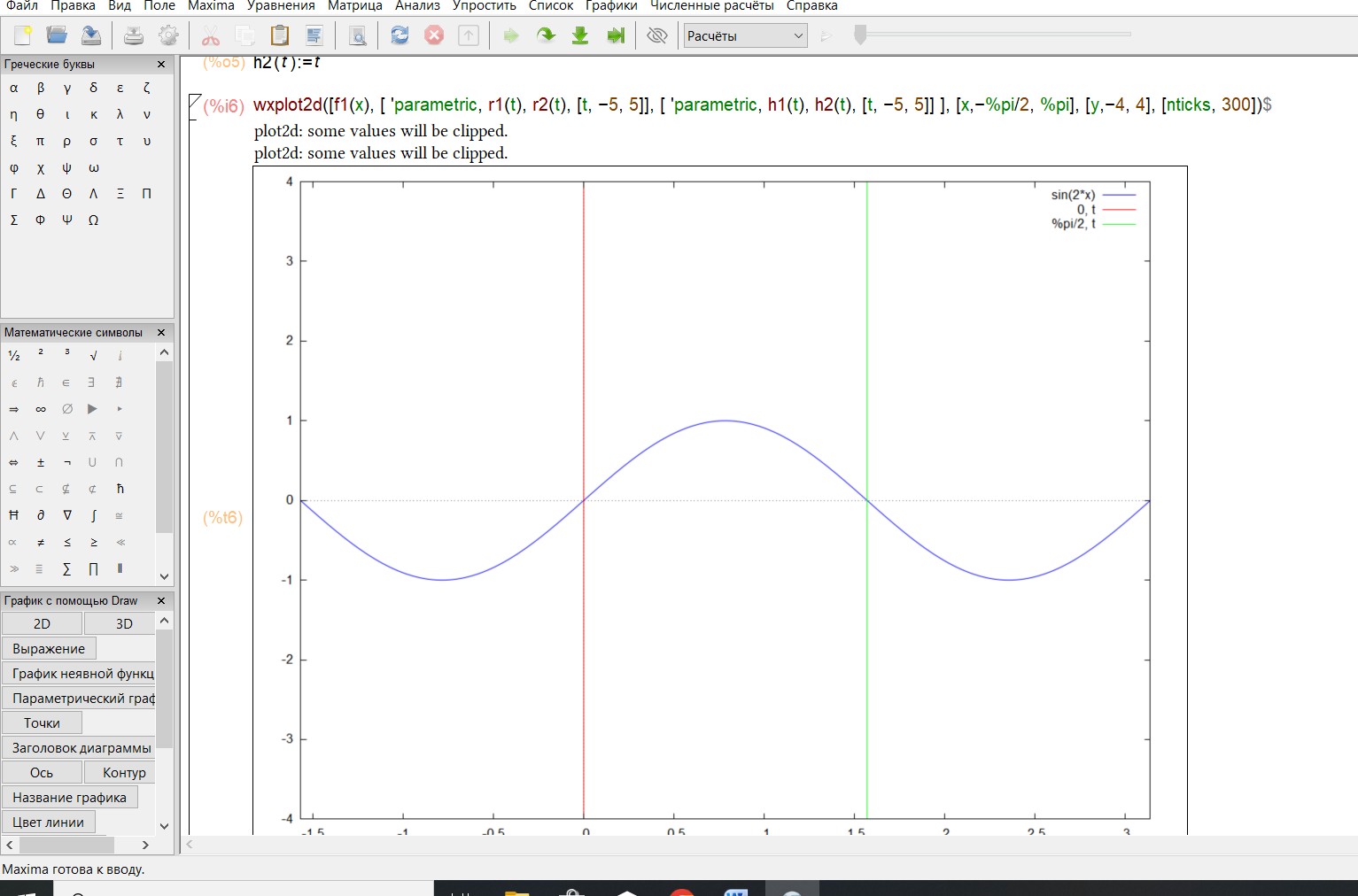
Построим график функций:
Найдем производную и вычислим интеграл
ex e x
Гиперболический косинус:
ch x .
2
ex e x
Гиперболический синус:
sh x .
2
Гиперболический тангенс:
th x
sh x
ch x
ex e x
ex e x
ch x
ex e x
Гиперболический котангенс:
cth x sh x ex e x .
 Гиперболический ареасинус: Arsh x ln x x2 1
Гиперболический ареасинус: Arsh x ln x x2 1
Гиперболический ареакосинус:
Arch x lnx
x2 1 lnx
x2 1
 Гиперболический ареатангенс:
Гиперболический ареатангенс:
Arth x 1 ln 1 x
2 1 x
Гиперболический ареакотангенс:
Arcth x 1 ln x 1
| 1 | y x2 5x 6, y 0. |
| 2 | 2x x2 y 0, 2x2 4x y 0. |
| 3 | y 3sin x, y sin x, 0 x . |
| 4 | y 5cos x, y cos x, x 0, x 0. |
| 5 | y sin2 x, x 2, y 0. |
| 6 | x 3 y 2, x 1, y 1. |
| 7 | y xex, y 0, x 1. |
| 8 | y 2x x2, y x 2, x 0. |
| 9 | y 2x x2, y x 2. |
| 10 | y e1x, y 0, x 0, x 1. |
| 11 | y x2 , y2 x 0. |
| 12 | x2 y 22 1. |
| 13 | y 1 x2, x 0, x y 2, x 1. |
| 14 | y x2, y 1, x 2. |
| 15 | y x3, y x. |
| 16 | y sin x2, y x2. |
| 17 | x2 y , y 12 2x, x 0. 4 |
| 18 | y xex, y 0, x 1. |
| 19 | x2 x3 y , y . 2 8 |
| 20 | y xex, y 0, x 1. |
| 21 | y x1, y 0, y 1, x 0,5. |
| 22 | y ln x, x 2, y 0. |
| 23 | y x12 , y 1. |
| 24 | y2 x 2, y 0, y x3, y 1. |
| 25 | y x3, y x2. |
| 26 | y arccos x5, y arccos x3, y 0. |
| 27 | y arcsin x, y arccos x, y 0. |
| 28 | y x2 2x1, x 2, y 0. |
| 29 | y x3, y x. |
| 30 | y arccos x, y arcsin x, x 0. |







| 31 | y x12 , x 0, x 2, y 0. |
| 32 | y arccos x3, y arccos x, y 0. |
| 33 | y x2, x 2, y 0. |
| 34 | y x2 1, y x, x 0, y 0. |
| 35 | y arcsin x5, y arcsin x, y 2. |
| 36 | y x12 , y 1. |
| 37 | x2 x3 y , y . 2 8 |
| 38 | y x12 , x 1, x 2, y 0. |
| 39 | y 3 x, x=8, y 0. |
| 40 | x2 y , y 12 2x, y 0. 4 |






- 1 2 3 4 5 6 7 8 9 10 ... 15
Площадь поверхности вращения
Если дуга гладкой кривой
y f(x) ,
a x b, вращается вокруг оси
Ox, то площадь поверхности вращения вычисляется по формуле
b
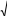 Sx 2 y
Sx 2 ya
1 y2 dx
Пример. Найти площадь поверхности, образованной вращением вокруг оси
Oxплоской фигуры ограниченной линиями
y x3,
x 0,
x 2 .
Найдем производную
y 3x2 , тогда
2 2
2 2 1
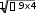 S 2 x3
S 2 x3dx 2 x3
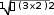
dx
19x4 2d1 9x4

x
36
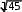 0 0 0
0 0 0
2
 2 1 9x4 32
2 1 9x4 32 14532 1
145
1
18 3
0 27 27
Для решения подобных задач в Maxima следует выполнить следую- щиедействия:
-
Построить кривую. -
Вычислить производные функции. -
В зависимости от способа задания кривой, составить и вычис- литьопределенный интеграл с помощью программы Maxima и вручную. -
Записать ответ.
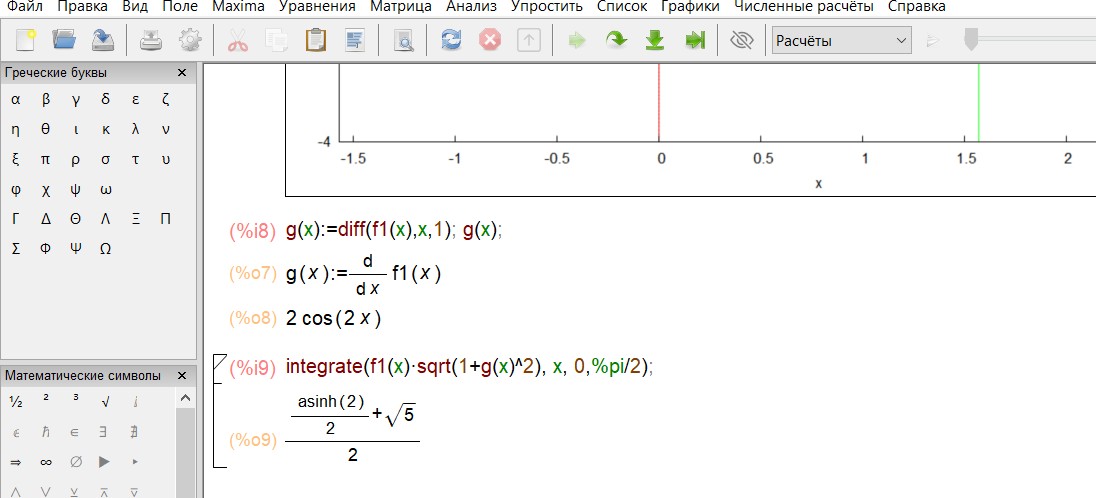
Пример 11. Найти площадь поверхности, образованной вращением вокруг
оси Oxдуги кривой ???? = sin 2???? от ???? = 0 до ???? = .
2
Введем функции:
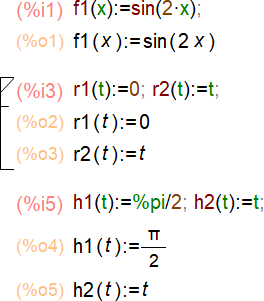
Построим график функций:

Найдем производную и вычислим интеграл

Справочная информация:
ex e x
Гиперболический косинус:
ch x .
2
ex e x
Гиперболический синус:
sh x .
2
Гиперболический тангенс:
th x
sh x
ch x
ex e x
ex e x
ch x
ex e x
Гиперболический котангенс:
cth x sh x ex e x .

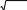
 Гиперболический ареасинус: Arsh x ln x x2 1
Гиперболический ареасинус: Arsh x ln x x2 1Гиперболический ареакосинус:
Arch x lnx
x2 1 lnx
x2 1
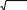
 Гиперболический ареатангенс:
Гиперболический ареатангенс:Arth x 1 ln 1 x
2 1 x
Гиперболический ареакотангенс:
Arcth x 1 ln x 1