ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 327
Скачиваний: 11
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
Обзор суммативного оценивания
Продолжительность - 40 минут
Количество баллов – 20
Типы заданий:
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 6 заданий, включающие вопросы с краткими и развернутыми ответами.
В заданиях, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В заданиях, требующие развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/ вопросов.
Характеристика заданий суммативного оценивания
| Раздел | Проверяемая цель | Уровень мыслительных навыков | Кол. заданий* | № задания* | Тип задания* | Время на выполнение, мин* | Балл* | Балл за раздел |
| Векторы на плоскости | 9.1.4.5 знать определение угла между двумя векторами | Знание и понимание | 1 | 1 | КО | 2 | 2 | 20 |
| 9.1.4.4 раскладывать вектор по двум неколлинеарным векторам | Применение | 1 | 2 | РО | 5 | 2 | ||
| 9.1.4.2 знать и применять правила сложения векторов и умножения вектора на число | Применение | 1 | 3 | РО | 2 | 3 | ||
| 9.1.3.3 выполнять действия над векторами в координатах | Применение | 1 | 4 | РО | 6 | 3 | ||
| 9.1.3.4 знать и применять скалярное произведение векторов и его свойства | Применение | 1 | 5 | РО | 10 | 5 | ||
| 9.1.4.7 решать задачи векторным методом | Навыки высокого порядка | 1 | 6 | РО | 15 | 5 | ||
| ИТОГО: | | | 6 | | | 40 | 20 | 20 |
| Примечание: * - разделы, в которые можно вносить изменения | ||||||||
ЗАДАНИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ
| Оценивание заданий работы | ||||||
| № задания | 1 | 2 | 3 | 4 | 5 | 6 |
| Количество баллов | 2 | 2 | 3 | 3 | 5 | 5 |
| Всего баллов | 20 баллов | |||||
1 ВАРИАНТ
-
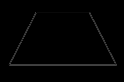
Четырехугольник ABCD – трапеция,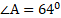
. Найдите угол между векторами
и .
-
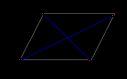
Диагонали параллелограмма PMCK пересекаются в точке О. Выразите вектор КО
через векторы и .
-
Упростите выражение
-
Найдите длину вектора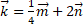
, где 
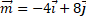и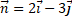 
. -
Даны вектор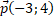
, 
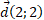и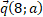 
. Найдите:
а) косинус между векторами и ;
b) число а, если векторы и коллинеарны;
с) число а, если векторы и перпендикулярны.
6. Решите задачу векторным методом. Выполните рисунок.
Дан треугольник с вершинами М (-2;8), N (6;2), K(2;-6). Найдите длину медианы МР.
Схема выставления баллов
| № | Ответ | Балл | Дополнительная информация | ||
| 1 |  | 1 | | ||
 | 1 | | |||
| 2 |  | 1 | | ||
 | 1 | | |||
| 3 |  | 1 | | ||
 | 1 | | |||
 | 1 | | |||
| 4 |  | 1 | | ||
 | 1 | | |||
 | 1 | | |||
| 5 | | 1 | | ||
 | 1 | | |||
 или  | 1 | | |||
| b)  | 1 | | |||
| | 1 | | |||
| 6 | Верно выполнен рисунок к задаче | 1 | | ||
| М(х;у)  | 1 | | |||
| М (4;-2). Верно построена медиана МР | 1 | | |||
 | 1 | | |||
 | 1 | | |||
| Итого: | 20 | | |||
2 ВАРИАНТ
| Оценивание заданий работы | ||||||
| № задания | 1 | 2 | 3 | 4 | 5 | 6 |
| Количество баллов | 2 | 2 | 3 | 3 | 5 | 5 |
| Всего баллов | 20 баллов | |||||
1 2 3 4 5 6 7 8 9 ... 13
-
Четырехугольник ABCD – ромб,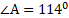
. Найдите угол между векторами
и .
-
Диагонали параллелограмма PMCK пересекаются в точке О. Выразите вектор РО
через векторы и .
-
Упростите выражение
-
Найдите длину вектора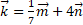
, где 
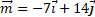и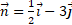 
. -
Даны вектор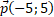
, 
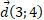и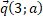 
. Найдите:
а) косинус между векторами и ;
b) число а, если векторы и коллинеарны;
с) число а, если векторы и перпендикулярны.
6. Решите задачу. Дан параллелограмм с вершинами М (3;-4), N (-5;3), K(1;2), L (х; у). Найдите сумму координат вершины L.
Схема выставления баллов
| № | Ответ | Балл | Дополнительная информация | ||
| 1 |  | 1 | | ||
 | 1 | | |||
| 2 |  | 1 | | ||
 | 1 | | |||
| 3 |  | 1 | | ||
 | 1 | | |||
| | 1 | | |||
| 4 |  | 1 | | ||
 | 1 | | |||
 | 1 | | |||
| 5 | а)  | 1 | | ||
 | 1 | | |||
 или  | 1 | | |||
| b)  | 1 | | |||
| | 1 | | |||
| 6 |  , | 1 | | ||
 | 1 | | |||
| х-3=6, х= 9 | 1 | | |||
| у+4=-1, у=-5 | 1 | | |||
| L (9; -5), 9-5=4 | 1 | | |||
| Итого: | 20 | | |||
