Файл: азастан республикасыны білім жне ылым министрлігі ОРыт ата атындаЫ ызылорда мемлекеттік университеті жаратылыстану институты.docx

x_i айнымалыларының n мәндері беріледі, олардың негізде f(x₁,…x_n) функциясының мәні есептеледі және де бұл мән m шығыс байланыстарына жіберіледі. Екі жақтылықты желісінде бұл элемент шығысында _i екі жақтылықты сигналдарының m терімін алады да, олардың қосындысын  есептейді де әрбір n кірістеріне  мен сигналдың сәйкес кірісіне берілетін мәні бойынша жеке туынды функциясының f(x₁,…x_n) туындысының көбейтіндісін береді. Бұл процесс 1-суретте көрсетілген. Онда екі жақтылықты желі құрылғанда барлық тараулану нүктелері оларға екі жақтылықты элементтеріне – қарапайым сумматорларға көшетіні көрінеді.

Сурет 1- Нейрожелісінің абстрактілі элементінің тура және екі жақтылықты функционалуы

Енді формалді нейронға екі жақтылықты нейронды құру процесін қарастырамыз. Ол үшін формалді нейронды (4 сурет) толығырақ қарастырайық (2 сурет), онда нейронның кіріс адаптивті сумматорын жұптық (синапс салмағы мен синапсқа келуші сигналдың) көбейтіндісін есептейтін элементтердің терімі мен қарапайым сумматор түрінде қарайық. Формалді нейронды құрастыратын барлық элементтерін жоғарыда баяндалған екі жақтылықты элемент құру ережеге сәйкес қайта құрамыз. Формалді нейронға екі жақтылықты нейрон және оның жұмыс істеу ережелері 3-ші суретте көрсетілген. Осында екі жақтылықты желіні құрғанда барлық қарапайым сумматорлар оларға екі жақтылықты элементтеріне – тараулану нүктелеріне өтетіні көрінеді. Осы фактіні көбірек көркемдеу үшін 2-ші суретте адаптивті сумматорды қарапайым сумматоры мен синапстардың терімі түрінде ұсынуы қолданылған болатын. Екі жақтылықты желісі формалді нейрондарға екі жақтылықты нейрондарынан құрылады. Әрине, екі жақтылықты желілер нейрондардың контрукциясы күрделірек болатын желілер үшін де құрылуы мүмкін.

Сонымен, берілген желісіне екі жақтылықты желі құрылды. Енді қазір соңғы қабаттың нейрондарының шығысына берілетін екі жақтылықты айнымалыларын  анықтаймыз. Екі жақтылықты желі көмегімен берілген желісінің ішкі құрылған параметрлері бойынша бағалау функциясының градиентін есептеу есебін шешу үшін, екі жақтылықты айнымалылары ретінде желінің шығыс сигналдары бойынша бағалау функциясының жеке туындыларын H алу қажетті. Онда желінің барлық элементтері мен кіріс сигналдары үшін бұл параметрлердің мен сигналдардың мәндері бойынша бағалау функцияларының жеке туындылары есептеп шығарылған болады.

---

С
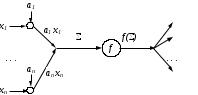
урет 2 - Формальді нейронның функционалуы

С
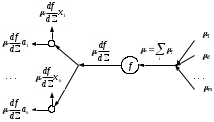
урет 3 - Формальді нейронның екі жақтылықты функционалуы



Сурет 4- Формальді нейрон

Градиент есептеуіне екі жақтылықты желіні қолдану градиенттің бүкіл векторын есептеу уақыты берілген желісінің әдеттегі жұмыс істеуі кезіндегі шығыс сигналдарын есептеу уақытысынан не бары 2-3 есе үлкен болады. Бұның себебі, барлық орындалатын әрекеттердің ұйымшыл болуы, есептеулердің қайталаусыз іске асырылған, және де градиент барынша көп параллельді тәртіпте есептеледі.

Градиенттің есептеуіне екі жақтылықты жұмыс істеуін қолдану үшін нейрондық желілер мен бағалау функциясына қойылатын жалғыз талабы ол бағалау функциялары мен желісінің барлық элементтерінің олардың кіріс сигналдары бойынша үзіліссіз бірінші туындыларының бар болуы.
Лекцияда пайдаланылатын слайдтар:

1. 
   Желінің жолдық параметрлері бойынша бағалау функциясының градиенті.
   

Пайдаланылған әдебиеттер тізімі:

Негізгі әдебиет

1. 
   Галушкин, А.И. Применения нейрокомпьютеров в финансовой деятельности [Текст] / А.И. Галушкин. – Новосибирск: Наука, 2002. – 215с.
   
2. 
   Ефимов, Д.В. Нейросетевые системы управления [Текст] / Д.В. Ефимов. – М.: Высшая школа, 2002. — 184 с.
   

Қосымша әдебиеттер

1. 
   Уоссермен, Ф. Нейрокомпьютерная техника: Теория и практика [Текст] / Ф. Уоссермен. — М.: Мир, 2006. — 240 с.
   

Бақылау сұрақтары:

1. 
   Желінің ішкі құрылған параметрлері бойынша бағалау функциясының градиенті қалай есептеледі?
   
2. 
   Градиент есептеуіне екі жақтылықты желіні қолдану градиенттің бүкіл векторын есептеу уақыты берілген желісінің әдеттегі жұмыс істеуі кезіндегі шығыс сигналдарын есептеу уақытысынан айырмашылығы қандай?
   

Лекция 14. Желі сигналдары мен көрсеткіштерін есептеу параметрлері

1. 
   Желі сигналдары мен көрсеткіштерін есептеу параметрлері.
   

Лекция мақсаты:

---

Желі сигналдары мен көрсеткіштерін есептеу параметрлерін толығымен таныстыру.

Қарастырылатын негізгі сөздер: Нерондық желі, координата, n-өлшемді векторлар, параметрлер, синапстар және т.б.

Нейрондық желісінде координаталары xji, j=1,..,n болатын xi, i=1,..,N (есептер жинағы) мәліметтердің n-өлшемді векторлардың терімі, координаталары ak, k=1,..,M болатын бар a параметрлерінің M-өлшемді векторы және x мәліметтер векторының a параметрлерімен желінің жұмысын бағалайтын қандай да бір H(x,a) бағалау функциясы бар. Желісінің ең аз мәнді ak параметрлерін мен xj сигналдарын бөліп алып, бұл параметрлер мен мәліметтердің компоненттерін алып тастап, желіні түрлендіру қажет [1-3].

Әрбір a_k үшін қандай да бір a_k⁰ мәні анықталған және a_k қысқарту a_k=a_k⁰ деген теңестіруді білдіреді. Дәл осылай мәліметтердің әрбір x_j компонентасы мен кез келген xⁱ үлгісі үшін x_jⁱ⁰ анықталған және i–ші үлгісі үшін мәліметтердің j-ші компонентасын алып тастау x_j = x_jⁱ⁰ деген теңестіруді білдіреді.

Осындай процедура баяндауды қысқарту процедурасының қайта анықтауда өте үлкен бостандықты береді. Ең қарапайым негізгі вариант ретінде әрбір i үшін a_k⁰=0 деп қарастырамыз.



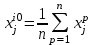
Параметрлер нольге айналып, мәліметтер сұрыптаудың орташа мәнімен ауыстырылады. Мысалы, [-1,1] диапазонына нормаланған мәліметтер жағдайында x_jⁱ⁰ ретінде, әрине, ноль алынады.

Маңыздылық көрсеткіштері екі кезеңімен анықталады: ең алдымен олар мәліметтердің (үлгінің) бір векторы үшін, ал одан кейін – бүкіл сұрыптауы бойынша есептеледі.

x^p мәліметі үшін a_k мен x_j маңыздылықтары осылайша бағаланады:

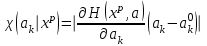, (1.3)

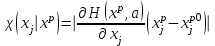, (1.4)

мұндағы  - баяндауды қысқартқандағы H өзгерісінің сызықты жуықтауда есептелген абсолютті шамалары.

Бүкіл есептер жинағы бойынша бағалау қандай да бір норманы пайдаланып, мысалы, модульдерінің қосындысы түріндегі норманы пайдаланып есептелінеді:

---

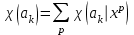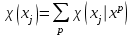; , (1.5)

немесе модульдерінің максимумы.

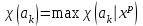
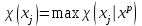, (1.6).

Мысалы, оқыту кезінде, өзінің параметрлерін өзгертетін жүйені өте жиі кездестіруге болады. Сонда маңыздылық туралы шешім қабылау сәтіне әр түрлі нүктелердегі a=a¹,..,a^q Hдербес туындылар туралы ақпарат жиналуы мүмкін. Онда бір мәліметтердің векторы үшін маңыздылық көрсеткіштері осылай есептеледі:

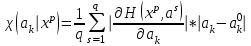, (1.7)

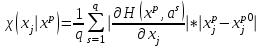, (1.8).

Туындылардың абсолютті мәндері орташаландырылады, ал өсімше қысқарту процедурасы іске асырылатын нүктесінде алынады. Одан әрі бүкіл сұрыптауы бойынша маңыздылық көрсеткіштері белгілі бір норма бойынша орташаландырылады.

Осындай тәсілмен есептелген маңыздылық көрстекіштерін пайдалану желінің кіріс сигналдарының (есепті дұрыс шешуге қажетті қасиеттердің минималды терімі ғана қалады) және элементтерінің санын өте қатты қысқартуға мүмкіндік береді.

Егер желіден адаптивті элементтерді алып тастамай, олардың мәндерін белгіленген мәндердің ақырғы теріміне келтіру қажет болса, онда әрбір a_k үшін a_k⁰ ретінде a_k ең жақын белгіленген мәні алынады. Осындай есеп, мысалы, желінің синапстарының салмақтарын бинаризациясы кезінде – синапстарының салмақтарын –1 немесе 1 деген шамаларға келтіру - пайда болады.
Лекцияда пайдаланылатын слайдтар:

1. 
   Желі сигналдары мен көрсеткіштерін есептеу параметрлері.
   

Пайдаланылған әдебиеттер тізімі:

Негізгі әдебиет

1. 
   Галушкин, А.И. Применения нейрокомпьютеров в финансовой деятельности [Текст] / А.И. Галушкин. – Новосибирск: Наука, 2002. – 215с.
   
2. 
   Ефимов, Д.В. Нейросетевые системы управления [Текст] / Д.В. Ефимов. – М.: Высшая школа, 2002. — 184 с.
   

Қосымша әдебиеттер

1. 
   Уоссермен, Ф. Нейрокомпьютерная техника: Теория и практика [Текст] / Ф. Уоссермен. — М.: Мир, 2006. — 240 с.
   

Бақылау сұрақтары:

1. 
   Ең қарапайым негізгі вариант ретінде әрбір i үшін a_k⁰=0 деп x-тің өрнегін жазыңыз
   
2. 
   Баяндауды қысқартқандағы H өзгерісінің сызықты жуықтауда есептелген абсолютті шамасының белгіленуі
   
3. 
   Синапстардың салмақтарны қандай шамаға келтіру тиімді болып есептеелінеді?
   

---

Лекция 31-32. Нейрондық желілер теориясының элементтері. Семантикалық нейрондық желілер

1. 
   Нейрокибернетиканың дамуы.
   
2. 
   Мак–Каллок–Питтс нейронының формалды моделі.
   
3. 
   Нейрондық желінің жұмыс кезеңдері.
   
4. 
   Семантикалық нейрондық желілер. 
   

Лекция мақсаты: Нейрокибернетиканың дамуының маңыздылығын, формалды модельдің қолданысын және желінің жұмыс жасау кезеңдерін студенттерге жан-жақты түсіндіру.

Қарастырылатын негізгі сөздер: Нейрокибернетика, нейрофизиолог, нейрондық желілер, нейронтәрізді элементтер, алгоритм, ассоциативті жады, формалды модель, сигнал, қабаттар, семантикалық нейрондық желілер және т.б.

Нейрокибернетиканың дамуына үлкен қарқын берген американдық нейрофизиолог Френк Розенблатт болып табылады. Ол 1962 жылы нейрондық желінің өз моделі – персептронды ұсынды. Алғашында үлкен энтузиазммен қабылданған ол кейін ірі ғылыми беделді кісілердің интенсивті шабуылына ұшырады.

1982 жылы американдық биофизик Дж. Хопфилд нейрондық желінің дербес моделін ұсынды, ол өз атымен аталды. Келесі жылдары көптеген тиімді алгоритмдер табылды: қарама-қарсы ағын желісі, екі жақты ассоциативті жады, т.б.

Нейрондық желілерде білімдер нейротәрізді элементтердің (немесе жай ғана нейрондар) жиынының күйінде және олардың арасындағы байланыстарда сақталады.

Мак–Каллок–Питтс нейронының қазіргі кезде де жеке нейронды сипаттау үшін қолданылып жүрген формалды моделі төменде көрсетілген.



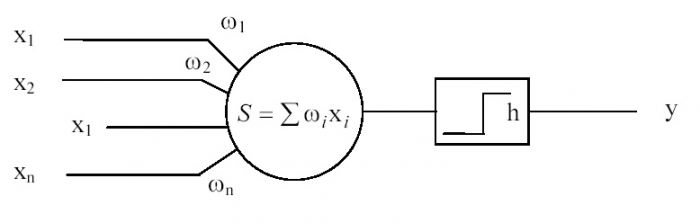
Мак–Каллок – Питтс нейронының формалды моделі

Мұндағы xi – нейронның i кірісіндегі (синапс) сигнал;

wi – нейронның i кірісіндегі (синапс) салмақ;

y – нейронның шығысы;

h – нейронның жұмыс жасау табалдырығы.

Моделде нейронның кірісіндегі сигналдар сомасы h табалдырықты мәнімен салыстырылып, егер ол сол мәннен артық болса, шығыста сигнал қалыптасады. Нейрондардың қазіргі моделдерінде табалдырықты функция жалпы жағдайда беру функциясы немесе нейронды белсенді ету функциясы деп аталатын сызықты емес y="f"(S) функциясымен алмастырылады.

Белгілі бір түрде байланысқан нейрондардан қандай да бір кірістер және шығыстар саны бар нейрондық желі құрылады. Әдетте түйіндердің (нейрондардың) үш типін ажыратады – кіріс (нейрондардың кіріс қабаты немесе Input layer), шығыс (шығыс қабат немесе Output layer) және жасырын қабаттар (Hidden layers) (төмендегі суретті қараңыз).

---