Файл: Курс лекций по дисциплине Эконометрика.doc

Пример АКФ и частной АКФ для модели MА(2) представлен на рис. 5.9; 5.10. Для модели MА(q) все значения АКФ для лагов, больших q, равны нулю. Для модели ARMA(р, q) значения АКФ после лага p-q представляют собой смесь затухающих синусоид и экспонент, а значения частной АКФ ведут себя аналогично после лага q-p. 

Рис. 5.9	Рис. 5.10

Общий подход Бокса-Дженкинса к анализу временных рядов показан на рис. 5.11. Схема процесса выбора модели временного ряда показана на рис. 5.12.

Если процесс выбора модели успешно осуществлен, возникает проблема оценки качества построенной модели. Для «хорошей» модели остатки должны быть «белым шумом», т.е. их выборочные автокорреляции не должны значимо отклоняться от нуля. Кроме того, модель не должна содержать лишних параметров, т.е. нельзя уменьшить число параметров без появления значимой автокорреляции остатков. Для диагностики модели необходимо попытаться модифицировать ее, меняя порядки авторегрессии и скользящего среднего. Одновременно повышать оба порядка не рекомендуется ввиду опасности вырождения модели.

5.7. Тестирование стационарности временного ряда

Как было отмечено выше, стационарные временные ряды имеют следующие отличительные черты: значения ряда колеблются вокруг постоянного среднего значения с постоянной дисперсией, которая не зависит от времени, АКФ затухает с увеличением лага. При анализе экономических явлений чаще приходится иметь дело с нестационарными временными рядами, которые не имеют постоянного среднего, дисперсия которых зависит от времени, а АКФ затухает очень медленно. Для подбора модели ряда и прогнозирования его значений необходимо уметь распознавать тип временного ряда.

Рассмотрим процесс авторегрессии первого порядка

y(t)=y(t-1)+(t).

Ряд y(t) является стационарным рядом, если –1<<1. Если =1, то y(t) – нестационарный временной ряд – случайное блуждание со сдвигом: в этом случае считают, что временной ряд

---

y(t) имеет единичный корень.

Вычтем y(t-1) из обеих частей модели: y(t)=y(t-1)+(t), где =-1.

Дики и Фуллер рассмотрели три регрессии:

y(t)=y(t-1)+(t),

y(t)=₀+y(t-1)+(t),

y(t)=₀+y(t-1)+₂t+(t).

Вторая регрессия содержит постоянный элемент ₀, а третья, кроме этого, и линейный временной тренд. Во всех трех регрессиях интересующий параметр .

Нулевая гипотеза H₀: =0 против альтернативы H₁: <0.

Тест Дики-Фуллера (Dickey-Fuller) состоит в следующем. Оцениваются методом наименьших квадратов одно из указанных выше уравнений.




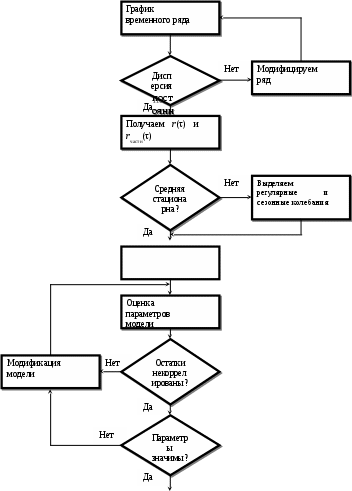
Прогнозирование

Рис. 5.11. Подход Бокса-Дженкинса


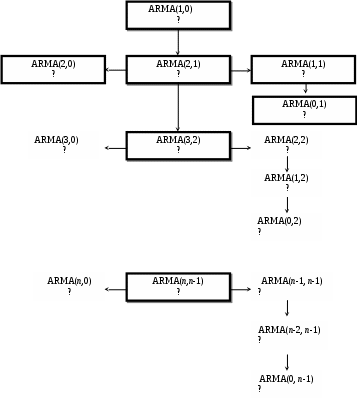
Рис. 5.12. Процесс выбора ARIMA модели

Получают оценку , стандартную ошибку и соответствующее значение t – статистики. Сравнивая значение t-статистики с табличным, определяют, принять или отклонить H₀. Критическое значение t-статистики имеет нестандартное распределение и зависит от формы регрессии и объема выборки – см в [5].

Критические значения не изменятся, если указанные выше модели заменить авторегрессионным процессом произвольного порядка:

y(t)=y(t-1)+ +(t),

y(t)=₀+y(t-1)+ +(t),

y(t)=₀+y(t-1)+₂t+ +(t).

Для последних моделей Дики и Фуллер предложили три дополнительные статистики для тестирования обобщенных гипотез о коэффициентах:

₁: H₀: =₀=0.

₂: H₀: =₀=₂=0.

₃: H₀: =₂=0.

Статистики _i конструируются как F тест: , i=1,2,3, где RSS_r и RSS_ur – квадраты ошибок короткой и длинной регрессий, g – число исключенных переменных, n – число наблюдений

---

, k – число параметров в длинной регрессии. Большие значения _i ведут к отклонению нулевой гипотезы. Критические значения статистик вычислены Дики и Фуллером и затабулированы.
5.8. Эконометрический анализ взаимосвязанных временных рядов

Коинтеграция и мнимая регрессия.

Рассмотрим два временных ряда y_t и x_t. Предположим, что оба ряда имеют единичные корни, то есть являются нестационарными. Предположим далее, что исследователь не знает механизмов, порождающих y_t и x_t, и оценивает регрессию:

y_t =x_t + _t, t=1,…,n. (5.12)

Если _t = y_t – x_t, t=1,…,n является стационарным временным рядом, то временные ряды y_t и x_t называются коинтегрированными, а вектор (1 –) называется коинтегрирующим вектором.

Примеры.

1. Длинная ставка процента R, короткая ставка процента r: _t=R_t – r_t, вектор коинтеграции (1 –1).

2. Логарифм потребления C_t, логарифм дохода y_t: _t=С_t – y_t, вектор коинтеграции (1 –1).

3. Логарифм обменного курса D_t, логарифм внутренней цены P_t, логарифм цен мирового рынка P_t^*: _t=D_t –P_t+P_t^*, вектор коинтеграции (1 –1 1). 

В случае коинтегрируемости временных рядов говорят о долгосрочном динамическом равновесии. Если y_t и x_t коинтегрированы, то y_t и x_t содержат общую нестационарную компоненту – долговременную тенденцию, а разность y_t – x_t стационарна и совершает флуктуации около нуля.

Таким образом, коинтеграция временных рядов – причинно-следственная зависимость в уровнях временных рядов, которая выражается в совпадении или противоположной направленности их тенденций и случайной колеблемости.

Возможен случай, когда ошибка _t = y_t – x_t, t=1,…,n в регрессии (5.12) является нестационарным временным рядом. Тогда условия классической регрессионной модели (п. 3) не выполняются, в частности дисперсия _t не является постоянной. Кроме того, МНК оценка параметра  не состоятельна, поэтому с ростом объема выборки увеличиваются шансы получения ложных выводов о взаимосвязи

---

y_t и x_t. Такая ситуация называется ложной (мнимой) регрессией. На практике признаками мнимой регрессии являются высокое значение R² и малое значение статистики Дарбина-Уотсона.

Для проверки рядов на коинтеграцию используются тесты Энгеля-Гранжера или Йохансена.

Пример. Рассмотрим временные ряды логарифмов доходов и расходов на потребление с августа 1990 г. по январь 1992 г. в России. Графический анализ – рис. 5.1 показывает, что тенденции этих рядов совпадают.

Расчет параметров уравнения регрессии логарифма расходов y_t на логарифм доходов x_t обычным МНК дает следующие результаты:

=0,9x_t + _t,

n=25, R²=0,80, критерий Дарбина-Уотсона 1,85, стандартная ошибка коэффициента регрессии 0,009.

Для тестирования рядов на коинтеграцию определим оценки остатков = - 0,9x_t и построим регрессию первых разностей  на :

 = - 0,95 .

Фактическое значение t-критерия для коэффициента последней регрессии равно –4,46, что превышает по абсолютной величине критическое значение 1,94, рассчитанное Энгелем и Гранжером, при уровне значимости 5%, т.е. с вероятностью 0,95 можно утверждать, что временные ряды логарифмов доходов и расходов на потребление коинтегрированы. 

При изучении двух взаимосвязанных временных рядов на предварительной стадии регрессионного анализа рекомендуется устранить сезонные или циклические колебания, если они имеются в исследуемых временных рядах, в соответствии с принятой аддитивной или мультипликативной моделями рядов.

Если рассматриваемые временные ряды y_t и x_t содержат тенденцию, то коэффициент корреляции, характеризующий степень зависимости между y

---

_t и x_t будет иметь высокое значение. Такая же ситуация будет иметь место тогда, когда y_t и x_t зависят от переменной времени t. Как в первом, так и во втором случае имеет место ложная корреляция, которая приводит при построении регрессии y_t на x_t вида (5.12) к автокорреляции в остатках и нестационарности ряда остатков регрессии (ложная регрессия), то есть к нарушению предпосылок МНК.



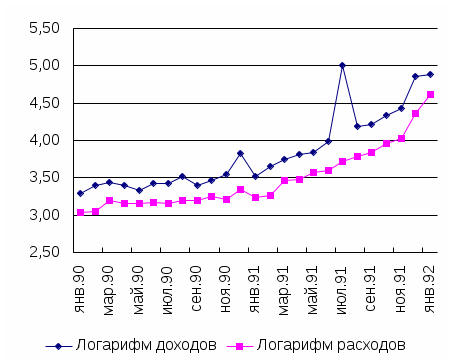
Рис. 5.13.
Для получения регрессии со стационарным временным рядом остатков _t, как уже указывалось ранее, может быть использован метод последовательных разностей, когда переход к некоторым k-м разностям уровней ряда позволяет получить стационарный ряд остатков.

Другими методами исключения тренда из анализируемой модели (5.12) являются методы включения фактора времени и отклонений от тренда.

Метод включения фактора времени.

Для устранения влияния времени на результат и факторы при изучении взаимосвязанных рядов динамики используется прием включения времени t в качестве независимой переменной в модель регрессии, что позволяет зафиксировать воздействие фактора t. Достоинством такого подхода является использование всей имеющейся выборки в отличие от метода последовательных разностей, который приводит к потере некоторого числа наблюдений.

Рассмотрим, например, модель вида:

y_t =  + ₁x_t + ₂t + _t,

которая относится к моделям c включенным фактором времени. Параметры модели определяются обычным МНК.

Пример. Потребительские расходы и доходы населения (тыс. у. е.) за ряд лет характеризуются следующими данными (табл. 5.13).

Таблица 5.13

Показатель	Год
	1	2	3	4	5	6	7	8	9
Потребительские расходы	46	50	54	59	62	67	75	86	100
Доходы	59	63	64	66	71	78	89	101	114

---