ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 366
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2.1. Основные цели и задачи прикладного корреляционно-регрессионного анализа
2.2. Постановка задачи регрессии
2.4. Коэффициент корреляции, коэффициент детерминации, корреляционное отношение
3. Классическая линейная модель множественной регрессии
3.2. Оценивание коэффициентов КЛММР
модели решается на 1, 2, 3 этапах моделирования и включает в себя:
Этапы 4, 5 и 6 сопровождаются процедурой калибровкимодели, которая заключается в переборе большого числа вариантов, обусловленных наличием «нормативных» ограничений, определенных содержательным смыслом анализируемых связей и определенной нечеткостью (неполнотой) статистической информации. Калибровка модели - трудоемкая процедура, что связано с многократными «вычислительными прогонами» модели.
Наиболее распространенными в эконометрическом моделировании являются следующие образующие четыре группы методы:
Применение этих методов делает возможным построение следующих типов эконометрических моделей:
1. Регрессионные модели с одним уравнением.
В таких моделях зависимая (объясняемая) переменная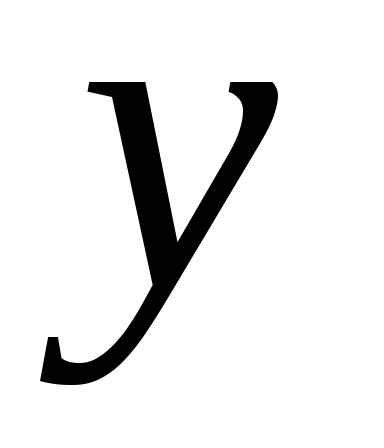 представляется в виде функции
представляется в виде функции
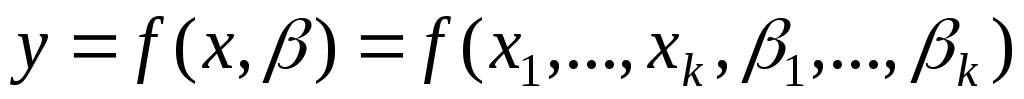 ,
,
где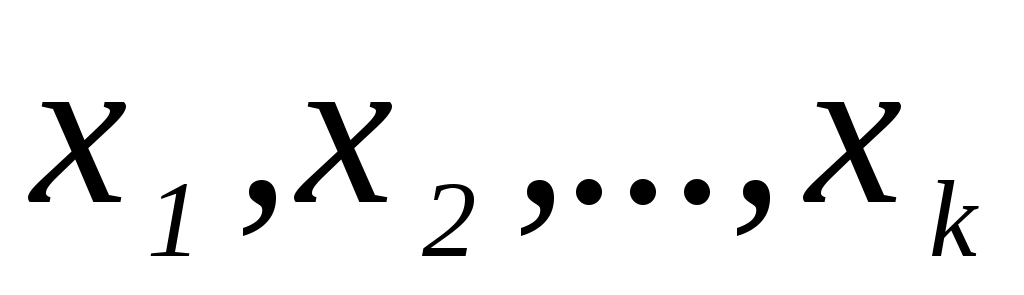 - независимые (объясняющие) переменные,
- независимые (объясняющие) переменные,
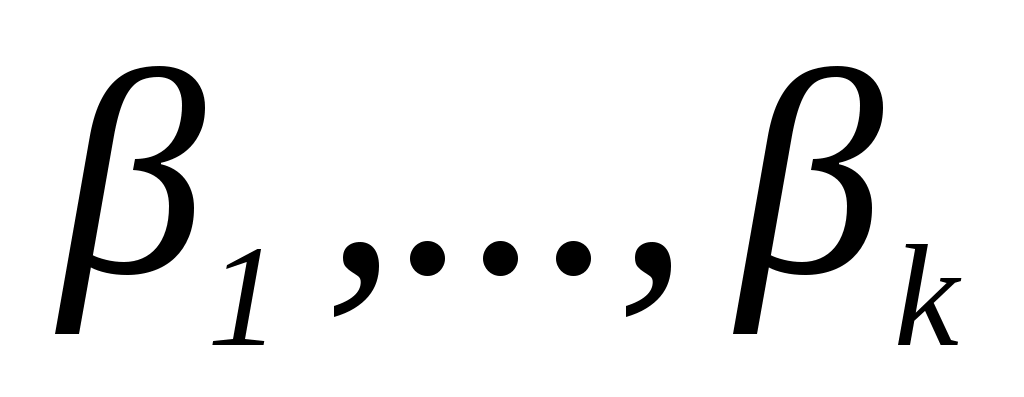 - параметры.
- параметры.
В зависимости от вида функции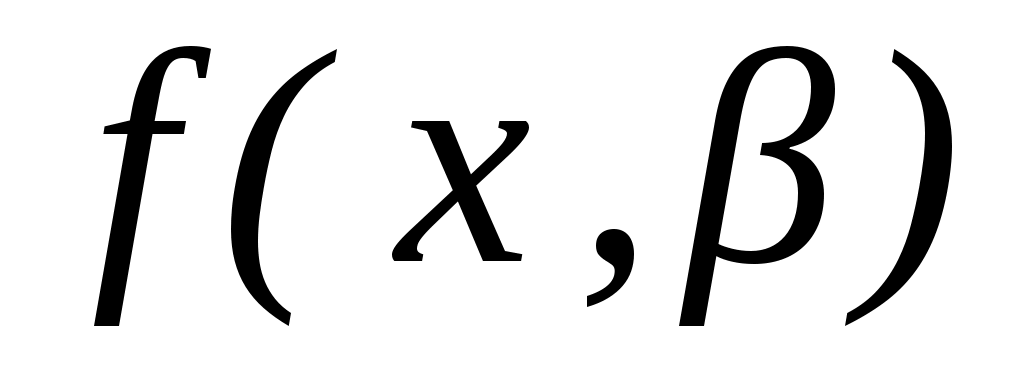 модели делятся на линейные и нелинейные.
модели делятся на линейные и нелинейные.
Например, можно исследовать уровень дохода семьи как функцию от ряда ее экономических и социально-демографических характеристик (наличие и количество работников в семье, наличие и количество детей и прочих иждивенцев, уровень образования и квалификации главы семьи и т.д.).
2. Модели временных рядов.
К этому классу относятся модели:
где t – время,
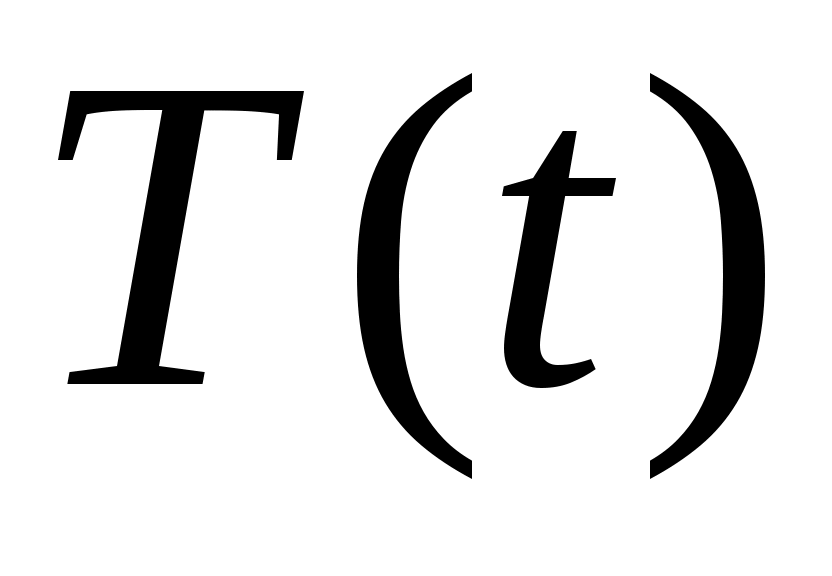 - временной тренд заданного параметрического вида (например, линейный
- временной тренд заданного параметрического вида (например, линейный 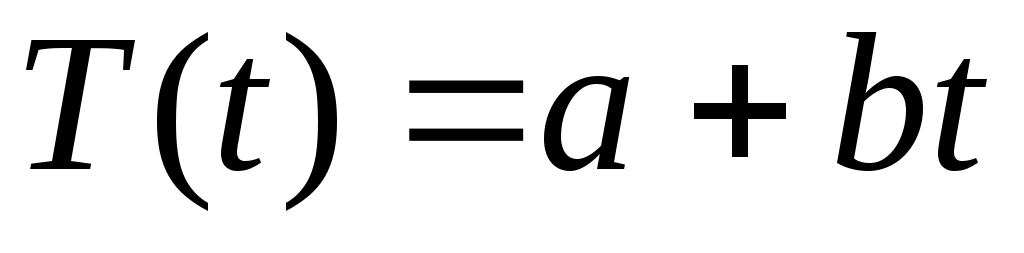 ),
),
- случайная (стохастическая) компонента;
где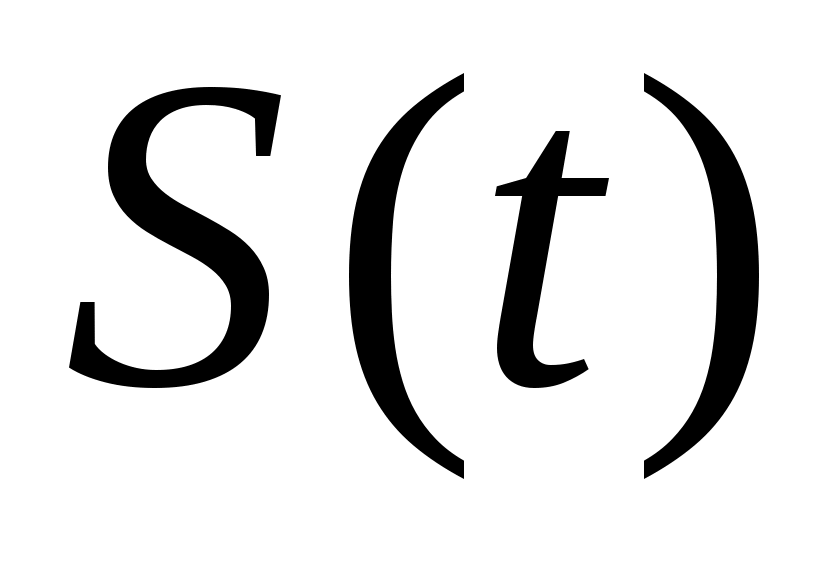 - периодическая (сезонная) компонента,
- периодическая (сезонная) компонента,
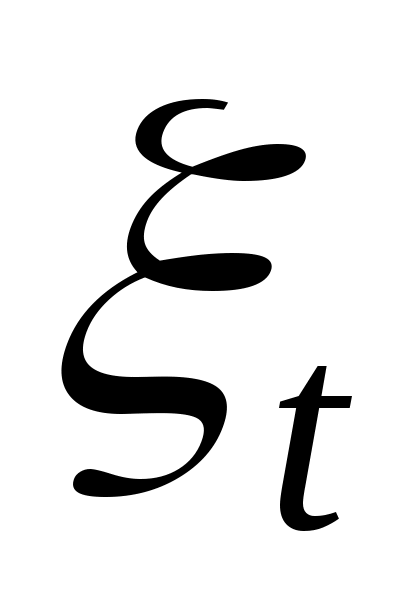 - случайная (стохастическая) компонента.
- случайная (стохастическая) компонента.
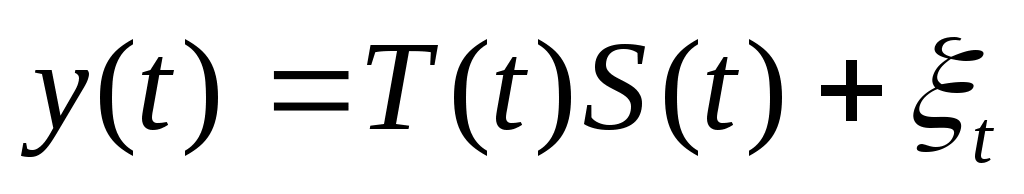 (мультипликативная)
(мультипликативная)
где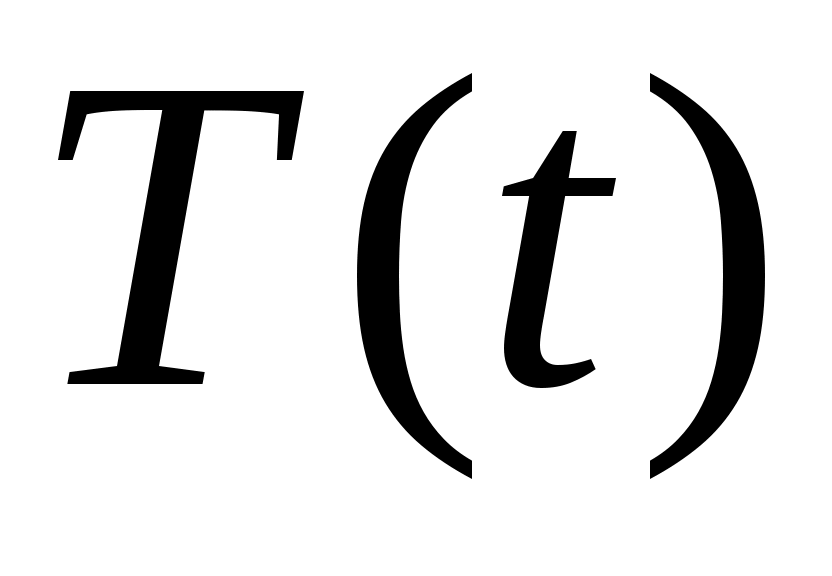 - временной тренд заданного параметрического вида,
- временной тренд заданного параметрического вида,
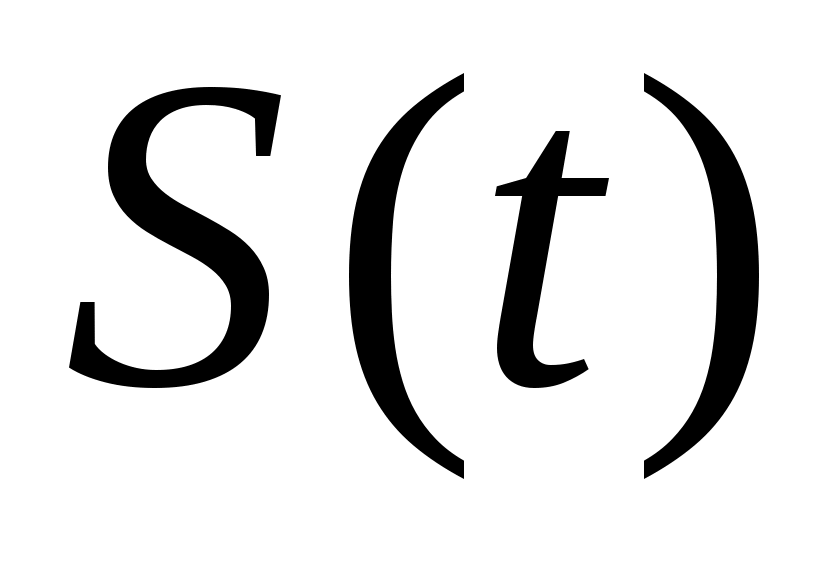 - периодическая (сезонная) компонента,
- периодическая (сезонная) компонента,
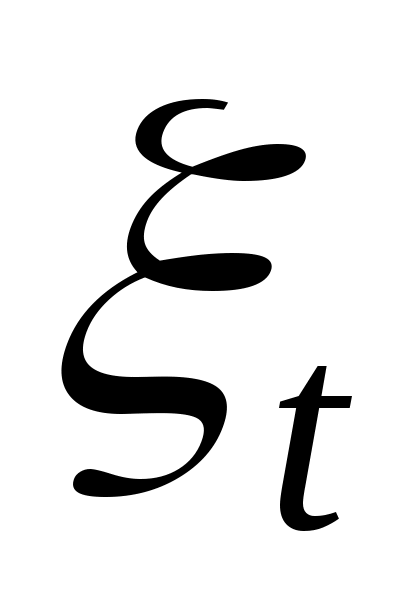 - случайная (стохастическая) компонента.
- случайная (стохастическая) компонента.
Кроме того, существуют модели временных рядов, в которых присутствует циклическая компонента, формирующая изменения анализируемого признака, обусловленные действием долговременных циклов экономической, демографической или астрофизической природы (волны Кондратьева, циклы солнечной активности и т.д.).
Модели временных рядов могут применяться для изучения и прогнозирования объема продаж туристических путевок, спроса на железнодорожные и авиабилеты, при краткосрочном прогнозировании процентных ставок и т.д.
3. Системы одновременных уравнений.
Эти модели описываются системами уравнений. Системы могут состоять из тождеств и регрессионных уравнений, каждое из которых, кроме объясняющих переменных, может включать в себя объясняемые переменные из других уравнений системы. Системы одновременных уравнений требуют сложного математического аппарата и могут быть использованы для моделей национальной экономики.
Ярким примером системы одновременных уравнений служит модель спроса и предложения. Пусть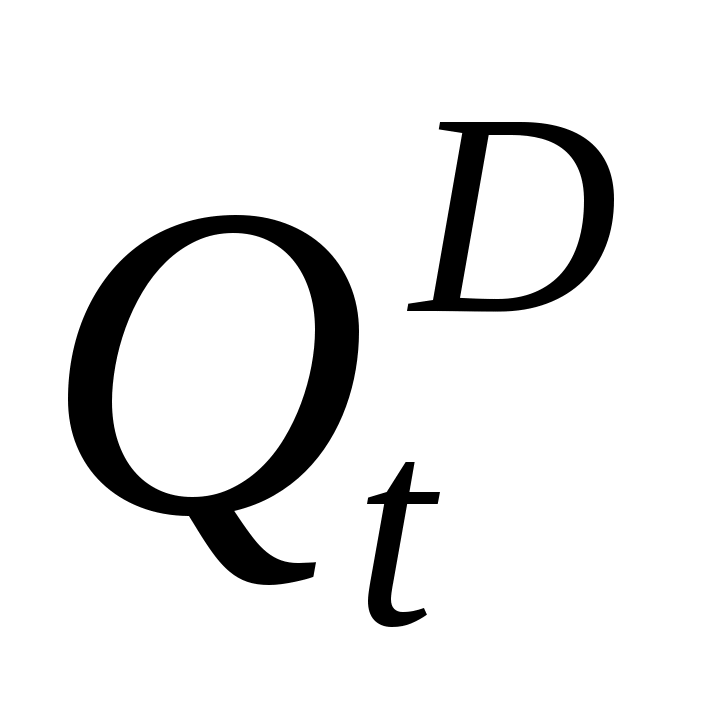 - спрос на товар в момент времени t,
- спрос на товар в момент времени t, 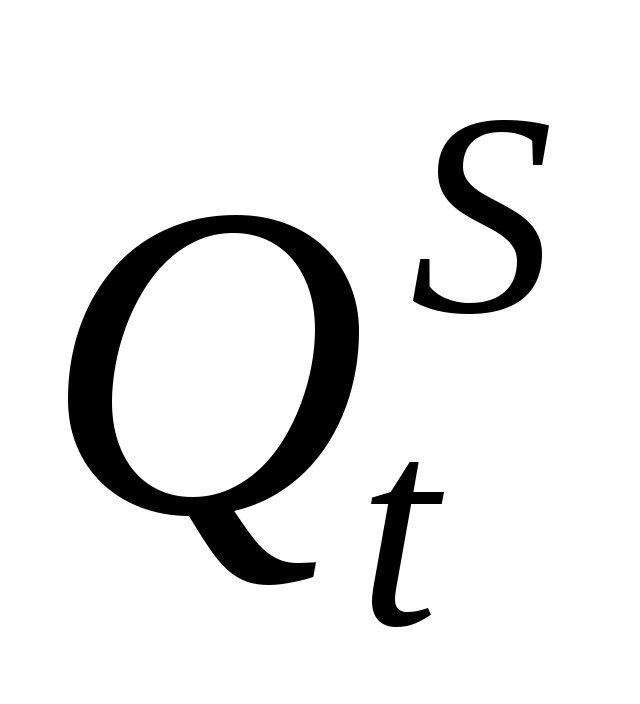 - предложение товара в момент времени t,
- предложение товара в момент времени t, 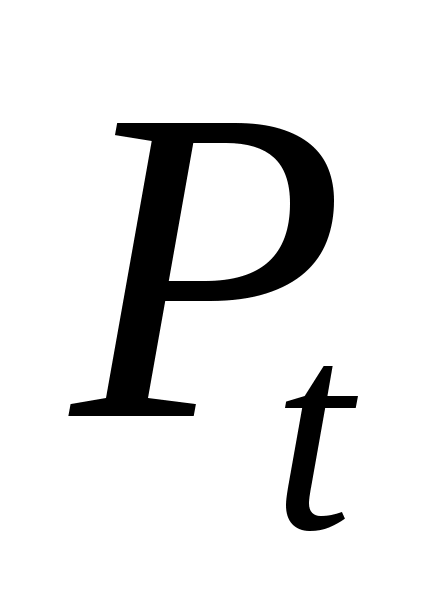 - цена на товар в момент времени t, Yt – доход в момент t.
- цена на товар в момент времени t, Yt – доход в момент t.
Составим систему уравнений "спрос – предложение":
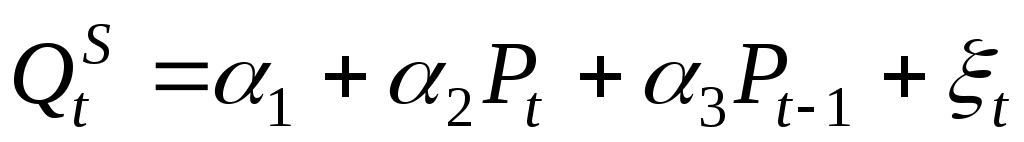 (предложение),
(предложение),
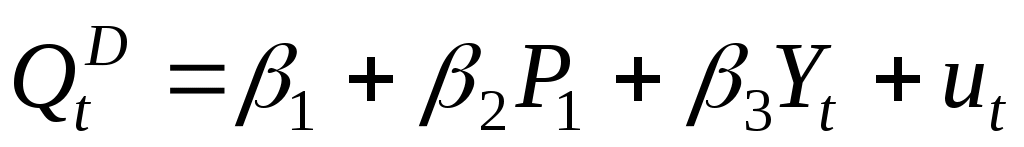 (спрос),
(спрос),
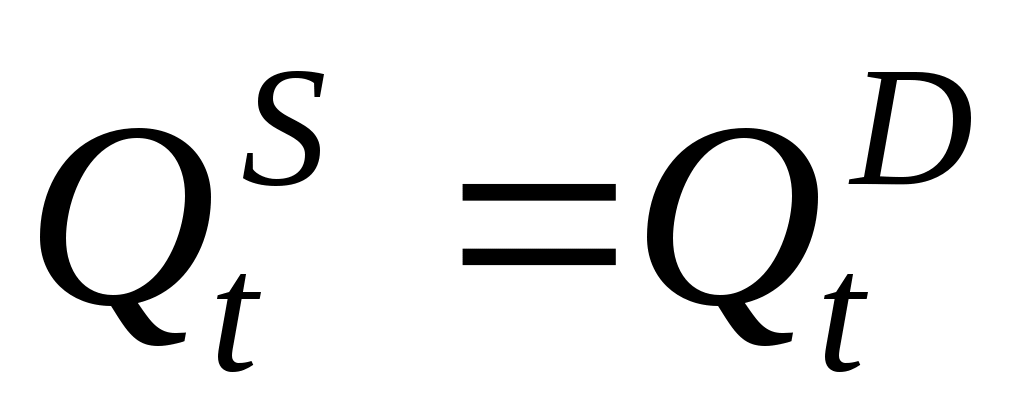 (равновесие).
(равновесие).
Цена товара Pt и спрос на товар определяются из уравнений модели, то есть являются эндогенными переменными. Объясняющими переменными в данной модели являются доход Ytи значение цены товара в предыдущий момент времени
определяются из уравнений модели, то есть являются эндогенными переменными. Объясняющими переменными в данной модели являются доход Ytи значение цены товара в предыдущий момент времени 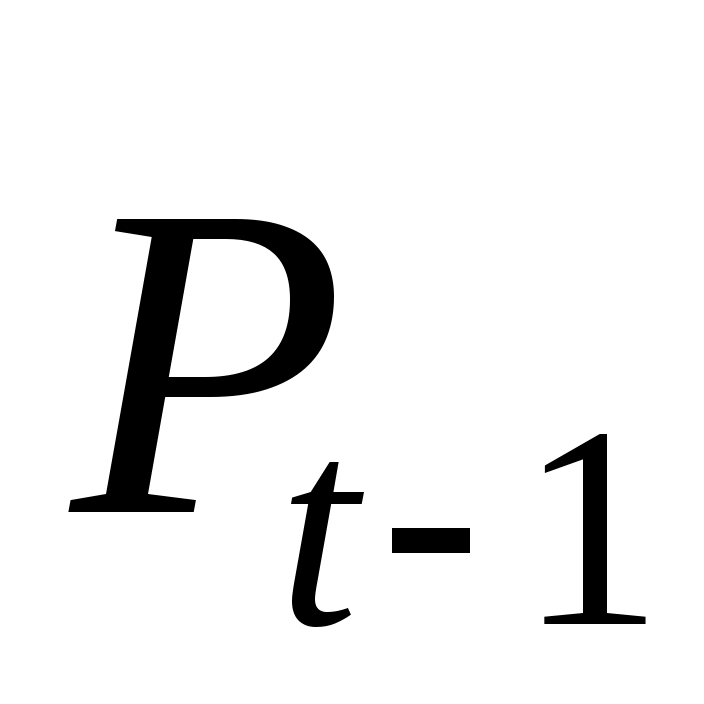 .
.
Для эконометрического моделирования используются данные следующих трех типов.
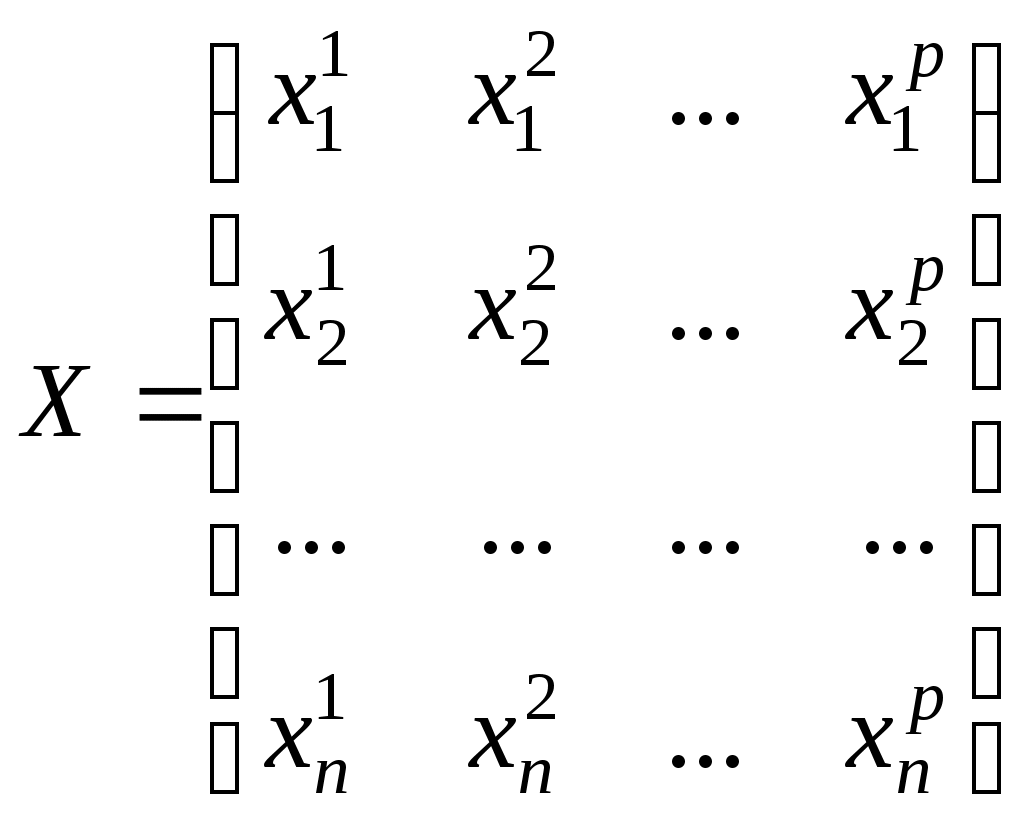 .
.
Такой тип данных называется пространственной выборкой или данными поперечного среза (cross-section data). Такие данные не имеют временного параметра, и порядок их следования не существенен. Пример: финансовые показатели работы предприятий за истекший год.
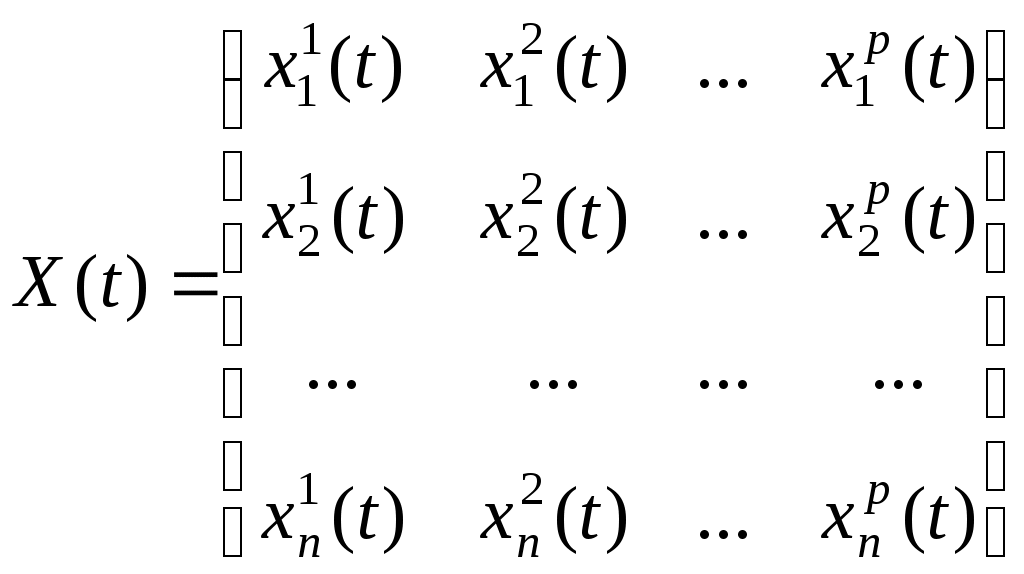 .
.
Такие данные называются панельными, или пространственно-временной выборкой (panel data). Данные сочетают в себе свойства как временных рядов, так и данных поперечного сечения. Как правило, значение T мало. Пример: показатели социально-экономического состояния домохозяйств за три года.
Рассмотрим некоторый экономический объект (процесс, явление, систему) и выделим только две переменные, характеризующие объект. Обозначим переменные буквами Y и X. Будем предполагать, что независимая (объясняющая) переменная Xоказывает воздействие на значения переменной Y, которая, таким образом, является зависимой переменной, т.е. имеет место зависимость:
Y=f(X). (2.1)
Зависимость (2.1) можно рассматривать с целью установления самого факта наличия или отсутствия значимой связи между Y и X, можно преследовать цель прогнозирования неизвестных значений Y по известным значениям X, наконец возможно выявление причинно-следственных связей между X и Y.
При изучении взаимосвязи между переменными Y и X следует, прежде всего, установить тип зависимости (природу анализируемых переменных Y и X). Возможны следующие ситуации:
Будем предполагать наличие второй из указанных ситуаций. Регрессионный анализ является инструментом решения следующих основных задач:
1. Для любых значений объясняющей переменной X построить наилучшие по некоторому критерию оценки для неизвестной функции f(X).
2. По заданным значениям объясняющей переменной X построить наилучший по некоторому критерию прогноз для неизвестного значения результирующей переменной
-
определение конечных целей моделирования (прогноз, имитация сценариев развития анализируемой системы, управление); -
определение списка экзогенных и эндогенных переменных; -
определение состава анализируемой системы уравнений и тождеств и соответственно списка предопределенных переменных; -
формулировка исходных предпосылок и априорных ограничений относительно стохастической природы остатков (рассмотрение проблемы гомоскедастичности).
Этапы 4, 5 и 6 сопровождаются процедурой калибровкимодели, которая заключается в переборе большого числа вариантов, обусловленных наличием «нормативных» ограничений, определенных содержательным смыслом анализируемых связей и определенной нечеткостью (неполнотой) статистической информации. Калибровка модели - трудоемкая процедура, что связано с многократными «вычислительными прогонами» модели.
Наиболее распространенными в эконометрическом моделировании являются следующие образующие четыре группы методы:
-
классическая линейная модель множественной регрессии (КЛММР) и классический метод наименьших квадратов (МНК); -
обобщенная КЛММР и обобщенный МНК; -
методы статистического анализа временных рядов; -
методы анализа систем одновременных эконометрических уравнений.
Применение этих методов делает возможным построение следующих типов эконометрических моделей:
1. Регрессионные модели с одним уравнением.
В таких моделях зависимая (объясняемая) переменная
где
В зависимости от вида функции
Например, можно исследовать уровень дохода семьи как функцию от ряда ее экономических и социально-демографических характеристик (наличие и количество работников в семье, наличие и количество детей и прочих иждивенцев, уровень образования и квалификации главы семьи и т.д.).
2. Модели временных рядов.
К этому классу относятся модели:
-
тренда: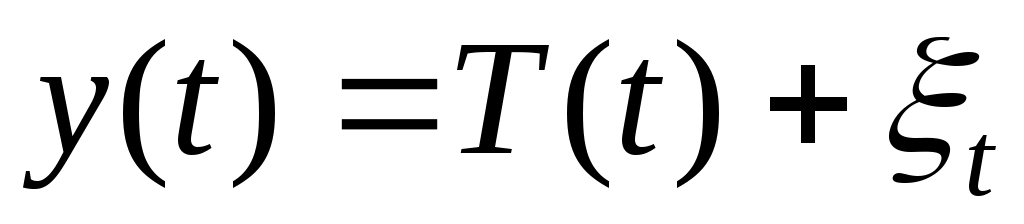 ,
,
где t – время,
- случайная (стохастическая) компонента;
-
сезонности: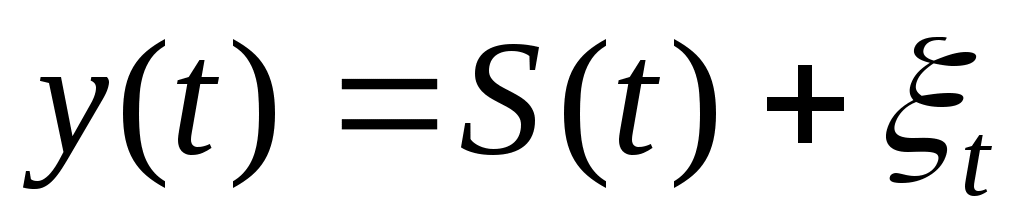 ,
,
где
-
тренда и сезонности: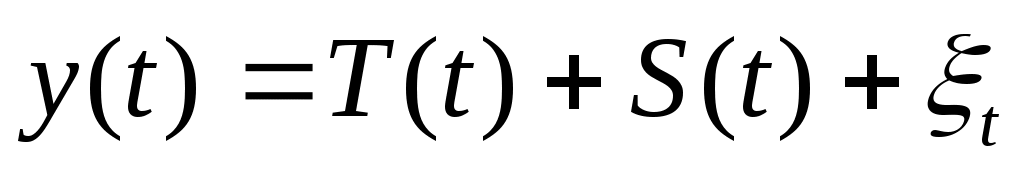 (аддитивная) или
(аддитивная) или
где
Кроме того, существуют модели временных рядов, в которых присутствует циклическая компонента, формирующая изменения анализируемого признака, обусловленные действием долговременных циклов экономической, демографической или астрофизической природы (волны Кондратьева, циклы солнечной активности и т.д.).
Модели временных рядов могут применяться для изучения и прогнозирования объема продаж туристических путевок, спроса на железнодорожные и авиабилеты, при краткосрочном прогнозировании процентных ставок и т.д.
3. Системы одновременных уравнений.
Эти модели описываются системами уравнений. Системы могут состоять из тождеств и регрессионных уравнений, каждое из которых, кроме объясняющих переменных, может включать в себя объясняемые переменные из других уравнений системы. Системы одновременных уравнений требуют сложного математического аппарата и могут быть использованы для моделей национальной экономики.
Ярким примером системы одновременных уравнений служит модель спроса и предложения. Пусть
Составим систему уравнений "спрос – предложение":
Цена товара Pt и спрос на товар
Для эконометрического моделирования используются данные следующих трех типов.
-
Предположим, что мы располагаем результатами регистрации значений переменных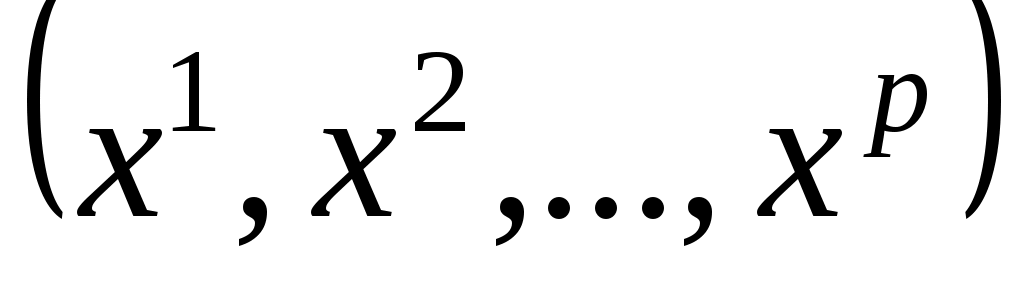 на n статистически обследованных объектах. Так что если i – номер обследованного объекта, то имеющиеся исходные статистические данные состоят из n строк вида
на n статистически обследованных объектах. Так что если i – номер обследованного объекта, то имеющиеся исходные статистические данные состоят из n строк вида 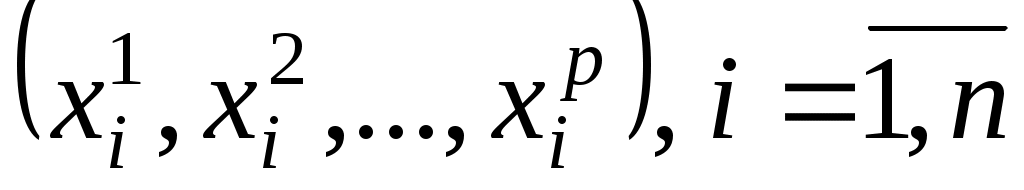 , где
, где 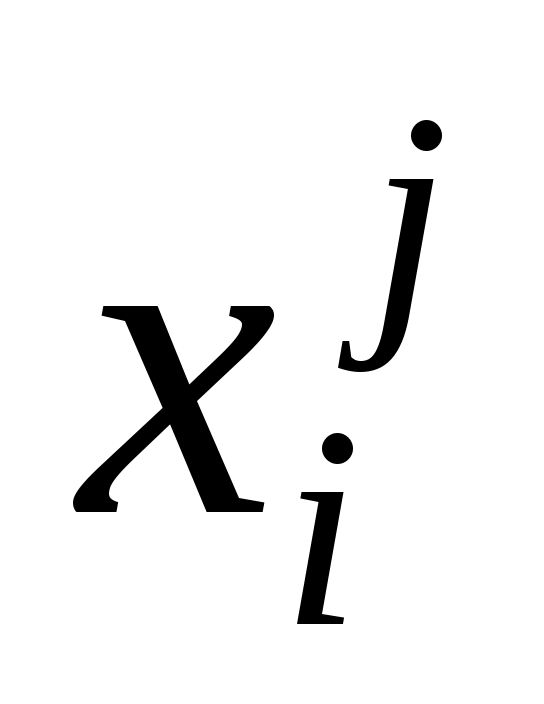 - значение j переменной, зарегистрированное на i обследованном объекте. То есть данные могут быть представлены в виде матрицы np:
- значение j переменной, зарегистрированное на i обследованном объекте. То есть данные могут быть представлены в виде матрицы np:
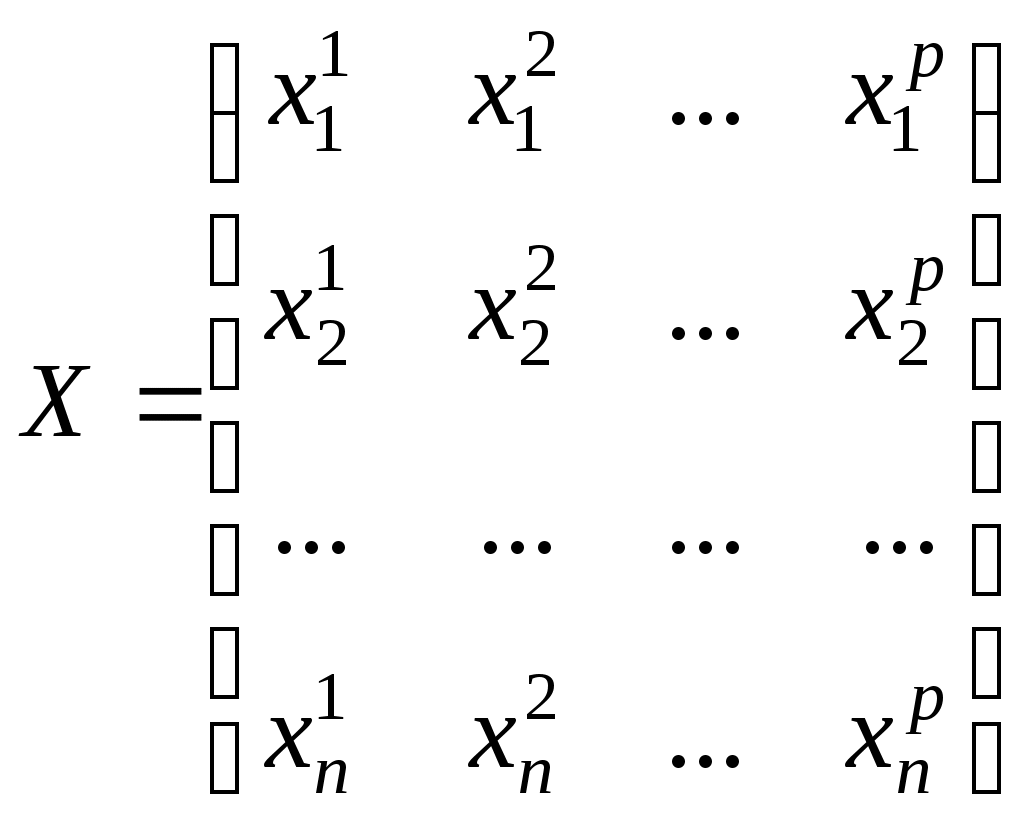 .
.Такой тип данных называется пространственной выборкой или данными поперечного среза (cross-section data). Такие данные не имеют временного параметра, и порядок их следования не существенен. Пример: финансовые показатели работы предприятий за истекший год.
-
Предположим, что данные регистрируются на одном и том же объекте, но в разные периоды времени. Тогда аналогом i будет номер периода времени, к которому привязаны соответствующие данные, а n будет общим числом периодов времени. Такие данные называются временнóй выборкой, или временными рядами данных (time series data), или данными продольного среза. Для таких данных существенен порядок следования значений переменных. Пример: финансовые показатели предприятия за последние несколько лет. -
Наконец, предположим, что отслеживается каждый из n объектов в течение T периодов времени. То есть имеем последовательность матриц вида X, отнесенных к моментам времени 1,2,…,Т:
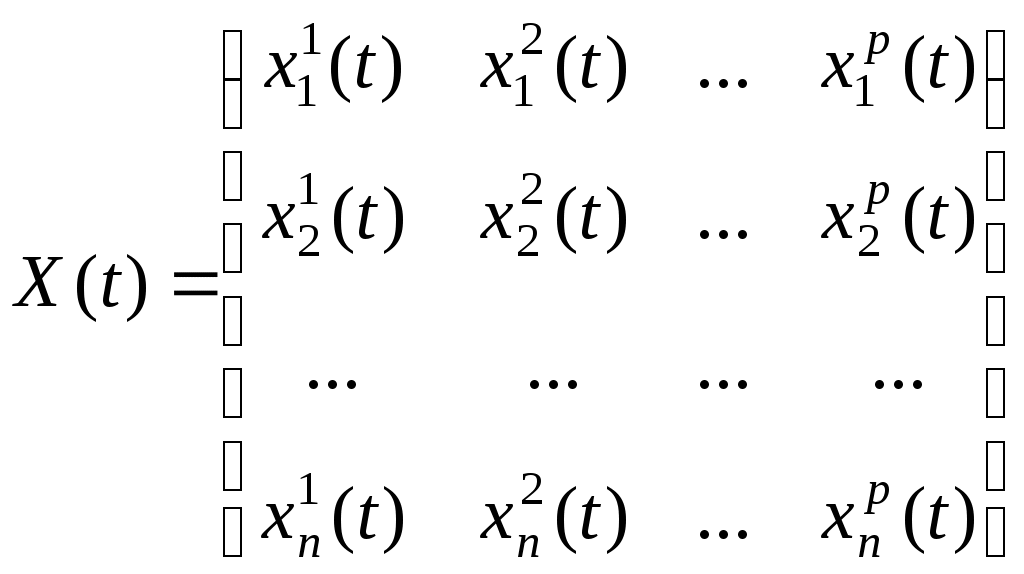 .
.Такие данные называются панельными, или пространственно-временной выборкой (panel data). Данные сочетают в себе свойства как временных рядов, так и данных поперечного сечения. Как правило, значение T мало. Пример: показатели социально-экономического состояния домохозяйств за три года.
2. Парная регрессия
2.1. Основные цели и задачи прикладного корреляционно-регрессионного анализа
Рассмотрим некоторый экономический объект (процесс, явление, систему) и выделим только две переменные, характеризующие объект. Обозначим переменные буквами Y и X. Будем предполагать, что независимая (объясняющая) переменная Xоказывает воздействие на значения переменной Y, которая, таким образом, является зависимой переменной, т.е. имеет место зависимость:
Y=f(X). (2.1)
Зависимость (2.1) можно рассматривать с целью установления самого факта наличия или отсутствия значимой связи между Y и X, можно преследовать цель прогнозирования неизвестных значений Y по известным значениям X, наконец возможно выявление причинно-следственных связей между X и Y.
При изучении взаимосвязи между переменными Y и X следует, прежде всего, установить тип зависимости (природу анализируемых переменных Y и X). Возможны следующие ситуации:
-
Y и X являются неслучайными переменными, т.е. значения Y строго зависят только от соответствующих значений X и полностью ими определяются. В этом случае говорят о функциональной зависимости, когда Y является некоторой функцией от переменной X и верна модель (2.1). Пример: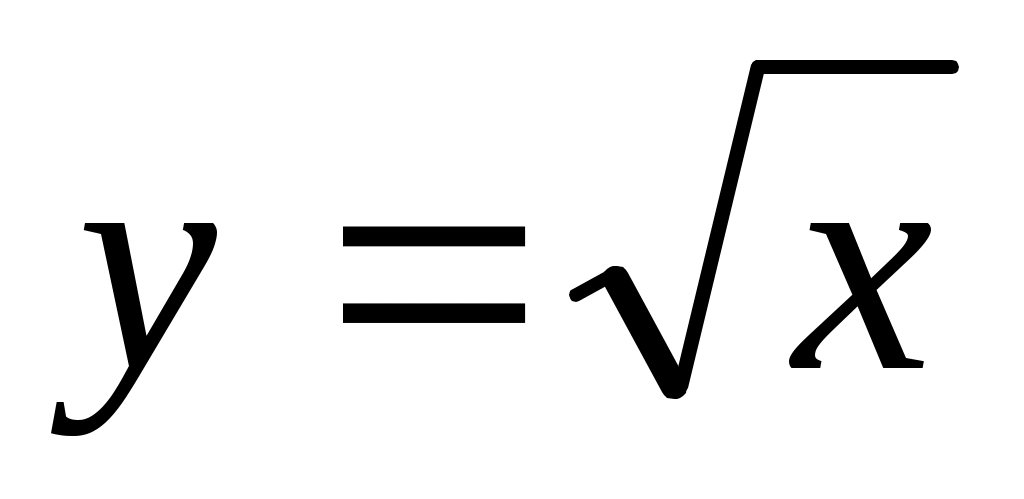 .
. -
Y является случайной переменной, а X– неслучайной. В этом случае считают, что между переменными имеет место регрессионная зависимость. То есть верна модель Y=f(X)+u, где u – величина случайной ошибки. -
Y и X зависят от множества неконтролируемых факторов, так что являются случайными по своей сущности. В этом случае к проблемам построения конкретного вида зависимости между указанными переменными присоединяется проблема исследования тесноты связи между этими переменными. Речь в этом случае идет о корреляционно-регрессионной зависимости между Y и X.
Будем предполагать наличие второй из указанных ситуаций. Регрессионный анализ является инструментом решения следующих основных задач:
1. Для любых значений объясняющей переменной X построить наилучшие по некоторому критерию оценки для неизвестной функции f(X).
2. По заданным значениям объясняющей переменной X построить наилучший по некоторому критерию прогноз для неизвестного значения результирующей переменной