ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 363
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2.1. Основные цели и задачи прикладного корреляционно-регрессионного анализа
2.2. Постановка задачи регрессии
2.4. Коэффициент корреляции, коэффициент детерминации, корреляционное отношение
3. Классическая линейная модель множественной регрессии
3.2. Оценивание коэффициентов КЛММР
Y(X).
3. Пусть известно, что искомая функция зависит от параметра : f(X, ). Требуется построить наилучшую в определенном смысле оценку для неизвестного значения этого параметра.
4. Оценить удельный вес влияния переменной X на результирующий показатель Y.
В следующих разделах параграфа рассмотрим процедуру решения этих задач.
Поставим задачу регрессии Y на X.
Пусть мы располагаем n парами выборочных наблюдений над двумя переменными X и Y:
Функция f(X) называется функцией регрессии Y по X, если она описывает изменение условного среднего значения результирующей переменной Y в зависимости от изменения значений объясняющей переменной X: f(X)=E(Y|X).
Таким образом, имеет место уравнение регрессионной связи между Y и X:
Yi =f(Xi)+ui, i=1,…,n. (2.2)
Присутствие в модели (2.2) случайной "остаточной" компоненты u, также называемой случайным членом, обусловлено следующими причинами:
Мы хотим на основе выборочных наблюдений с учетом дополнительных требований, налагаемых на u, статистически оценить функцию f(X), проверить оптимальность полученной оценки и использовать уравнение для построения прогноза.
Допущения модели. Относительно u
необходимо принять ряд гипотез, известных как условия Гаусса-Маркова:
Это требование состоит в том, что математическое ожидание случайного члена в любом наблюдении должно быть равно нулю. Иногда случайный член будет положительным, иногда отрицательным, но он не должен иметь систематического смещения ни в одном из двух возможных направлений. Свойство непосредственно вытекает из смысла функции регрессии. Возьмем в (2.2) матожидание от обеих частей при фиксированном значении X, получим: E(Y|X) =E(f(X))+E(u), по свойству матожидания E(Y|X) =f(X)+E(u), а поскольку с учетом определения функции регрессии должно быть f(X)=E(Y|X), то необходимо E(u)=0.
Первая строчка означает требование постоянства дисперсии регрессионных остатков (независимость от того, при каких значениях объясняющей переменной производятся наблюдения i), которое называют гомоскедастичностью остатков. Вторая строчка предполагает отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях, которые должны быть абсолютно независимы друг от друга.
Таким образом, задача регрессии имеет вид:
Yi =f(Xi)+ui, i=1,…,n.
а. Eui=0, i=1,…,n. (2.3)
б.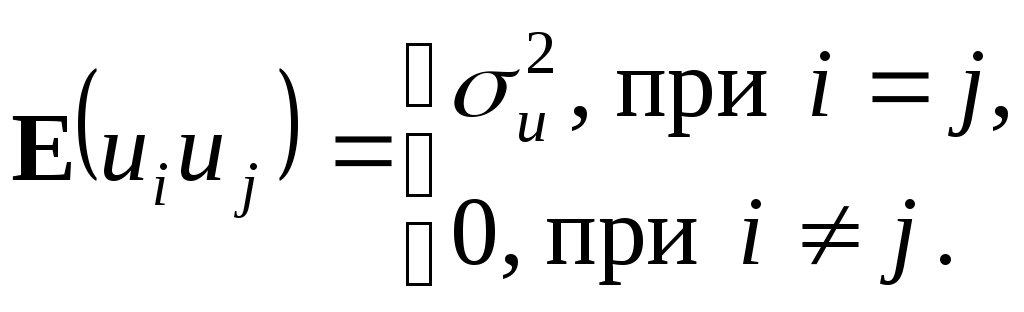
(2.4)
в. X1, …, Xn – неслучайные величины. (2.5)
При выборе вида функции f в (2.2) обычно руководствуются следующими рекомендациями:
2.3. Парная регрессия и метод наименьших квадратов
Будем предполагать в рамках модели (2.2) линейную зависимость между двумя переменными Y и X. Т.е. имеем модель парной регрессии в виде:
Yi =+Xi+ui, i=1,…,n.
а. Eui
=0, i=1,…,n.
б.
в. X1, …, Xn – неслучайные величины.
Предположим, что имеется выборка значений Y и X.
Обозначим арифметические средние (выборочные математические ожидания) для переменных X и Y:
.
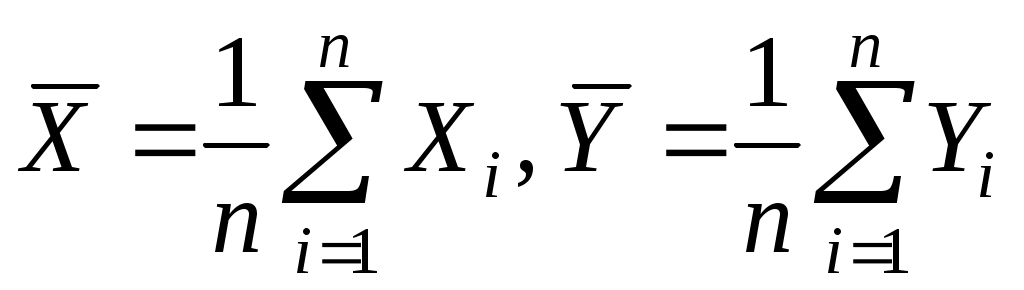Запишем уравнение оцениваемой линии в виде:
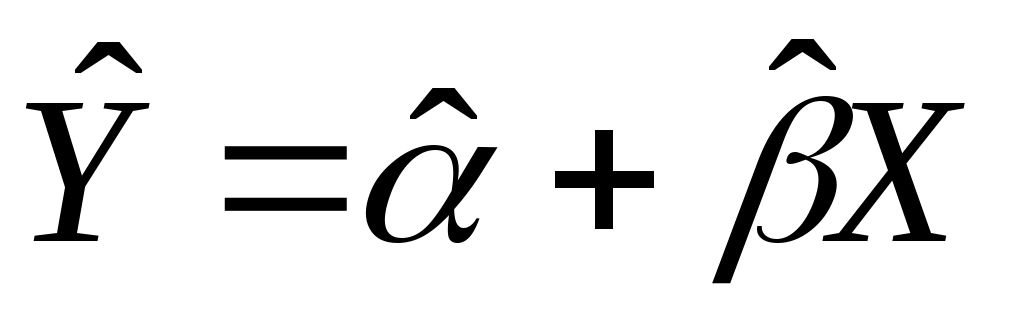, (2.6)
где
и 
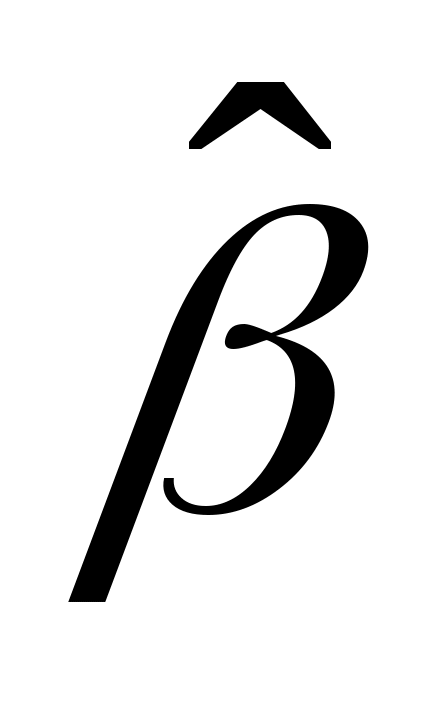- оценки неизвестных параметров и , а 
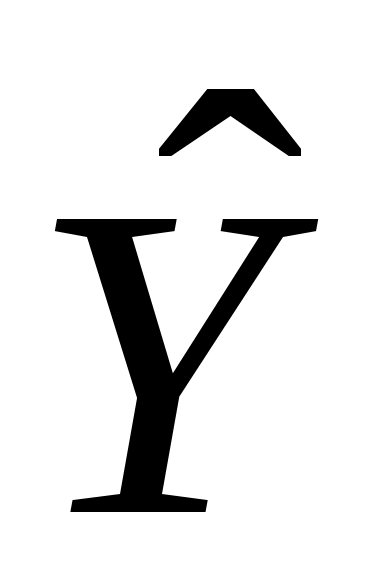- ордината этой линии.
Пусть (Xi, Yi) одна из пар наблюдений. Тогда отклонение этой точки (см. рис. 2.1) от оцениваемой линии будет равно ei=Yi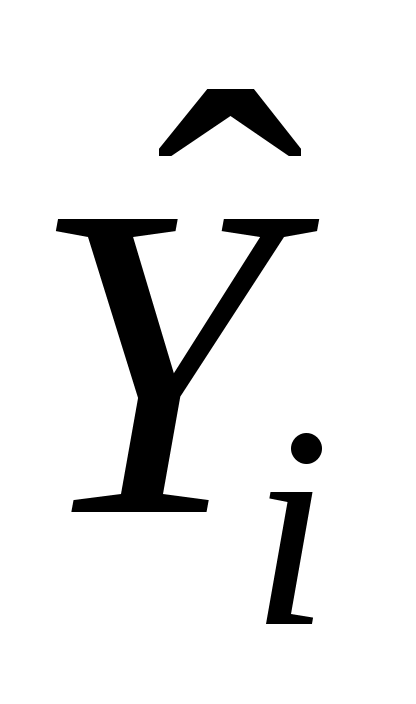 
.
Принцип метода наименьших квадратов (МНК) заключается в выборе таких оценок и 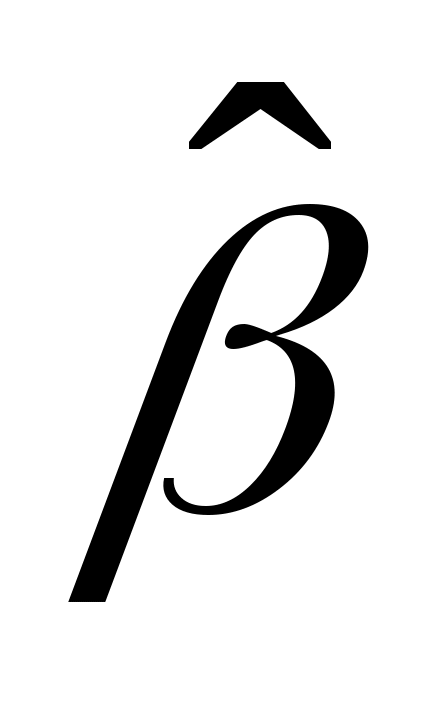, для которых сумма квадратов отклонений для всех точек становится минимальной.
Y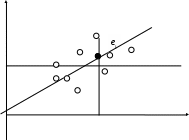
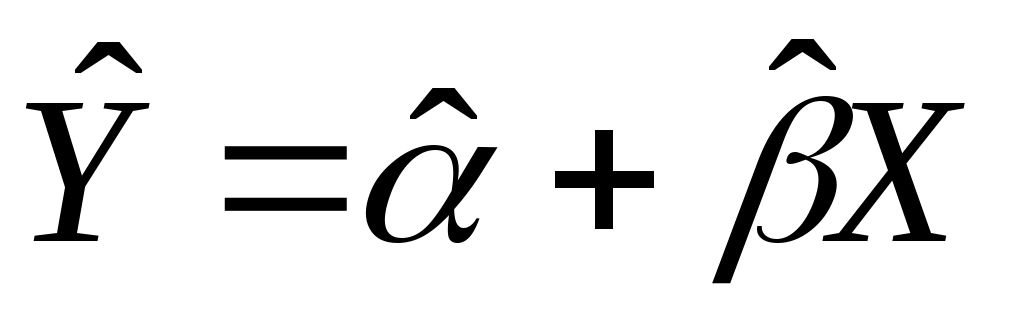
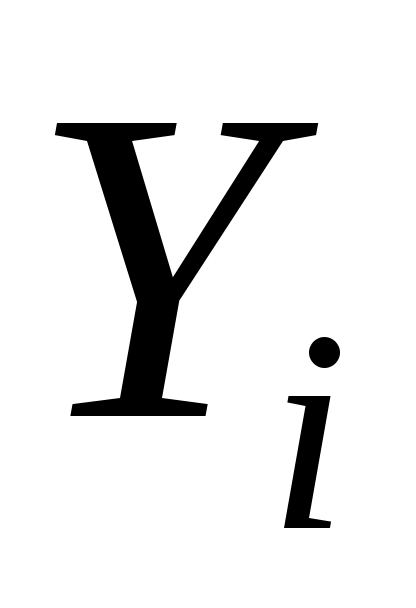
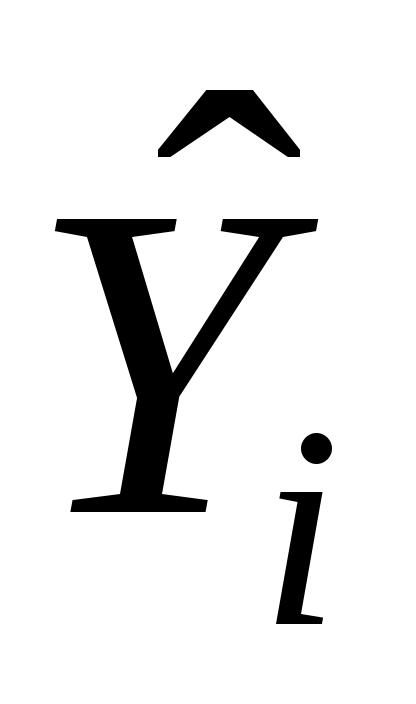
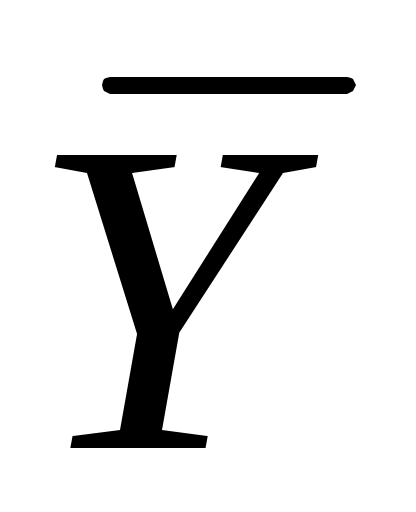
X
Рис. 2.1. Иллюстрация принципа МНК
Необходимым условием для этого служит обращение в нуль частных производных функционала:
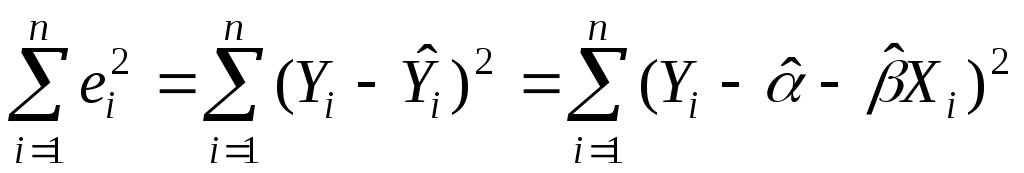
по каждому из параметров. Имеем:
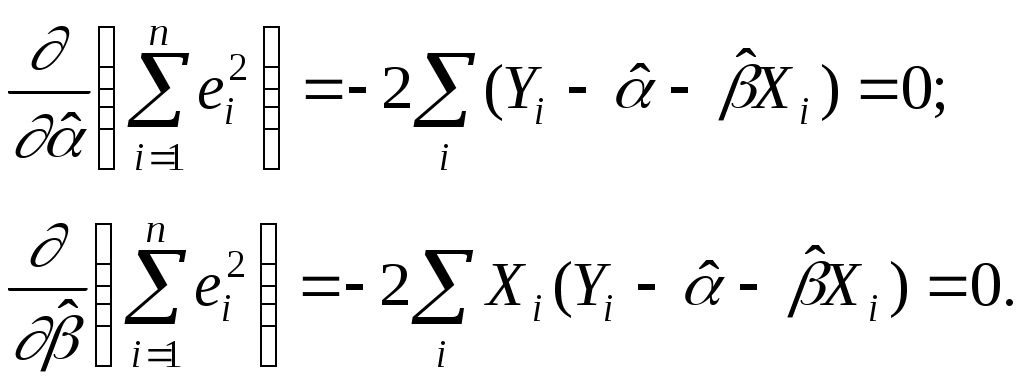
Упростив последние равенства, получим стандартную форму
нормальных уравнений, решение которых дает искомые оценки параметров:
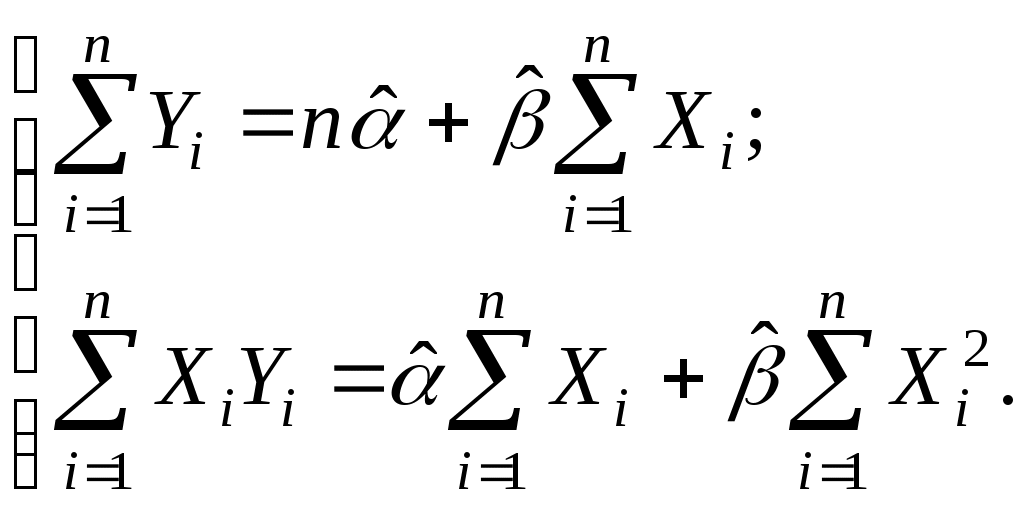(2.7)
Из (2.7) получаем:
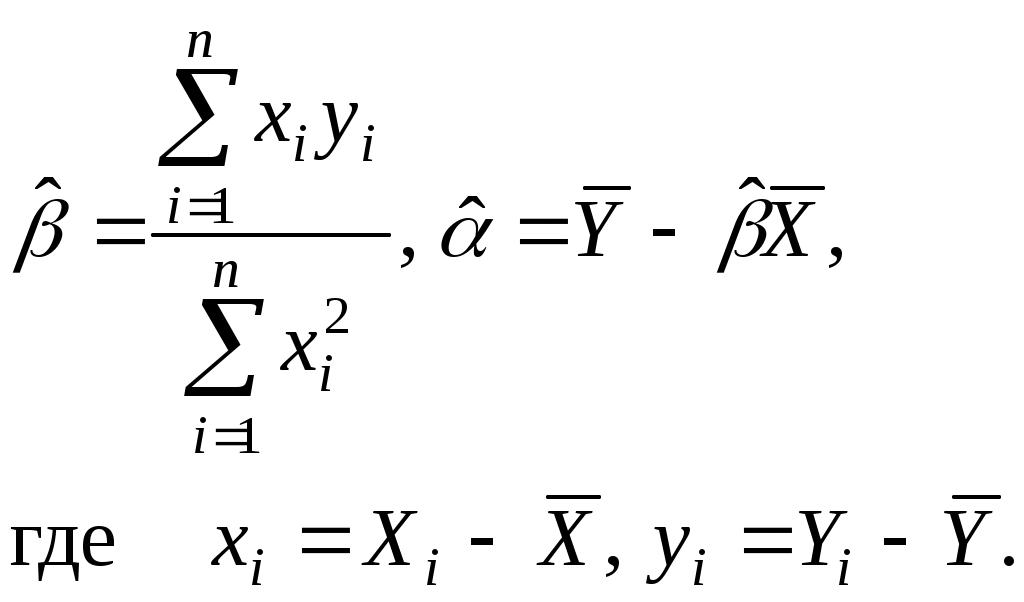(2.8)
Пример. Для иллюстрации вычислений при отыскании зависимости с помощью метода наименьших квадратов рассмотрим пример (табл. 2.1).
Индивидуальное потребление и личные доходы (США, 1954-1965 гг.)
Заметим, что исходные данные должны быть выражены величинами примерно одного порядка. Вычисления удобно организовать, как показано в таблице 2.2. Сначала рассчитываются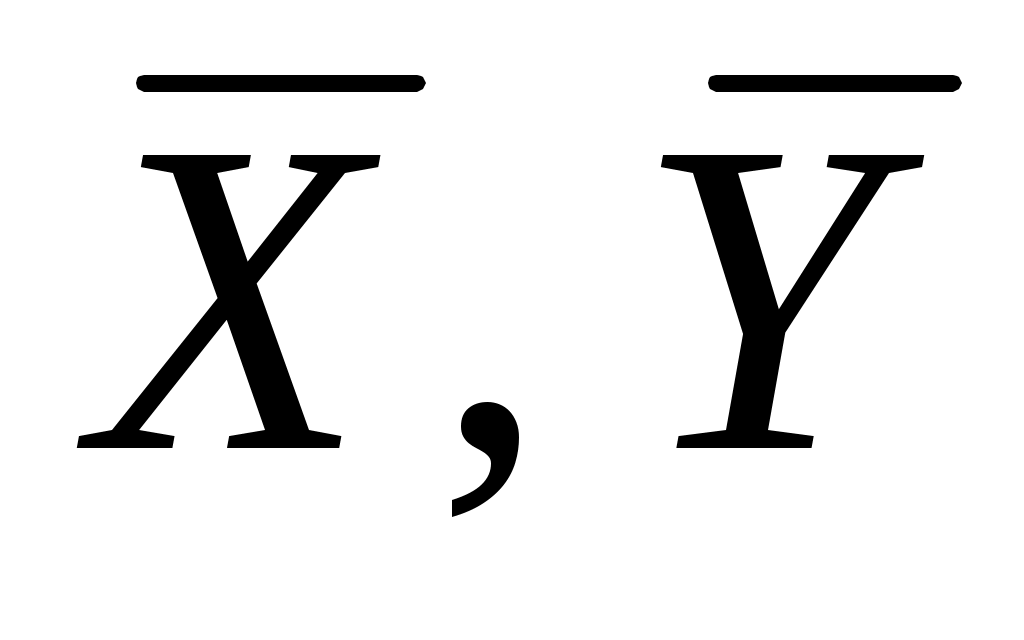
, затем xi, yi. Результаты заносятся в столбцы 3 и 4. Далее определяются xi2, xiyi и заносятся в 5 и 6 столбцы таблицы 2.2. По формулам (2.8) получим искомые значения параметров 
=43145/46510=0,9276; 
=321,75-0,9276.350=-2,91.
Оцененное уравнение регрессии запишется в виде
=-2,91+0,9276X.
Следующая важная проблема состоит в том, чтобы определить, насколько "хороши" полученные оценки и уравнение регрессии. Этот вопрос рассматривается по следующим стадиям исследования: квалифицирование (выяснение условий применимости результатов), определение качества оценок, проверка выполнения допущений метода наименьших квадратов.
Относительно квалифицирования уравнения =-2,91+0,9276X. Оно выражает, конечно, достаточно сильное утверждение. Применять это уравнение для прогнозирования следует очень осторожно. Дело в том, что, даже отвлекаясь от многих факторов, влияющих на потребление, и от систематического изменения дохода по мере варьирования потребления, мы не располагаем достаточно представительной выборкой.
Таблица 2.2
Рабочая таблица расчетов (по данным табл. 2.1)
3. Пусть известно, что искомая функция зависит от параметра : f(X, ). Требуется построить наилучшую в определенном смысле оценку для неизвестного значения этого параметра.
4. Оценить удельный вес влияния переменной X на результирующий показатель Y.
В следующих разделах параграфа рассмотрим процедуру решения этих задач.
2.2. Постановка задачи регрессии
Поставим задачу регрессии Y на X.
Пусть мы располагаем n парами выборочных наблюдений над двумя переменными X и Y:
-
X1,
X2,
. . .
Xn;
Y1,
Y2,
. . .
Yn.
Функция f(X) называется функцией регрессии Y по X, если она описывает изменение условного среднего значения результирующей переменной Y в зависимости от изменения значений объясняющей переменной X: f(X)=E(Y|X).
Таким образом, имеет место уравнение регрессионной связи между Y и X:
Yi =f(Xi)+ui, i=1,…,n. (2.2)
Присутствие в модели (2.2) случайной "остаточной" компоненты u, также называемой случайным членом, обусловлено следующими причинами:
-
Ошибки спецификации. Среди них выделяют невключение важных объясняющих переменных, агрегирование (объединение) переменных, неправильную функциональную спецификацию модели. -
Ошибки измерения. Связаны со сложностью сбора исходных данных и использованием в модели аппроксимирующих переменных для учета факторов, непосредственное измерение которых невозможно. -
Ошибки, связанные со случайностью человеческих реакций. Обусловлены тем, что поведение и непосредственное участие человека в ходе сбора и подготовки данных может быть достаточно непредсказуемым и вносит, таким образом, свой вклад в случайный член.
Мы хотим на основе выборочных наблюдений с учетом дополнительных требований, налагаемых на u, статистически оценить функцию f(X), проверить оптимальность полученной оценки и использовать уравнение для построения прогноза.
Допущения модели. Относительно u
необходимо принять ряд гипотез, известных как условия Гаусса-Маркова:
-
Eui=0, i=1,…,n.
Это требование состоит в том, что математическое ожидание случайного члена в любом наблюдении должно быть равно нулю. Иногда случайный член будет положительным, иногда отрицательным, но он не должен иметь систематического смещения ни в одном из двух возможных направлений. Свойство непосредственно вытекает из смысла функции регрессии. Возьмем в (2.2) матожидание от обеих частей при фиксированном значении X, получим: E(Y|X) =E(f(X))+E(u), по свойству матожидания E(Y|X) =f(X)+E(u), а поскольку с учетом определения функции регрессии должно быть f(X)=E(Y|X), то необходимо E(u)=0.
Первая строчка означает требование постоянства дисперсии регрессионных остатков (независимость от того, при каких значениях объясняющей переменной производятся наблюдения i), которое называют гомоскедастичностью остатков. Вторая строчка предполагает отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях, которые должны быть абсолютно независимы друг от друга.
-
X1, …, Xn – неслучайные величины.
Таким образом, задача регрессии имеет вид:
Yi =f(Xi)+ui, i=1,…,n.
а. Eui=0, i=1,…,n. (2.3)
б.
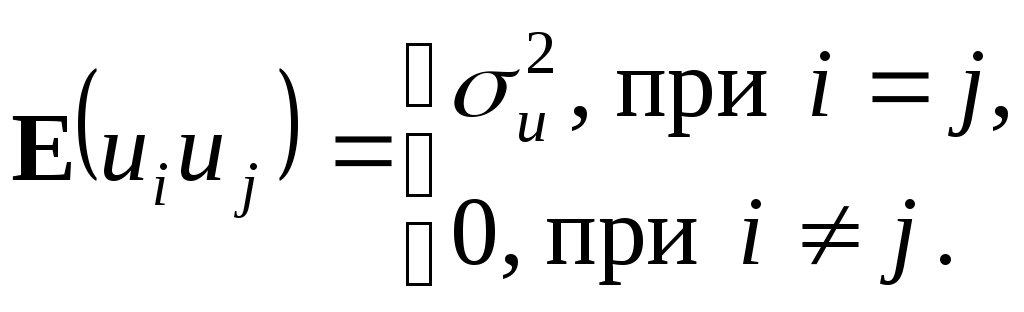(2.4)в. X1, …, Xn – неслучайные величины. (2.5)
При выборе вида функции f в (2.2) обычно руководствуются следующими рекомендациями:
-
используется априорная информация о содержательной экономической сущности анализируемой зависимости – аналитический способ, -
предварительный анализ зависимости с помощью визуализации – графический способ, -
использование различных статистических приемов обработки исходных данных и экспериментальных расчетов.
2.3. Парная регрессия и метод наименьших квадратов
Будем предполагать в рамках модели (2.2) линейную зависимость между двумя переменными Y и X. Т.е. имеем модель парной регрессии в виде:
Yi =+Xi+ui, i=1,…,n.
а. Eui
=0, i=1,…,n.
б.
в. X1, …, Xn – неслучайные величины.
Предположим, что имеется выборка значений Y и X.
Обозначим арифметические средние (выборочные математические ожидания) для переменных X и Y:
.Запишем уравнение оцениваемой линии в виде:
, (2.6)где
и - оценки неизвестных параметров и , а - ордината этой линии.Пусть (Xi, Yi) одна из пар наблюдений. Тогда отклонение этой точки (см. рис. 2.1) от оцениваемой линии будет равно ei=Yi
.Принцип метода наименьших квадратов (МНК) заключается в выборе таких оценок
и , для которых сумма квадратов отклонений для всех точек становится минимальной.Y
X
Рис. 2.1. Иллюстрация принципа МНК
Необходимым условием для этого служит обращение в нуль частных производных функционала:
по каждому из параметров. Имеем:
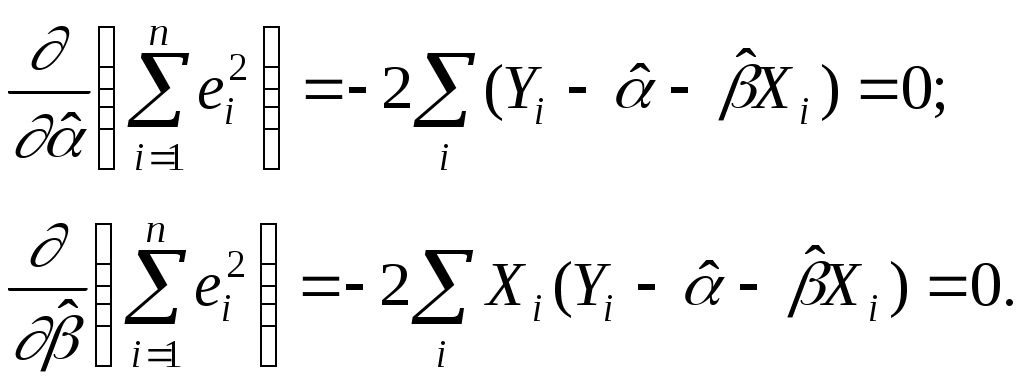
Упростив последние равенства, получим стандартную форму
нормальных уравнений, решение которых дает искомые оценки параметров:
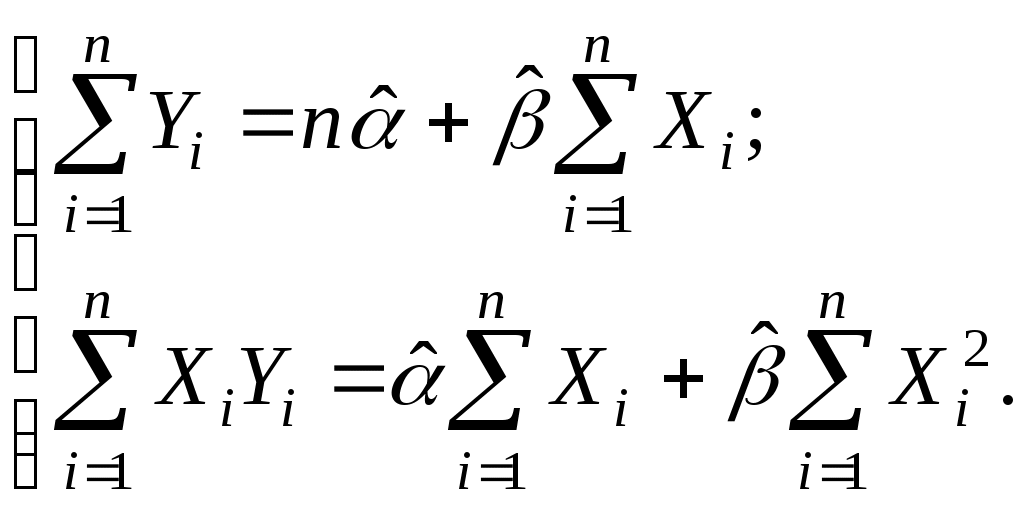(2.7)Из (2.7) получаем:
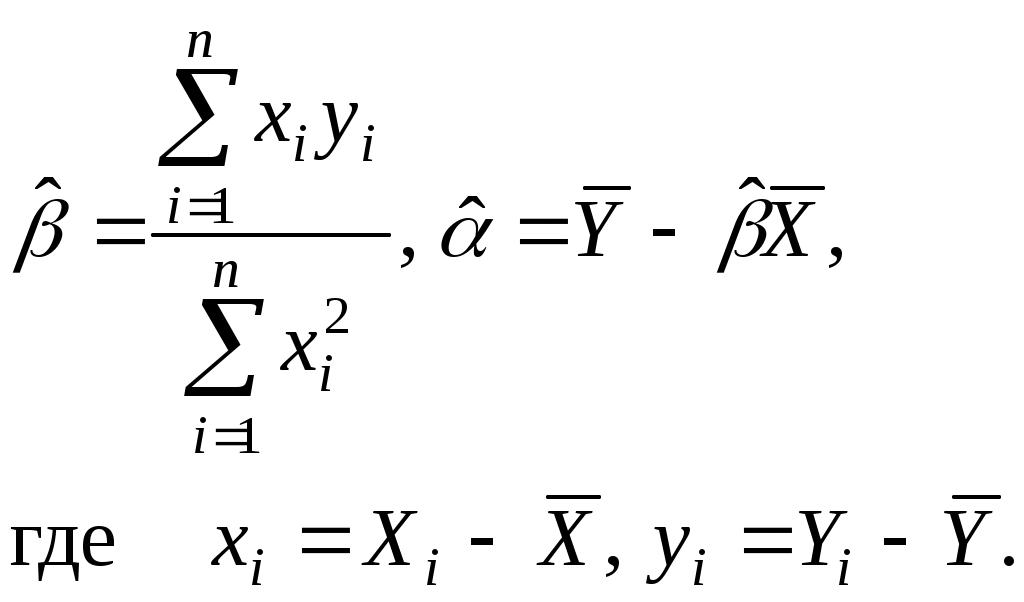(2.8)Пример. Для иллюстрации вычислений при отыскании зависимости с помощью метода наименьших квадратов рассмотрим пример (табл. 2.1).
Таблица 2.1
Индивидуальное потребление и личные доходы (США, 1954-1965 гг.)
| Год | Индивидуальное потребление, млрд. долл. | Личные доходы, млрд. долл. |
| 1954 | 236 | 257 |
| 1955 | 254 | 275 |
| 1956 | 267 | 293 |
| 1957 | 281 | 309 |
| 1958 | 290 | 319 |
| 1959 | 311 | 337 |
| 1960 | 325 | 350 |
| 1961 | 335 | 364 |
| 1962 | 355 | 385 |
| 1963 | 375 | 405 |
| 1964 | 401 | 437 |
| 1965 | 431 | 469 |
Заметим, что исходные данные должны быть выражены величинами примерно одного порядка. Вычисления удобно организовать, как показано в таблице 2.2. Сначала рассчитываются
, затем xi, yi. Результаты заносятся в столбцы 3 и 4. Далее определяются xi2, xiyi и заносятся в 5 и 6 столбцы таблицы 2.2. По формулам (2.8) получим искомые значения параметров =43145/46510=0,9276; =321,75-0,9276.350=-2,91.Оцененное уравнение регрессии запишется в виде
=-2,91+0,9276X. Следующая важная проблема состоит в том, чтобы определить, насколько "хороши" полученные оценки и уравнение регрессии. Этот вопрос рассматривается по следующим стадиям исследования: квалифицирование (выяснение условий применимости результатов), определение качества оценок, проверка выполнения допущений метода наименьших квадратов.
Относительно квалифицирования уравнения
=-2,91+0,9276X. Оно выражает, конечно, достаточно сильное утверждение. Применять это уравнение для прогнозирования следует очень осторожно. Дело в том, что, даже отвлекаясь от многих факторов, влияющих на потребление, и от систематического изменения дохода по мере варьирования потребления, мы не располагаем достаточно представительной выборкой. Таблица 2.2
Рабочая таблица расчетов (по данным табл. 2.1)
| Год | X | Y | x | y | x2 | xy | | ei |
| 1954 | 257 | 236 | -93 | -85,75 | 8649 | 7974,75 | 235,48 | 0,52 |
| 1955 | 275 | 254 | -75 | -67,75 | 5625 | 5081,25 | 252,18 | 1,82 |
| 1956 | 293 | 267 | -57 | -54,75 | 3249 | 3120,75 | 268,88 | -1,88 |
| 1957 | 309 | 281 | -41 | -40,75 | 1681 | 1670,75 | 283,72 | -2,72 |
| 1958 | 319 | 290 | -31 | -31,75 | 961 | 984,25 | 292,99 | -2,99 |
| 1959 | 337 | 311 | -13 | -10,75 | 169 | 139,75 | 309,69 | 1,31 |
| 1960 | 350 | 325 | 0 | 3,25 | 0 | 0 | 321,75 | 3,25 |
| 1961 | 364 | 335 | 14 | 13,25 | 196 | 185,5 | 334,74 | 0,26 |
| 1962 | 385 | 355 | 35 | 33,25 | 1225 | 1163,75 | 354,22 | 0,78 |
| 1963 | 405 | 375 | 55 | 53,25 | 3025 | 2928,75 | 372,77 | 2,23 |
| 1964 | 437 | 401 | 87 | 79,25 | 7569 | 6894,75 | 402,45 | -1,45 |
| 1965 | 469 | 431 | 119 | 109,25 | 14161 | 13000,75 | 432,13 | -1,13 |
| |  =350,00 |  =321,75 | 0 | 0,00 | 46510 | 43145 | =321,75 | 0,00 |