Файл: Курс лекций по дисциплине Эконометрика.doc

Этап 3. Определим компоненту Т. Для этого проведем аналитическое выравнивание ряда (ТЕ) с помощью линейного тренда. Имеем линейный тренд вида:

T = 13,5229+0,7730t.

Стандартная ошибка коэффициента регрессии 0,735. R²=0,97.

Подставляя в уравнение тренда последовательно t= 1,…,20, получим значения тренда для каждого уровня временного ряда (столбец 5, табл. 5.12).

Этап 4. Найдем значения уровней ряда, полученные по мультипликативной модели как (TS) (столбец 6, табл. 5.12).

Этап 5. Рассчитаем абсолютную ошибку как U=y_i-(TS), (столбец 7, табл. 5.12). Качество полученной модели можно проверить, используя сумму квадратов абсолютных ошибок (столбец 8). Общая сумма квадратов абсолютных ошибок равна 21,033. По отношению к сумме квадратов отклонений исходных уровней ряда от его среднего уровня, равной 530,072, эта величина составит 3,9681%:

(21,03378/530,072)100=3,97 %.

Следовательно, мультипликативная модель объясняет 96,03% общей вариации экспорта. 

---

5.6. Модели стационарных и нестационарных временных рядов и их идентификация

Модели авторегрессии порядка p (AutoRegressive - AR(p) models).

Достаточно часто экономические показатели, представленные в виде временного ряда, имеют сложную структуру. Моделирование таких рядов путем построения модели тренда, сезонности и периодической составляющей не приводит к удовлетворительным результатам. Ряд остатков часто имеет статистические закономерности. Наиболее распространенными моделями стационарных рядов являются модели авторегрессии и модели скользящего среднего.

Будем рассматривать класс стационарных временных рядов. Задача состоит в построении модели остатков временного ряда u_t и прогнозирования его значений.

Авторегрессионная модель предназначена для описания стационарных временных рядов. Стационарный процесс удовлетворяет уравнению авторегрессии бесконечного порядка с достаточно быстро убывающими коэффициентами. В частности поэтому авторегрессионная модель достаточно высокого порядка может хорошо аппроксимировать почти любой стационарный процесс. В связи с этим модель авторегрессии часто применяется для моделирования остатков в той или иной параметрической модели, например регрессионной модели или модели тренда.

Модель авторегрессии порядка 1AR(1) (марковский процесс).

Марковскими называются процессы, в которых состояние объекта в каждый следующий момент времени определяется только состоянием в настоящий момент и не зависит от того, каким путем объект достиг этого состояния. В терминах корреляционного анализа для временных рядов марковский процесс можно описать следующим образом: существует статистически значимая корреляционная связь исходного ряда с рядом, сдвинутым на один временной интервал, и отсутствует с рядами, сдвинутыми на два, три и т. д. временных интервала. В идеальном случае эти коэффициенты корреляции равны нулю.

Авторегрессионная модель первого порядка определяется соотношением:

u(t)= u(t-1)+(t) , (5.1)

где  - числовой коэффициент <1, (t) – последовательность случайных величин, образующих «белый шум» (E(

---

(t))=0, E((t)(t+))= ).

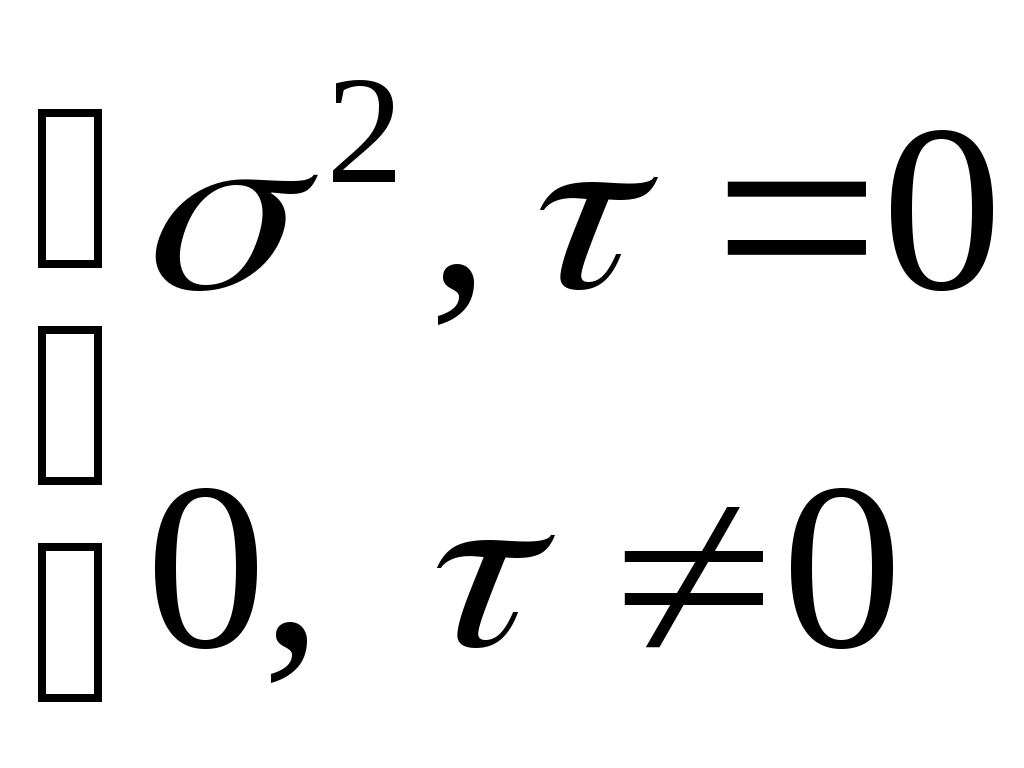Модель (5.1) называется также марковским процессом.

Имеем:

E(u(t))0. (5.2)

r(u(t)u(t))=^. (5.3)

Du(t)=²/(1-²). (5.4)

cov(u(t)u(t))=^Du(t). (5.5)

Из (5.3) следует, что при  близком к единице дисперсия u(t) будет намного больше дисперсии _t. Это значит (учитывая (5.2) =r(u(t)u(t1))=r(1), т.е. параметр  может быть интерпретирован как значение автокорреляции первого порядка), что в случае сильной корреляции соседних значений ряда u(t) ряд слабых возмущений _t будет порождать размашистые колебания остатков u(t).

Условие стационарности ряда (5.1) определяется требованием <1.

Автокорреляционная функция (АКФ) r() марковского процесса определяется соотношением (5.3).

Частная автокорреляционная функция

r_част()=r(u(t)u(t+))  u(t+1)=u(t+2)=…=u(t+-1)=0

может быть вычислена по формуле: r_част(2)=(r(2)-r²(1))/(1-r²(1)). Для второго и выше порядков (см. [1], с. 413, 414) должно быть r_част()=0 =2,3,… . Это удобно использовать для подбора модели (5.1): если вычисленные по оцененным невязкам u(t)=y_t- выборочные частные корреляции статистически незначимо отличаются от нуля при=2,3,…, то использование модели AR(1) для описания случайных остатков не противоречит исходным данным.

Идентификация модели. Требуется статистически оценить параметры  и ² модели (5.1) по имеющимся значениям исходного ряда y_t.

Выделяем неслучайную составляющую и получаем невязки . Находим дисперсию невязок , где (для большинства методов выделения автоматически

---

=0). Далее с учетом (5.2), (5.3) получим формулы для оценки параметров модели (5.1):

,

.

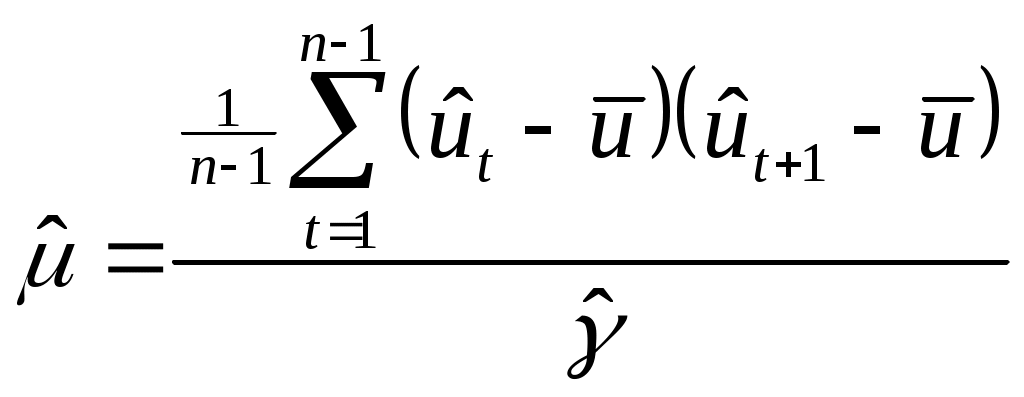Модели авторегрессии р порядка – AR(p) при p2 см. в [1], с. 834-837:

u(t)=₁u(t-1)+₂u(t-2)+…+(t). (5.6)

Пример. График первой разности ряда, хорошо описывающейся моделью AR(1), представлен на рис. 5.1; график выборочной автокорреляционной функции (АКФ) первой разности этого ряда представлен на рис. 5.2. 

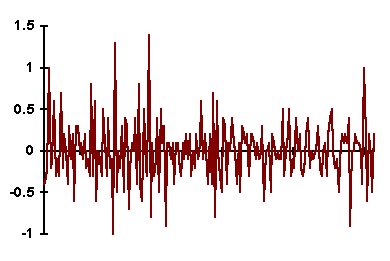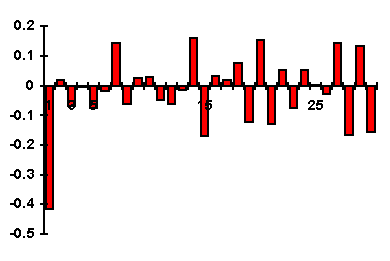Рис. 5.1	Рис. 5.2

---

Модели скользящего среднего порядка q (MovingAverage - MA(q) models).

Часто на показатель в текущий момент времени оказывает воздействие значение показателя в предыдущие моменты. Хотя воздействие отдаленных элементов незначительно, в сумме оно может оказывать существенное влияние на модель. Учесть это воздействие возможно в модели скользящего среднего. Моделирование воздействия всех предшествующих элементов ряда на показатель в текущий момент основано на предпосылке о том, что в ошибках модели за несколько предшествующих периодов сосредоточена информация о всей предыстории ряда.

Моделью скользящего среднего порядка q называется процесс:

u(t)=(t)-₁(t-1)-₂(t-2)-…-_q(t-q). (5.7)

В частности, модели порядка 1 и 2 соответственно имеют вид:

u(t)=(t)-(t-1), (5.8)

u(t)=(t)-₁(t-1)-₂(t-2). (5.9)

Переход от формы (5.6) к форме (5.7) осуществляется с помощью последовательной подстановки в правую часть формулы (5.6) вместо u(t-1), u(t-2), … их выражений, вычисленных по формуле (5.6) для моментов времени t-1, t-2, …. Это означает двойственность в представлении анализируемого временного ряда – две эквивалентные формы линейного процесса - и обратимость AR и MA моделей.

В качестве примера рассмотрим модель скользящего среднего первого порядка – МА(1). Данная модель описывается соотношением (5.8). Можно показать, что стационарность u(t) обеспечивается при любом значении параметра . Модель обратима (представима в виде модели авторегрессии бесконечного порядка) при условии <1.

Автокорреляционная функция:



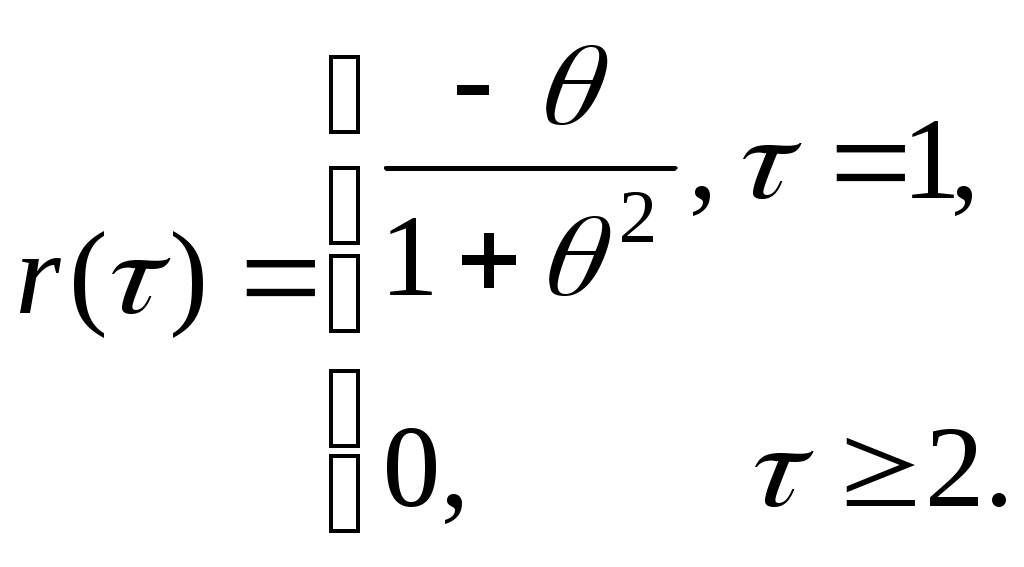
Частная корреляционная функция процесса МА(1), определяющая степень тесноты корреляционной связи между u(t) и u(t), =1,2, … при фиксированных значениях всех промежуточных элементов этого ряда задается выражением:

.

Идентификация модели МА(1). Требуется статистически оценить параметры  и ² модели (5.8) по имеющимся значениям исходного ряда y_t. Выделяем неслучайную составляющую

---