Файл: Курс лекций по дисциплине Эконометрика.doc

Полученное уравнение =-2,91+0,9276X можно использовать для расчета точечного прогноза, в том числе и на ретроспективу. Подставляя последовательно значения X из второго столбца табл. 2.2 в уравнение =-2,91+0,9276X, получим предпоследний столбец табл. 2.2 для прогнозных значений . Ошибка прогноза вычисляется по формуле e_i=Y_i  и дана в последнем столбце рабочей таблицы.

Заметим, что ошибка прогноза e_i фактически является оценкой значений u_i. График ошибки e_i представлен на рис. 2.2. Следует отметить факт равенства нулю суммы e_i=0, что согласуется с первым ограничением модели парной регрессии - Eu_i=0, i=1,…,n. 



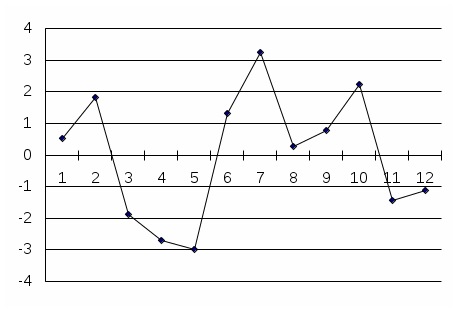
Рис. 2.2. График ошибки прогноза
В модели (2.2) функция f может быть и нелинейной. Причем выделяют два класса нелинейных регрессий:

• 
  регрессии, нелинейные относительно включенной объясняющей переменной, но линейные по параметрам, например полиномы разных степеней - Y_i =a₀ + a₁X_i + a₂X_i²+ u_i, i=1,…,n или гипербола - Y_i =a₀ + a₁/X_i + u_i, i=1,…,n;
  
• 
  регрессии нелинейные по оцениваемым параметрам, например степенная функция - Y_i =a₀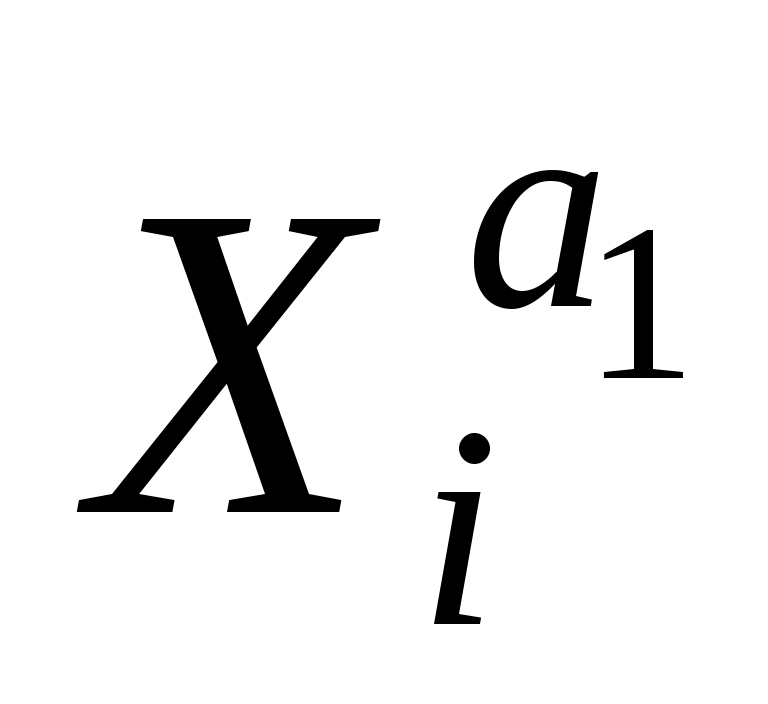 u_i, i=1,…,n, или показательная функция - Y_i = 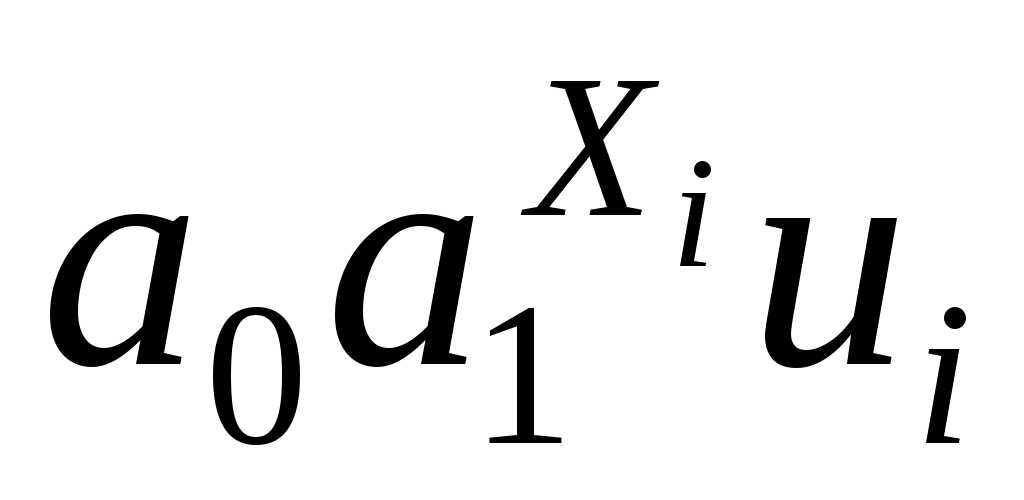, i=1,…,n.
  

В первом случае МНК применяется так же, как и в линейной регрессии, поскольку после замены, например, в квадратичной параболе Y_i =a₀ + a₁X_i + a₂X_i²+ u_i переменной X_i² на X_1i: X_i²=X_1i, получаем линейное уравнение регрессии Y_i =a₀ + a₁X_i + a₂

---

X_1i+ u_i, i=1,…,n.

Во втором случае в зависимости от вида функции возможно применение линеаризующих преобразований, приводящих функцию к виду линейной. Например, для степенной функции Y_i =a₀ u_iпосле логарифмирования получаем линейную функцию в логарифмах и применяем МНК.

Однако для, например, модели Y_i =a₀+a₂ +u_iлинеаризующее преобразование отсутствует, и приходится применять другие способы оценивания (например, нелинейный МНК).

---

2.4. Коэффициент корреляции, коэффициент детерминации, корреляционное отношение

Для трактовки линейной связи между двумя переменными акцентируют внимание на коэффициенте корреляции.

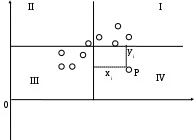
Пусть имеется выборка наблюдений (X_i, Y_i), i=1,...,n, которая представлена на диаграмме рассеяния, именуемой также полем корреляции (рис. 2.3).

Y

X
Рис. 2.3. Диаграмма рассеяния
Разобьем диаграмму на четыре квадранта так, что для любой точки P(X_i, Y_i) будут определены отклонения

Ясно, что для всех точек I квадранта x_iy_i>0; для всех точек II квадранта x_iy_i<0; для всех точек III квадранта x_iy_i>0; для всех точек IV квадранта x_iy_i<0. Следовательно, величина x_iy_i может служить мерой зависимости между переменными X и Y. Если большая часть точек лежит в первом и третьем квадрантах, то x_iy_i>0 и зависимость положительная, если большая часть точек лежит во втором и четвертом квадрантах, то x_iy_i<0 и зависимость отрицательная. Наконец, если точки рассеиваются по всем четырем квадрантам x_iy_i близка к нулю и между X и Y связи нет.

Указанная мера зависимости изменяется при выборе единиц измерения переменных X и Y. Выразив x_iy_i в единицах среднеквадратических отклонений, получим после усреднения выборочный коэффициент корреляции:

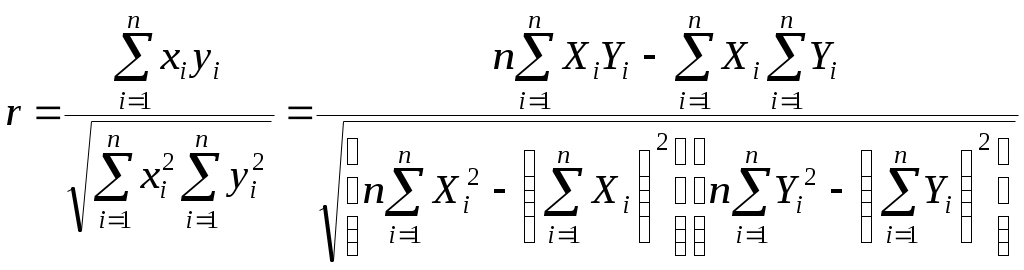(2.9)

Из последнего выражения можно после преобразований получить следующую формулу для квадрата коэффициента корреляции:

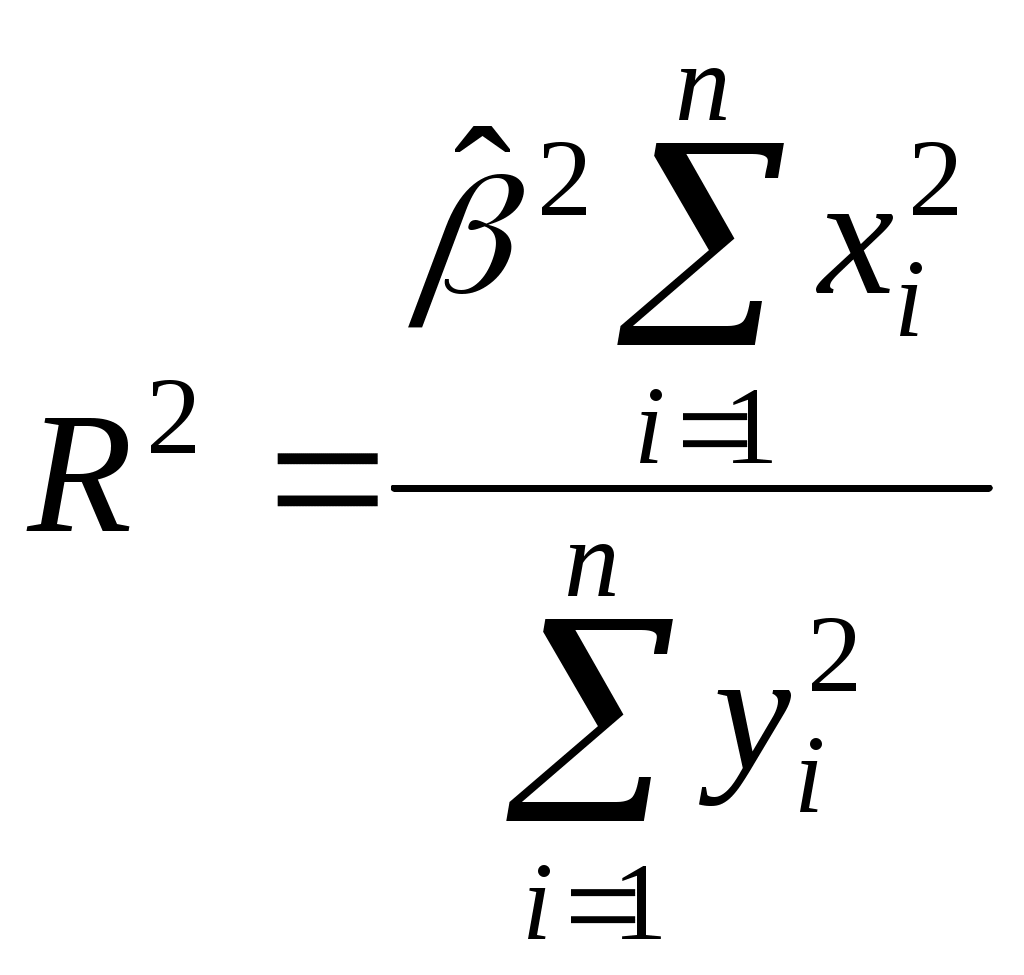или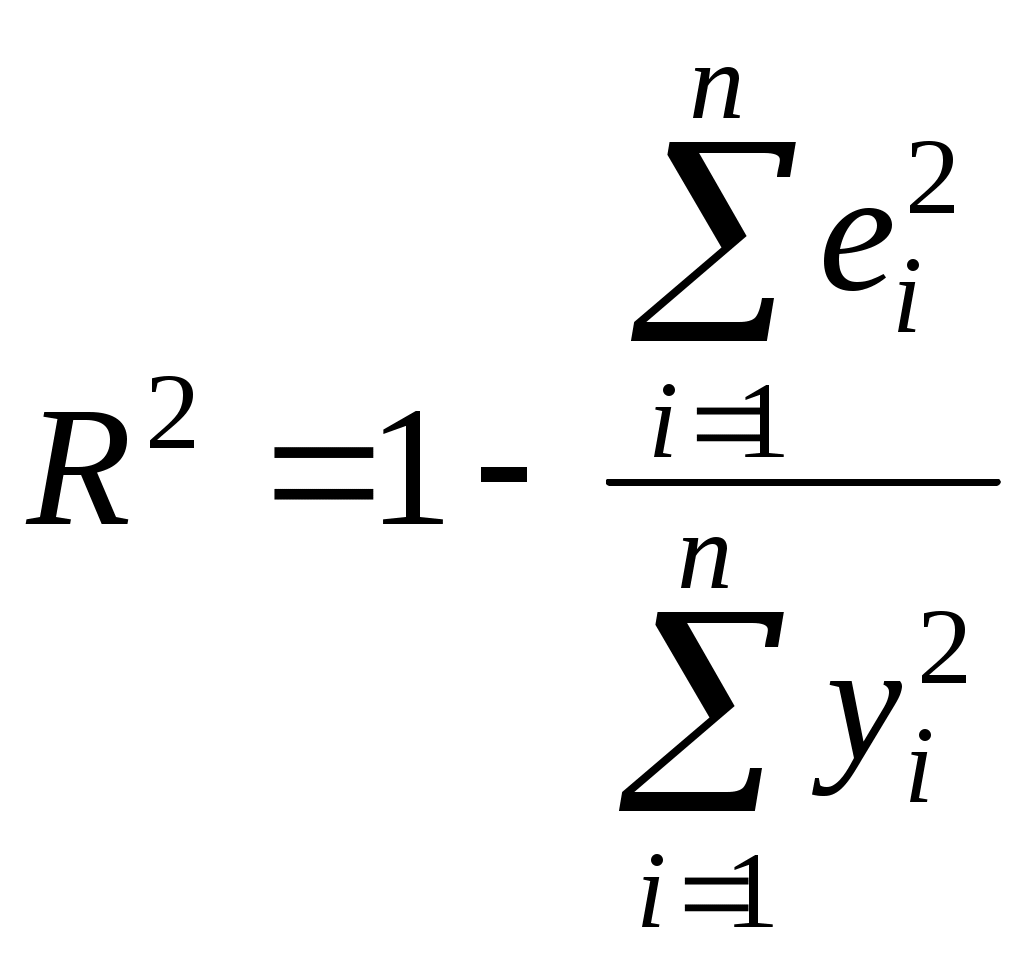

(2.10)

Квадрат коэффициента корреляции называется коэффициентом детерминации. Согласно (2.10) значение коэффициента детерминации не может быть больше единицы, причем это максимальное значение будет достигнуто при

---

=0, т.е. когда все точки диаграммы рассеяния лежат в точности на прямой. Следовательно, значения коэффициента корреляции лежат в числовом промежутке от -1 до +1.

Кроме того, из (2.10) следует, что коэффициент детерминации равен доле дисперсии Y (знаменатель формулы), объясненной линейной зависимостью от X (числитель формулы). Это обстоятельство позволяет использовать R² как обобщенную меру "качества" статистического подбора модели (2.6). Чем лучше регрессия соответствует наблюдениям, тем меньше и тем ближе R² к 1, и наоборот, чем "хуже" подгонка линии регрессии к данным, тем ближе значение R² к 0.

Поскольку коэффициент корреляции симметричен относительно X и Y, то есть r_XY=r_YX, то можно говорить о корреляции как о мере взаимозависимости переменных. Однако из того, что значения этого коэффициента близки по модулю к единице, нельзя сделать ни один из следующих выводов: Y является причиной X; X является причиной Y; X и Y совместно зависят от какой-то третьей переменной. Величина r ничего не говорит о причинно-следственных связях. Эти вопросы должны решаться, исходя из содержательного анализа задачи. Следует избегать и так называемых ложных корреляций, т.е. нельзя пытаться связать явления, между которыми отсутствуют реальные причинно-следственные связи. Например, корреляция между успехами местной футбольной команды и индексом Доу-Джонса. Классическим является пример ложной корреляции, приведенный в начале ХХ века известным российским статистиком А.А. Чупровым: если в качестве независимой переменной взять число пожарных команд в городе, а в качестве зависимой переменной – сумму убытков от пожаров за год, то между ними есть прямая корреляционная зависимость, т.е. чем больше пожарных команд, тем больше сумма убытков. На самом деле здесь нет причинно-следственной связи, а есть лишь следствия общей причины – величины города.

Проверка гипотезы о значимости выборочного коэффициента корреляции эквивалентна проверке гипотезы о =0 (см. ниже) и, следовательно, равносильна проверке основной гипотезы об отсутствии линейной связи между Y и X. Вычисляя значение t-статистики

---

,

вывод о значимости r делается при t>t_, где t_ - соответствующее табличное значение t-распределения с (n-2) степенями свободы и уровнем значимости .

Пример. Вычислим коэффициент корреляции и проверим его значимость для нашего примера табл. 2.1.

По (2.9) r=43145/(4651040068,25)^0,5=0,9994. R²=0,998. Значение t-статистики t=0,9994[10/(1-0,998)]^0,5=70,67. Поскольку t_0,05;10=2,228, то t>t_0,05;10 и коэффициент корреляции значим. Следовательно, можно считать, что линейная связь между переменными Y и X в примере существует. 

Если между переменными имеет место нелинейная зависимость, то коэффициент корреляции теряет смысл как характеристика степени тесноты связи. В этом случае используется наряду с расчетом коэффициента детерминации расчет корреляционного отношения.

Предположим, что выборочные данные могут быть сгруппированы по оси объясняющей переменной X. Обозначим s – число интервалов группирования, (j=1,…,s) – число выборочных точек, попавших в j-й интервал группирования, - среднее значение ординат точек, попавших в j-й интервал группирования, - общее среднее по выборке. С учетом формул для оценок выборочных дисперсий среднего значения Y внутри интервалов группирования и суммарной дисперсии результатов наблюдения получим:

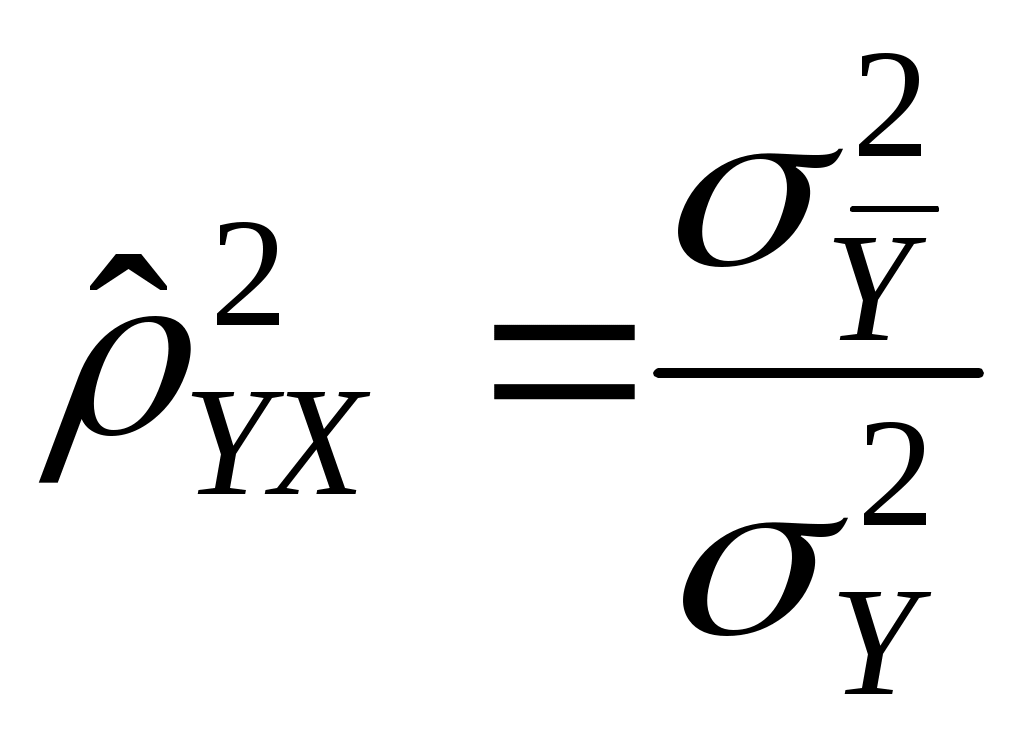. (2.11)

Величину в (2.11) называют корреляционным отношением зависимой переменной Y по независимой переменной X. Его вычисление не предполагает каких-либо допущений о виде функции регрессии.

Величина по определению неотрицательная и не превышает единицы, причем

---