Файл: 1 Бейсызыты буындарды типтері жне оларды сипаттамалары.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 173
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
аралығымен қиылыспайтын, немесе нақты осьте 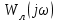 сипаттамасы
сипаттамасы 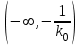 аралығымен қиып өтпейтін жағдайды қарастырайық. Тұйықталған жүйе орнықты болуы үшін Найквист критерийіне сәйкес бұл шарт жеткілікті. Себебі
аралығымен қиып өтпейтін жағдайды қарастырайық. Тұйықталған жүйе орнықты болуы үшін Найквист критерийіне сәйкес бұл шарт жеткілікті. Себебі 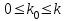 болғандықтан
болғандықтан класына жататын барлық сызықты жүйелердің орнықтылық шарты болып
класына жататын барлық сызықты жүйелердің орнықтылық шарты болып 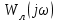 нақты осьтің
нақты осьтің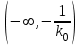 аралығымен қиылысыпайтын шарты болып табылады.
аралығымен қиылысыпайтын шарты болып табылады.
 класына жататын F(x) кез келген сызықты емес функциясының абсолютті орнықтылықтың жеткілікті шартын В.М.Попов көрсеткен. Бұл шартты дәлелсіз келтіреміз. Орнықты сызықты бөлігі бар сызықты емес жүйенің тепе-теңдік жағдайы орнықты болуы үшін келесі шарттардың орындалуы жеткілікті.
класына жататын F(x) кез келген сызықты емес функциясының абсолютті орнықтылықтың жеткілікті шартын В.М.Попов көрсеткен. Бұл шартты дәлелсіз келтіреміз. Орнықты сызықты бөлігі бар сызықты емес жүйенің тепе-теңдік жағдайы орнықты болуы үшін келесі шарттардың орындалуы жеткілікті.
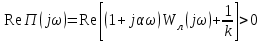 (4.2)
(4.2)
Критерийді тәжірибеде пайдалану үшін оның геометриялық мағынасын қолданған жөн. Бұл үшін алдын-ала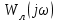 -мен төмендегідей байланысты сызықты бөлігінің түрі өзгертілген жиілік сипаттамасын
-мен төмендегідей байланысты сызықты бөлігінің түрі өзгертілген жиілік сипаттамасын 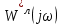 енгіземіз.
енгіземіз.
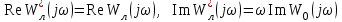 (4.3)
(4.3)
Түрі өзгертілген сипаттаманың ерекшеліктері: оның нақты бөлігі бастапқы сипаттаманың нақты бөлігіне тең, жорамал бөлігі бастапқы сипаттаманың жорамал бөлігін ω көбейткенге тең (4.2-сурет).
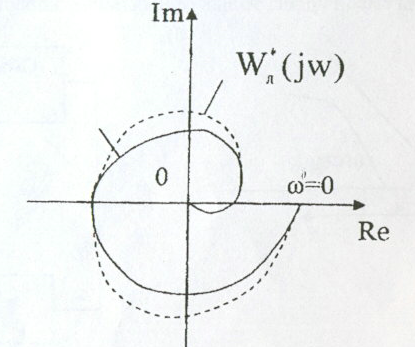
4.2-сурет. Түрі өзгертілген сипаттама
34. В.М. Поповтың әдісінің геометриялық мағынасы
Енді Попов критерийінің (4.2)-нің негізінде геометриялық түсініктемесіне тоқталайық.
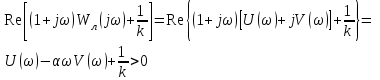 немесе (4.4)
немесе (4.4)
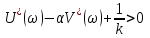
барлық үшін. Бұл теңсіздік Попов критерийінің басқа түрін көрсетеді.
үшін. Бұл теңсіздік Попов критерийінің басқа түрін көрсетеді.
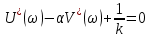 (4.5)
(4.5)
шарты орындалғанда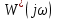 түзудің теңдеуін аламыз. Ал түзу бұрыштық коэффициенті
түзудің теңдеуін аламыз. Ал түзу бұрыштық коэффициенті 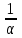 -ге тең, координаты
-ге тең, координаты 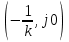 болатындай нүктеден өтеді.
болатындай нүктеден өтеді.
Осыдан Попов критерийнің графикалық интерпретациясы шығады: сызықты емес жүйенің орнықтылығын орнату үшін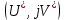 жазықтығында
жазықтығында 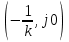 нүктесінен өтетін барлық
нүктесінен өтетін барлық 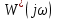 қажетті қисықтар оң жағында орналасатын түзуді таңдау жеткілікті.
қажетті қисықтар оң жағында орналасатын түзуді таңдау жеткілікті.
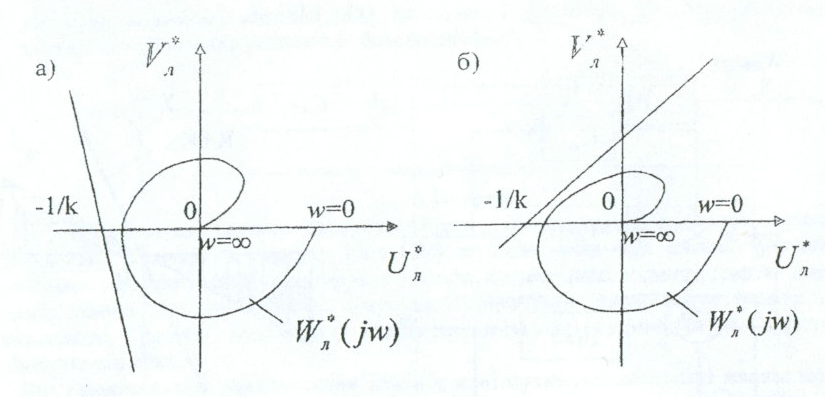
4.3-сурет. Попов критерийінің графикалық түсіндірмесі
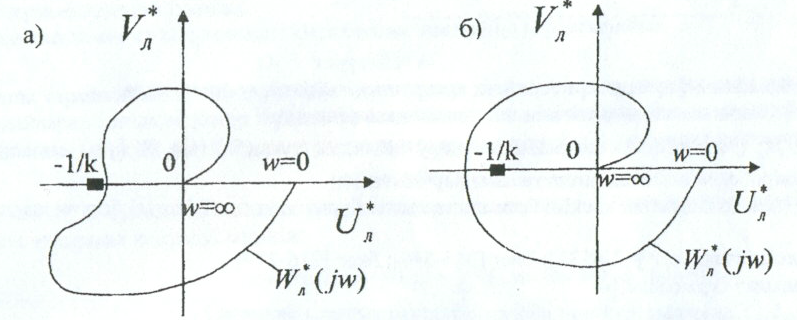
4.4-сурет. Попов критерийінің орындалу жағдайлары
(4.3а,б-)суретінде Попов критерийінің орындалу жағдайлары, ал (4.4,а,б)-суретінде критерийдің орныдалмау жағдайлары көрсетілген.
(4.4,а) суретінде бұрышында y=F(x) бірмәнді сызықсыз сипаттамасының орнықтылық шартының жеткіліктілігі осы бұрыштағы сызықты сипаттаманың орнықтылық шартының жеткіліктілігі осы бұрыштағы
бұрышында y=F(x) бірмәнді сызықсыз сипаттамасының орнықтылық шартының жеткіліктілігі осы бұрыштағы сызықты сипаттаманың орнықтылық шартының жеткіліктілігі осы бұрыштағы 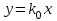 сызықты сипаттаманың орнықтылық шартының қажеттілігі мен жеткіліктілігінен қатаңырақ екені көрсетілген.
сызықты сипаттаманың орнықтылық шартының қажеттілігі мен жеткіліктілігінен қатаңырақ екені көрсетілген.
35. В.М. Попов критерийін орнықсыз сызықты бөлігі бар жүйенің орнықтылығын зерттеуге қолдану
В.М.Попов критерийі орнықсыз сызықты бөлігі бар жүйелерде де қолданылады.
Егер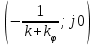 нүктесінен сипаттамасының сол жағынан өтетін түзу сызықты жүргізуге болса, онда жүйе абсолютті орнықты.
нүктесінен сипаттамасының сол жағынан өтетін түзу сызықты жүргізуге болса, онда жүйе абсолютті орнықты.
Мұнда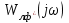 берілген
берілген 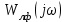 сипаттаманың түрі өзгертілген сипаттамасы болып табылады . .
сипаттаманың түрі өзгертілген сипаттамасы болып табылады . .
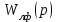 беріліс функциясы бастапқы беріліс функциясымен келесі қатынаспен байланысты:
беріліс функциясы бастапқы беріліс функциясымен келесі қатынаспен байланысты:
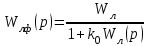
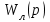 мұнда жүйенің сызықты бөлігінің беріліс функциясы;
мұнда жүйенің сызықты бөлігінің беріліс функциясы; 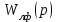 -
- 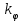 беріліс коэффициентінің шамасын дұрыс таңдау арқасында орнықты болатын
беріліс коэффициентінің шамасын дұрыс таңдау арқасында орнықты болатын 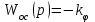 қосымша кері байланысы бар жүйенің сызықты бөлігінің беріліс функциясы.
қосымша кері байланысы бар жүйенің сызықты бөлігінің беріліс функциясы.
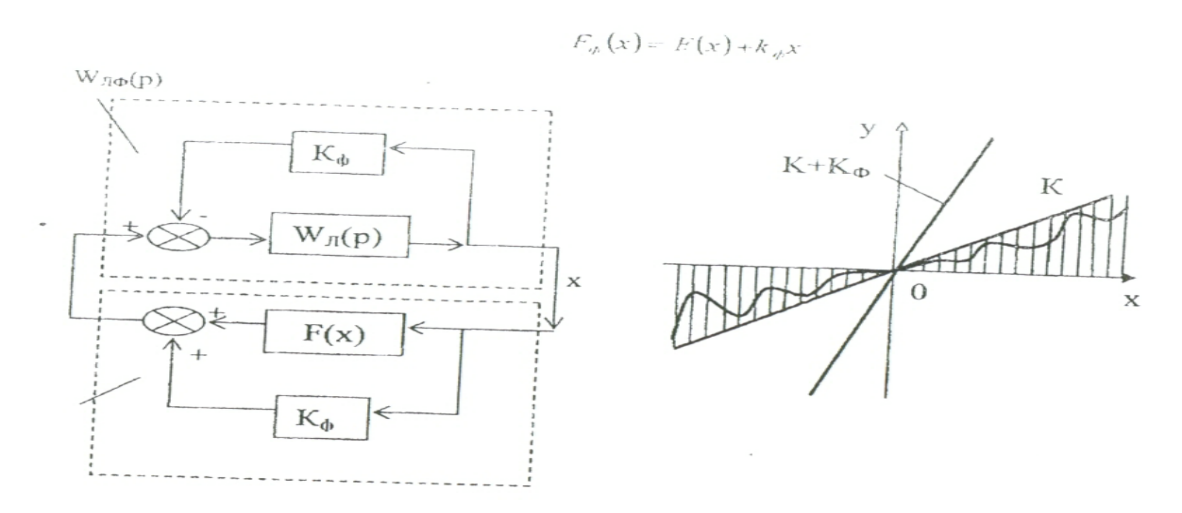
4.5-сурет. Попов критерийінің қолданылуы
Графикалық формада критерийдің артықшылығы оның қолдану мүмкіндігінде:
а) кез келген күрделі сызықты бөлігі бар жүйеде;
б) сипаттамасының тек қана тәжірибеден алынған сызықты бөлігі бар болғанда, оны
сипаттамасының тек қана тәжірибеден алынған сызықты бөлігі бар болғанда, оны 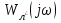 айналдыру қиындық туғызбайтын жағдайда;
айналдыру қиындық туғызбайтын жағдайда;
в) бейсызықтылықтың кескіні болмағанда, тек оның қандай бұрышта жататындығы белгілі болған жағдайда.
36. Орнықтылық пен автотербелісті зерттеудің жуықтау әдістері.
Гармоникалық сызықтау әдісі –автотербелістерді зерттейтін әдіс. Ол автотербелістің бар болу шарттарын және автотербелістердің сызықсыз жүйелерінің мүмкін параметрлерін анықтауға мүмкіндік береді.
Гармоникалық сызықтау әдісінің негізін 1934 жылы Н.М.Крылов және Н.И.Боголюбов қалаған. Автоматты басқару теориясының есептеріне қолданылу үшін әдіс Е.П.Попов пен Л.С.Гольдфарбпен жалғасын тапты. Оның басқа атаулары-гармоникалық баланс әдісі, функцияларды бейнелеуші әдіс. Сызықты жүйе тізбектей қосылған сызықсыз элемент БЭ пен сызықты бөліктен СБ (5.1-сурет) тұрсын және периодты тербелістер режимінде болсын делік.

5.1-сурет. Тізбектей қосылған сызықсыз жүйе
БЭ шығысында сигнал периодты, бірақ гармоникалық емес және гармоникалық құраушылар спектрінен тұрады. Бірақ СБ жүйеден өтіп бұл сигнал сүзгіден өтеді. Бұл тұжырым гармоникалық сызықтау әдісін қолданудың қажетті шарты және де оны сүзгі гипотезасы деп атайды. Көптеген тәжірибелік жағдайларда сүзгі гипотезасы орындалады, себебі амплитуда бойынша жоғарғы гармоникалық, әдетте, бірінші гармоникадан өтеді.
Бұл гармоникалық сызықтау әдісінің мәні сызықсыз элементті жалпы жағдайда БЭ кірісіндегі гармоникалық сигналдың амплитудасы мен жиілігіне тәуелді тұрақты емес беріліс коэффициенті бар эквивалентті сызықты буынмен алмастыру. Орнықты периодты режимдерді қарастырғанда автотербелістерді зерттеуде сызықты АБЖ анализінің белгілі әдістерін қолдануға болады.
Сызықсыз элемент инерционды емес болған жағдайды қарастырайық.
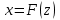 (5.1)
(5.1)
Жалпы гармоникалық сызықтау әдісі бұдан да қиын динамикалық сызықсыздығы бар жағдайларда, сонымен қатар жүйеде бірнеше сызықсыздық болған кезінде де қолданылады.
Кіріс сигналы жоқ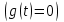 және сызықсыз элемент кірісінде гармоникалық әсер болсын.
және сызықсыз элемент кірісінде гармоникалық әсер болсын.
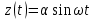 (5.2)
(5.2)
Бұл жағдайда сызықсыз элементтің шығыс сигналы периодты, бірақ синусоидалды емес және Фурье қатарына жіктелуі мүмкін.
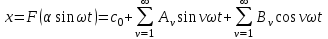 (5.3)
(5.3)
Мұндағы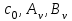 келесі формулалармен анықталған Фурье қатарының коэффициенттері
келесі формулалармен анықталған Фурье қатарының коэффициенттері
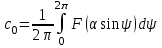 (5.4)
(5.4)
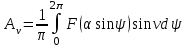 (5.5)
(5.5)
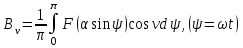 (5.6)
(5.6)
Практикалық есептеулерде бұл формулалар қолданылмайды, типтік бейсызықдыққа дайын қатынастар бар.
37.Бейсызықтылықты гармоникалық сызықтау
Гармоникалық сызықтау әдісі –автотербелістерді зерттейтін әдіс. Ол автотербелістің бар болу шарттарын және автотербелістердің сызықсыз жүйелерінің мүмкін параметрлерін анықтауға мүмкіндік береді.
Гармоникалық сызықтау әдісінің негізін 1934 жылы Н.М.Крылов және Н.И.Боголюбов қалаған. Автоматты басқару теориясының есептеріне қолданылу үшін әдіс Е.П.Попов пен Л.С.Гольдфарбпен жалғасын тапты. Оның басқа атаулары-гармоникалық баланс әдісі, функцияларды бейнелеуші әдіс. Сызықты жүйе тізбектей қосылған сызықсыз элемент БЭ пен сызықты бөліктен СБ (5.1-сурет) тұрсын және периодты тербелістер режимінде болсын делік.

Бұл бейсызықтықты статикалық сипаттама тақ-симметриялы функция болғанда орындалады (5.2-сурет).

5.2-сурет. Бейсызықты статикалық сипаттама
Гармоникалық сызықтау кезінде БЭ шығыс сигналы өзінің бірінші гармоникасын көрсетеді:
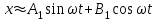 (5.7)
(5.7)
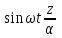 (5.8)
(5.8)
және (5.2) дифференциалданғаннан кейін уақыт бойынша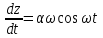
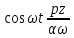 (5.9)
(5.9)
(5.7)-ге (5.8) және (5.9)-ды қойып алатынымыз: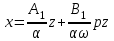
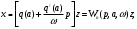
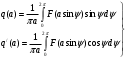 (5.10)
(5.10)
(5.10) қатынасы БЭ-ң кіріс және шығыс шамаларын сызықты байланыстырады және бейсызықтылықтың гармоникалық сызықтау формуласы деп аталады.
Гармоникалық сызықтаудың қарапайым сызықтаудан айырмашылығы q(a) және q/ (a) коэффициенттері бейсызықтылықтың кірісіндегі гармоникалық тербеліс амплитудасына тәуелді.
Ашық АБЖ-ның беріліс функциясын былай анықтайды:
Сызықтанған жүйені зерттеу үшін сызықты теория әдісін қолдануға болады.
38. Импульстік жүйені үздіксіз түзету
Сигналдардың түрлендіру тәсіліне байланысты АБЖ үздіксіз және дискретті болып бөлінеді.
Үздіксіз жүйеде сигналдар үзілмейді.
Дискретті жүйеде үздіксіз сигналдарды үзетін элемент және Оларды дискреттіге түрлендіреді.
Үздіксіз сигналдардың дискретті сигналдарға түрлену процесі кванттау деп аталады.
Сигналдардың кванттауының үш әдісі бар:
а) деңгейі бойынша;
б) уақыт бойынша;
в) аралас деңгейі және уақыт бойынша.
Кванттау типіне байланысты дискретті жүйелер релелік (деңгейі бойынша кванттау), импульстік(уақыт бойынша) және цифрлік (аралас) болып бөлінеді. Дискретті АБЖ кең қолданыс тапты, Олар жоғары дәлдікпен және аналогты берілгендердің сандық көрсетілуі есебінен бөгеуілден қорғаушылықпен сипаттаталады. Берілген бөлімде тек импульстік жүйені қарастырамыз. Көптеген тұйықталған АБЖ-ні 7.1-суреттегідей көрсетуге болады.
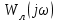 сипаттамасы
сипаттамасы 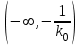 аралығымен қиып өтпейтін жағдайды қарастырайық. Тұйықталған жүйе орнықты болуы үшін Найквист критерийіне сәйкес бұл шарт жеткілікті. Себебі
аралығымен қиып өтпейтін жағдайды қарастырайық. Тұйықталған жүйе орнықты болуы үшін Найквист критерийіне сәйкес бұл шарт жеткілікті. Себебі 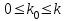 болғандықтан
болғандықтан класына жататын барлық сызықты жүйелердің орнықтылық шарты болып
класына жататын барлық сызықты жүйелердің орнықтылық шарты болып 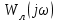 нақты осьтің
нақты осьтің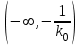 аралығымен қиылысыпайтын шарты болып табылады.
аралығымен қиылысыпайтын шарты болып табылады. класына жататын F(x) кез келген сызықты емес функциясының абсолютті орнықтылықтың жеткілікті шартын В.М.Попов көрсеткен. Бұл шартты дәлелсіз келтіреміз. Орнықты сызықты бөлігі бар сызықты емес жүйенің тепе-теңдік жағдайы орнықты болуы үшін келесі шарттардың орындалуы жеткілікті.
класына жататын F(x) кез келген сызықты емес функциясының абсолютті орнықтылықтың жеткілікті шартын В.М.Попов көрсеткен. Бұл шартты дәлелсіз келтіреміз. Орнықты сызықты бөлігі бар сызықты емес жүйенің тепе-теңдік жағдайы орнықты болуы үшін келесі шарттардың орындалуы жеткілікті.-
Барлық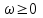 үшін Поповтың
үшін Поповтың 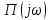 функциясының нақты бөлігі оң болатындай a нақты саны табылады.
функциясының нақты бөлігі оң болатындай a нақты саны табылады.
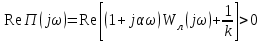 (4.2)
(4.2)-
F(x)функциясы класына жатады.
класына жатады.
Критерийді тәжірибеде пайдалану үшін оның геометриялық мағынасын қолданған жөн. Бұл үшін алдын-ала
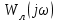 -мен төмендегідей байланысты сызықты бөлігінің түрі өзгертілген жиілік сипаттамасын
-мен төмендегідей байланысты сызықты бөлігінің түрі өзгертілген жиілік сипаттамасын 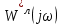 енгіземіз.
енгіземіз.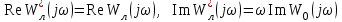 (4.3)
(4.3)Түрі өзгертілген сипаттаманың ерекшеліктері: оның нақты бөлігі бастапқы сипаттаманың нақты бөлігіне тең, жорамал бөлігі бастапқы сипаттаманың жорамал бөлігін ω көбейткенге тең (4.2-сурет).

4.2-сурет. Түрі өзгертілген сипаттама
34. В.М. Поповтың әдісінің геометриялық мағынасы
Енді Попов критерийінің (4.2)-нің негізінде геометриялық түсініктемесіне тоқталайық.
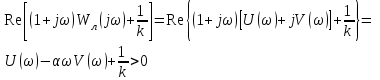 немесе (4.4)
немесе (4.4)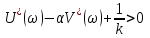
барлық
 үшін. Бұл теңсіздік Попов критерийінің басқа түрін көрсетеді.
үшін. Бұл теңсіздік Попов критерийінің басқа түрін көрсетеді.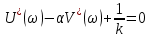 (4.5)
(4.5)шарты орындалғанда
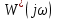 түзудің теңдеуін аламыз. Ал түзу бұрыштық коэффициенті
түзудің теңдеуін аламыз. Ал түзу бұрыштық коэффициенті 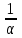 -ге тең, координаты
-ге тең, координаты 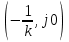 болатындай нүктеден өтеді.
болатындай нүктеден өтеді. Осыдан Попов критерийнің графикалық интерпретациясы шығады: сызықты емес жүйенің орнықтылығын орнату үшін
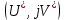 жазықтығында
жазықтығында 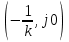 нүктесінен өтетін барлық
нүктесінен өтетін барлық 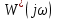 қажетті қисықтар оң жағында орналасатын түзуді таңдау жеткілікті.
қажетті қисықтар оң жағында орналасатын түзуді таңдау жеткілікті. 
4.3-сурет. Попов критерийінің графикалық түсіндірмесі

4.4-сурет. Попов критерийінің орындалу жағдайлары
(4.3а,б-)суретінде Попов критерийінің орындалу жағдайлары, ал (4.4,а,б)-суретінде критерийдің орныдалмау жағдайлары көрсетілген.
(4.4,а) суретінде
 бұрышында y=F(x) бірмәнді сызықсыз сипаттамасының орнықтылық шартының жеткіліктілігі осы бұрыштағы сызықты сипаттаманың орнықтылық шартының жеткіліктілігі осы бұрыштағы
бұрышында y=F(x) бірмәнді сызықсыз сипаттамасының орнықтылық шартының жеткіліктілігі осы бұрыштағы сызықты сипаттаманың орнықтылық шартының жеткіліктілігі осы бұрыштағы 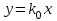 сызықты сипаттаманың орнықтылық шартының қажеттілігі мен жеткіліктілігінен қатаңырақ екені көрсетілген.
сызықты сипаттаманың орнықтылық шартының қажеттілігі мен жеткіліктілігінен қатаңырақ екені көрсетілген.35. В.М. Попов критерийін орнықсыз сызықты бөлігі бар жүйенің орнықтылығын зерттеуге қолдану
В.М.Попов критерийі орнықсыз сызықты бөлігі бар жүйелерде де қолданылады.
Егер
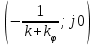 нүктесінен сипаттамасының сол жағынан өтетін түзу сызықты жүргізуге болса, онда жүйе абсолютті орнықты.
нүктесінен сипаттамасының сол жағынан өтетін түзу сызықты жүргізуге болса, онда жүйе абсолютті орнықты.
Мұнда
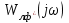 берілген
берілген 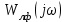 сипаттаманың түрі өзгертілген сипаттамасы болып табылады . .
сипаттаманың түрі өзгертілген сипаттамасы болып табылады . . 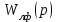 беріліс функциясы бастапқы беріліс функциясымен келесі қатынаспен байланысты:
беріліс функциясы бастапқы беріліс функциясымен келесі қатынаспен байланысты: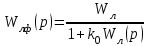
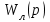 мұнда жүйенің сызықты бөлігінің беріліс функциясы;
мұнда жүйенің сызықты бөлігінің беріліс функциясы; 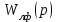 -
- 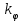 беріліс коэффициентінің шамасын дұрыс таңдау арқасында орнықты болатын
беріліс коэффициентінің шамасын дұрыс таңдау арқасында орнықты болатын 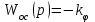 қосымша кері байланысы бар жүйенің сызықты бөлігінің беріліс функциясы.
қосымша кері байланысы бар жүйенің сызықты бөлігінің беріліс функциясы.
4.5-сурет. Попов критерийінің қолданылуы
Графикалық формада критерийдің артықшылығы оның қолдану мүмкіндігінде:
а) кез келген күрделі сызықты бөлігі бар жүйеде;
б)
 сипаттамасының тек қана тәжірибеден алынған сызықты бөлігі бар болғанда, оны
сипаттамасының тек қана тәжірибеден алынған сызықты бөлігі бар болғанда, оны 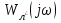 айналдыру қиындық туғызбайтын жағдайда;
айналдыру қиындық туғызбайтын жағдайда;в) бейсызықтылықтың кескіні болмағанда, тек оның қандай бұрышта жататындығы белгілі болған жағдайда.
36. Орнықтылық пен автотербелісті зерттеудің жуықтау әдістері.
Гармоникалық сызықтау әдісі –автотербелістерді зерттейтін әдіс. Ол автотербелістің бар болу шарттарын және автотербелістердің сызықсыз жүйелерінің мүмкін параметрлерін анықтауға мүмкіндік береді.
Гармоникалық сызықтау әдісінің негізін 1934 жылы Н.М.Крылов және Н.И.Боголюбов қалаған. Автоматты басқару теориясының есептеріне қолданылу үшін әдіс Е.П.Попов пен Л.С.Гольдфарбпен жалғасын тапты. Оның басқа атаулары-гармоникалық баланс әдісі, функцияларды бейнелеуші әдіс. Сызықты жүйе тізбектей қосылған сызықсыз элемент БЭ пен сызықты бөліктен СБ (5.1-сурет) тұрсын және периодты тербелістер режимінде болсын делік.

5.1-сурет. Тізбектей қосылған сызықсыз жүйе
БЭ шығысында сигнал периодты, бірақ гармоникалық емес және гармоникалық құраушылар спектрінен тұрады. Бірақ СБ жүйеден өтіп бұл сигнал сүзгіден өтеді. Бұл тұжырым гармоникалық сызықтау әдісін қолданудың қажетті шарты және де оны сүзгі гипотезасы деп атайды. Көптеген тәжірибелік жағдайларда сүзгі гипотезасы орындалады, себебі амплитуда бойынша жоғарғы гармоникалық, әдетте, бірінші гармоникадан өтеді.
Бұл гармоникалық сызықтау әдісінің мәні сызықсыз элементті жалпы жағдайда БЭ кірісіндегі гармоникалық сигналдың амплитудасы мен жиілігіне тәуелді тұрақты емес беріліс коэффициенті бар эквивалентті сызықты буынмен алмастыру. Орнықты периодты режимдерді қарастырғанда автотербелістерді зерттеуде сызықты АБЖ анализінің белгілі әдістерін қолдануға болады.
Сызықсыз элемент инерционды емес болған жағдайды қарастырайық.
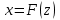 (5.1)
(5.1) Жалпы гармоникалық сызықтау әдісі бұдан да қиын динамикалық сызықсыздығы бар жағдайларда, сонымен қатар жүйеде бірнеше сызықсыздық болған кезінде де қолданылады.
Кіріс сигналы жоқ
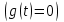 және сызықсыз элемент кірісінде гармоникалық әсер болсын.
және сызықсыз элемент кірісінде гармоникалық әсер болсын.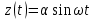 (5.2)
(5.2)Бұл жағдайда сызықсыз элементтің шығыс сигналы периодты, бірақ синусоидалды емес және Фурье қатарына жіктелуі мүмкін.
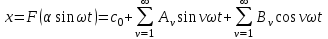 (5.3)
(5.3)Мұндағы
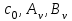 келесі формулалармен анықталған Фурье қатарының коэффициенттері
келесі формулалармен анықталған Фурье қатарының коэффициенттері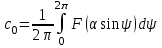 (5.4)
(5.4)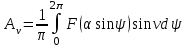 (5.5)
(5.5)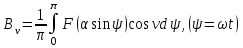 (5.6)
(5.6)Практикалық есептеулерде бұл формулалар қолданылмайды, типтік бейсызықдыққа дайын қатынастар бар.
37.Бейсызықтылықты гармоникалық сызықтау
Гармоникалық сызықтау әдісі –автотербелістерді зерттейтін әдіс. Ол автотербелістің бар болу шарттарын және автотербелістердің сызықсыз жүйелерінің мүмкін параметрлерін анықтауға мүмкіндік береді.
Гармоникалық сызықтау әдісінің негізін 1934 жылы Н.М.Крылов және Н.И.Боголюбов қалаған. Автоматты басқару теориясының есептеріне қолданылу үшін әдіс Е.П.Попов пен Л.С.Гольдфарбпен жалғасын тапты. Оның басқа атаулары-гармоникалық баланс әдісі, функцияларды бейнелеуші әдіс. Сызықты жүйе тізбектей қосылған сызықсыз элемент БЭ пен сызықты бөліктен СБ (5.1-сурет) тұрсын және периодты тербелістер режимінде болсын делік.

Бұл бейсызықтықты статикалық сипаттама тақ-симметриялы функция болғанда орындалады (5.2-сурет).

5.2-сурет. Бейсызықты статикалық сипаттама
Гармоникалық сызықтау кезінде БЭ шығыс сигналы өзінің бірінші гармоникасын көрсетеді:
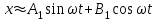 (5.7)
(5.7)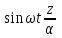 (5.8)
(5.8)және (5.2) дифференциалданғаннан кейін уақыт бойынша
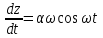
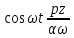 (5.9)
(5.9)(5.7)-ге (5.8) және (5.9)-ды қойып алатынымыз:
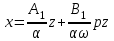
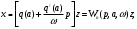
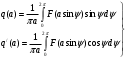 (5.10)
(5.10)(5.10) қатынасы БЭ-ң кіріс және шығыс шамаларын сызықты байланыстырады және бейсызықтылықтың гармоникалық сызықтау формуласы деп аталады.
Гармоникалық сызықтаудың қарапайым сызықтаудан айырмашылығы q(a) және q/ (a) коэффициенттері бейсызықтылықтың кірісіндегі гармоникалық тербеліс амплитудасына тәуелді.
Ашық АБЖ-ның беріліс функциясын былай анықтайды:
Сызықтанған жүйені зерттеу үшін сызықты теория әдісін қолдануға болады.
38. Импульстік жүйені үздіксіз түзету
Сигналдардың түрлендіру тәсіліне байланысты АБЖ үздіксіз және дискретті болып бөлінеді.
Үздіксіз жүйеде сигналдар үзілмейді.
Дискретті жүйеде үздіксіз сигналдарды үзетін элемент және Оларды дискреттіге түрлендіреді.
Үздіксіз сигналдардың дискретті сигналдарға түрлену процесі кванттау деп аталады.
Сигналдардың кванттауының үш әдісі бар:
а) деңгейі бойынша;
б) уақыт бойынша;
в) аралас деңгейі және уақыт бойынша.
Кванттау типіне байланысты дискретті жүйелер релелік (деңгейі бойынша кванттау), импульстік(уақыт бойынша) және цифрлік (аралас) болып бөлінеді. Дискретті АБЖ кең қолданыс тапты, Олар жоғары дәлдікпен және аналогты берілгендердің сандық көрсетілуі есебінен бөгеуілден қорғаушылықпен сипаттаталады. Берілген бөлімде тек импульстік жүйені қарастырамыз. Көптеген тұйықталған АБЖ-ні 7.1-суреттегідей көрсетуге болады.