Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Методы оптимальных решений.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 183
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
х5, у2, соответствующая разрешающей строке. Клетки следующей таблицы заполняются элементами, полученными в результате деления соответствующих элементов из предыдущей таблицы в нижних частях клеток на разрешающий элемент «10/3». Поскольку в нижних частях клеток таблицы все элементы положительные и разрешающий элемент также положительный, то в следующей таблице будет получено оптимальное решение и нет необходимости делить на две части клетки в последней таблице. Однако следует отметить, что в третьей строке в столбце bi есть нулевой элемент. Это свидетельствует о том, что двойственная задача имеет альтернативные решения:
Оптимальное решение ПЗЛП:
= (4, 4, 0, 0, 0, 0), 
= 144, оптимальное решение ДЗЛП: 
= (28/5, 4/5, 0, 0, 22/5),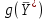 
= 144.
Данное решение аналогично решению, полученному в соответствии с методом одновременного решения пары взаимно двойственных задач для ПЗЛП и совпадает с решением ДЗЛП в отношении значения целевой функции. Однако поскольку ДЗЛП имеет альтернативные решения, то полученное в результате расчета решение является альтернативным по отношению к полученному первым методом.
Остальные этапы задания выполняются аналогично рассмотренным выше.
3.2.2. Обоснование оптимального плана перевозок
На четырех базах (пунктах отправления) A1, A2, A3, A4находится однородный груз в количествах, соответственно равных а1, а2, а3 и а4 единицам. Этот груз требуется перевести в три пункта назначения B1, B2, B3, B4соответственно в количествах b1, b2, b3 и b4. единиц. Стоимость перевозки единицы груза из i-го пункта отправления в j-й пункт назначения составляет cij денежных единиц. Определить оптимальный план перевозок, при котором общая стоимость перевозок будет минимальной.
Обязательные требования к решению задачи.
1. Проверить разрешимость транспортной задачи. Если задача не разрешима, свести ее к закрытой задаче введением фиктивного пункта отправления (поставщика) или пункта назначения (потребителя).
2. Построить экономико-математическую модель транспортной задачи.
3. Найти начальное решение транспортной задачи и проверить его на вырожденность.
4. Решить транспортную задачу методом потенциалов.
5. Решить транспортную задачу в среде Microsoft Exсel, приложить отчет.
Исходные данные варианта 0:
1. Проверка разрешимости транспортной задачи
Условие разрешимости транспортной задачи
Если сумма запасов груза равна суммарной потребности в нем: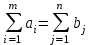
, то транспортная задача является закрытой.
Если сумма запасов не совпадает с суммой потребностей: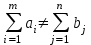
, то транспортная задача является открытой. При этом возможны два варианта:
а) если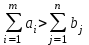
, то объем запасов превышает объем потребления, все потребители будут удовлетворены полностью и часть запасов останется не вывезенной. Для решения задачи вводят фиктивного (n + 1) потребителя, потребности которого 
.
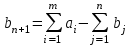б) если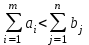
, то объем потребления превышает объем запасов, часть потребностей останется неудовлетворенной. Для решения такой задачи вводят фиктивного (m+ 1) поставщика, запас которого 
.
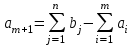Проверим условие разрешимости транспортной задачи: .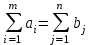
15 + 16 + 15 + 20 = 14 + 11 + 20 + 21; 66 = 66
Условие разрешимости транспортной задачи выполнено.
2. Экономико-математическая модель транспортной задачи.
Обозначим xij – количество груза, перевозимого из пункта Аi в пункт Bj:
Примечание. В правом верхнем углу каждой клетки приведены значения тарифа cij на перевозку единицы груза из i-го пункта отправления в j-й пункт назначения.
Математическая модель транспортной задачи имеет вид
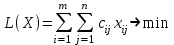
при ограничениях:
.
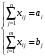
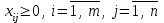Таким образом, целевая функция прямой транспортной задачи имеет вид
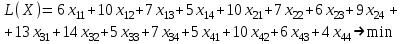
Ограничения транспортной задачи:
.
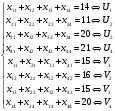
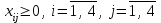Двойственная транспортная задача имеет вид:
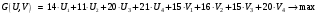
при ограничениях:
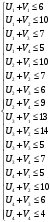
Где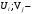
потенциалы, 
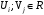, т.е. могут быть положительными, отрицательными или равными нулю.
3. Начальное решение транспортной задачи
Найдем исходное опорное решение по методу минимальной стоимости. Для этого заполним распределительную таблицу:
Метод минимальной стоимости нахождения начального решения транспортной задачи
В соответствии с методом минимальной стоимости грузы распределяются в первую очередь в те клетки, которым соответствует минимальный тариф перевозок сij. При этом объем поставки, вносимый в клетку, определяется как минимальное значение среди значений запаса и потребности: xij = min(ai, bj).
Далее поставки распределяются в незанятые клетки с наименьшими тарифами с учетом оставшихся запасов у поставщиков и удовлетворения спроса потребителей.
В случае нескольких клеток с одинаковыми значениями тарифов в первую очередь поставки распределяются в клетку с максимально возможной поставкой.
Процесс распределения продолжают до тех пор, пока все грузы от поставщиков не будут вывезены, а потребители не будут удовлетворены.
Минимальное значение имеет тариф перевозки от четвертого поставщика к четвертому потребителю с44 = 4, т.е. клетка (4, 4). В данную клетку вносится значение поставки, представляющее собой минимальное значение из значений запаса у четвертого поставщика и потребности у четвертого потребителя, т.е. min (21, 20) = 20. Это первая из искомых поставок х44 = 20.
Поскольку потребность четвертого поставщика поставкой х44 = 20 полностью удовлетворена, то потребность обнуляется, а в остальных клетках четвертого столбца проставляется прочерк – в эти клетки другое поставки вноситься не будут.
У четвертого поставщика остается еще одна единица груза (21 – 20 = 1), которая подлежит дальнейшему распределению:
| | yбаз | y2 | y1 | y6 |  |
| yсв | xсв xбаз | - x5 | - x4 | - x3 | bi |
| y5 | x2 | 1/5 | 3/5 | 3/5 | 4 |
| y4 | x1 | 3/10 | 2/5 | 1/10 | 4 |
| y3 | x6 | 1/5 | 8/5 | 12/5 | 0 |
| cj |  | 4/5 | 28/5 | 22/5 | 144 |
Оптимальное решение ПЗЛП:
= (4, 4, 0, 0, 0, 0), = 144, оптимальное решение ДЗЛП: = (28/5, 4/5, 0, 0, 22/5), 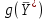= 144.
Данное решение аналогично решению, полученному в соответствии с методом одновременного решения пары взаимно двойственных задач для ПЗЛП и совпадает с решением ДЗЛП в отношении значения целевой функции. Однако поскольку ДЗЛП имеет альтернативные решения, то полученное в результате расчета решение является альтернативным по отношению к полученному первым методом.
Остальные этапы задания выполняются аналогично рассмотренным выше.
3.2.2. Обоснование оптимального плана перевозок
На четырех базах (пунктах отправления) A1, A2, A3, A4находится однородный груз в количествах, соответственно равных а1, а2, а3 и а4 единицам. Этот груз требуется перевести в три пункта назначения B1, B2, B3, B4соответственно в количествах b1, b2, b3 и b4. единиц. Стоимость перевозки единицы груза из i-го пункта отправления в j-й пункт назначения составляет cij денежных единиц. Определить оптимальный план перевозок, при котором общая стоимость перевозок будет минимальной.
Обязательные требования к решению задачи.
1. Проверить разрешимость транспортной задачи. Если задача не разрешима, свести ее к закрытой задаче введением фиктивного пункта отправления (поставщика) или пункта назначения (потребителя).
2. Построить экономико-математическую модель транспортной задачи.
3. Найти начальное решение транспортной задачи и проверить его на вырожденность.
4. Решить транспортную задачу методом потенциалов.
5. Решить транспортную задачу в среде Microsoft Exсel, приложить отчет.
Исходные данные варианта 0:
| Стоимость перевозки | В1 | В2 | В3 | В4 | Запасы |
| А1 | с11 = 6 | с12 = 10 | с13 = 7 | с14 = 5 | а1 = 14 |
| А2 | с21 = 10 | с22 = 7 | с23 = 6 | с24 = 9 | а2 = 11 |
| А3 | с31 = 13 | с32 = 14 | с33 = 5 | с34 = 7 | а3 = 20 |
| А4 | с41 = 5 | с42 = 10 | с43 = 6 | с44 = 4 | а4 = 21 |
| Потребности | b1 = 15 | b2 = 16 | b3 = 15 | b4 = 20 | - |
1. Проверка разрешимости транспортной задачи
Условие разрешимости транспортной задачи
Если сумма запасов груза равна суммарной потребности в нем:
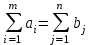, то транспортная задача является закрытой.Если сумма запасов не совпадает с суммой потребностей:
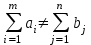, то транспортная задача является открытой. При этом возможны два варианта:а) если
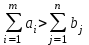, то объем запасов превышает объем потребления, все потребители будут удовлетворены полностью и часть запасов останется не вывезенной. Для решения задачи вводят фиктивного (n + 1) потребителя, потребности которого 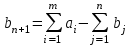.б) если
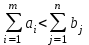, то объем потребления превышает объем запасов, часть потребностей останется неудовлетворенной. Для решения такой задачи вводят фиктивного (m+ 1) поставщика, запас которого 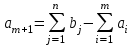.Проверим условие разрешимости транспортной задачи:
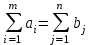.15 + 16 + 15 + 20 = 14 + 11 + 20 + 21; 66 = 66
Условие разрешимости транспортной задачи выполнено.
2. Экономико-математическая модель транспортной задачи.
Обозначим xij – количество груза, перевозимого из пункта Аi в пункт Bj:
| Объем перевозок | В1 | В2 | В3 | В4 | Запасы |
| А1 | 6 х11 | 10 х12 | 7 х13 | 5 х14 | а1 = 14 |
| А2 | 10 х21 | 7 х22 | 6 х23 | 9 х24 | а2 = 11 |
| А3 | 13 х31 | 14 х32 | 5 х33 | 7 х34 | а3 = 20 |
| А4 | 5 х41 | 10 х42 | 6 х43 | 4 х44 | а4 = 21 |
| Потребности | b1 = 15 | b2 = 16 | b3 = 15 | b4 = 20 | - |
Примечание. В правом верхнем углу каждой клетки приведены значения тарифа cij на перевозку единицы груза из i-го пункта отправления в j-й пункт назначения.
Математическая модель транспортной задачи имеет вид
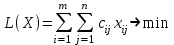
при ограничениях:
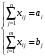
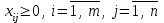.Таким образом, целевая функция прямой транспортной задачи имеет вид
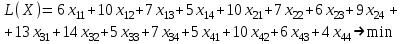
Ограничения транспортной задачи:
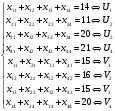
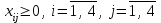.Двойственная транспортная задача имеет вид:
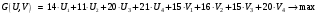
при ограничениях:
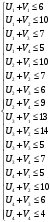
Где
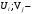потенциалы, 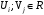, т.е. могут быть положительными, отрицательными или равными нулю.3. Начальное решение транспортной задачи
Найдем исходное опорное решение по методу минимальной стоимости. Для этого заполним распределительную таблицу:
| bj ai | 1 | 2 | 3 | 4 | |
| 15/ | 16/ | 15/ | 20/ | ||
| 1 | 14/ | 6 | 10 | 7 | 5 - |
| 2 | 11/ | 10 | 7 | 6 | 9 - |
| 3 | 20/ | 13 | 14 | 5 | 7 - |
| 4 | 21/ | 5 | 10 | 6 | 4 |
Метод минимальной стоимости нахождения начального решения транспортной задачи
В соответствии с методом минимальной стоимости грузы распределяются в первую очередь в те клетки, которым соответствует минимальный тариф перевозок сij. При этом объем поставки, вносимый в клетку, определяется как минимальное значение среди значений запаса и потребности: xij = min(ai, bj).
Далее поставки распределяются в незанятые клетки с наименьшими тарифами с учетом оставшихся запасов у поставщиков и удовлетворения спроса потребителей.
В случае нескольких клеток с одинаковыми значениями тарифов в первую очередь поставки распределяются в клетку с максимально возможной поставкой.
Процесс распределения продолжают до тех пор, пока все грузы от поставщиков не будут вывезены, а потребители не будут удовлетворены.
Минимальное значение имеет тариф перевозки от четвертого поставщика к четвертому потребителю с44 = 4, т.е. клетка (4, 4). В данную клетку вносится значение поставки, представляющее собой минимальное значение из значений запаса у четвертого поставщика и потребности у четвертого потребителя, т.е. min (21, 20) = 20. Это первая из искомых поставок х44 = 20.
Поскольку потребность четвертого поставщика поставкой х44 = 20 полностью удовлетворена, то потребность обнуляется, а в остальных клетках четвертого столбца проставляется прочерк – в эти клетки другое поставки вноситься не будут.
У четвертого поставщика остается еще одна единица груза (21 – 20 = 1), которая подлежит дальнейшему распределению:
| bj ai | 1 | 2 | 3 | 4 | |
| 15/ | 16/ | 15/ | 20/0 | ||
| 1 | 14/ | 6 | 10 | | 5 - |
| 2 | 11/ | 10 | 7 | | 9 - |
| 3 | 20/5/ | 13 | 14 | | 7 - |
| 4 | 21/1/ | 5 | 10 - | 6 - | 4 20 |