Введем переменные: х₁ – объем производства продукции первого вида; х₂ – объем производства продукции второго вида; х₃ – объем производства продукции третьего вида.

Представим исходные данные в виде таблицы 11 - Исходные данные

Норма затрат Ресурсы		Виды изделий				Запас ресурсов		Скрытые цены ресурсов
					yi			yi*
		2	3	2	20
		6	4	3	40
		2	4	5	24
Цена единицы изделия		16	20	18	fmax(х)		gmin(у)
План выпуска	xj
	xj*

---

Целевая функция, отражающая доход от реализации произведенной продукции, представляет собой сумму произведений объема производства каждого вида продукции на значение ее цены:

,

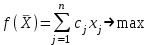где n – количество видов продукции.

Поскольку требуется максимизировать доход, то целевая функция стремиться к максимуму. При ресурсных ограничениях, представленных системой неравенств, левые части которых отражают затраты ресурсов каждого вида на производство продукции соответствующего вида, а правые отражают запасы ресурсов каждого вида. Знак неравенств «меньше или равно», поскольку расход ресурсов не должен превысить имеющихся запасов:

,

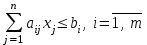где m – количество ресурсов.

Также должно выполняться условие не отрицательности переменных:

.

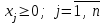Таким образом, экономико-математическая модель прямой задачи линейного программирования (ПЗЛП) варианта 0 имеет вид:



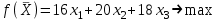
при ограничениях:



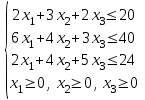
Данная ПЗЛП имеет стандартную форму записи, поскольку в задаче на максимум все функциональные (ресурсные) ограничения имеют знаки «меньше или равно».

2. Построение двойственной задачи к задаче распределения ресурсов

Для построения двойственной задачи линейного программирования (ДЗЛП) следует ввести двойственные переменные: у₁ – скрытая цена первого ресурса; у₂ – скрытая цена второго ресурса; у₃ – скрытая цена третьего ресурса.

Целевая функция ДЗЛП представляет собой совокупные затраты второго предприятия на приобретение всех ресурсов первого предприятия, при этом второе предприятие стремиться, чтобы его затраты на приобретение ресурсов у первого предприятия были минимальными:

.

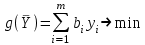Ограничениями ДЗЛП является система неравенств

---

, отражающая условия, при которых первому предприятию будет выгодно продать свои ресурсы вместо производства из них продукции, то есть при равенстве или превышении суммы, полученной от второго предприятия, над суммой дохода, полученной от реализации продукции:

.

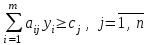Должно выполняться условие не отрицательности переменных:

.

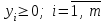Также для построения ДЗЛП можно руководствоваться следующими правилами.

1. В первой задаче определяется максимум линейной целевой функции, во второй – минимум.

2. Коэффициенты при переменных в целевой функции первой задачи являются правыми частями в системе ограничений во второй задаче.

3. Каждая из задач задана в стандартной форме, при этом в задаче максимизации все неравенства вида «меньше или равно», а в задаче минимизации все неравенства вида «больше или равно».

4. Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу. Для варианта 0 матрица коэффициентов при переменных в системе ограничений ПЗЛП имеет вид:



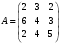
Тогда транспонированная матрица, отражающая коэффициенты при переменных в системе ограничений ДЗЛП, имеет вид:



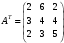
5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.

6. Условие не отрицательности переменных имеются в обеих задачах.

Таким образом, экономико-математическая модель ДЗЛП варианта 0 имеет вид:



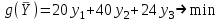
при ограничениях



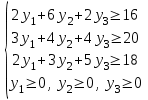
Данная ДЗЛП имеет стандартную форму записи, поскольку в задаче на минимум все функциональные (затратные) ограничения имеют знаки «больше или равно».
3. Решение прямой и двойственной задач линейного программирования

Для решения задачи линейного программирования необходимо перейти к ее канонической форме записи, то есть перейти в системе ограничений от функциональных неравенств к равенствам посредством включения дополнительных переменных.

---

Для ПЗЛП каноническая форма записи имеет вид:







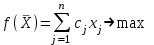
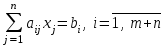
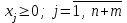
Для перехода к канонической форме записи ПЗЛП варианта 0 следует добавить дополнительные переменные х₄, х₅, х₆, в соответствующие неравенства со знаком «+», поскольку они отражают возможный остаток неиспользованных ресурсов:





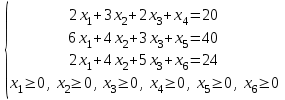
Для ДЗЛП каноническая форма записи имеет вид:







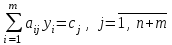
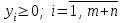
Для перехода к канонической форме записи ДЗЛП варианта 0 следует добавить дополнительные переменные y₄, y₅, y₆, в соответствующие неравенства со знаком «», поскольку они отражают возможное превышение затрат на приобретение ресурсов над ценой реализации продукции (возможный убыток от производства продукции):

---

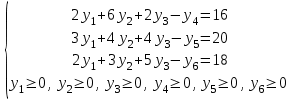
Соответствие переменных прямой и двойственной задачи

Во взаимно двойственных задачах линейного программирования первоначальным переменным ПЗЛП соответствуют дополнительные переменные ДЗЛП и аналогично первоначальным переменным ДЗЛП соответствуют дополнительные переменные ПЗЛП.

Установим соответствие переменных прямой и двойственной задачи для варианта 0:

х1 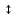y4

х2 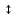y5

х3 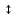y6

х4 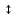y1

х5 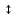y2

х6 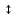у3

Решение задачи оптимального распределения ресурсов возможно двумя способами:

А. Одновременное решение ПЗЛП и ДЗЛП с помощью симплекс-таблиц.

Б. Двойственный симплекс-метод.

Рассмотрим оба метода.
А. Одновременное решение ПЗЛП и ДЗЛП с помощью симплекс-таблиц

Решаем ПЗЛП.

Находим исходное опорное решение и проверяем его на оптимальность. Для этого заполняем симплекс-таблицу. Все строки таблицы 1-го шага, за исключением строки _j (индексная строка), заполняем по данным системы ограничений и целевой функции канонической формы записи ПЗЛП.
Правила заполнения первой симплекс-таблицы

В первую строку с_j вносятся значения коэффициентов при переменных из целевой функции. В столбец базисных переменных вносим дополнительные переменные х_j.

В столбец с_i вносят значения коэффициентов при переменных из целевой функции, которые вошли в базис.

Рабочее поле таблицы (столбцы под переменными х_j заполняют коэффициентами при соответствующих переменных из системы равенств канонической формы записи ПЗЛП. Отсутствие той или иной переменной в равенстве означает, что ей

---

Смотрите также файлы

• Повышение конкурентоспособности организации на рынке гигиенических продуктов (на примере ооо Эссити).pdf

• Практических заданий по дисциплине жанры мультимедиа.docx

• Задачи представленной работы, способствующие достижению цели.docx

• 1. Данные, определенным образом организованные, имеющие смысл, значение и ценность для своего потребителя и необходимые для принятия им решений, а также реализации других функций и действий, это .docx

• Частное профессиональное образовательное учреждение Гуманитарный колледж Эдельвейс задание.docx