Заполняем столбцы для базисных переменных х₂, х₄, х₅:

сi	сj		16		20		18		0		0		0				min
	Базисные пере-менные (БП)		х1		х2		х3		х4		х5		х6		bi		bi/ hij
0	x4				0				1		0
0	x5				0				0		1
20	х2		1/2		1		5/4		0		0		1/4		6
j				0				0		0						-

Остальные клетки заполняем по правилу прямоугольника, отмечая, что ключевой элемент «4» находится в третьей строке и втором столбце предыдущей таблицы:

= ;

=

---

;

= ;

= ;

= ;

= ;

= ;

= .

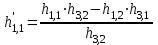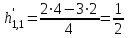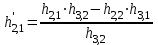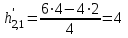
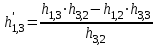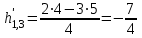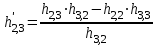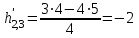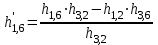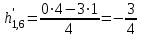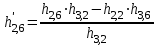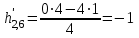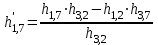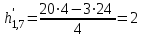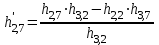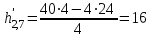сi	сj		16		20		18		0		0		0				min
	Базисные переменные (БП)		х1		х2		х3		х4		х5		х6		bi		bi/ hij
0	x4		1/2		0		-7/4		1		0		-3/4		2
0	x5		4		0		-2		0		1		-1		16
20	х2		1/2		1		5/4		0		0		1/4		6
j				0				0		0						-

---

Находим оценки переменных:

₁ = 0(1/2) + 04 + 20(1/2) – 16 = - 6;

₃ = 0(-7/4) + 0(-2) + 20(5/4) – 18 = 7;

₆ = 0(-3/4) + 0(-1) + 20(1/4) – 0 = 5; ₇= 02 + 016 + 206 = 120.

сi	сj		16		20		18		0		0		0				min
	Базисные переменные (БП)		х1		х2		х3		х4		х5		х6		bi		bi/ hij
0	x4		1/2		0		-7/4		1		0		-3/4		2
0	x5		4		0		-2		0		1		-1		16
20	х2		1/2		1		5/4		0		0		1/4		6
j		-6		0		7		0		0		5		120		-

---

Второе опорное решение имеет вид: 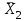= (0, 6, 0, 2, 16, 0), 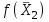= 120.

Однако это решение не оптимальное, поскольку оценка ₁ = - 6 <0.

Поскольку только одна оценка отрицательная, то выбираем этот столбец в качестве разрешающего. Следовательно, в базисные переводим переменную х₁.

сi	сj		16		20		18		0		0		0				min
	Базисные переменные (БП)		х1		х2		х3		х4		х5		х6		bi		bi/ hij
0	x4		1/2		0		-7/4		1		0		-3/4		2
0	x5		4		0		-2		0		1		-1		16
20	х2		1/2		1		5/4		0		0		1/4		6
j		-6		0		7		0		0		5		120		-

---

Для определения, того, какую переменную вывести из базисных, находим оценочные отношения:

сi	сj		16		20		18		0		0		0				min
	Базисные переменные (БП)		х1		х2		х3		х4		х5		х6		bi		bi/ hij
0	x4		1/2		0		-7/4		1		0		-3/4		2		2/(1/2)
0	x5		4		0		-2		0		1		-1		16		16/4
20	х2		1/2		1		5/4		0		0		1/4		6		6/(1/2)
j		-6		0		7		0		0		5		120		-

Минимальными являются два отношения в первой строке 2/(1/2) = 4 и во второй строке 16/4 = 4, поэтому в качестве разрешающей можно выбрать любую из них. Выбираем вторую строку, соответствующую переменной х₅, следовательно, переменная

---

Смотрите также файлы

• Повышение конкурентоспособности организации на рынке гигиенических продуктов (на примере ооо Эссити).pdf

• Практических заданий по дисциплине жанры мультимедиа.docx

• Задачи представленной работы, способствующие достижению цели.docx

• 1. Данные, определенным образом организованные, имеющие смысл, значение и ценность для своего потребителя и необходимые для принятия им решений, а также реализации других функций и действий, это .docx

• Частное профессиональное образовательное учреждение Гуманитарный колледж Эдельвейс задание.docx