Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Методы оптимальных решений.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 182
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
соответствует коэффициент, равный нулю.
В столбец bi вносят свободные члены системы равенств.
Индексная строка (j) для переменных находится по формуле:
,
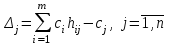где hij – соответствующий элемент, стоящий на пересечении i-й строки и j-го столбца рабочего поля симплекс таблицы.
Индексная строка (j) для свободного члена находится по формуле
,
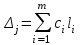где li – соответствующий элемент, из столбца bi.
В рассматриваемом варианте в первую строку сj вносим значения коэффициентов при переменных из целевой функции 16, 20 и 18, остальные значения равны нулю. В столбец базисных переменных вносим дополнительные переменные х4, х5, х6. В рассматриваемом случае базисные переменные не входят в целевую функцию, поэтому им соответствуют нулевые значения в столбце сi.
Рабочее поле таблицы (столбцы под переменными х1, х2, х3, х4, х5, х6) заполняем коэффициентами при соответствующих переменных из системы равенств канонической формы записи ПЗЛП.
Поскольку, в первом равенстве отсутствуют переменные х5 и х6, поэтому в первой рабочей строке симплекс-таблицы этим переменным соответствует коэффициент «0».
Заполняем индексную строку:
1 = 02 + 06 + 02 – 16 = -16;
2 = 03 + 04 + 04 – 20 = -20;
3 = 02 + 03 + 05 – 18 = -18;
4 = 0; 5 = 0; 6 = 0;
7= 020 + 040 + 024 = 0.
Первое опорное решение имеет вид:
= (0, 0, 0, 20, 40, 24), 
= 0. (компоненты опорного решения выписывают для базисных переменных из столбца свободных членов bi; переменные, не входящие в базис, имеют значение 0). В рассматриваемом случае переменные х1, х2, х3. не входят в базис, поэтому их компоненты в опорном решении равны нулю, базисные переменные имеют значения х4= 20, х5 = 40, х6 = 24. Значение целевой функции берут из последней строки столбца 
. На данном шаге симплекс-метода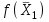
= 0.
Следует проверить первое опорное решение на оптимальность.
Проверка первого опорного решения на оптимальность
Возможны следующие случаи решения задачи на максимум:
- если все оценки j 0, то найденное решение оптимальное;
- если хотя бы одна оценка j 0, но при соответствующей переменной нет ни одного положительного коэффициента, решение задачи прекращают, так как f(X) , т.е. целевая функция не ограничена в области допустимых решений;
- если хотя бы одна оценка отрицательная, а при соответствующей переменной есть хотя бы один положительный коэффициент, то нужно перейти к другому опорному решению;
- если отрицательных оценок в индексной строке несколько, то в столбец базисной переменной (БП) вводят ту переменную, которой соответствует наибольшая по абсолютной величине отрицательная оценка.
В рассматриваемом случае первое опорное решение не оптимальное, поскольку имеются три отрицательные оценки 1 = - 16, 2 = - 20, 3 = - 18.
Следовательно, нужно сделать следующий шаг симплекс-метода: ввести в базис переменную, которую нужно улучшить.
Правило выбора переменной для введения в базисные переменные
(правило выбора ключевого, или разрешающего, столбца)
Пусть одна оценка k 0 или наибольшая по абсолютной величине k 0, тогда k-й столбец принимают за ключевой (разрешающий).
Такой переменной является переменная из столбца с наибольшей по абсолютной величине оценкой 2 = 20, т.е. переменная х2.
Теперь следует определить, какую переменную нужно вывести из базиса.
Правило выбора переменной для вывода из базисных переменных
(правило выбора ключевой (разрешающей) строки
За ключевую (разрешающую) строку принимают ту, которой соответствует минимальное отношение свободных членов (bi) к положительным коэффициентам ключевого k-го столбца. Элемент, находящийся на пересечении ключевых строки и столбца, называют ключевым (разрешающим) элементом.
В столбце оценочных отношений min{bi/hij} отражены отношения свободных членов к элементам из разрешающего столбца, минимальным является отношение 24/4, соответствующее строке переменной х6, следовательно, эта строка – разрешающая, а переменная х6 выводится из базисных переменных:
На пересечении ключевой строки и ключевого столбца находится ключевой элемент «4».
Переход ко второму шагу симплекс-метода.
Правила заполнения следующей таблицы симплекс-метода
В столбец базисных переменных на место выведенной из базисных вносится новая базисная переменная. При этом в столбец сi вносится соответствующее значение коэффициента при переменной из целевой функции.
Ключевая строка переписывается, при этом все ее элементы делят на ключевой элемент.
Заполняют столбцы для базисных переменных: на пересечении строки и столбца, в которых находится одна и та же переменная, ставят «1», в остальных клетках столбца нули.
Остальные коэффициенты таблицы находят по правилу «прямоугольника»: для искомого элемента новой таблицы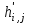
выбирают стоящий на пересечении той же строки и того же столбца элемент из предыдущей таблицы 
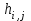, умножают его на разрешающий 
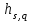, из этого произведения вычитают произведение элементов, расположенных на противоположной диагонали прямоугольника, образуемого искомым и разрешающим элементами, а полученную разность делят на разрешающий элемент 
.
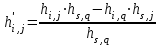Оценки j можно считать по приведенным ранее формулам или по правилу «прямоугольника».
Заполним симплекс-таблицу второго шага для варианта 0. Вместо переменной х6 вводим в базис переменную х2, в целевой функции ей соответствует коэффициент 20, который вносится в соответствующую клетку столбца сi.
В строке, соответствующей переменной х2 переписываем элементы из ключевой строки предыдущей таблицы, предварительно разделив их на ключевой элемент «4»:
В столбец bi вносят свободные члены системы равенств.
Индексная строка (j) для переменных находится по формуле:
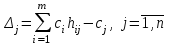, где hij – соответствующий элемент, стоящий на пересечении i-й строки и j-го столбца рабочего поля симплекс таблицы.
Индексная строка (j) для свободного члена находится по формуле
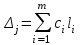,где li – соответствующий элемент, из столбца bi.
В рассматриваемом варианте в первую строку сj вносим значения коэффициентов при переменных из целевой функции 16, 20 и 18, остальные значения равны нулю. В столбец базисных переменных вносим дополнительные переменные х4, х5, х6. В рассматриваемом случае базисные переменные не входят в целевую функцию, поэтому им соответствуют нулевые значения в столбце сi.
Рабочее поле таблицы (столбцы под переменными х1, х2, х3, х4, х5, х6) заполняем коэффициентами при соответствующих переменных из системы равенств канонической формы записи ПЗЛП.
Поскольку, в первом равенстве отсутствуют переменные х5 и х6, поэтому в первой рабочей строке симплекс-таблицы этим переменным соответствует коэффициент «0».
| сi | сj | 16 | 20 | 18 | 0 | 0 | 0 |  |
| Базисные переменные (БП) | х1 | х2 | х3 | х4 | х5 | х6 | bi | |
| 0 | x4 | 2 | 3 | 2 | 1 | 0 | 0 | 20 |
| 0 | x5 | 6 | 4 | 3 | 0 | 1 | 0 | 40 |
| 0 | х6 | 2 | 4 | 5 | 0 | 0 | 1 | 24 |
| j | | | | | | | | |
Заполняем индексную строку:
1 = 02 + 06 + 02 – 16 = -16;
2 = 03 + 04 + 04 – 20 = -20;
3 = 02 + 03 + 05 – 18 = -18;
4 = 0; 5 = 0; 6 = 0;
7= 020 + 040 + 024 = 0.
| сi | сj | 16 | 20 | 18 | 0 | 0 | 0 | |
| Базисные переменные (БП) | х1 | х2 | х3 | х4 | х5 | х6 | bi | |
| 0 | x4 | 2 | 3 | 2 | 1 | 0 | 0 | 20 |
| 0 | x5 | 6 | 4 | 3 | 0 | 1 | 0 | 40 |
| 0 | х6 | 2 | 4 | 5 | 0 | 0 | 1 | 24 |
| j | -16 | -20 | -18 | 0 | 0 | 0 | 0 | |
Первое опорное решение имеет вид:
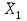= (0, 0, 0, 20, 40, 24), 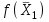= 0. (компоненты опорного решения выписывают для базисных переменных из столбца свободных членов bi; переменные, не входящие в базис, имеют значение 0). В рассматриваемом случае переменные х1, х2, х3. не входят в базис, поэтому их компоненты в опорном решении равны нулю, базисные переменные имеют значения х4= 20, х5 = 40, х6 = 24. Значение целевой функции берут из последней строки столбца . На данном шаге симплекс-метода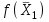
= 0.
Следует проверить первое опорное решение на оптимальность.
Проверка первого опорного решения на оптимальность
Возможны следующие случаи решения задачи на максимум:
- если все оценки j 0, то найденное решение оптимальное;
- если хотя бы одна оценка j 0, но при соответствующей переменной нет ни одного положительного коэффициента, решение задачи прекращают, так как f(X) , т.е. целевая функция не ограничена в области допустимых решений;
- если хотя бы одна оценка отрицательная, а при соответствующей переменной есть хотя бы один положительный коэффициент, то нужно перейти к другому опорному решению;
- если отрицательных оценок в индексной строке несколько, то в столбец базисной переменной (БП) вводят ту переменную, которой соответствует наибольшая по абсолютной величине отрицательная оценка.
В рассматриваемом случае первое опорное решение не оптимальное, поскольку имеются три отрицательные оценки 1 = - 16, 2 = - 20, 3 = - 18.
Следовательно, нужно сделать следующий шаг симплекс-метода: ввести в базис переменную, которую нужно улучшить.
Правило выбора переменной для введения в базисные переменные
(правило выбора ключевого, или разрешающего, столбца)
Пусть одна оценка k 0 или наибольшая по абсолютной величине k 0, тогда k-й столбец принимают за ключевой (разрешающий).
Такой переменной является переменная из столбца с наибольшей по абсолютной величине оценкой 2 = 20, т.е. переменная х2.
| сi | сj | 16 | 20 | 18 | 0 | 0 | 0 | | min | ||||||||
| Базисные переменные (БП) | х1 | х2 | х3 | х4 | х5 | х6 | bi | bi/ hij | |||||||||
| 0 | x4 | 2 | 3 | 2 | 1 | 0 | 0 | 20 | | ||||||||
| 0 | x5 | 6 | 4 | 3 | 0 | 1 | 0 | 40 | | ||||||||
| 0 | х6 | 2 | 4 | 5 | 0 | 0 | 1 | 24 | | ||||||||
| j | -16 | -20 | -18 | 0 | 0 | 0 | 0 | | |||||||||
Теперь следует определить, какую переменную нужно вывести из базиса.
Правило выбора переменной для вывода из базисных переменных
(правило выбора ключевой (разрешающей) строки
За ключевую (разрешающую) строку принимают ту, которой соответствует минимальное отношение свободных членов (bi) к положительным коэффициентам ключевого k-го столбца. Элемент, находящийся на пересечении ключевых строки и столбца, называют ключевым (разрешающим) элементом.
В столбце оценочных отношений min{bi/hij} отражены отношения свободных членов к элементам из разрешающего столбца, минимальным является отношение 24/4, соответствующее строке переменной х6, следовательно, эта строка – разрешающая, а переменная х6 выводится из базисных переменных:
| сi | сj | 16 | 20 | 18 | 0 | 0 | 0 | | min | ||||||||
| Базисные переменные (БП) | х1 | х2 | х3 | х4 | х5 | х6 | bi | bi/ hij | |||||||||
| 0 | x4 | 2 | 3 | 2 | 1 | 0 | 0 | 20 | 20/3 | ||||||||
| 0 | x5 | 6 | 4 | 3 | 0 | 1 | 0 | 40 | 40/4 | ||||||||
| 0 | х6 | 2 | «4» | 5 | 0 | 0 | 1 | 24 | 24/4 | ||||||||
| j | -16 | -20 | -18 | 0 | 0 | 0 | 0 | - | |||||||||
На пересечении ключевой строки и ключевого столбца находится ключевой элемент «4».
Переход ко второму шагу симплекс-метода.
Правила заполнения следующей таблицы симплекс-метода
В столбец базисных переменных на место выведенной из базисных вносится новая базисная переменная. При этом в столбец сi вносится соответствующее значение коэффициента при переменной из целевой функции.
Ключевая строка переписывается, при этом все ее элементы делят на ключевой элемент.
Заполняют столбцы для базисных переменных: на пересечении строки и столбца, в которых находится одна и та же переменная, ставят «1», в остальных клетках столбца нули.
Остальные коэффициенты таблицы находят по правилу «прямоугольника»: для искомого элемента новой таблицы
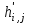выбирают стоящий на пересечении той же строки и того же столбца элемент из предыдущей таблицы 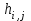, умножают его на разрешающий 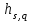, из этого произведения вычитают произведение элементов, расположенных на противоположной диагонали прямоугольника, образуемого искомым и разрешающим элементами, а полученную разность делят на разрешающий элемент 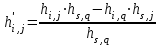.Оценки j можно считать по приведенным ранее формулам или по правилу «прямоугольника».
Заполним симплекс-таблицу второго шага для варианта 0. Вместо переменной х6 вводим в базис переменную х2, в целевой функции ей соответствует коэффициент 20, который вносится в соответствующую клетку столбца сi.
В строке, соответствующей переменной х2 переписываем элементы из ключевой строки предыдущей таблицы, предварительно разделив их на ключевой элемент «4»:
| сi | сj | 16 | 20 | 18 | 0 | 0 | 0 | | min |
| Базисные пере-менные (БП) | х1 | х2 | х3 | х4 | х5 | х6 | bi | bi/ hij | |
| 0 | x4 | | | | | | | | |
| 0 | x5 | | | | | | | | |
| 20 | х2 | 1/2 | 1 | 5/4 | 0 | 0 | 1/4 | 6 | |
| j | | | | | | | | - | |