Файл: Дидактическая игра как средство активизации познавательной деятельности младших школьников на факультативе изучаем мир, играя.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 198
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Математическая обработка данных
Гипотезы:
H0: Интенсивность сдвигов в сторону уменьшения показателя не превышает интенсивности сдвигов в сторону ее увеличения.
H1: Интенсивность сдвигов в сторону уменьшения показателя превышает интенсивность сдвигов в сторону ее увеличения.
Сумма по столбцу рангов равна ∑=300
Проверка правильности составления матрицы на основе исчисления контрольной суммы:
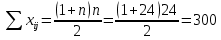
Сумма по столбцу и контрольная сумма равны между собой, значит, ранжирование проведено правильно.
Теперь отметим те сдвиги, которые являются нетипичными, в данном случае - положительными. В таблице эти сдвиги и соответствующие им ранги выделяются курсивом.
Сумма рангов этих «редких» сдвигов составляет эмпирическое значение критерия Т: T=∑Rt=0
По таблице Приложения находим критические значения для Т-критерия Вилкоксона для n=24:
Tкр= 69(p≤0.01)
Tкр= 91(p≤0.05)
Зона значимости в данном случае простирается влево, действительно, если бы «редких», в данном случае положительных, сдвигов не было совсем, то и сумма их рангов равнялась бы нулю.
В данном же случае эмпирическое значение Т попадает в зону незначимости: Тэмп<Ткр(0,01).
Гипотеза H0 принимается. Показатели после эксперимента превышают значения показателей до опыта.
ПРИЛОЖЕНИЕ 13
Результаты повторной диагностики по методике, направленной на определение познавательной самостоятельности младших школьников. «Познавательная самостоятельность младшего школьника» по А. А. Горчинской (в адаптации) и статистическая обработка данных по Т-критерию Вилкоксона
Математическая обработка данных
Гипотезы:
H0: Интенсивность сдвигов в сторону уменьшения показателя не превышает интенсивности сдвигов в сторону ее увеличения.
H1: Интенсивность сдвигов в сторону уменьшения показателя превышает интенсивность сдвигов в сторону ее увеличения.
Сумма по столбцу рангов равна ∑=300
Проверка правильности составления матрицы на основе исчисления контрольной суммы:

Сумма по столбцу и контрольная сумма равны между собой, значит, ранжирование проведено правильно.
Теперь отметим те сдвиги, которые являются нетипичными, в данном случае - положительными. В таблице эти сдвиги и соответствующие им ранги выделяются курсивом.
Сумма рангов этих «редких» сдвигов составляет эмпирическое значение критерия Т: T=∑Rt=0
По таблице Приложения находим критические значения для Т-критерия Вилкоксона для n=24:
Tкр= (p≤0.01)
Tкр= (p≤0.05)
Зона значимости в данном случае простирается влево, действительно, если бы «редких», в данном случае положительных, сдвигов не было совсем, то и сумма их рангов равнялась бы нулю.
В данном же случае эмпирическое значение Т попадает в зону незначимости: Тэмп<Ткр(0,01).
Гипотеза H0 принимается. Показатели после эксперимента превышают значения показателей до опыта.
Гипотезы:
H0: Интенсивность сдвигов в сторону уменьшения показателя не превышает интенсивности сдвигов в сторону ее увеличения.
H1: Интенсивность сдвигов в сторону уменьшения показателя превышает интенсивность сдвигов в сторону ее увеличения.
| № | Результат до эксперимента | Результат после эксперимента | Разность (tдо-tпосле) | Абсолютное значение разности | Ранговый номер разности | |
| 1 | 61 | 63 | 2 | 2 | 3 | |
| 2 | 46 | 51 | 5 | 5 | 14 | |
| 3 | 36 | 45 | 9 | 9 | 22,5 | |
| 4 | 45 | 47 | 2 | 2 | 3 | |
| 5 | 41 | 44 | 3 | 3 | 7,5 | |
| 6 | 42 | 48 | 6 | 6 | 16,5 | |
| 7 | 48 | 54 | 6 | 6 | 16,5 | |
| 8 | 39 | 42 | 3 | 3 | 7,5 | |
| 9 | 44 | 53 | 9 | 9 | 22,5 | |
| 10 | 59 | 62 | 4 | 4 | 11 | |
| 11 | 59 | 61 | 2 | 2 | 3 | |
| 12 | 31 | 38 | 7 | 7 | 19 | |
| 13 | 46 | 51 | 5 | 5 | 14 | |
| 14 | 31 | 40 | 9 | 9 | 22,5 | |
| 15 | 43 | 47 | 4 | 4 | 11 | |
| 16 | 25 | 32 | 7 | 7 | 19 | |
| 17 | 36 | 45 | 9 | 9 | 22,5 | |
| 18 | 64 | 66 | 2 | 2 | 3 | |
| 19 | 61 | 64 | 3 | 3 | 7,5 | |
| 20 | 41 | 44 | 3 | 3 | 7,5 | |
| 21 | 40 | 47 | 7 | 7 | 19 | |
| 22 | 59 | 64 | 5 | 5 | 14 | |
| 23 | 60 | 62 | 2 | 2 | 3 | |
| 24 | 42 | 46 | 4 | 4 | 11 | |
| Сумма по столбцу рангов | 300 | |||||
| Сумма рангов нетипичных сдвигов | TЭмп = 0 | |||||
Сумма по столбцу рангов равна ∑=300
Проверка правильности составления матрицы на основе исчисления контрольной суммы:
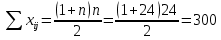
Сумма по столбцу и контрольная сумма равны между собой, значит, ранжирование проведено правильно.
Теперь отметим те сдвиги, которые являются нетипичными, в данном случае - положительными. В таблице эти сдвиги и соответствующие им ранги выделяются курсивом.
Сумма рангов этих «редких» сдвигов составляет эмпирическое значение критерия Т: T=∑Rt=0
По таблице Приложения находим критические значения для Т-критерия Вилкоксона для n=24:
Tкр= 69(p≤0.01)
Tкр= 91(p≤0.05)
| n | TКр | |
| p<0,05 | p<0,01 | |
| 24 | 91 | 69 |
Зона значимости в данном случае простирается влево, действительно, если бы «редких», в данном случае положительных, сдвигов не было совсем, то и сумма их рангов равнялась бы нулю.
В данном же случае эмпирическое значение Т попадает в зону незначимости: Тэмп<Ткр(0,01).
Гипотеза H0 принимается. Показатели после эксперимента превышают значения показателей до опыта.
ПРИЛОЖЕНИЕ 13
Результаты повторной диагностики по методике, направленной на определение познавательной самостоятельности младших школьников. «Познавательная самостоятельность младшего школьника» по А. А. Горчинской (в адаптации) и статистическая обработка данных по Т-критерию Вилкоксона
| № | Ф.И.О. ученика | Познавательная самостоятельность младшего школьника | |||
| До проведения программы | После проведения программы | ||||
| Большинство вариантов ответа | Уровень самостоятельности | Большинство вариантов ответа | Уровень самостоятельности | ||
| 1 | Элина Б.И. | 9 | высокий | 11 | высокий |
| 2 | Ярослав Б.А | 11 | высокий | 12 | высокий |
| 3 | Кирилл В.Р. | 5 | средний | 8 | высокий |
| 4 | Ксения В.В. | 8 | высокий | 10 | высокий |
| 5 | Злата В.М. | 9 | высокий | 12 | высокий |
| 6 | Дарья В.В. | 6 | средний | 9 | высокий |
| 7 | Артем Г.А. | 8 | высокий | 11 | высокий |
| 8 | Владимир Г.В. | 4 | средний | 7 | высокий |
| 9 | Алексей Д.И. | 4 | средний | 8 | средний |
| 10 | Варвара Д.Р. | 9 | высокий | 11 | высокий |
| 11 | Злата З.О. | 11 | высокий | 11 | высокий |
| 12 | Юлия Л.В. | 6 | средний | 8 | высокий |
| 13 | Дмитрий Н.И. | 8 | высокий | 9 | высокий |
| 14 | Арсений О.М. | 2 | низкий | 5 | средний |
| 15 | София О.Р. | 4 | средний | 7 | высокий |
| 16 | Анна П.А. | 1 | низкий | 4 | средний |
| 17 | София П.П. | 10 | высокий | 12 | высокий |
| 18 | Елизавета П.М. | 9 | высокий | 11 | высокий |
| 19 | Аделина П.Н. | 8 | высокий | 9 | высокий |
| 20 | Вера Р.В. | 6 | средний | 6 | средний |
| 21 | Таисия С.М. | 5 | средний | 6 | средний |
| 22 | Сергей Т.В. | 9 | высокий | 11 | высокий |
| 23 | Даниил Ф.В. | 4 | средний | 7 | высокий |
| 24 | Ярослав Х.Д. | 6 | средний | 9 | высокий |
| № | Уровень познавательной активности | Количество учеников | |
| До проведения программы | После проведения программы | ||
| 1 | Высокий уровень познавательной активности (большинство ответов «а») | 12 | 19 |
| 2 | Средний уровень познавательной активности (большинство ответов «б») | 10 | 5 |
| 3 | Низкий уровень познавательной активности (большинство ответов «в») | 2 | 0 |
Математическая обработка данных
Гипотезы:
H0: Интенсивность сдвигов в сторону уменьшения показателя не превышает интенсивности сдвигов в сторону ее увеличения.
H1: Интенсивность сдвигов в сторону уменьшения показателя превышает интенсивность сдвигов в сторону ее увеличения.
| № | Результат до эксперимента | Результат после эксперимента | Разность (tдо-tпосле) | Абсолютное значение разности | Ранговый номер разности | |
| 1 | 9 | 11 | 2 | 2 | 10 | |
| 2 | 11 | 12 | 1 | 1 | 4.5 | |
| 3 | 5 | 8 | 3 | 3 | 18.5 | |
| 4 | 8 | 10 | 2 | 2 | 10 | |
| 5 | 9 | 12 | 3 | 3 | 18.5 | |
| 6 | 6 | 9 | 3 | 3 | 18.5 | |
| 7 | 8 | 11 | 3 | 3 | 18.5 | |
| 8 | 4 | 7 | 3 | 3 | 18.5 | |
| 9 | 4 | 8 | 4 | 4 | 24 | |
| 10 | 9 | 11 | 2 | 2 | 10 | |
| 11 | 11 | 11 | 0 | 0 | 1.5 | |
| 12 | 6 | 8 | 2 | 2 | 10 | |
| 13 | 8 | 9 | 1 | 1 | 4.5 | |
| 14 | 2 | 5 | 3 | 3 | 18.5 | |
| 15 | 4 | 7 | 3 | 3 | 18.5 | |
| 16 | 1 | 4 | 3 | 3 | 18.5 | |
| 17 | 10 | 12 | 2 | 2 | 10 | |
| 18 | 9 | 11 | 2 | 2 | 10 | |
| 19 | 8 | 9 | 1 | 1 | 4.5 | |
| 20 | 6 | 6 | 0 | 0 | 1.5 | |
| 21 | 5 | 6 | 1 | 1 | 4.5 | |
| 22 | 9 | 11 | 2 | 2 | 10 | |
| 23 | 4 | 7 | 3 | 3 | 18.5 | |
| 24 | 6 | 9 | 3 | 3 | 18.5 | |
| Сумма по столбцу рангов | 300 | |||||
| Сумма рангов нетипичных сдвигов | TЭмп = 0 | |||||
Сумма по столбцу рангов равна ∑=300
Проверка правильности составления матрицы на основе исчисления контрольной суммы:

Сумма по столбцу и контрольная сумма равны между собой, значит, ранжирование проведено правильно.
Теперь отметим те сдвиги, которые являются нетипичными, в данном случае - положительными. В таблице эти сдвиги и соответствующие им ранги выделяются курсивом.
Сумма рангов этих «редких» сдвигов составляет эмпирическое значение критерия Т: T=∑Rt=0
По таблице Приложения находим критические значения для Т-критерия Вилкоксона для n=24:
Tкр= (p≤0.01)
Tкр= (p≤0.05)
| n | TКр | |
| p<0,05 | p<0,01 | |
| 3 | 91 | 69 |
Зона значимости в данном случае простирается влево, действительно, если бы «редких», в данном случае положительных, сдвигов не было совсем, то и сумма их рангов равнялась бы нулю.
В данном же случае эмпирическое значение Т попадает в зону незначимости: Тэмп<Ткр(0,01).
Гипотеза H0 принимается. Показатели после эксперимента превышают значения показателей до опыта.